Моделирование процессов охлаждения и формирования твердости экструдата

Введение. Экструзионные технологии переработки растительного сырья, позволяющие изменить в широком диапазоне свойства готового продукта, нашли широкое распространение при производстве продуктов питания [1–6].

Одним из показателей структуры экструдата является его твердость, которая зависит от влажности исходного сырья, температуры и частоты вращения шнека экструдера. Увеличение содержания в растительном сырье протеина и пищевых волокон, повышение влажности сырья с 12 до 17 % повышает твердость экструдата [1].

В связи с этим теоретические исследования с использованием аналитического аппарата [7], направленные на выявление закономерности изменения температуры экструдата, моделирование и прогнозирование поведения системы охлаждения и формирования твердости экструдата является актуальной задачей.

Цель исследования – раскрыть закономерности процессов охлаждения и формирования твердости экструдата в технологической линии получения текстурированной муки.

Задачи: выявить причинно-следственные связи и определить результатные и факторные показатели охлаждения и формирования твердости экструдата; разработать теоретические и расчетные схемы определения состояния исследуемой системы и получить модельное представление ее результатных показателей.

Материалы и методы. В работе использованы методы математического моделирования, организации и планирования эксперимента, аппарат дескриптивной статистики, корреляционнорегрессионного анализа, теории случайных процессов, статистические тесты Пирсона, Стьюдента и Дарбина - Ватсона, а также методы математического анализа, реализованные в компьютерном пакете Statistics системы Maple.

Учеными Красноярского ГАУ была разработана и запатентована конструкция охладителя экструдата [8]. Разработан план опытов и выполнено экспериментальное исследование технологической линии с включенным охладителем, обладающим новыми конструктивными, режимными и технологическими характеристиками. Предварительный анализ системы охлаждения и формирования твердости экструдата выявил факторные и результатные показатели данной системы, позволил получить числовые оценки статистических характеристик.

Факторные показатели исследуемой системы определяют технико-технологические условия процессов охлаждения и формирования твердости экструдата. Так, показатель температуры агента охлаждения ( х 1 , °C) варьируется в диапазоне –29…20 °C, имеет среднее значение 1,1250 °C и стандартное отклонение 18,7588 °C.

Показатель продолжительности процесса охлаждения ( х 1 , мин) варьируется в диапазоне 00…20 мин, имеет среднее значение 10 мин и стандартное отклонение 7,2548 мин.

Результатные показатели системы «охлаждения и формирования твердости экструдата» описывают динамику сопряженных процессов охлаждения и формирования твердости экструдата. Так, показатель формируемой твердости экструдата в процессе его охлаждения ( у 1 , кг/см²) варьируется в диапазоне 0,20^17,21 кг/см², имеет среднее значение 9,8170 кг/см² при стандартном отклонении 5,5968 кг/см².

Показатель температуры, изменяющейся в процессе охлаждения экструдата ( у 2 , °C) варьируется в диапазоне 13,90…72,70 °C, имеет среднее значение 37,6600 °C при стандартном отклонении 19,8200 °C.

Для исследования тесноты связи (силы взаимодействия) группы факторных показателей с группой результатных показателей системы охлаждения и формирования твердости экструдата вычисляют и анализируют коэффициенты корреляции ^ ij .

Факторные показатели температуры агента охлаждения ( х 1 , °C) и продолжительности процесса охлаждения ( х 2 , мин) не коррелированы, поскольку их коэффициент корреляции равен нулю, р ( X j, x ₂) = 0 . Однако, результатные показатели формируемой твердости экструдата в процессе его охлаждения ( у 1 , кг/см²) и температуры, изменяющейся в процессе охлаждения экструдата ( у 2 , °C) сильно коррелированы, поскольку их парный коэффициент корреляции р ( У 1, У 2 ) = - 0.9007 достаточно близок к -1. На оба результатных показателя в большее влияние оказывает фактор продолжительности процесса охлаждения ( х 2 , мин) и меньшее влияние оказывает фактор температуры агента охлаждения ( х 1 , °C), так как, соответственно, р ( x ₂, у ) = 0.8958 , р ( x ₂, у ₂) =- 0.8863 и р ( x , у ) = 0.2286 , р ( у , у ₂) = 0.1495 .

Рассмотрим физическую интерпретацию отыскиваемой функции у = f ( х 1 , х 2 ) как закономерности изменения температуры остывающего тела (и любого подобного процесса). Тогда в начальный момент времени температура будет максимальна, скажем, α °C, а при неограниченном продолжении процесса охлаждения, температура тела будет стремиться к температуре агента охлаждения, то есть х 1 °C:

f ( x j , 0 ) = а , f ( x j , +® ) = у .

Условиям интерпретации удовлетворяет, например, функция двух переменных х 1 , х 2 и с двумя параметрами а , к :

f ( у , x ₂) = у + ( а - x ) ■ exp ( k • x ₂) , при k < 0.

Очевидно, что по условиям подойдет любая функция двух переменных х 1 , х 2 с несколькими параметрами:

f (Х[, x2) = x +(a-Xj + G(Xj, x2))• exp(k• x2), если потребовать G(хi, 0) = 0 и G(хi, х2)) • exp (k • х2) ^ 0 при х2 ^ +x.

Формирование твердости экструдата ( у i , кг/см²) в зависимости от температуры агента охлаждения ( х 1 , °C) и продолжительности процесса охлаждения ( х 2 , мин) на уровне детерминации 98,21 % представляется следующей квазиполиномиальной функцией 3-й степени (рис. 1):

X — f ( X j , x₂ ) — x + ( a - x + L ( X i , x₂ ) + Q ( X i , X 2 ) + H ( X , x₂ ) ) • exp ( k • x₂ ) , где L ( x , x ₂) — b ₂ • x ₂,

Q ( x i , X ₂ ) = b i, • x i x ₂ + b 22 • x 2 ^,

H (xi, x2 ) — bii2 • xi x2 + Ь^2 • X1 X2 + b222 • X2 + b1222 • X1 X2 , соответственно линейная, квадратичная и кубическая формы, составляющие регрессионную функцию;

a — 0.20, k — -0.0925644109, b2 — 4.0720676127, b2 —-0.0745071886, b22 —-0.2854098946, bn2 —-0.0005008694, b2 2 — 0.0045441568, b222 — 0.0168806379, bi222 —-0.0001872144, соответственно коэффициенты регрессии, отыскиваемые методом наименьших квадратов с помощью компьютерного пакета, причем все коэффициенты оказались значимыми в соответствии с критерием (статистическим тестом) Стьюдента (Госсета).

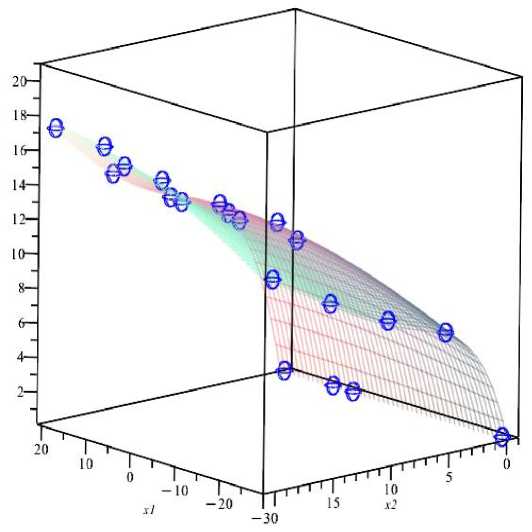
Рис. 1. Изменение формируемой твердости экструдата (у 1 , ч) при изменениях температуры агента охлаждения (х 1 , °C) и продолжительности процесса охлаждения (х 2 , мин)

Change in the formed hardness of the extrudate (y 1 , h) with changes in the temperature of the cooling agent (x i , °C) and the duration of the cooling process (x 2 , min)

Относительная погрешность приближения не превосходит 3,10 %, а среднее отклонений оценивается числом близким к нулю –0,0001, средние значения фактической и вычисленной твердости экструдата, соответственно 9,8170 и 9,8169 кг/см2 в пределах принятой точности вычислений также неразличимы, что указывает на точность и практически несмещенность оценок, получаемых с помощью предложенной схемы.

Изменение температуры экструдата ( у 2 , °C ) в зависимости от температуры агента охлаждения ( х i , °C ) и продолжительности процесса охлаждения ( х 2 , мин ) на уровне детерминации 96,78 % представляется указанной выше квазиполиномиальной функцией 3-й степени, но с другими значениями коэффициентов (рис. 2):

У2 = f (x1, x2 ) , f (Xj, x2) = x + (a-x + G(x, x2))‘exp(k•x2),

G ( x , x ₂) = b ₂ • x ₂ + b ₁₂ • x x ₂ + b₂₂

■ x ₂ + b ₁₁₂ • x j x ₂ + b j22 ' ^x i ^x 2 ^{+ b} 222 • x 2 ^{+ b} 1222 ’ x 1 x 2 ,

a = 72.70, k = -0.1723491527, b2 =-5.1043465808 , b12 =-0.0279429733, b22 = 0.9873802564, bn2 = 0.0104942473 , b122 = 0.0152034351, b222 = 0.0188655998 , b1222 = -0.0033325720, которые также являются значимыми в соответствии с критерием (статистическим тестом) Стьюдента.

Стало быть, предложенная формула распространяет на область пищевых систем известный эмпирический закон остывания нагретых тел описанный Ньютоном:

f ( x , x ₂) = x + ( a - x ) • exp ( k • x ₂) .

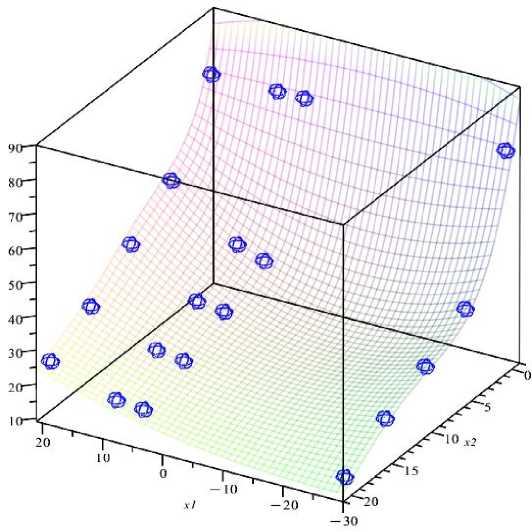
Рис. 2. Изменение температуры экструдата (у 2 , °C) при изменениях температуры агента охлаждения (х 1 , °C) и продолжительности процесса охлаждения (х 2 , мин)

Change in the temperature of the extrudate (y 2 , °C) with changes in the temperature of the cooling agent (x 1 , °C) and the duration of the cooling process (x 2 , min)

Относительная погрешность приближения не превосходит 4,40 %, а среднее отклонений оценивается –0,0017 °C. Средние значения факти- ческой и вычисленной температуры, соответст венно, 37,6600 и 37,6583 °C в пределах приня той точности вычислений практически не разли чимы. Поэтому оценки, получаемые с помощью предложенной схемы и в пределах принятой точности, можно считать практически несмещенными.

Заключение. Выявленные закономерности изменения твердости и температуры экструдата в процессе его охлаждения обобщают известный эмпирический закон Ньютона, распространяющийся на объекты системы охлаждения и формирования твердости экструдата, и поэтому она может быть использована для прогнозирования трансформации пищевого сырья с высокой точностью.

Предложены теоретические и расчетные схемы определения состояния исследуемой системы охлаждения и формирования твердости экструдата, а также получены модельные представления высокой точности для прогнозирования значений результатных показателей и сопряженных биофизических свойств полуфабриката.