Моделирование процессов термовлагомеханики при сушке риса

Термовлагомеханика перспективное научное направление анализа процесса сушки зерновых материалов, обосновывающее структурное поведение объекта сушки в зависимости от режимов процесса. Развитие деформаций и прочностные свойства материалов находятся в сфере внимания прикладной механики. Зерно риса обязательно подвергается сушке и имеющая место при этом трещиноватость определяет ценность получаемого продукта.

Кинетические зависимости процесса сушки, т.е. описание во времени изменения основных параметров, имеют большое практическое значение для управления процессом, определения режимов обеспечивающих качество продукта и энергетических затрат на проведение данного процесса. При этом качество получаемых кинетических зависимостей определяется правильным определением механизма процесса и применением соответствующих математических моделей [1].

Важными являются не только зависимо-

сти изменения влажности материала при сушке, но и температурные зависимости нагрева высушиваемого материала. Фундаментальной работой в области теории сушки является обоснование [2] системы дифференциальных уравнений, описывающих изменения влагосодержа-ния, температуры и давления. Сложность решения этой системы затрудняет ее практическое использование [3]. Сделана попытка [4] описать

Систему в дифференциальной форме можно преобразовать к нормальной форме избавившись от m s в левой части уравнений.

dX (T ) = Am ' hm . Лф aB ' Pw" [T (T )] | dT         ms      [ Фа ' Pw" (Ta ) J                 (6)

кинетику процесса сушки на основе перехода к потенциалам массопереноса.

Упрощением является переход [5] к системе обыкновенных дифференциальных уравнений на основе составления балансов массы и тепла в ходе процесса сушки. В этом

случае не рассматриваются поля влагосодер-жания и температуры внутри материала, а

ограничиваются их средними значениями.

dX ms ~T = - Qm dT               ,

dT ms ■ С— = QT — Qm dT где Х и Т – влагосодержание и температура; c -

удельная теплоемкость влажного материала;

Q m = A • J - конвективный поток влажности; m

d ( [ C s ⁺ Ci ' X ( T ) ]^ ^T ( T ) } =   ..    •[ T a — ^T ( T ) ] —

_ Am ' l ^ hm .  ।ФdB ' Pw" [ T (T )] | ms        [ Фа ' Pw" (Ta ) J

Второе уравнение содержит произведение дифференцируемых функций, которое преобразуем по формуле производной произведения функций:

dX (T) = — k . ln f ФdB ' Pw" [T (T)] । dT        ‘    [ Фа ' Pw" (Ta ) J                 (7)

_r        , .      -| dT ( t )          , , dX ( t )

I c • X ^{( T} ) + c s ^] . -T -+ _c , • T ^{( t} ) .       =

= k ₂ .Г t — t ( t ) ]— k • in | ^{Ф d B}'^Pw" ^{[ T (} T ^{) ]} I

^{2 [} a ^{v ]    3}          Ф • p (t)

I та Wwn У a / J где k = Am " hm ; k2 = AT " hT ; k3 = Am "l • hm .

ms         ms          ms

Подставляя значение производной влажности из первого уравнения во второе, получаем следующее выражение для температурной зависимости:

Q t = A • l • J_T - конвективный поток тепла; A и

m s – площадь поверхности и масса сухого материала; l – скрытая теплота испарения.

Удельные потоки массы и тепла на основе термодинамики необратимых процессов можно представить системой уравнений:

[ c , • X ( ^T ) ⁺ c s ]•

dT ( t ) d T

• T ( t ) • k • in

I ^Ф d B ' Pwn [ ^{T ( T} ) ] f [    ^ф а ' Pwn ( ^T a ) J

= k ₂-Г T — T ( t ) ] — k • in | ^{Ф d B} 'pw" ^{[ T (} T ^{) ] f 2 [ a        ;]    3}          Ф • p  (T)

I та ^p wn \ a ) J

= ^L11

(1      1

—

T T

V   »a

+ L 12

Г

S

I T

—

J m

= L 21

Рассматривая конвективную сушку с массопереносом между граничным слоем

влажного воздуха и сушильным агентом, пренебрегая эффектами Соре и Дюфора и соответственно L 12 = L 21 = 0, зависимости (2) и (3) принимают следующий вид:

J_T = h_T ( T . — T ) ,             (4)

V ^{T  T}a )        x 0         V a P wn T )

где h T = L 11 /T T a называют «коэффициентом конвективной теплопередачи»; h m = L 22 R называют «коэффициентом конвективной передачи пара»; R - газовая константа, x – мольное отношение концентрации пара в воздухе; Ф = (P w /P wh ) t относительная воздушная влажность и Р wn парциальное давление пара для влажного состояния.

которое нормализуем относительно производной от температурной зависимости:

c • T(t)• inIФdB pw" [ TT)]I dT (T) = k I 3 7    |  Фа ■ Pwn (Ta ) J             (9)

^{d T}      '           [ ^C I ' ^X ( ^T ) ⁺ c s ]

_ln | ^Ф d B ' P w" [ ^{T ( T} ) ] |

, .   [ T a — T ( T ) ]            |    ^ф а ■ Р ," ( ^T a )    J

² [ ^C I ' ^X ( ^T ) ⁺ c s ]     3      [ ^C I ' ^X ( ^T ) ⁺ c s ]

Таким образом, получена система нормальных уравнений следующего вида:

dX (T) = _k . ln f ФdB ' Pw" [T (T)] | dT        '    |   Фa ' Pwn (Ta ) J c, • T(t)• in|ФdB 'Pw" [T(T)]J dT (t )_                 I  Фa ' Pwn (Ta ) J dT      '          [C, ' X (T) + Cs ]         + h I ФdB ' Pw" [T (T)] I

₊ , ,   Г T a — T ( T ) ]  _        I   Ф a ■ P w" ( ^T a ) J

² [ ^C I • ^X ( ^T ) ^{+ C} s ]     ³      [ ^C I • ^X ( ^T ) ^{+ C} s ]

где относительная воздушная влажность на поверхности зерна определяется формулой:

^ ₅ b ={ 1 _— ( i _— ^ ) • ( X r — X ^)/( X r — X q ) ,    ⁽¹¹⁾

где верхнее значение для X > X_CT, а нижнее - для X cr > X > X eq , которое ограничивает пределы существования решения от влажности равной X cr до влажности равной X eq .

Необходимо также учесть сжатие материала в ходе сушки. Часто принимается линейная зависимость [6], которая после преоб- разования принимает вид:

AX ) = Г VX 1  =Г ( 1 - b ) X + b

A o L V J     L       X 0   .

2/3 n

0.0952 ■ Ln

Для идентификации параметров модели использовали экспериментальные данные по сушке семян риса в тонком слое, в которых изменялась температура сушки и скорость сушильного воздуха [7]. В качестве исходных данных использовались кинетические экспериментальные зависимости (Рисунок 1) , минимизируя сумму относительных отклонений экспериментальных данных (точки на Рисунок 1) от соответствующих расчетных кривых (линии на Ри сунок 1) для данных экспериментальных значений времени. Идентификация параметров производилась по методу Нелдера-Мида, также известного как метод деформируемого многогранника и симплекс-метод, метод безусловной оптимизации функции от нескольких переменных, не использующий производной (градиентов) функции, а поэтому он легко применим к негладким и/или зашумлённым функциям.

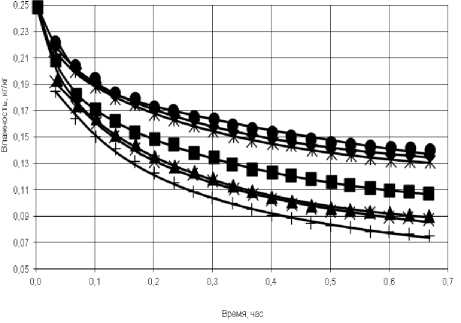
T50Xexp. кг/кг еТбОХехр, кг/хг жТ^ОХехр, кг/кг *V23Xexp. кг/кг xV28Xexp, кг/кг xW132Xexp, кг/кг +W)6Xexp. кг/кг

Рисунок 1. Кинетические кривые сушки риса

Изменение объема зерна определяется параметрами режима сушки. Изменение объема важно не само по себе, а в связи с трещин-новатостью [8], определяемой по регрессионной формуле (13):

X ( 0 ) - X ( т max )

max

X ( 0 ) - X ( т max )

г max

+ 0.4487

где X(0) – начальная влажность;  X(τmax) – конечная влажность; τmax - время сушки, час.

Используя полученную упрощенную модель термовлагомеханики сушки риса, провели моделирование процесса сушки в условиях минимальной трещинноватости в исследуемом диапазоне (температуры сушильного агента от 50 до 70 °C, скорости от 2.3 до 2.8 м/с). Для минимальной трещинноватость семян риса зависимости представлены на рисунке 2.

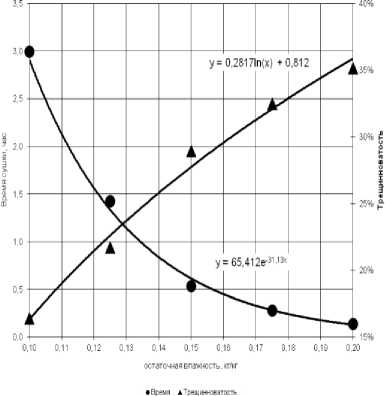
Рисунок 2. Аппроксимация объема и влажности от времени при режимах минимальной трещинноватости.

Трещинноватость логарифмически зависит от остаточной влажности и экспоненциально от времени сушки. Представленные зависимости позволяют прогнозировать качество семян риса в процессе сушки.