Моделирование рисков экономической безопасности регионов России в условиях санкционного давления

Начиная с 2014 года усиливается санкционное давление недружественных стран на российскую экономику, заключающееся в финансовых, торгово-экономических и иных ограничениях. Согласно Стратегии экономической безопасности РФ на период до 2030 года, использование таких дискриминационных мер относится к основным вызовам и угрозам, поэтому в условиях обострения геополитических противоречий со странами Запада особую актуальность приобретает выработка комплекса мер по нейтрализации возникающих рисков. По этой причине риски экономической безопасности нуждаются в исследовании, причем в региональном разрезе, учитывая значительную неоднородность субъектов РФ и особенности последствий санкционных ограничений для них.

Несмотря на достаточно длительный срок действия санкций, как справедливо отмечают Е.Т. Гурвич и И.В. Прилепский (Гурвич, При-лепский, 2016), нет единого мнения о масштабах последствий санкций для российской эко- номики не только на количественном уровне, но и на качественном. Более того, результаты опросов и различные расчеты эффектов демонстрируют широкий спектр оценок и зачастую являются противоречивыми. Так, например, в докладе Всемирного банка1, опубликованном в апреле 2023 года, снижение ВВП России по итогу года прогнозируется лишь на 0,2%, хотя еще в январе прогноз падения составлял 3,3%. Подобные изменения в оценке последствий санкционного давления вполне объяснимы бы-строменяющейся международной конъюнктурой, которая вносит свои коррективы. Очевидно, что в настоящее время исследование данной проблемы ограничено слишком большим количеством неизвестных «переменных», поэтому в рамках данной статьи поставлена цель провести моделирование рисков экономической безопасности регионов России в условиях санкционного давления.

Цель работы – описание модели многофакторного риска применительно к задачам мониторинга на примере оценки экономической безопасности регионов Уральского федерального округа (УрФО) в условиях санкционного давления.

Обзор литературы

Для рассмотрения рисков экономической безопасности территории в научной литературе используются как качественные, так и количественные методы оценки, имеющие свои преимущества и ограничения. С одной стороны, математические методы, применяющиеся для анализа неопределенностей, требуют значительного массива данных, которым не всегда располагают исследователи (Сошникова и др., 1999; Aven, 2019). С другой стороны, методы качественного анализа (метод экспертных оценок, SWOT-анализ, АВС-анализ и др.) для исследования социально-экономических систем допускают некий субъективизм (Васильев и др., 2015; Ильенкова, 2016; Каранина, Максимова, 2022; Benzaghta et al., 2021; Ginevicius et al., 2022). Также следует отметить экспертно-статистический байесовский подход, применяемый для сценарного прогнозирования развития территорий (Bryant, Zhang, 2016; Graziani, 2020).

В связи с этим, как справедливо отмечают ученые (Митяков, 2019; Лобкова, 2022), наиболее распространенным подходом к оценке рисков экономической безопасности является измерение отклонений отдельных показателей от установленных их пороговых значений. В зависимости от степени этого отклонения определяют различные уровни (зоны) риска. Так, например, В.К. Сенчагов и С.Н. Митяков (Сенчагов, Митяков, 2011) используют зонную теорию для ранжирования нормированных индикаторов по пяти зонам риска (катастрофический, критический, значительный, умеренный риск и стабильность). Для оценки рисков экономической безопасности в условиях цифровой трансформации региональной экономики Е.В. Лобкова (Лобкова, 2022) применила теорию нечетких множеств, согласно которой выбранные показатели должны быть рассмотрены как соответствующие или не соответ- ствующие определенному уровню экономической безопасности и риска с использованием количественных границ. В рамках такого подхода оценка рисков экономической безопасности сводится к количественному определению отдельных опасных исходов без учета вклада каждого фактора многомерной системы, то есть допускается, что они взаимно независимы, и пренебрегается вероятность их одновременного наступления. Методы адаптивной фильтрации и модели временных рядов обычно используются в задачах прогнозирования риска (Лукашин, 2003; Devianto, Fadhilla, 2015; Liu, Yu, 2022).

Также не учитывают взаимной зависимости факторов риска логико-вероятностные модели риска (Соложенцев, 2006; Cox, 2009). В последние годы стали успешно применяться копулы для моделирования зависимостей в управлении рисками предприятий, финансах, страховании (Cherubini et al., 2004; Joe, 2014). Однако поиск подходящей структуры копулы не является тривиальной задачей и требует больших выборок (Behrensdorf et al., 2019), что затруднительно реализовать в задачах анализа риска регионов из-за ограниченности данных.

Следует отметить, что факторы риска в общем случае выступают взаимно зависимыми и могут появляться одновременно, что приводит к росту последствий от их возникновения. Поэтому анализ экономической безопасности таких сложных многомерных стохастических систем, как экономическая безопасность регионов России, в условиях ограниченности данных и взаимосвязи факторов риска становится актуальной научной проблемой, а ее решение имеет теоретическую и практическую значимость.

Многофакторная модель анализа риска

Для анализа социально-экономической стабильности сложной многомерной системы воспользуемся моделью многомерного риска (Тыр-син, Сурина, 2017). Определим группу наиболее информативных факторов риска Х 1 ,Х 2 , .„,Х_т в достаточной мере описывающих возмущения системы, связанные с внешними и внутренними факторами. Таким образом, получим представление системы в виде случайного вектора X = (Х 1 , Х₂, ..., Х_т ) с некоторой плотностью вероятности p _x( x ), компоненты которого являются факторами риска.

На основе априорной информации выделим геометрические области неблагоприятных исходов, границы которых будут базироваться на пороговых значениях показателей, полученных путем экспертной оценки, и наилучших в смысле безопасности значениях 9 j , j = 1,2, .„, т . В случае отсутствия априорной информации о 9 , считаем их равными математическим ожиданиям Ц у = Мр^-] соответствующих показателей X j , то есть 9 у = Ц у , j = 1,2, .„, т . Тогда опасными ситуациями будем считать случаи больших и маловероятных отклонений выборочных значений Хц любой компоненты X j относительно 9 , и вероятность неблагоприятного исхода каждой из компонент X j будет определяться как

PQD) = P(Xy G Dy) = P(Xy е Dy), Dj = [x: d- < x < d+), где d-, d* — заданные на основе экспертных оценок левая и правая границы допустимых значений, ограничивающие область благоприятных исходов. При этом d- < d*.

Введем нижний Ь^- и верхний b + пороговые уровни допустимых отклонений относительно значений 9 , как b^- = 9 j - d^- и bj" = d j - 9 j , при этом соответствующие области благоприятных исходов D j для каждой компоненты X j будут описываться диапазоном (9 j - b^-< х < b + + 9 j ) .

Если задана только правая граница допустимых значений d + , считаем d j = -to и D_j = [х: х < dj') = (х: х < b j + 9_j } , иначе, при определении только левой границы d j , получим d j = +to и D j = [х: х >  dj } = (х: х > 9 j - b - } . Выражение d — = -го или d j = +to означает, что значения фактора риска X j менее или более 9 j являются такими же безопасными, как и X j (9 j ) .

Далее необходимо обобщить описанные выше определения для учета взаимного влияния компонент на появление неблагоприятных исходов путем их представления в виде многомерной области опасных ситуаций (зоны риска) D. D = Rm\D, где D — это область благоприятных исходов. Таким образом, оптимальным с геометрической точки зрения представлением области допустимых значений D будет m-осный эллипсоид следующего вида:

—

D =

{ т

X = (Х , , * 2..... Х т ): ^

/-1

-^ ^bi

I

с центром в точке 0 ' = (9 '1 , 9 ^ ,..., 9 ^ ) , причем Vj = 1,2, .„, т .

,; ■ 1«

((V

*■■=!

9 , ,	d-	■	—от V	d+ =
+ d^/2,	d -	>	—от Л	d+ <
+ 4^/2,	d "	>	—от Л	d+ <
b " ,			d + =	+от,
b + ,			d — =	— от.

+от,

+от,

+от,

Тогда для случайного вектора X вероятность неблагоприятного исхода будет равна

P(D) = P(XED),

( т

X = (% ! , %₂, .„, Х т ): ^

—

»Ь

¥

; ‘ ‘I

Следовательно, зона риска D будет представлять собой внешнюю область m -осного эллипсоида, полуоси по каждой из координат которого будут соответствовать одномерному случаю D j и равны b j соответственно. Очевидно, когда исход не лежит на одной из осей, то событие (X е D) может реализоваться и при отсутствии рисковых отклонений по всем компонентам (возможны ситуации X е D и V j X j ^ Dj) .

Для оценки единичного вклада показателя или группы показателей в вероятность P ( D )

введем

P(D^-) = P(D/D_k ), D^- = ^x^- = (X ! ,^, X k—i , X k+i ,^, x_m: Y^

( ^x j ^-e j)

^b J

£ *).

где D ^- — область неблагоприятных исходов после исключения одномерной области D_k , соответствующей фактору риска Х_к .

Тогда абсолютное и относительное изменение вероятности неблагоприятного исхода многомерной системы за счет добавления фактора Х_к равно

^P(D_k) = P(D) - P(D"), 5P(D_k ) = ^P(D_k)/P(D").

Оценка вероятности P(D) основана на использовании метода статистических испытаний Монте-Карло2. Суть этой процедуры состоит в следующем. Пусть имеем некоторую выборку данных в виде матрицы Xnхm, которую будем условно называть генеральной совокупностью. Обозначим ее плотность вероятности px(x). Мы должны многократно генерировать новые наблюдения z; = (zt1,..., zim) с законом распределения px(x). Тогда оценка вероятности P(D) будет равна частоте

М

P№ = IT где N – общее количество сгенерированных наблюдений zi (i = 1, ..., N), M — количество исходов, когда сгенерированное наблюдение Zk ED.

Для воспроизведения выборки X n _{х m} необходимо знать закон распределения многомерной генеральной совокупности. Будем считать его гауссовым. Во-первых, использование нормального закона распределения опирается на центральную предельную теорему ³ .

Во-вторых, такая идеализация не столь критична, и если есть какие-либо основания считать, что плотности вероятностей компонент случайного вектора X имеют более вытянутые хвосты, то это практически не скажется на числе исходов M (для нас важно лишь условие X е О ).

В-третьих, генеральная совокупность в данном случае будет относиться к малым выборкам, что делает невозможным даже приближенное оценивание закона распределения случайного вектора X .

Поэтому будем считать закон распределения p _x( x ) гауссовым. Тогда для нахождения его параметров оценим выборочную ковариационную матрицу 2_Х = (.^ач ) _{т х т} и вектор средних значений (Х_1Л..., Х_т) и будем считать их равными теоретической ковариационной матрице и вектору математических ожиданий соответственно. Генерацию случайного вектора Z = ( Z 1 , ..., Z m ) выполняем следующим образом:

z;k = У^акМ + Хк, к = 1,..., m, i = 1,..., N, где U 1, ... , Um — взаимно независимые, нормально распределенные случайные величины с нулевыми математическими ожиданиями и единичными дисперсиями. Приравняв cov(Zk, Zl) = cov(Xk, Xl) = okl и решив соответствующую систему из m нелинейных уравнений, получим формулы для расчета коэффициентов akj:

_ v¹ /-1 _ _

= ^«W, l < k, k . 1, _ , m akk =

j^-Z

k-1

j=1

^akj .

Очевидно, что распределения случайных векторов X и Z совпадают, т. е. p x ( x ) = p _z( x ). Поэтому имеем сходимость по вероятности выборочного распределения p_z (^х) сгенерированных модельных данных к распределению p _x( x ), и необходимый объем выборки для заданной надежности можно определить с помощью стандартных статистических критериев.

Использование ковариационной матрицы S _x для факторов риска позволяет учесть взаимосвязь между ними, что отличает данную математическую модель от известных моделей риск-анализа.

Учеными Института экономики УрО РАН (Куклин и др., 2018) был проведен анализ рисков для благосостояния в регионах Уральского федерального округа по ежегодным данным за 2001–2016 гг. Однако здесь был рассмотрен статический вариант риск-анализа. Представляет интерес перенести данный подход на динамический вариант, который позволит проводить текущий мониторинг риска по ежемесячным или ежеквартальным значениям социальноэкономических показателей, в оперативном режиме оценивать текущую ситуацию и своевременно формировать управленческие рекомендации при снижении экономической безопасности в регионах.

Данные оценки

Информационной базой исследования рисков экономической безопасности являются статистические данные Федеральной службы государственной статистики в разрезе субъектов РФ по месяцам с января 2016 года по март 2023 года. Выбор промежутка времени обусловлен наличием нескольких кризисных периодов и позволит увидеть емкую картину проявления нестабильности исследуемых систем. В таблице 1 представлен перечень

Таблица 1. Показатели экономической безопасности региона и их пороговые значения

Обозначение	Показатель, единица измерения	Пороговое значение
		«Мягкое»	«Жесткое»
X 1	Индекс промышленного производства, % к соответствующему месяцу предыдущего года	не менее 89	не менее 85
X 2	Объем работ, выполненных по виду деятельности «Строительство», % к соответствующему месяцу предыдущего года	не менее 86	не менее 80
X 3	Оборот розничной торговли, в сопоставимых ценах, % к соответствующему месяцу предыдущего года	не менее 90	не менее 85
X 4	Среднемесячная номинальная начисленная заработная плата работников организаций, % к соответствующему месяцу с учетом инфляции*	не менее 96	не менее 95
X 5	Уровень регистрируемой безработицы, процент	не более 4,6	не более 6,0
X 6	Индекс производства продукции сельского хозяйства, % к соответствующему периоду предыдущего года**	не менее 93	не менее 90
X 7	Объем инвестиций в основной капитал за счет всех источников финансирования, по полному кругу хозяйствующих субъектов, в сопоставимых ценах, % к соответствующему периоду предыдущего года**	не менее 86	не менее 85
X 8	Индекс производства по виду экономической деятельности «Добыча полезных ископаемых», % к соответствующему месяцу предыдущего года	не менее 85	не менее 80

* Пересчитан с учетом индекса потребительских цен.

** Интерполирован по квартальным данным.

Источник: составлено авторами.

показателей, используемых для моделирования рисков, составленный на основе показателей мониторинга и оценки экономической безопасности России, утвержденных Указом Президента РФ от 13 мая 2017 г. № 208. Для обеспечения устойчивости оценивания ковариационной матрицы число рассматриваемых факторов риска было ограничено восемью, влияние которых на экономическую безопасность оказалось наиболее существенным. Отметим, что в научной литературе (Серебренников и др., 2018; Павлов, 2019; Анисимов, 2022) состав утвержденных показателей подвергается критике, обосновываются предложения по его уточнению. Например, отдельные показатели в большей степени характеризуют благосостояние, поступательное развитие, а не риски. Тем не менее, для целей нашего исследования применение его сокращенного варианта (8 из 40 показателей) оправдано двумя причинами:

• •    наличие достаточно тесной корреляции между многими социально-экономическими индикаторами, поэтому риск-анализ по выделенной части показателей в целом позволяет адекватно оценить экономическую безопасность;

• •    на региональном уровне некоторые показатели из перечня недоступны, а часть публикуется не оперативно.

Хотя санкционное давление существенно отразилось на таких сферах, как строительство, инвестиции и добыча полезных ископаемых, при анализе рисков экономической безопасности в региональном разрезе показатели, характеризующие ситуацию в этих сферах (Х2, Х7 и Х8), не были рассмотрены, что связано с несколькими причинами. Во-первых, их помесячная динамика не является репрезентативной, более точную картину отражают годовые значения показателей, поскольку реализация различных проектов в российских регионах производится не на регулярной основе, а по мере востребования. В этом плане достаточно устойчивая картина наблюдается по среднероссийским значениям. Во-вторых, для отдельных регионов могут быть условно допустимы и приемлемы невысокие значения и динамика по показателям строительства, инвестиций и добычи полезных ископаемых. «Провалы» в этих сферах ниже порогового значения для региона не всегда могут означать наступление рисков, в то же время с позиции обеспечения экономической безопасности на уровне страны, вероятнее, выступают индикатором ухудшения состояния. В-третьих, регионы являются частью страны как системы, и с учетом разделения труда, разных климатических, географических, природных и иных условий для каждого региона часть показателей мониторинга экономической безопасности оказывается несущественной.

Предложенная модель многофакторного риска позволяет варьировать используемые факторы риска, поэтому в зависимости от задач исследования представленный в таблице 1 перечень показателей может быть изменен.

Отдельной методологической задачей исследования является определение пороговых значений показателей экономической безопасности. Для ее решения сложилось два подхода к содержанию категории «порог». Первый подход заключается в толковании порога как целевого приемлемого значения, примерами его использования являются Стратегия экономической безопасности РФ 1996 г.4 и Доктрина продовольственной безопасности РФ 2010 г.5; второй подход – как предельного значения показателя, широко используемого в теории экономической безопасности. Данное исследование построено на втором подходе, под пороговым значением понимается количественно определенное значение показателя, превышение которого сигнализирует о переходе экономической безопасности территории в качественно новое состояние.

Для установления порогового значения показателей экономической безопасности применяются различные методы: методы сравнительного анализа (сравнение с мировым или среднероссийским уровнем) и методы экспертных оценок (Лобкова, 2022). В научной литературе (Криворотов и др., 2019; Локосов, 2021) экспертные оценки выступают наиболее распространенным способом определения пороговых значений. Так, С.Ю. Глазьев и В.В. Локо-сов величину предельно критических значений устанавливают исходя из результатов специальных исследований, экспертных оценок и математического моделирования (Глазьев, Локосов, 2012). Также этот способ заложен в методоло- гию определения пороговых значений основных (приоритетных) факторов рисков и угроз экономической безопасности хозяйствующих субъектов, разработанную В.И. Авдийским и В.К. Сенчаговым (Авдийский, Сенчагов, 2014). С.Н. Митяков, Е.С. Митяков и Т.А. Федосеева (Митяков и др., 2020) использовали экспертные оценки и международные сопоставления при выборе пороговых значений. А.Б. Виссарионов и Р.Р. Гумеров (Виссарионов, Гумеров, 2017) недостатком метода экспертных оценок называют то, что каждый индикатор и его предельные значения рассматриваются изолированно от других индикаторов и без учета исторических аналогий. Поэтому в рамках нашего исследования пороговые значения были выбраны путем экспертной оценки, основанной на наиболее ярких кризисных явлениях в России в 1998 и 2009 гг. Кроме того, для более точной оценки рисков экономической безопасности рассмотрена методология, предложенная А.И. Татаркиным и А.А. Куклиным (Татаркин и др., 1997), позволяющая количественно оценить наличие, характер и уровень проявления риска и его динамику с помощью системы пороговых значений: от «мягких» – к более «жестким». Изначально выбранные «мягкие» пороговые значения, базирующиеся на кризисных значениях, в слабой степени отражают неблагоприятные ситуации регионов, поведение факторов рисков в которых более непредсказуемо и хаотично и аналогичный выход за пороговые значения для страны не будет однозначно определять кризисное явление для области. В связи с этим были ужесточены и определены «жесткие» пороговые значения, заданные в зависимости от степени колебания исследуемых факторов риска.

Оценка риска

Для исследования общих тенденций обеспечения экономической безопасности модель анализа рисков была апробирована на данных по России, а для выявления региональной специфики влияния санкционного давления – на данных по субъектам РФ. Модель реализована при помощи языка программирования C++ в среде Microsoft Visual Studio 2019. На рисунке 1 представлена оценка вероятности попадания показателей экономической безопасности России в зону риска.

Рис. 1. Оценка вероятности попадания показателей экономической безопасности России в зону риска

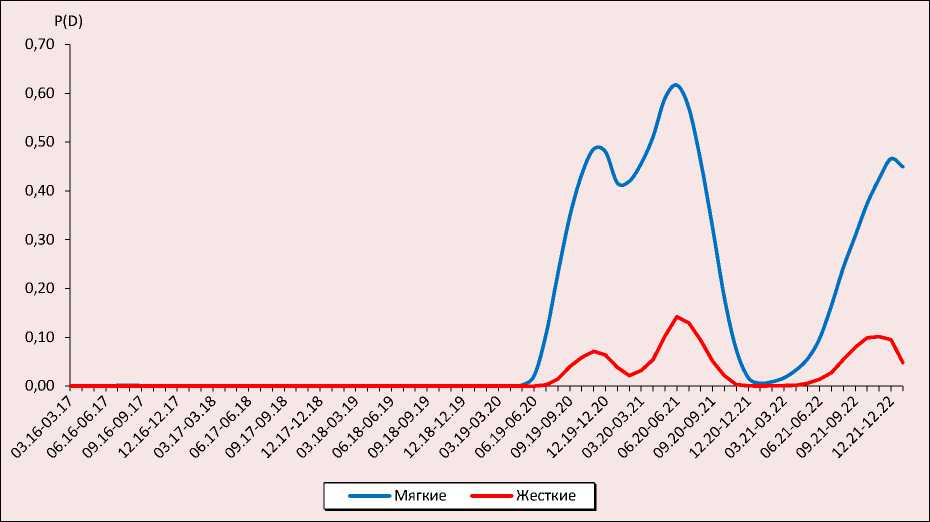
Источник: составлено авторами.

В связи с тем что исследование производится по ежемесячным данным, явно видны случайные отклонения и сезонные колебания, что может привести к смещению оценки риска. Для исключения влияния подобных выбросов с сохранением характера динамики показателей в анализе были использованы усредненные значения по шестимесячным периодам. Также, учитывая принцип генерации статистических испытаний метода Монте-Карло с применением ковариационной матрицы, в ходе исследования рассматривался период в 12 месяцев с шагом в 1 месяц, выбор которого обусловлен числом показателей в модели.

Таким образом, увеличение вероятности попадания в зону риска на рисунке 1 в точке 06.1906.20 (в период с июня 2019 г. по июнь 2020 г.) можно интерпретировать как включение в анализ кризисного месяца или первое проявление ухудшения состояния экономической безопасности в июне 2020 года.

Согласно динамике полученной оценки, четко выделяются два периода возрастания рисков экономической безопасности России. Первый период связан с двумя волнами панде- мии COVID-19 и введением ограничительных мер, второй – с усилением санкционного давления. В рамках анализируемого временного отрезка риски первого периода более значимы для обеспечения экономической безопасности страны. В связи с тем, что «мягкие» пороговые значения основываются на кризисных явлениях годовых показателей Российской Федерации, пики вероятности попадания в зону риска на рисунке 1 для них намного более ярко выражены, чем для «жестких».

Расчеты свидетельствуют, что основными факторами возрастания рисков экономической безопасности России в период пандемии стали спад розничной торговли ( X ₃), рост безработицы ( X ₅) и сокращение добычи полезных ископаемых ( X ₈). Пандемия коронавируса и меры, принятые для ограничения его распространения, привели к существенному сокращению розничного товарооборота в России. Так, по итогу 2020 года индекс физического объема оборота розничной торговли составил 96,8%, причем наиболее серьезный спад отмечен в апреле 2020 года (78,0% по сравнению с аналогичным периодом 2019 года). В «пандемийный»

период исследователи НИУ ВШЭ (Симачев и др., 2021) выделили несколько этапов кризиса розничной торговли, связанных с введением локдаунов, краткосрочным ажиотажным потребительским спросом, неготовностью к наращиванию онлайн-торговли, снижением платежеспособного спроса.

По итогу 2020 года уровень безработицы в России, рассчитанный по методологии МОТ, составил 5,8%, что является приемлемым значением и демонстрирует успешную нейтрализацию угроз пандемии в сфере занятости населения. В то же время отмечен беспрецедентный рост регистрируемой безработицы, вызванный расширением материальной поддержки безработных через службу занятости и упрощением процедур регистрации граждан в центрах занятости. Если до пандемии в службе занятости регистрировались не более четверти от общего числа безработных, то во втором квартале 2020 года поддержку государства получали уже почти две трети, а в третьем – почти три четверти безработных (Соболева, Соболев, 2021).

Введенные в России ограничительные меры привели к спаду спроса на энергоресурсы и, как следствие, к сокращению добычи углеводородного сырья. Например, в апреле 2020 года производство бензина сократилось на 20,1% по сравнению с апрелем 2019 года, а его продажи на АЗС – на 40–50%6. Кроме того, объем добычи полезных ископаемых резко снизился в мае 2020 года после заключения сделки в рамках ОПЕК+ о снижении нефтедобычи7.

Во втором «санкционном» периоде выявлены такие факторы возрастания вероятности ухудшения экономической безопасности, как сокращение розничного товарооборота (X3) и снижение уровня заработной платы (X4). Хотя для защиты внутреннего продовольственного рынка и стабилизации цен Правительство РФ ввело ограничения по вывозу ряда товаров из России, за 2022 год в результате проблем с логистикой, изменений потребительского поведения розничный товарооборот в среднем по России сократился на 6,5%. Кризисные явления заметно отразились на рынке труда, но если в период пандемии они сказались на росте безработицы, то в «санкционном» периоде – на падении оплаты труда, что более характерно для российского рынка труда. В.Е. Гимпельсон и Р.И. Капелюшников такой нестандартный режим адаптации рынка труда к шокам разной природы называют «российской моделью», когда ценовая адаптация доминирует над количественной (Гимпельсон, Капелюшников, 2015).

Очевидно, что в зависимости от специализации и социально-экономических особенностей в регионах России последствия санкционного давления для обеспечения экономической безопасности значительно варьируются. Согласно различным классификаторам регионов, в состав Уральского федерального округа входят субъекты РФ, которые относятся к различным типам. По мнению Ю.Г. Лавриковой, УрФО, во-первых, является срединным макрорегионом (занимает срединное положение в России), во-вторых, обладает уникальной территорией, в его структуре есть все типы регионов (Лав-рикова, 2017). Так, Курганская и Тюменская области8 представляют аграрно-индустриальный тип, Свердловская область – индустриально-торговый, Ханты-Мансийский и ЯмалоНенецкий автономные округа – энергосырьевой, Челябинская область – индустриальный.

На рисунках 2, 3 отражены расчеты оценки вероятности попадания показателей экономической безопасности субъектов УрФО в зону риска. Поскольку «мягкие» пороговые значения устанавливались исходя из годовых показателей страны, то расчеты, полученные на их основе, в меньшей степени отражают состояние экономической безопасности регионов и, соответственно, хуже описывают вероятность неблагоприятного исхода (см. рис. 2). Результаты оценки с использованием «жестких» пороговых значений (см. рис. 3) исключают отдельные всплески риска экономической безопасности, которые могут являться реакцией экономики региона на малозначимые возмущения. Поскольку в ходе исследования нами рассматриваются ежемесячные данные (а не ежегод- ные), подобные всплески оказывают достаточно сильное влияние на оценку рисков, то в этом случае целесообразно рассматривать в первую очередь оценку с «жесткими» пороговыми значениями.

Рис. 2. Оценка вероятности попадания показателей экономической безопасности субъектов УрФО в зону риска для «мягких» пороговых значений: 1 – Свердловская область, 2 – Челябинская область, 3 – Тюменская область, 4 – Курганская область, 5 – Ханты-Мансийский автономный округ, 6 – Ямало-Ненецкий автономный округ

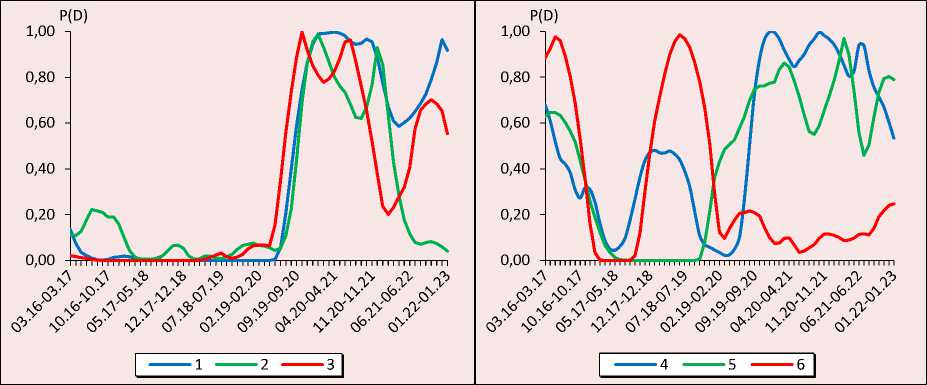
Источник: составлено авторами.

Рис. 3. Оценка вероятности попадания показателей экономической безопасности субъектов УрФО в зону риска для «жестких» пороговых значений: 1 – Свердловская область, 2 – Челябинская область, 3 – Тюменская область, 4 – Курганская область, 5 – Ханты-Мансийский автономный округ, 6 – Ямало-Ненецкий автономный округ

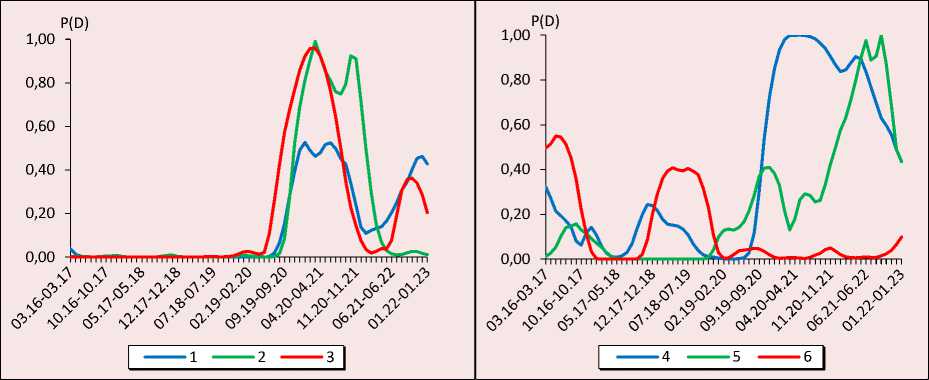
Источник: составлено авторами.

В результате проведенного анализа видно, что в целом динамика показателей экономической безопасности и факторы повышения рисков по отдельным субъектам округа совпадают. В таблицах 2 , 3 приведены сгруппированные факторы, внесшие наибольший вклад в увеличение риска экономической безопасности субъектов округа.

Согласно полученным расчетам на основе «жестких» пороговых значений выделены два явных пика повышенных рисков экономической безопасности в Свердловской и Тюменской областях, связанные с влиянием последствий пандемии и ужесточения санкционного давления. В оба эти периода значимым фактором стало сокращение объемов производства сельского хозяйства (X6), а в Свердловской области также отмечается спад розничного товарооборота (X3). Кроме того, в период пандемии наибольший вклад в ухудшение состояния экономической безопасности Свердловской и Тюменской областей внес рост регистрируемой безработицы (X5). Если ухудшение динамики показателей розничного товарооборота и безработицы характерно для кризисных периодов в целом российской экономики, то сокращение объемов сельскохозяйственного производства вызвано региональными особенностями. В Свердловской области с III квартала 2020 года по II квартал 2022 года снижались объемы производства сельскохозяйственной продукции. Сначала сократилось производство продукции растениеводства в результате природно-климатических условий, которые привели к уменьшению урожайности зерна, картофеля и овощей (табл. 4), а затем вследствие карантинных и санкционных ограничений произошел спад объемов продукции животноводства (табл. 5), зависящей от импорта оборудования, племенного скота, семенного материала (Кабанова, 2023). Во второй половине 2022 года сельское хозяйство Свердловской области адаптировалось, по итогам года отмечался рост производства продукции сельского хозяйства на 8,9%

Таблица 2. Факторы, внесшие наибольший вклад в повышение риска экономической безопасности Свердловской, Челябинской и Тюменской областей

Субъект УрФО	Кризисный период
	2020–2021	2022
Свердловская область	(0.23) (0.26) (0.14)	(0.38) (0.19)
Челябинская область	(0.12) (0.1) (0.84)	–
Тюменская область	(0.42) (0.2)	(0.19)
Примечание (здесь и в табл. 3): в скобках указан абсолютный единичный (обособленный, частный) вклад, рассчитанный по формуле (1). Источник: составлено авторами.

Таблица 3. Факторы, внесшие наибольший вклад в повышение риска экономической безопасности Курганской области, Ханты-Мансийского и Ямало-Ненецкого автономных округов

Субъект УрФО	Кризисный период
	2016–2018	2018–2020	2020–2023
Курганская область	(0.1)	(0.1) (0.23) (0.28)	(0.12) (0.65)
Ханты-Мансийский автономный округ	(0.15) (0.16)	(0.3) (0.27)	(0.97)
Ямало-Ненецкий автономный округ		(0.37)	–
Источник: составлено авторами.

Таблица 4. Урожайность зерновых и зернобобовых культур, ц с 1 га убранной площади

Территория	2016	2017	2018	2019	2020	2021	2022
Российская Федерация	26,2	29,2	25,4	26,7	28,6	26,7	33,6
Уральский федеральный округ	16,2	19,2	16,1	16,9	13,8	12,1	21,4
Курганская область	16,3	18,6	16,2	16,9	13,5	11,1	21,9
Свердловская область	17,7	22,5	19,4	22,3	20,9	16,7	27,5
Тюменская область	18,8	23,3	20	22,4	19,9	16,3	26,7
Челябинская область	14,5	16,8	13,4	13	8,6	9,2	16,5
Источник: данные Росстата.

Таблица 5. Индекс производства продукции животноводства, %

Территория	2016	2017	2018	2019	2020	2021	2022
Российская Федерация	101,6	102,6	101,1	101,9	101,9	100,0	102,4
Уральский федеральный округ	101,3	101,1	101,7	100,5	97,5	97,0	99,2
Курганская область	98,3	97,4	99,5	98,5	100,7	90,1	92,4
Свердловская область	99,9	104,0	100,7	102,5	102,1	96,6	101,7
Ханты-Мансийский автономный округ	101,3	101,7	96,1	98,8	96,7	91,8	86,9
Ямало-Ненецкий автономный округ	99,3	105,5	96,2	99,0	105,5	120,3	109,1
Тюменская область	98,7	102,4	104,2	104,0	99,6	101,9	99,8
Челябинская область	104,1	99,4	102,0	98,1	92,5	95,3	98,6
Источник: данные Росстата.

(растениеводства – на 20,6%, животноводства – на 1,7%) в результате реализации «защитных» правительственных мер, рекордного урожая зерновых культур, а также из-за «низкой» базы сравнения. В других субъектах округа в сельском хозяйстве за анализируемый период наблюдалась аналогичная ситуация.

Согласно полученным оценкам, в Челябинской области четко прослеживается рост рисков экономической безопасности только в период пандемии, причем с выделением двух волн. Факторами, оказывавшими влияние на такой рост, стали снижение заработной платы, скорректированной на инфляцию ( X ₄), объемов сельскохозяйственной производства ( X ₆) и увеличение регистрации граждан в центрах занятости ( X ₅). Рынок труда адаптировался к социально-экономической нестабильности как за счет уво льнений работников, так и в результате применения неполного рабочего дня, сокращенной рабочей недели. В период усиления ан-тироссийских санкций вероятность ухудшения состояния экономической безопасности области не выявлена.

Результаты оценки вероятности достижения показателями Курганской области «жестких»

пороговых значений свидетельствуют, что с точки зрения обеспечения экономической безопасности среди субъектов УрФО регион в значительной степени подвержен различным рискам. Выявлено три пика повышенных рисков экономической безопасности. Первый пик в Курганской области наблюдался в 2016 году, когда внешний шок в 2014–2016 гг. вызвал в России рецессию (Голяшев и др., 2017). В 2016 году наиболее значимым фактором был продолжающийся спад уровня оплаты труда ( X ₄). В 2018 году в период стагнации российской экономики (Цухло, 2019) фиксируется второй пик, связанный с ростом регистрируемой безработицы ( X ₅), сокращением объемов в промышленном производстве ( X ₁), а именно в производстве пищевых продуктов и готовых металлических изделий, а также в сельском хозяйстве ( X ₆). В период пандемии (третий пик) основными факторами роста рисков экономической безопасности являлись спад промышленного ( X ₁) и сельскохозяйственного ( X ₆) производства. В пределах анализируемого временного отрезка негативного влияния ужесточения санкций недружественных стран на обеспечение экономической безопасности в Курганской области не установлено.

В Ханты-Мансийском автономном округе выявлено несколько периодов увеличения рисков экономической безопасности. Пик первого периода фиксируется в 2016 году, когда девальвация рубля 2014–2015 гг. и введение продовольственного эмбарго привели к экономическому спаду, росту потребительских цен и, соответственно, к снижению доходов населения и потребительского спроса, что выразилось в сокращении оборота розничной торговли ( X ₃) и уровня заработной платы ( X ₄) в автономном округе. Второй период начался в 2019 году, негативно отразившись на динамике объемов промышленного ( X ₁) и сельскохозяйственного ( X ₆) производства, и усилился в 2021 году (практически единоличный вклад X ₆). Поскольку основную долю в обрабатывающем производстве Югры занимает производство по переработке нефти, газа и газового конденсата, то снижение экономической активности в периоды нестабильности отражается в сокращении его объемов. В схожем по специализации ЯмалоНенецком автономном округе такого сокращения не отмечается, поскольку за рассматриваемый период произошло увеличение добычи в результате освоения новых нефтегазоконденсатных месторождений – Новопортовского и Восточно-Мессояхского и выхода на плановую мощность крупнейшего нефтегазового завода «Ямал СПГ» (Колпаков, Сафина, 2020). В целом самые высокие показатели вероятности риска Ямало-Ненецкого автономного округа выявлены в 2016 году с наибольшим влиянием сокращения оборота розничной торговли ( X ₃) и в 2018 году в результате снижения объемов производства животноводства ( X ₆). Значимого ухудшения экономической безопасности автономных округов Тюменской области в период усиления антироссийских санкций не выявлено.

Заключение

На экономическую безопасность регионов влияет множество разнообразных факторов риска, которые часто оказываются взаимосвязанными. С целью их оценки и анализа в рамках данного исследования предложена многофакторная модель. Моделирование рисков экономической безопасности регионов России проведено на примере субъектов Уральского федерального округа. Полученные результаты свидетельствуют о возможности использовать рассмотренную модель многофакторного риска для изучения динамики экономической безопасности регионов России.

Установлено, что если для страны в целом наблюдается достаточно устойчивая картина, выражающаяся в стремлении показателей экономической безопасности находиться в рамках своих пороговых значений, то на региональном уровне ситуация варьируется. Среди субъектов УрФО наиболее подвержены влиянию рисков Курганская область, характеризующаяся низким социально-экономическим потенциалом, и автономные округа Тюменской области, экономика которых существенно зависит от внешнеэкономической конъюнктуры.

Ужесточение санкций недружественных стран оказало негативное влияние на обеспечение экономической безопасности как России в целом, так и отдельных субъектов УрФО. Однако в рамках анализируемого периода создаваемые риски существенно ниже в сравнении с последствиями пандемии COVID-19 и имеют тенденцию к сокращению. Согласно результатам регионального анализа, наиболее значимым фактором выступает состояние сельского хозяйства. В 2022 году именно этот фактор в субъектах округа (за исключением Челябинской области и Ямало-Ненецкого автономного округа, где ухудшение ситуации не выявлено) внес наибольший вклад в повышение риска. Но его влияние спало к концу года благодаря существенным антисанкционным мерам, направленным на поддержку бизнеса и граждан, а также в связи с рекордной урожайностью.

Важно отметить, что полученные результаты моделирования рисков экономической безопасности регионов России могут являться кратковременным следствием проведения анти-санкционной политики и не позволяют сделать однозначные выводы о достижении пиковых значений и стремлении системы к стабилизации. Очевидно, что влияние санкционного давления на обеспечение экономической безопасности регионов имеет долгосрочный характер и потребует проведения дальнейших исследований.