Моделирование стохастических систем дифференциальных уравнений с переменными запаздываниями
Автор: Печнова Софья Сергеевна, Полосков Игорь Егорович
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 3 (11), 2012 года.
Бесплатный доступ
Рассматриваются вопросы использования метода статистического моделирования (Монте-Карло) для численного исследования нелинейных систем стохастических дифференциальных уравнений с переменными запаздываниями. Приведены примеры анализа систем различного порядка. Произведено сравнение результатов расчетов для линейных систем с кусочно-постоянными запаздываниями, полученных рассматриваемым методом и на основе схемы расширения фазового пространства. Расчетные алгоритмы реализованы на входном языке пакета компьютерной алгебры Mathematica.
Моделирование, линейная система, стохастическое дифференциальное уравнение, запаздывание, нелинейная система, случайное возмещение, винеровский процесс, метод статистического моделирования, метод расширения фазового пространства
Короткий адрес: https://sciup.org/14729802
IDR: 14729802 | УДК: 519.6
Текст научной статьи Моделирование стохастических систем дифференциальных уравнений с переменными запаздываниями
Важным классом моделей, описывающих явления окружающего нас мира, являются дифференциальные уравнения (ДУ) с отклоняющимися аргументами. Среди этих уравнений присутствуют уравнения с запаздыванием, нейтрального типа и с опережением [1]. Запаздывания в этих уравнениях, позволяющие учесть подчиненность будущего не только настоящему, но и прошлому, могут быть и постоянными, и изменяющимися - функциями как независимой переменной, так и самой неизвестной функции и ее производных.
Работа выполнена при частичной финансовой поддержке РФФИ, проект № 11-0196024.
-
(с) Печёнова С. С., Полосков И. Е., 2012
Исследования качественных и количественных свойств детерминированных уравнений с запаздыванием развиваются в различных направлениях. Полученные при этом результаты находят широкое применение в задачах моделирования процессов автоматического управления; биологии и экологии, радиолокации и радионавигации; динамики экономических и социальных систем; горения в жидкостно-реактивных двигателях; влияния излучений [1-4] и т.д. Как правило, точные аналитические решения ДУ с запаздыванием могут быть найдены очень редко, причем известный метод шагов [1] пригоден только для постоянного лага. Численное же интегрирование таких уравнений требует разработки специальных вариантов методов Рунге-Кутта для обычных и жестких систем уравнений, часто весьма изощренных [5,6].
Благодаря развитию методов анализа детерминированных систем, ставших уже классическими, относительно недавно возник интерес к стохастическим ДУ (СДУ) с различными формами запаздывания [710]. Но исследование таких систем вызывает значительные трудности. Единственно более или менее широким классом стохастических систем с отклоняющимися аргументами, для которого процедура решения не очень сложна, является множество линейных систем с аддитивными шумами и одним постоянным запаздыванием. Так, уравнения для первых моментов фазовых координат были построены и решались в работе [11] с помощью аналога классического метода шагов.
Универсальной приближенной схемой, позволяющей исследовать СДУ с запаздываниями всех классов, является метод Монте-Карло (статистического моделирования) [12-15]. Но различные алгоритмы, предназначенные для численного интегрирования даже простейших стохастических дифференциально-разностных уравнений, как правило, весьма сложны [16, 17] и предназначены только для решения достаточно узких классов задач.
В настоящей работе рассматривается прямой алгоритм метода статистического моделирования для стохастических систем с переменными запаздываниями. Данный алгоритм базируется на стохастическом обобщении метода Хойна (Heun) [18]. Полученные в результате статистической обработки первые моменты векторов состояния линейных систем с кусочно-постоянными запаздываниями сравнивались с полученными с помощью комбинации метода шагов и расширения фазового пространства (МШРФП) [19]. Расчетные алгоритмы были реализованы на входном языке пакета компьютерной алгебры Mathematica [20].
1. Постановка задачи
Рассмотрим систему, описываемую системой СДУ (в смысле Стратоновича [21]) с переменными запаздываниями Tk ( t ) С 0 ( k = 1, 2, ..., d ) следующего вида:
d X ( t ) = f ( X ( t ) , X T 1 ( t ) ,..., X Td ( t ) ,t ) dt +
+G (X (t), X t i( t),..., X Td (t) ,t) о dW (t), t > tо, X(tо) = X0;
d X ( t ) = f о ( X ( t ) ,t ) dt +
+ G о( X ( t ) ,t ) о d W ( t ) , (2)
t
*
Здесь t - врсмя. X ( t ) E Rn - векторный слу чайный процесс, характеризующий поведение исследуемой системы,
X тк ( t )= X ( t - Tk ) , 1 С k С d,
t * = min [ t - Tk ( t )] , t > t о ,k
X 0 и X * - векторные случайные величины с известными распределениями, W ( t ) E R m - стандартный векторный нормальный винеровский случайный процесс [21]: E[ W ( t )] = 0. E[ W ( t ) W T ( t ' )] = t• 6 ( t-1 ' ) • I. f ( , , ..., , ■ ). f o ( •, ■) 11 G ( •, •,..., •, ■). G o ( •, ■) - неслучайные векторные и матричные функции соответственно, E - символ математического ожидания, I - единичная матрица соответствующего порядка, T - символ транспонирования матриц.
Заметим, что в стандартных постановках задач вместо уравнения (2), определяющего поведение вектора X ( t ) на на чальном множестве E. обычно использу ются соотношения X ( t ) = h ( t ), г де h ( t ) - неслучайная вектор-функция. Несложно увидеть, что рассматриваемый случай содержит стандартные постановки.
Задача состоит в построении реализаций случайного вектора X ( t ), статистической обработке результатов моделирования и демонстрации переходных режимов в компактной форме.
2. Схема Хойна для СДУ с переменным запаздыванием
Для численного интегрирования системы СДУ с переменным запаздыванием (получения реализации векторного случайного процесса, описывающего состояние системы) воспользуемся стохастическим аналогом метода Хойна. Представим его расчетные формулы для системы ДУ без запаздывания dY(0) = f *(Y(0),0) d0+
+ G * ( Y ( 0 ) ,0 ) о d W * ( 0 ) , 0>0 о , (3)
Y (0 о) = Yо в следующем виде [18]:
у ( 6 ) = у ( 0 ) + f * ( у ( 0 ) ,0 )А 0 +
+G* (у (0) ,0) и (0), у (0 + А 0) = у (0)+
+2 [f *(у(0), 0) + f *(у(0), 0 + А0] А0+ +|[G*(у(0),0) + G*(у(0),0 + А0)] х х и* (0), 0 > 0о,
У (0 о) = у 0, где А0 - шаг диыфстизаппи. у0. у(0) и и* (0) = Аw* (0) - результаты моделеро-вания векторных случайных величин Y и процессов Y(0), АW* (0) соответственно. Приближенное решение системы С ДУ (3), вычисленное с помощью последних соотношений, сходится к точному в среднем квадратическом с первым порядком по А0.
Простейшая схема интегрирования системы уравнений (1), (2) с помощью выбранного интегратора будет состоять в замене заданных переменных запаздываний кусочнопостоянными функциями со "ступеньками" ширины т = const > Си синхронизации шага интегратора А t с т: для этой синхронизации обе эти величины выбираются одинаковыми, но так, чтобы они были достаточно малы. Это требуется для получения необходимой точности представления т^ ( t ) и вычислений по формулам интегратора.
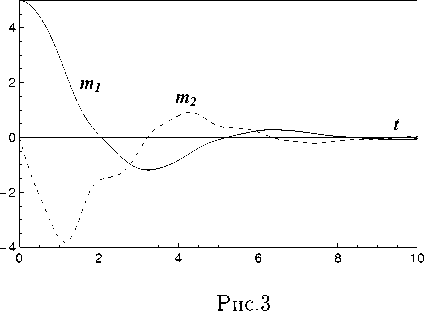
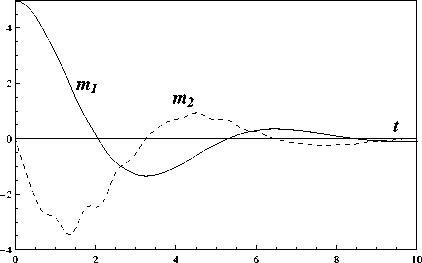
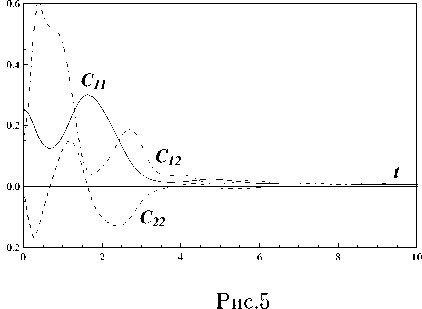
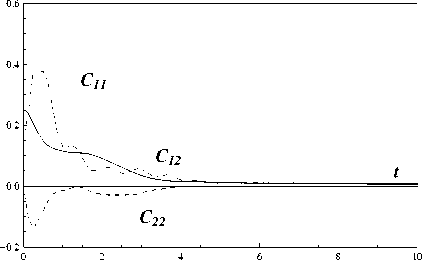
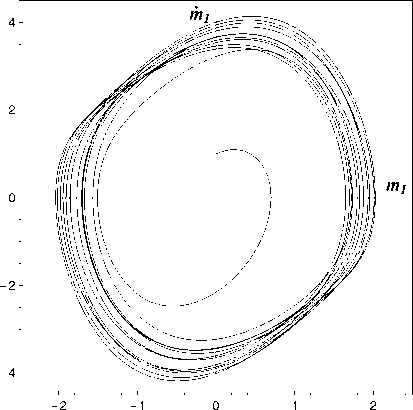
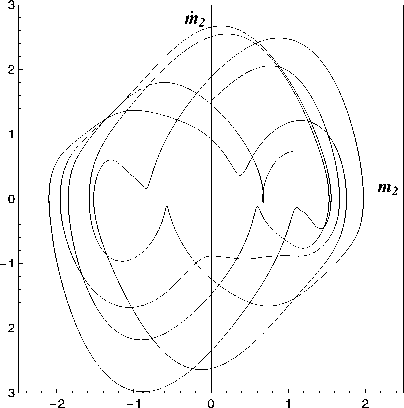
При таких условиях запаздывания т^(t) можно представить в виде тк (t)= Nkq т, tq-1 Nkq G{ С, 1, 2,...}, tq = 10 + q • т, т = t0 - t* , N0 = max Nkq., ( ) N 0 k,q q = 1, 2,... Тогда замкнутые расчетные формулы для [ e ] получения реализации {xq } на равномерной временной сетке tq = t0 + q • т. q = 0. 1. 2 N0. N0 + 1 N £ = 1. 2 L. будут выглядеть следующим образом: 1°. Для q = 0. 1. .... N0 - 1 [ e] [ e ] x q+1 xq+ + 2 [f 0(X[q],tq) + f 0(X[q],tq +1)] т + + 2 [G0(x[я],tq) + G0(xq],tq+1)] uq, [ e ] * X 0 = X . 2°. Для q = N0. 1..... N - 1. ... X qe ] = X qe ] + f q 1 т + Gq 1 Uq, Xq+ = Xqe] + 2 (f q 1 + f q2) т + + 2 (Gq 1 +Gq2) uq, X N1 = X 0, f q 1 = f ( X [q ], XЩ,..., X [d,tq ) , f q 2 = f ( X [q ], X qi], ..., X qd ,tq +1) , Gq 1 = G ( X qe], X qy..., X [d,tq ) , Gq 2=g ( x qe], xqy..., x qej,tq+1), x[e] = ж[ e Xqk Xq-Nk,q-N0 , k 1, 2,...,d, где uqi ~ N(С,т). i = 1, 2,...,n. - нормально распределенные случайные величины с нулевыми математическими ожиданиями и дисперсиями, равными т. После получения реализаций {х[q]} на основании соотношений описательной статистики на той же равномерной временной сетке можно вычислить несмещенные оценки компонент вектора математических ожиданий (i. j = 1. 2.....n) 1 L 1 [ e ] miq = Ll^xiq e=1 и ковариационной матрицы 1L Cijq = L-1 ^( x iq1 - miq )(x jq1 - m™) ■ e =1 Рассмотрим систему линейных СДУ с кусочно-постоянными запаздываниями тк(t) следующего вида: d XX(t) = P(t) X(t) + £ Qk(t) XTk(t)+ k=1 +c (t) + H( t) W( t), t>t 0, X (10) = X 0, где вид запаздываний Tk определен в предыдущей секции. Будем считать, что на интервале (t*,t0) вектор состояпия X(t) удовлетворяет системе СДУ без запаздывания: X(t) = P0(t) X(t) + c0(t) + +Ho(t) W(t), X(t*) = X*, причем в уравнениях (5) и (6) P(t), Qr(t), H(t). Po(t). Ho(t) 11 c(t). co(t) - известные непрерывные матричные и векторные функции. Кроме того, предположим, что известны все необходимые числовые характеристики случайных векторов X0 и X*. В частности, пусть в начальный момент времени t* для вектора X заданы вектор математических ожиданий m* = E[X*] и ковариационная матрица C* = E[(X* — m*)(X* — m*)T]. а остальные обозначения совпадают с введенными в первой секции. Методика состоит в построении систем обыкновенных дифференциальных уравнений (ОДУ) без запаздывания для компонентов вектора средних m(t) = E[X(t)] и ковариационной матрицы C(t) = E [{X(t) — m(t)}{X(t) — m(t)}T] фазовом) вектора X при любом t ^ t*. Для того чтобы получить СДУ без запаздывания, применим сочетание метода расширения фазового пространства и метода шагов. Рассмотрим равномерную временную сетку tq = t* + q • t. q = 0. 1. 2..... N. ... ii введем новую временную переменную s, изменяющуюся на промежутке [0,т], а также следующие обозначения: sq — s + tq—1,Aq — (tq—1, tq], Xq ( s )— X ( Sq ) , Wq ( S )— W ( Sq ) , Xq (0) — Xq—1(T) , Wq (0) — Wq—1(T) , col(XI,..., XN—I, XN) — — {X 11,X 12, .. X1 n, .. XN -1,1 ,XN-1,2, ..., XN -1,n, XN1 ,XN2, ...,XNn}T. Обратимся к последовательности полуинтервалов (сегментов) Aq. 1°. На сегменте A1 систему СДУ решением которой является случайная векторная функция Z 1(s) — X 1(s), можно записать в следующем виде (здесь и далее точкой обозначена производная по переменной s): Z 1(s)— [р1(s) + Q 1(s)] Z 1(s) + + f 1( s) + H 1( s) V 1( s), Z 1( s) — X 1( s), V 1( s) — W 1( s), P1( s) — P11 (s) — P0( s 1), Q1( s)— 0, f 1(s ) — f 1(s ) — c 0(s 1), H 1( s) — H11( s) — H0( s 1). 2°. На проможамках A1 11 A2 система’ еду X 1(s) — P0(s 1) X 1(s) + c0(s 1) + H0 (s 1) W 1(s), X2(s) — P0(s2) X2(s) + c0(s2) + H0(s2) W2(s) можно представить так: Z2(s) — [P2(s) + Q2(s)] Z2(s) + +f2(s) + H2(s) V2(s), Z 2(s) — X1(s X2(s ) ) , V2 (s) — 1- • , . -1 W 1( s) [ W2(s) J, — P2( s ) — P11(s) 0 P 0 22(s) ,P22( s ) — P0( s 2), — Q 2 (s) — [ 0 0 1 00, — f 2(s) — f 1( s) f2(s) . , f 2(s ) —c0(s2), — H2(s) — H11(s) 0 0 H22( s ) , H22 (s) — H0( s 2) (N0)0. Ha полуинтервалах A1, A2, ..., An0систему СДУ X 1(s) — P0(s 1) X 1(s)+c0(s 1) + H0 (s 1) W 1(s), X2(s) — P0(s2) X2(s)+c0(s2) + H0(s2) W2(s), X N0 (s ) — P0(sn0 ) X N0 (s) + c0(sn0 ) + + H0(sn0 ) WN0 (s) можно записать так: ZN0 (s) — [PN0 (s) + QN0 (s)] ZN0 (s) + + f N0 ( s ) + H N0 ( s ) V N0 ( s ), Z N0 ( s ) = ' X 1( s) X 2( S ) , X N0 (S ) V N0 ( s ) = ■ W 1( s) W 2( S ) , L VW N0 ( S ) J PN0 ( s ) = PN0-1(S) 0 0 PN0 N0 ( s ) , QN0 ( s ) = [ QN0-1(S) 0 01, f N0 ( s ) = P 1( s) f 2(s ) , f N0 ( s ) = = C o ( SN0 ), 1 f N0 (S) HN0 ( s ) = HN0-1(s) 0 0 HN0 N0 ( s ) , PN0N0 (S) = Po(SN0 ), HN0N0 (S) Ho (SN0 ) (Nо+1)°- На псшуотрезках А^ А2. An0. А nо+1система С ДУ XX 1(s ) = Po(s 1) X 1(s )+ cо (s 1) +Ho(s 1) VW 1(s), XX2(s) = P0(s2) X2(s) +c0(s2) +H0(s2) VW2(s), XN0(s) = Po(SN0) XN0(s) + co(SNо) + + Ho(SN0 ) WN0 (S), XN0+1(s) = P(SN0+1) XN0+1(s) + d +У? Qk(sN0+1) XN0+1 -Nk 1 (s) + k =1 + C(SN0+1) + H(SN0+1) WN0+1(S) принимает вид Q N0+1 (s )= QN0 (S О 0 QN0 +1 (S) QN0+1,N0+1(S) QN0+1(s) = [QN0+1,1(s) QN0+1,2(s) .. ...QN0+1 ,N0(s)], d QN0+1 ,r(s) = ^Qk(SN0+1) Sr,N0+1 -Nki, k=1 r = 1, 2 ,...,No + 1, fN0 ( S )4 / N0 ( S)+ 1, fN0 + 1( S ) = C ( SN0 + 1), f N0+1(s) [ H n0 ( s ) 0 1 HN0+1( s) = , 0 HN0+1 ,N0+1( s) HN0+1 ,N0+1(s ) = H(SN0+1). №. На (•(тмситах A1. A2.....AN0. AN0+1. An система СДУ X 1(s) = Po(s 1) X 1(s)+co(s 1) + Ho(s 1) VW 1(s), X2(S) = Po(s2) X2(S)+ Co(S2) + Ho(s2) W2(S), XN0 (S) = Po(SN0 ) XN0 (S) + Co(SN0 ) + + Ho(SN0 ) WN0 (S), XN0+1(s) = P(SN0+1) XN0+1 (S) + d +У?Qk(SN0+1) XN0+1 -Nk 1 (s) + k=1 + C(SN0+1) + H(SN0+1) WN0+1(S), XXN(S) = P(SN) XN(s) + d +У2 Qk(SN) XN-Nk 1 (s) + k=1 + C(SN) + H(SN) VWN(S) ZN0+1(s) = [PN0+1(s) +QN0+1(s )] ZN0+1(s)+ +f N0+1( s) + HN0+1(s ) V N0+1( s), Z N0+1( s )= [ x N0 (s Д 1, X n0+1(s) V N0+1( s )= [ V N0 (s) 1, W N0+1(S) записывается так: ZN(S) = [PN (S) + QN(S)] ZN(s) + + P N ( S ) + H N ( S ) V N ( S ), Z N ( S ) ZN-1(S) X N ( s ) PN0+1(s ) = PN0 (s) 0 PN0+1 ,N0+1( s) PN0+1 ,N0+1(s ) = P(sN0+1), V N ( S ) PN( s ) = [ V N -1( S ) VW N ( S ) PN-1(S) PNN ( S ) , PNN ( S ) = P( SN ), Q N ( S ) = ^ Q N-1(S) Q N ( s ) QN (s) = [QN 1( s) 0, QNN ( S ) , QN 2(S ) ... ...QN,N-1(S)] , числовые характеристики вектора Z + удовлетворяют следующим системам ОДУ: d QNr(S) = ^ Qk(SN) $r,N-NktN-n0 , k=1 r = 1, 2 ,...,N, fN(S ’ = [ T'-S S ) 1 f N( S ) , f N (S ) = C(SN ), -—_ — H N ( S ) = r- ---- . . H N ( S ) HNN (S ) _ , m + (S) = (р+ + Q+) • m +(S) + f +, C1+(S) = (р+ + Q+) •K +(S) + + [(P + + Q+ ) •C +(S)] T + H + H+T m+(0) = [ m∗ m∗ , C +(0) _ [C * C *] = C*C* , где P'=[ 00 0 р1 ]’ Q+ = [ 0 0 0 Q1 ] ’ f+ = 0 — [ f1 J , H + = ■ 0 0 ■ 0 H1 . . HNN ( S ) = H( SN ). Итак, получена цепочка систем линейных СДУ для расширенных векторов состояния Z1. Z2..... Zn- ■■■ увеличиватошейся размерности и одинаковой структуры без запаздывания. Теперь построенную последовательность систем линейных СДУ без запаздывания можно использовать для получения новой цепочки уравнений - ОДУ для первых моментов векторов Z r 11 Z + = col (X0, Z r^. r = 1, 2, ... , причем Подобные уравнения для вектора Z + выглядят так: m+(S) = (р+ + Q+) •m + (S) + f+, C+( S ) = (р+ + Q+) •C2+( S ) + _i_ 17 + +) r+ ]T + + t + P2 + Q2 1 • C2 (S) +H2 •H2 , m +(0) = m∗ m∗ mx 1 (т) C 2+(0) = C∗ C∗ Cx1x0 (т) C * Cx 0 X1 (т) C * Cx 0 x 1 (т) CX 1 x 0 ( т ) Cx 1 x 1 ( т ) mr(s) = E [Zr] = col(mx 1, mx2,..., mXr), m+(s) = E[Z + ] = col(m*, mr (s)), Cr ( s ) = E[( Z r — mr)(Z r — mr) T ] = где P + - P2 = —— [ 0 —P2 ]’ Q+ = 0 Q—2 , ≡ CX1X1 CX2X1 ... CXrX1 CX1 X2 ... CX2 X2 ... ... ... CXr X2 ... CX1 Xr CX2 Xr ... CXr Xr , C+(S) = C * _ CT ( S ) Cr (S) 1 Cr (S) J , Cr( S ) = [ Cx0 x 1 ( S ) Cx0 x 2 ( S ) ... Cx0xr (S) f+ = — — f 2 ’ H+ = ——— H2 . И наконец, числовые характеристики вектора ZN найдем из следующих систем ОДУ: В связи с тем, что вектор mr(s) и мат-рнпа Cr ( s ) являются оно ками вектора m+ ( s ) и матрицы C+(s) соответственно, достаточно вычислить только последние, а затем выбрать их необходимые элементы. Из предыдущих рассуждений и из соответствующих соотношений [21] следует, что m N(S) = (рN + QN)•m N(S) + f N, CN ( s ) = (рN + Q N) •cN ( s )+ _i_ 17Р + р +) r+ ] T_i_р + р+т + LIPN+ Qn) • CN(S) +HN •HN m N(0) = m N -1(0) mxN-1 (т) cN (0) = [ cN -1(0) CN -1( т ) CN -1( т) cxn -1 xn -1 ( т ) CN-1(S) = [CN-11 x0 (S) cxn- 1 x0 (S) cxn- 1 x 1 (S) ... cxn- 1 xn-2 (S)] , где — P + N -[ — PN , Q N - [ QN , — f + N = fN HN - .—. 0 HN 4. Результаты расчетов Представленными в предыдущих секциях методы были применены для анализа ря да стохастических систем различных порядков и форм запаздывания. Далее символом "I" отмечается ссылка на все, относящееся к методу Монте-Карло, литерами "II" - к схе-ие МШРФП. Пример 1°. Изучим случайный переходный режим, описываемый стохастическим уравнением пантографа X(t) - aX(t) + bX(pt) + cW(t), 0 < t ^ T, X(0) - X0 (a. b. c. p = cc)iist. 0 < p < 1). в системе e неограниченной памятью. Здесь т — t — pt — (1 —p) t ^ 0. Известно [22], что сильное решение уравнения (7) существует и единственно, а его детерминированный аналог применяется для описания многих явлений, например, динамики токоснимающего устройства электровоза и др. Заметим, что pt ^ 0 щ:ш t ^ 0. а сле довательно, начальное множество для решения рассматриваемого уравнения сводится к единственной точке t — 0 (t* — 0). Программа, разработанная на основе алгоритма II, на каждом шаге в символьном виде генерировала соответствующие ОДУ для элементов вектора математических ожиданий и матрицы ковариаций, а также требуемые начальные условия. Для численного интегрирования этой системы ОДУ использовалась стандартная процедура NDSolve пакета Mathematica. В процессе проведения расчетов использовались следующие значения параметров задачи: ti - 0.0001, tii - 0.005, T - 1.5, c - 0. 125, L - 2000, m0- 5.0, C0- 0.25. Результаты этих расчетов приведены на рис.1 (математические ожидания тх) и 2 (соответствующие дисперсии Dx). Кривые, обозначенные цифрами 1 и 2, соответствуют следующим значениям параметров a, Ъ, p: 1 — a - — 2. b - — 4. p - 0.5: 2 — a - — 2. b - — 4, p - 0.1. Здесь и далее непрерывные и штриховые линии отображают результаты расчетов по алгоритмам I и II соответственно. На рис.1 штрих-пунктирные линии соответствуют приближенным решениям задач для тх (t), полученным с помощью разложения неизвестной функции в ряд Тейлора. Несложно увидеть, что все эти результаты отличаются незначительно. Пример 2°. Уравнения второй из представленных систем выглядели так: X( t) +2 а 1 X(t) + 2 а 2 X( t — т1)+ + в 1 X(t)+ в2 X(t — т2)- yW(t), t> 0; XX(t) - 0, t< 0; m(t*)- m*, C(t*)- C*, где ai, в^ Y ^ постоянные. На рис.3, 4 и 5, 6 изображено поведение компонент вектора математических ожиданий и ковариационной матрицы для фазового вектора X(t) - Рис.4 Рис.6 {X 1 ,Х2}T = {X, X}T при следующих 'значениях параметров: а 1 =0.125, а 2 = - 0.1, в 1 =4, в 2 = 1, Y = 0. 1, ti = п/2000, L = 1000, T = 10 п, т* 0.25 0 0 0. 16 Рисунки слева соответствуют случаю, когда т1 (t) = 0.5 sin22x, тг(t) = 0.5 cos22x, а справа - т1 (t) = 0.5 sin24x, тг(t) = 0.5 cos24x. При этом на рис.З и 4 математические ожидания Xi(t) и X2 (t) отмечены цифрами 1 и 2, а на рис.5 и 6 цифры 1, 2 и 3 указывают на функции Cii (t), C12(t) и C22(t) соответственно. Пример 3°. Последние из представленных резулвтатов касаются двойной системы ван дер Поля. В отличие от классической формы в рассматриваемых уравнениях присутствуют белые шумы и периодические переменные запаздывания в перекрестных термах: Y. (t) + 2 ai [Y2(t) - 1] Yi (t) + w2Yi (t) = = ei Yз—i (t - тз—i) + Yi Wi (t), t> 0; Y.(t )=0, t< 0, i = 1, 2; m (t* )= m*, C (t* )= C *. На рис.7 и 8 на фазовой плоскости изображены траектории математических ожиданий случайных векторов {Y[(t),Y[(t)} и {Y2(t),Y2(t)} соответственно. При этом параметры задачи имели следующие значения: а 1 = 0.5, а 2 = 0.6, w 1 = 2, w 2 = 1, в i = - 0.5, в 2 = — 0.8, Y1 = 0.1, Y 2 = 0.2, т1(t) = 0.5 cos22x, т2(t) = 0.5 sin22x, L = 1000, T = 12 п, т= 0 п/1000, 0 ' 1 /16 0 ∗ C= 0 1 / 25 0 0 0 0 1 / 36 0 ’ 0 0 0 1 /25 _ m* = [0 1 0 1.5]T . Рис. 7 Рис.8 Заключение В работе представлена численная схема исследования нелинейных стохастических систем с переменными запаздываниями. В отличие от известных методов изложенная схема не предполагает предварительного изменения уравнений исследуемого объекта с целью исключения запаздывания или разработки сложных специальных интеграторов. Итоги статистической обработки результатов моделирования для линейных систем с кусочно-постоянными запаздываниями сравнивались с первыми моментными функциями, полученными с помощью схемы МШРФП. Анализ показал удовлетворительное совпадение результатов, полученных разными методами, только при очень мелкой шаге т, что при использовании второго метода приводило к значительному увеличению расчетного времени и объема оперативной памяти.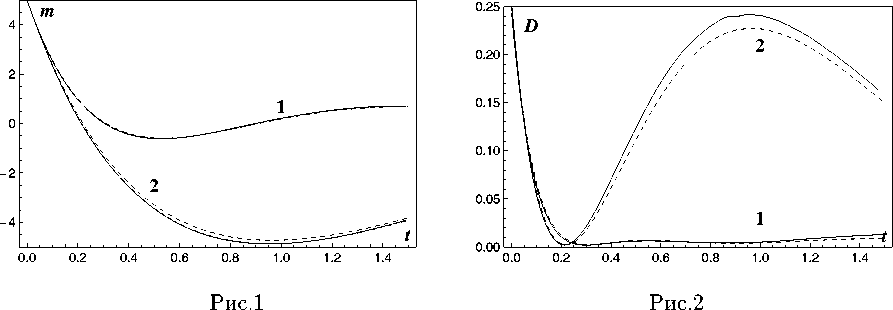
Список литературы Моделирование стохастических систем дифференциальных уравнений с переменными запаздываниями
- Эльсгольц Л.Э., Норкин СБ. Введение в теорию дифференциальных уравнений с отклоняющим аргументом. М.: Наука, 1971. 296 с.
- Системы автоматического управления с запаздыванием: учеб. пособие/Ю.Ю.Громов, Н.А.Земской, А.В.Лагутин и др. Тамбов: Изд-во ТГТУ, 2007. 76 с.
- Хейл Дж. Теория функционально-дифференциальных уравнений. М.: Мир, 1984. 421 с.
- Insperger Т., St ер an С Semi-discretization for time-delay systems: Stability and engineering applications. New York: Springer Science+Business Media, LLC, 2011. XIX, 404 p.
- Bellen A., Zennaro M. Numerical methods for delay differential equations. Oxford Univ. Press, 2005. 412 p.
- Шампайн Л.Ф., Гладвел И., Томпсон С Решение обыкновенных дифференциальных уравнений с использованием MAT-LAB: учеб. пособие. СПб.: Изд-во "Лань", 2009. 304 с.
- Рубаник В. П. Колебания сложных квазилинейных систем с запаздыванием. Минск: Изд-во "'Университетское,!, 1985. 143 с.
- Царьков Е.Ф. Случайные возмущения дйфференциально-функциональных уравнений. Рига: Зииатие, 1989. 421 с.
- Черпоусько Ф.Л., Колмаповский В.Б. Оптимальное управление при случайных возмущениях. М.: Наука, 1978. 352 с.
- Chang М.-Н. Stochastic control of systems and applications of hereditary. New York: Springer Science-fBusiness Media, LLC, 2008. X, 174 p.
- Разевиг В.Д. Корреляционный анализ систем с запаздыванием//Автоматика и телемеханика, 1973. №9. С.42-48.
- Kalos М.Н., Whitlock P.A. Monte Carlo methods. Weinheim: Wiley-VCH Vcrlag. 2004. 195 p.
- Мильштейп Т.Н. Численное интегрирование стохастических дифференциальных уравнений. Свердловск: Изд-во Урал, ун-та, 1988, 224 с.
- Кузнецов Д.Ф. Стохастические дифференциальные уравнения: теория и практика численного решения. 3-е изд., испр. и доп. СПб.: Изд-во Политехи, ун-та, 2009. 800 с
- Kloeden Р.E., Platen Е. Numerical solution of stochastic differential equations. Springer-Verlag, 1995. XXXV. 632 p.
- Кushner H.J. Numerical methods for controlled stochastic delay systems. Boston: Birkhauser, 2008. 295 p.
- Baker C.T.H., Buchwar E. Introduction to the numerical analysis of stochastic delay differential equations//Numerical analysisreport № 345 (revised). Univ. of Manchester, 2000. 25 p.
- Garcia-Palacios, Lazaro E.G. Lange-vin-dynamics study of the dynamical properties of small magnetic particles//Phys. Rev. B. 1998. Vol.58, № 22. P. 14937-14958.
- Полосков И.Е. К анализу линейных стохастических систем с кусочно-постоянными запаздываниями//Вести. Перм. унта. Сер. Математика, Механика, Информатика, 2011. Вып.2 (5). С.76-83.
- Wolfram S. The Mathernatica Book: 5th ed. Champaign, II: Wolfram Media, 2003. 1488 p.
- Маланин В.В., Полосков И.Е. Методы и практика анализа, случайных процессов в динамических системах: учеб. пособие. Ижевск: РХД, 2005. 296 с.
- Baker С.Т.Н., Buckwar Е. Continuous 0-methods for the stochastic pantograph equation//Electronic Transactions on Numerical Analysis. 2000. Vol.11. P.131-151.


