Моделирование течения воздуха в упруго-деформируемой пористой среде, аппроксимирующей легкие человека: алгоритм реализации и анализ результатов применения модели
Автор: Трусов П.В., Зайцева Н.В., Цинкер М.Ю., Нурисламов В.В.
Журнал: Вычислительная механика сплошных сред @journal-icmm
Статья в выпуске: 3 т.17, 2024 года.
Бесплатный доступ
Работа посвящена вопросам реализации разработанной авторами математической модели дыхательной системы человека, предназначенной для прогнозирования возникновения патологий органов дыхания, обусловленных негативным воздействием загрязняющих компонентов атмосферного воздуха. Предложенная модель описывает легкие как упруго-деформируемую насыщенную двухфазную пористую среду, испытывающую большие градиенты перемещений. Поскольку аналитическое решение поставленной существенно нелинейной задачи представляется нереализуемым, для решения предлагается прибегать к численным методам с пошаговыми процедурами. Предложен алгоритм решения связанной задачи фильтрации воздуха в упруго-деформируемой пористой среде. Численное решение нелинейной подзадачи деформирования двухфазной среды легких осуществляется методом конечных элементов, подзадачи фильтрации - методом конечных объемов. Для реализации алгоритма разработан комплекс программ (на языке C++) с применением технологий параллельных вычислений. На основе томографических снимков легких, получаемых с помощью интерактивного программного продукта ITK-SNAP, выполняется восстановление трехмерной формы легких. С использованием пакета ANSYS ICEM CFD строится объемная конечно-элементная сетка. Численное моделирование течения воздуха в легких человека производится для персонализированной трехмерной геометрии. Представлены поля давления газовой фазы в легких человека в различные моменты дыхательного цикла. Разработанную модель в дальнейшем планируется рассматривать как инструмент для определения зон риска развития патологий органов дыхания, обусловленных негативным воздействием аэрогенных факторов среды обитания.
Легкие человека, двухфазная упруго-деформируемая насыщенная пористая среда, геометрическая нелинейность, фильтрация воздуха, алгоритм реализации, численное моделирование, метод конечных элементов, метод конечных объемов
Короткий адрес: https://sciup.org/143183411
IDR: 143183411 | DOI: 10.7242/1999-6691/2024.17.3.28
Текст научной статьи Моделирование течения воздуха в упруго-деформируемой пористой среде, аппроксимирующей легкие человека: алгоритм реализации и анализ результатов применения модели
Многочисленными отечественными и зарубежными исследованиями доказано негативное влияние неблагополучной санитарно-гигиенической обстановки на состояние здоровья человека, в том числе на дыхательную систему [1 –3] . Существующие методы медицинской диагностики [4, 5] предоставляют возможность определять состояние пациента на момент обследования, но они не предназначены для получения прогнозных оценок, в том числе влияния вредных факторов. Прогнозные оценки изменения состояния здоровья населения в зависимости от различных воздействий окружающей среды, которые не всегда удается воспроизвести в натурных испытаниях (например, при выбросах загрязняющих веществ с концентрацией, существенно превышающей допустимую), позволяет сделать математическое моделирование. На протяжении нескольких лет авторами статьи ведется работа по созданию математической модели дыхательной системы человека, предназначенной в том числе для расчета объема поступления ингаляционным путем загрязняющих химических веществ из атмосферного воздуха в организм человека и последующего прогнозирования возникновения патологий органов дыхания, обусловленных негативным воздействием на них [6] .
При исследовании течения воздушной смеси в дыхательной системе широкое распространение получили уравнения газовой динамики [7, 8] , которые с приемлемой точностью описывают процессы в верхних и крупных нижних воздухоносных путях человека. Нижние воздухоносные пути представляют собой разветвленную сеть каналов. При увеличении числа генераций ветвления дыхательных путей возникают сложности как с построением реальной геометрии отдельных каналов и альвеол (в легких взрослого человека содержится около 600–700 млн альвеол, а также соединяющих их каналов [9] ), так и с резко возрастающими требованиями к вычислительным мощностям. Другим подходом к изучению движения воздуха в легких человека является их рассмотрение в виде
Статья опубликована в открытом доступе по лицензии CC BY 4.0
насыщенной пористой среды [6, 10 –13] ; движение воздуха через деформируемую пористую среду моделируется с привлечением теории фильтрации [14, 15] .
В разрабатываемой авторами математической модели биомеханика дыхания человека считается совокупностью взаимосвязанных процессов: 1) течения воздуха в недеформируемой воздухопроводящей зоне (воздухоносных путях) (оно подробно обсуждается в предыдущих работах авторов [6, 16, 17] ); 2) течения воздуха в упруго-деформируемой респираторной зоне (легких человека) [12, 13] . Последнее служит предметом настоящего исследования.
В предыдущей статье авторов [13] приведена математическая формулировка модели течения воздуха в легких человека, аппроксимированных двухфазной насыщенной пористой средой, одна из фаз которой — деформируемый скелет среды (легочная ткань), вторая фаза — газ, заполняющий поровое пространство; представлены разрешающие соотношения, необходимые для решения задачи. Легкие человека в процессе дыхания испытывают большие градиенты перемещений (компоненты которых по результатам предварительных расчетов достигают в некоторых подобластях, особенно в примыкающих к диафрагме и грудной клетке, 90% при спокойном дыхании), вследствие чего рассматриваемая задача относится к классу геометрически нелинейных связанных проблем. Получить ее аналитическое решение для двухфазной пористой среды, испытывающей большие перемещения, и фильтрации газа в ней не представляется возможным. В связи с этим предлагается прибегнуть к численным методам, содержащим пошаговые процедуры.
Численное решение нелинейной подзадачи деформирования двухфазной среды легких предлагается осуществлять методом конечных элементов (МКЭ) [18] , подзадачу фильтрации (относительное течения воздуха в деформируемой пористой среде легких) решать методом конечных (контрольных) объемов (МКО), который хорошо зарекомендовал себя при реализации задач механики жидкости и газа [19, 20] . Достоинством МКО является выполнение законов сохранения как на глобальном, таки локальном уровнях. Для каждого контрольного объема (КО) гарантируется соблюдение баланса полного потока, что является дополнительным плюсом при рассмотрении задач гидроаэродинамики, уравнений переноса. В предложенном алгоритме метод конечных объемов участвует только в расчете просачивания воздуха (обмена массой между соседними КЭ), входные данные (величины давления в элементах) получены с применением МКЭ. При этом в данной работе использованы симплекс-элементы; давление во всех элементах в каждый момент времени однородно. При решении уравнения Дарси (описывающего фильтрацию газа) с помощью МКЭ потребовался бы повышенный порядок аппроксимации (для определения градиента давления). Это повлекло бы увеличение объема вычислительных ресурсов. Решение же уравнения Дарси МКЭ с привлечением симплекс-элементов нуждается в создании дополнительной процедуры, которая и реализуется в представленной работе МКО.
Исследование процесса течения воздуха в дыхательной системе человека производится численно для ее индивидуальной трехмерной геометрии, восстановленной на основе данных компьютерной томографии [13, 16, 17, 21] .
-
2. Восстановление трехмерной формы легких, задание закона движения стенок
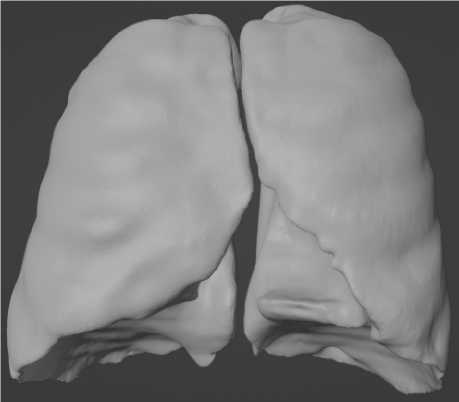
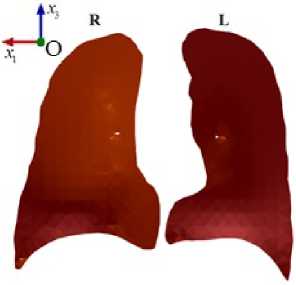
Реконструкция реальной трехмерной формы легких человека выполнена исходя из данных компьютерной томографии, взятых из открытой базы данных I-ELCAP (International Early Lung Cancer Action Program) [22] . Обработка исходных двумерных изображений (томографических снимков в формате DICOM, размещенных в файлах с расширением dcm), процедура сегментации и восстановление трехмерной формы осуществлены посредством программного продукта с открытым доступом ITK-SNAP [23] . Полученная после применения процедуры сегментации трехмерная форма легких представляет собой поверхностную сетку, информация о которой хранится как список составляющих ее треугольных граней и нормалей к ним в файле формата stl. Сетка обработана в графическом редакторе Blender. В результате обработки построены поверхности бронхов (5 поколений дерева бронхов) и внешние поверхности легких, а также выполнено сглаживание этих поверхностей. На рисунке 1 представлена трехмерная форма легких до и после сглаживания.
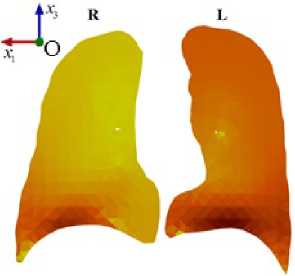
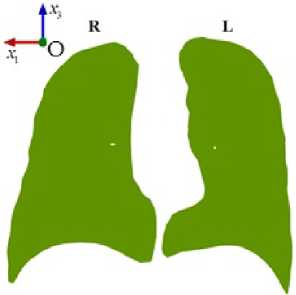
При обработке в редакторе Blender из внутренней области легких (Рис. 1б ) исключены внутрилегочные участки бронхов (используемые при исследовании течения воздуха в воздухопроводящей зоне [17] ). На основе поверхностной сетки легких в комплексе ANSYS (модуль ICEM CFD) сгенерирована объемная конечно-элементная сетка, аппроксимирующая деформируемую насыщенную пористую среду легких для изучения фильтрации воздуха. Эта сетка представлена на рисунке 2. Здесь показаны области и границы, учитываемые в разрабатываемой модели легких человека. Символом Ω обозначена внутренность области легких, рассматриваемая как двухфазная
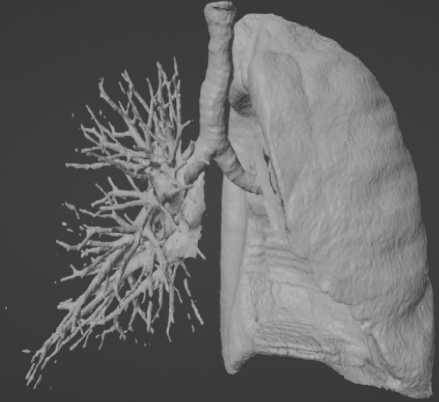
Рис. 1. Восстановленная трехмерная форма легких до обработки ( а ), после обработки сглаживанием ( б )
( a )
пористая среда; Γ L — стенки легких; Γ AW/L — границы выходов из бронхов, являющиеся входами, через которые в легкие воздух поступает во время вдоха и выходит из легких во время выдоха. В рассматриваемой геометрии присутствует 31 вход в легкие из системы бронхов (14 входов в левом легком и 17 в правом).
При исследовании движения воздуха в деформируемой пористой среде легких на входах в легкие (границах Γ AW/L ) задаются силовые граничные условия для газовой фазы (для подзадачи фильтрации); трахея и бронхи полагаются достаточно жесткими, в силу чего для подзадачи деформирования пористой среды на границе Γ AW/L считаются известными кинематические условия тривиального вида — равенство нулю всех компонент скоростей перемещений; на стенках легких ( Γ L ) принимаются граничные условия кинематического типа, согласно которым по предписанному закону перемещаются точки каркаса, и условия непроницаемости для газовой фазы.
Легкие находятся в грудной клетке (каждое в своем плевральном мешке). Они соприкасаются снизу с главной дыхательной мышцей — диафрагмой, разделяющей грудную и брюшную полости, по сторонам — со стенкой грудной клетки [9] . Движение воздуха в легких в процессе дыхания (вдох, выдох) обусловлено разностью давления на входах бронхов в легкие и изменяющимся давлением воздуха в самих легких вследствие изменения их объема. Изменение объема легких осуществляется за счет грудного дыхания (расширения/сжатия грудной клетки) и диафрагмального (брюшного) дыхания (опускания/подъема диафрагмы). При этом наибольшее изменение формы (максимальные перемещения) реализуется за счет движения диафрагмы и обеспечивает вентиляцию воздуха в 2/3 объема легких [24, 25] .
Наиболее детальное описание движения стенок легких получено с использованием 4D-компьютерной
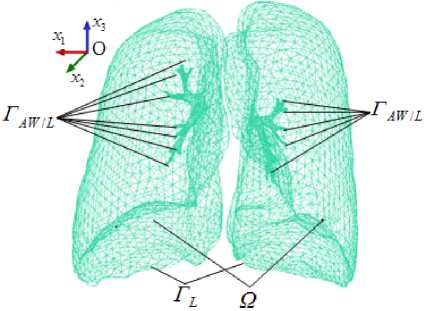
Рис. 2. Конечно-элементная сетка легких для исследуемой области, заполненной двухфазной пористой средой (вид спереди)
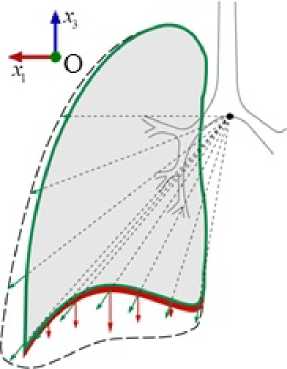
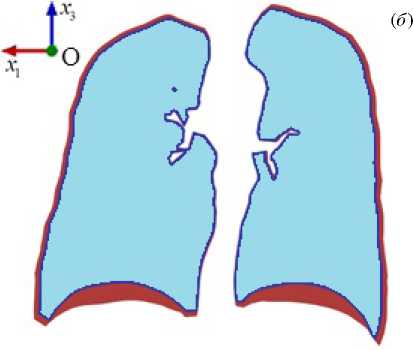
Рис. 3. Схематичное изображение изменения формы легких в процессе дыхания (на вдохе контур легкого обозначен пунктирной линией, на выдохе — сплошной), а также приложения граничных условий ( а ); рассчитанная геометрия легких во фронтальной плоскости в момент максимального вдоха и в начальном состоянии ( б )
томографии [26 –29] . Название происходит от добавления времени (как четвертого измерения) к традиционной трехмерной томографии (4D = 3D+ 1). К сожалению, авторам не удалось найти в открытом доступе данные об изменении 3-мерной геометрии легких в разные моменты дыхательного цикла. Стенки легких в процессе дыхания имеют сложный характер движения, для описания которого необходимо создание подмодели костно-мышечной системы и диафрагмы, окружающих дыхательные органы человека. В связи с этим в данной работе предлагается в первом приближении использовать упрощенные граничные условия, имеющиеся в обзорах результатов медицинских исследований, обеспечивающие интегральные характеристики — изменение общего объема воздуха в легких, смещение диафрагмы и грудной клетки.
В качестве начального состояния дыхательного цикла рассмотрим момент «конец выдоха–переход к вдоху». Для этого момента полагается, что скорости движения частиц воздуха равны нулю, перепад давления в легких и воздухоносных путях (на входах в легкие) отсутствует, давление воздуха в легких аналогично атмосферному). В процессе дыхания легкие расширяются в горизонтальной (0x 1 x 2 ) и вертикальной (фронтальной) (0x 1 x 3 ) плоскостях (Рис. 3а ). При спокойном дыхании расширение (экскурсия) грудной клетки — разность между показателями ее окружности на вдохе и выдохе, составляет 2-3 см [30] , на максимальном вдохе и выдохе—7 ^ 8.5см [30] , 6 ^ 8 см [31] . В зависимости от вертикальной координаты (x 3 ) экскурсия грудной клетки (и, соответственно, легких) различается. В области вершины легкого она наименьшая, по мере приближении к основанию легких степень их расширения увеличивается. На уровне подмышечной впадины периметр грудной клетки изменяется в среднем на 3.52 см у мужчин и на 3.19 см у женщин; на уровне 3–4-го межреберного пространства, соответственно полу, — на 4.02 см и на 3.71 см; в области нижнего края грудины (на уровне мечевидного отростка) — на 4.52 см и на 4.12 см [32] . Средние показатели периметра грудной клетки зависят от пола, возраста, конституции человека: у мужчин 18 лет это 90.20 ± 5.24 см (среднее ± стандартное отклонение — M ± SD), 26-30 лет — 92.24 ± 4.94, у женщин 18 лет — 84.08 ± 4.38 см, 26-30 лет — 85.32 ± 4.72 [33] . Исходя из проведенных оценок степень расширения грудной клетки (и легких соответственно) при спокойном дыхании оценивается в 2–4.5% от исходного состояния.
Нижние границы легких, соприкасающиеся с диафрагмой, имеют форму купола. В процессе дыхания диафрагма (а также основание легкого) опускается, вершина купола испытывает при этом наибольшие смещения. Точки, принадлежащие одновременно нижним и боковым границам, проходят наименьшие расстояния. В конце вдоха контуры оснований легких уплощаются.
При спокойном дыхании диафрагма, по разным источникам, смещается на 1 см [34] или 0.5 ^ 2 см [35] , при форсированном дыхании амплитуда ее движения может достигать 10 см [34] или 7 ^ 8 см [35] . В соответствии с данными МРТ из [36] , средняя амплитуда движения диафрагмы при спокойном дыхании составила 27.3 ± 10.2 мм (M ± SD). В работе [37] приведены результаты измерений, полученные с использованием цифровой рентгенографии, согласно которым амплитуда перемещения правого купола диафрагмы достигала 25.1 ± 6.8 мм, левого купола — 30.6 ± 8.2 мм.
В работах [10, 11, 38], посвященных численному моделированию процессов в легких, рассмотрен синусоидальный закон движения диафрагмы, в [10, 11] максимальное смещение в основании легких принималось равным 1.5 см. В [39] амплитуда смещения опорных точек, лежащих в основании правого легкого, составляла 12.7±6.1 мм (M±SD), в основании левого легкого — 16.5±4.5 мм; максимальное смещение достигало 24 мм.
При решении задачи в настоящей работе предполагаются известными кинематические граничные условия в скоростях для точек стенок легких. Для всех точек задаются смещения вдоль прямых, соединяющих точки границы и «центр» легких (точку, лежащую посредине между входами главных бронхов в легкие человека). При этом чем большее расстояние от точки стенки до «центра», тем больше амплитуда перемещения точки в процессе дыхания. Коэффициент, характеризующий скорость смещения стенок легких из исходного состояния, определяется исходя из оценки степени расширения грудной клетки (и легких). Чтобы принять во внимание более выраженное и неоднородное смещение точек в областях легких, прилегающих в процессе дыхания к диафрагме, используется дополнительное условие, учитывающее неравномерность смещения точек по вертикальной координате (x 3 ) в зависимости от их удаленности от вершины купола.
При взятом в качестве начального отсчетного состояния дыхательного цикла моменте «конец выдоха–переход к вдоху» принимается периодический закон движения стенок; период дыхания при обычном спокойном дыхании равен t * =4 с [34] .
Кинематические граничные условия для точек, принадлежащих боковой поверхности легкого, записываются в виде:
V s = (2n/t * )(5 | 1 | /2) 1 n sin(2nt/t * ), (1)
где V s — вектор их скорости, l—вектор длиной 1 1 | , соединяющий «центр» и точку поверхности легкого в начальный момент времени, l n — нормированный вектор, направленный вдоль l , δ — отношение максимального смещения (в направлении l n ) точки на поверхности легкого от значения | l | в начальном положении, δ | l | — максимальное смещение точки поверхности легкого от начальной точки в процессе дыхания, 2n/t * — циклическая частота.
Кинематические граничные условия в скоростях для точек, принадлежащих основанию легких, принимаются следующими:
V d = V s + V d . (2)
Здесь вектор V d описывает скорость неравномерного смещения по вертикальной координате, [м/с]. Вектор V d имеет только вертикальную ненулевую компоненту v * 3 (v * 1 = v * 2 = 0); для каждого легкого она своя и определяется из соотношения:
* = (-(d ■ l(-Cn/t*)si„(2n(/(*), (3) I (max(d)) I где C — смещение точек вершины купола основания легкого без учета их смещения по вертикальной координате за счет первого слагаемого из правой части (2) за время t*/2 = 2 с (при расчетах в качестве C используются величины: CL для левого легкого, CR для правого), d — расстояние от точки в основании легкого до ближайшей точки контура, одновременно принадлежащего как границе основания, так и боковой стенке соответствующего легкого в начальный момент времени.
Максимальная удаленность от контура основания легкого (max(d)) имеет место в точке, являющейся вершиной купола диафрагмы (прилегающей к основанию легкого). Согласно соотношению (3) при d = max(d) скорость смещения точек во фронтальной плоскости максимальна, за 2 с вдоха вершина купола диафрагмы смещается на C . Вертикальная компонента скоростей точек контура основания легкого (d = 0) равна нулю; скорость смещения точек основания легкого определяется только за счет первого слагаемого в правой части соотношения (2) .
Результаты выполненного обзора медицинских исследований и осуществленных предварительных расчетов позволили идентифицировать параметры, входящие в закон движения стенок легких, используемый для задания граничных условий. Получены следующие значения: 5 = 0.0191, C L =0.013 м, C R = 0.012 м. При этих параметрах максимальное смещение по вертикальной координате основания левого легкого достигает 0.0155 м, правого легкого — 0.0146 м; объем газовой фазы в легких изменяется на 0.79 л (0.00079 м 3 ). Приведенные параметры соответствуют известным физиологическим данным для спокойного дыхания взрослого человека.
-
3. Алгоритм решения связанной задачи
Связанная задача фильтрации воздуха в упруго-деформируемой пористой среде является нелинейной. Ее реализация осуществляется в виде пошаговой (по времени) процедуры при достаточно малых временных шагах.
Последовательно решаются подзадачи расчета параметров деформирования двухфазной пористой среды (с использованием МКЭ) и относительного течения воздуха в пористой среде (с использованием МКО).
На текущем ( n - м) шаге рассматривается отрезок времени [t n - i ,t n ]. Решение в скоростях отыскивается при времени t n -1 и граничных условиях (в скоростях) для этого же момента t n -1 при значениях переменных с конца предыдущего — (п — 1) - го, шага. Обсуждаемая задача сводится к двум подзадачам: подзадаче деформирования двухфазной среды в скоростях и подзадаче фильтрации (относительного течения воздуха в деформируемой пористой среде легких) с использованием результатов расчета давления, полученных при решении первой подзадачи. По определенным в момент t n -1 скоростям изменения искомых параметров путем интегрирования вычисляются значения параметров в момент t n ; для интегрирования применяется явная схема Эйлера. Процессы деформирования пористой среды и фильтрации воздуха в ней различаются по интенсивности и скорости распространения в пространстве, в связи с чем при решении подзадачи фильтрации полагается переменный (более мелкий) временной шаг; на произвольном n-м шаге решения подзадачи деформирования производится K n > 1 решений подзадачи фильтрации.
Реализация решения совместной задачи рассматривается в условно неподвижной лабораторной (декартовой) системе координат (ЛСК), связанной с позвоночником. В работе используется текущий лагранжев подход к моделированию: на каждом временном шаге решения задачи лагранжевы координаты переопределяются (полагаются совпадающим с координатами введенной условно неподвижной декартовой ортогональной ЛСК).
Скорости частиц двухфазной среды находятся через скорости движения частиц каждой из фаз как среднемассовая скорость смеси. В силу того, что масса газа, содержащегося в объеме двухфазной среды легких, пренебрежимо мала по сравнению с массой их твердого каркаса, скорость двухфазной среды можно считать совпадающей со скоростью твердой фазы ( v = v s ). Скорость движения частиц воздуха в рассматриваемой точке можно выразить в виде суммы скоростей «переносного» движения (смещения частиц вместе с деформируемой твердой фазой во введенной лабораторной системе координат) и «относительного» движения, обусловленного просачиванием газа через твердый каркас.
Разрешающие соотношения МКЭ для подзадачи деформирован ия д вухфазной пористой среды легких человека, аппроксимированной сеткой из m тетраэдральных элементов (m =1 ,M), получены в [13] (см. формулу (29)). В этом соотношении суммирование по элементам осуществляется для компонент матриц с их глобальными номерами:
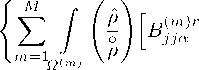
17R(m)q , R(m)r,,A, R(m)q । R(m)r,,A, R(m)q 3 ZB kke + B jia ^ f s B jie + B jia IB^B je
( m ) r 2 ' rmmqq, o(m)r 2 x o(m)q 1 J p(m) L(m)e , B jja g ^Y s B kke + B jia 3 ^ j B kke Jd^ (v q +
+
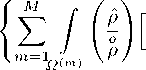
R(m)r 1ft R(m)q B jia 2 S kj B ike
,(m)r 1^ Tm(m)q_ R(m)r 1 q Tm(m)q
’ jia 2 S kj B kie B jia 2 S ik B kje +
1 d(m)r 1 q D(m)q D(m)r V D(m)q 1лo(m) СЛ1(т)в_|_ + Bjia ^ Sik Bjke ~Bjia ^kj Bike Jd^v
{ Mr
X X I P E- \ Го(т)г /О C D(m)q TD(m)r ,Q Q R(m)ql z7 o(m) l^(m)e_|_
I \ o I LBjia QiplkSPj Bike Bjia QpjlkSip Bike J d^ fvq m=b(m) PP'
M Γ
X ( m ) r ( m ) q ( m ) q
+ L / N ia —T i B ^kkU +B lke n k n l T i
(m=1
(m)
Γ AW/L
\^L]mr==| E / Nm[T^rm/A.
J m = l (m)>
Γ AW/L
В (4) приняты обозначения: индексы в виде греческих букв α и β — номера узлов, в виде латинских букв — координатные оси; Nim — функции формы (Na) (re) = 0 при a = в; Nim(re) = ^i; i,j = 1,3); Bjm) (r) = dNjem' (r)/dxi — производные функций формы; V^m)13 — вектор узловых скоростей; компоненты скоростей перемещений внутри элемента и компоненты градиента вектора скорости со скоростям перемещений в узлах связаны формулами i(m) = Nim4 (r)v(m)e, vj™) = dvjm / dxl = В^в4 (r^v^m)13; p/p — отношение плотностей двухфазной среды в текущей и отсчетной конфигурациях; Z — переменная, введенная в описание связи скорости изменения среднего напряжения в терминах тензора напряжений Кирхгоффа двухфазной среды (Σav) со скоростью изменения объема двухфазной среды (первым инвариантом тензора деформации скорости D) с учетом взаимодействия газа и легочной ткани: Sav = Ii(D)Z [12, 13,40]; j — второй параметр Ламе твердой фазы; is — объемная доля твердой фазы; Σij — компоненты взвешенного тензора напряжений Кирхгоффа двухфазной среды лл
i
л_
в актуальной конфигурации; S kj — компоненты девиатора тензора напряжений Кирхгоффа твердой фазы; Q iplk — компоненты тензора четвертого ранга Q , входящего в определение логарифмического спина [41, 42] ; П (m) — подобласть, занимаемая m-м конечным элементом двухфазной пористой среды легких; r AW/L — границы выходов из воздухоносных путей, которые одновременно служат входами для воздуха в легкие человека (Рис. 2) ; T i — компоненты вектора поверхностных сил (вектора напряжений); n k — компоненты вектора нормали.
Соотношение, являющееся основным в МКО для определения плотности газовой фазы в элементе легких — КО (его вывод представлен в [13] , см. выражение (32)), имеет вид:
( a (n - 1) (n - 1) (n - 1) \
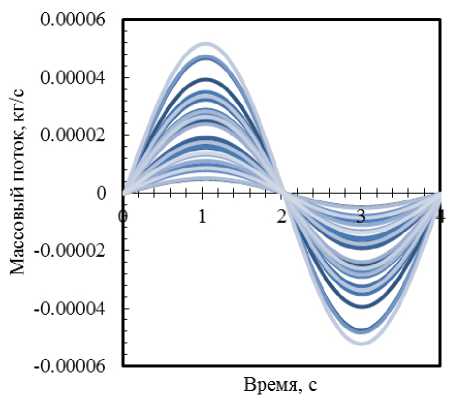
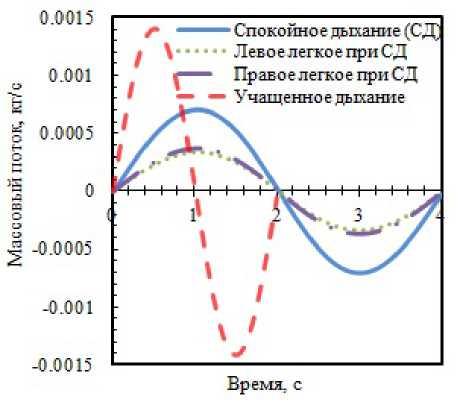
, (n-1) k(H) pfA(a) -pfC eCA^X (n-1)s(n-1) At , (n-1)™ pf -f • |e(n-1)| |e В качестве КО используются те же КЭ, которые применяются для решения подзадачи деформации пористой среды легких. На основе соотношения (5) определяется изменение плотности газовой фазы в КО (КЭ) за счет изменения их объема вследствие поступления/оттока массы (между соседними элементами или через границы (грани) ΓAW/L, являющиеся выходами из воздухоносных путей и одновременно входами в легкие), обусловленное градиентом давления газовой фазы. Подзадачи деформирования двухфазной пористой среды легких и фильтрации воздуха в пористой среде взаимосвязаны между собой. Поля напряжений и перемещений, установленные из решения подзадачи деформирования, применяются далее для решения подзадачи фильтрации. Давление воздушной фазы зависит от изменения двух составляющих: объема легких в процессе деформирования и значения плотности воздушной фазы (производные по времени давления и плотности прямо пропорциональны). Переопределяемое при решении подзадачи фильтрации давление необходимо для решения подзадачи деформирования пористой среды на следующем временном шаге (входит в соотношение для расчета переменной Z, описывающей связь скорости изменения среднего напряжения двухфазной среды легких со скоростью изменения объема двухфазной среды, учитывающей взаимодействие газа и легочной ткани [13]). Таким образом, в процессе решения выполняется обмен данными между подзадачами. Как показали результаты предварительных расчетов, для решения подзадачи фильтрации требуются меньшие шаги по времени (в дополнительном цикле по времени), чем для реализации подзадачи деформирования. Использование более мелких шагов в подзадаче фильтрации позволяет избежать скачков давления газовой фазы в элементах, связанных с изменением объема, повысить устойчивость и сходимость решения (что особенно заметно при мелкой конечно-элементной сетке). При этом в подзадаче фильтрации шаг по времени зависит от величины перепада давления газовой фазы, то есть является переменным. При достижении в подзадаче фильтрации момента времени, соответствующего концу текущего шага решения подзадачи деформации, цикл решения подзадачи фильтрации заканчивается. Алгоритм решения задачи в виде пошаговой процедуры, состоящей из трех этапов, представлен на рисунке 4. Этап I. Постановка подзадачи деформирования двухфазной среды осуществлена в скоростной форме, наиболее подходящей для геометрически нелинейных задач [43], поэтому в момент времени tn-1 n-го шага решается подзадача деформирования двухфазной пористой среды в скоростях с использованием граничных условий в скоростях для момента времени tn-1 и значений переменных с конца (п — 1)-го шага по времени. Определяются вектор узловых скоростей (v(n 1)), скорости изменения компонент тензора напряжения (S( )), тензора Альманси (A( )) и давления газовой фазы за счет изменения объема (pfn 1)) (верхний индекс (п— 1) обозначает их соответствие моменту времени tn-i). Этап II. Решается подзадача фильтрации (для объема V(п 1)), находятся скорости изменения характеристик газовой фазы (pf 1), pf 1)) на момент tn-1и значения параметров (pfn) (п) ~(n)\ , mf , pf ) на момент tn . Этап III. Интегрируются скорости изменения искомых переменных, отвечающие моменту времени tn-1, и вычисляются их значения на момент времени tn для использования на следующем временном шаге (следует заметить, что перед началом первого шага по времени в цикле по времени в подзадаче деформирования задаются условия на момент времени t0, являющиеся начальными на 1-м временном шаге). Начальный момент времени t0. В качестве этого времени, как отмечено ранее, выбран момент перехода от выдоха к вдоху. При этом легочная ткань находится в естественном ненапряженном состоянии, давление газовой фазы в легких и на входе одинаковое и равно атмосферному: pf0)= patm; шаровая составляющая и компоненты девиаторной части (S) тензора напряжений твердой фазы являются нулевыми; взвешенный тензор напряжений Кирхгоффа двухфазной среды определяется шаровой частью, основной вклад в которую вносит давление газа, находящегося в легких (S(0)= Z^I); среднее напряжение взвешенного тензора напряжений Кирхгоффа есть среднее напряжение тензора Коши (Д® = j^V)); среднее напряжение двухфазной среды следует из соотношения, полученного в результате решения вспомогательной задачи о всестороннем сжатии/растяжении представительного объема двухфазной среды в форме шара, заполненного воздухом [40]: ■ . у \ ab(V—Vf) (\/VV pv] — CVfPf (AVf + BV И Л J Здесь aav — среднее напряжение в терминах тензора напряжений Коши двухфазной среды; V, V — объем двухфазной среды в отсчетной и текущей конфигурациях; Vf — объем газовой фазы в текущей конфигурации; A = (2р+3а), B = 4р, C = (6р+3а), а, р — параметры Ламе твердой фазы. Далее, через координаты узлов определяются функции формы [N](0)и их производные [B](0), а также объем V(0)КЭ. Согласно известным экспериментальным данным объемная доля воздуха в легких варьируется от 81 до 87.4% [44–47]; величина пористости (доля газовой фазы) в начальный момент времени принимается равной 0.85 (Yf0)), объемная доля легочной ткани, соответственно, 0.15 (7(0)). На основе информации об объеме элемента и доле газовой фазы находится объем газовой фазы в отсчетной конфигурации, а также объем твердой фазы (легочной ткани), который в процессе дыхательного цикла меняется несущественно [48] и потому полагается постоянным на всех временных шагах. По заданным параметрам упругости легочной ткани, пористости материала при атмосферном давлении газовой фазы вычисляется значение Z(0). В начальном состоянии компоненты тензора деформации Альманси (A(0)) нулевые; собственные значения тензоров искажений, характеризующих отношение длин материальных отрезков в актуальной и отсчетной конфигурациях, направленных вдоль главных векторов левой и правой мер искажений pi и pi [43], равняются 1. Компоненты тензора спина, а также тензора четвертого ранга Q, отыскиваемые с использованием собственных значений тензоров искажений, в начальный момент времени являются нулевыми. Рассмотрим детально реализацию алгоритма на произвольном n-м шаге по времени. Полагается, что все параметры (Z, S, S, Q, [B], объемы КЭ (двухфазной среды), объемы и объемные доли фаз) на момент начала данного шага tn-1(конца предыдущего — (п — 1)-го шага) определены (на 1-м временном шаге они известны из начальных условий). На Этапе I алгоритма решается подзадача деформирования двухфазной среды в скоростях. На основе разрешающего соотношения МКЭ (см. (4)) по значениям переменных (Z, S, S, Q, [B]) с конца предыдущего (п — 1)-го шага по времени (для момента времени tn-1) и граничным условиям на начало текущего n-го шага (для момента времени tn-1) формируется система линейных алгебраических уравнений (СЛАУ). В результате ее решения устанавливаются значения компонент вектора среднемассовой скорости двухфазной среды v(n-1)в узлах КЭ сетки (этот вектор, в силу относительной малости удельного веса воздуха, с высокой степенью точности равен вектору скорости частиц твердой фазы; при этом вклад от скорости просачивания воздуха является малым). При реализации разрешающего соотношения (4) в части выполнения силовых граничных условий последний член левой части и правая часть, содержащие интегралы по поверхности, принимаются равными нулю. Рис. 4. Схема алгоритма решения связанной задачи течения воздуха в упруго-деформируемой пористой среде По вычисленным компонентам вектора скорости перемещений двухфазной среды v(n 1) и функций формы [B](n 1) определяются компоненты градиента вектора скорости перемещений двухфазной среды Vv(n-1), вычисляются компоненты тензора деформации скорости D(n-1)= (vv(n 1) +v(n ^V)/2, его первый инвариант I1 (D(n-1)) и компоненты девиатора d(n-1)= D(n-1)— (1/3)I1 ^D(n-1)j I, компоненты тензора вихря W(n-1)= (v(n-1)V — V v(n-1)j.2. Материальная производная тензора напряжений Кирхгоффа с учетом переменных с конца предыдущего — (n— 1)-го, шага по времени (на момент времени tn-1) рассчитывается на основе соотношения: ± (n 1) = I1(D(n-1))Z (n-1)I+2Md(n-1)7(n-1) ^^EnT1) •S(n-1) — S(n-1) ^nT1), где D — тензор деформации скорости двухфазной среды, I — единичный тензор, d — девиатор тензора деформации скорости, 7s — объемная доля твердой фазы, Qlog — логарифмический спин. С использованием градиента вектора скоростей перемещений Vv(n-1)и значения тензора деформации A(n-1)с предыдущего шага по времени определяется скорость изменения тензора Альманси [43]: A(n-1)= 1(7v(n-1)+VvT(n-1)) — (Vv(n-1)•A(n-1)+ A(n-1)•VvT(n-1)). Выше сказано, что давление воздуха зависит от двух составляющих: 1) от изменения объема (результата решения подзадачи деформирования); 2) от перетекания воздуха между КО (результата решения подзадачи фильтрации). Скорость изменения давления газовой фазы за счет изменения объема (обозначаемая как pf 1)) становится известной на Этапе I алгоритма в результате вычисления первого инварианта тензора деформации скорости. Для установления связи pf 1) со скоростью изменения объема используются следующие рассуждения. В процессе движения по воздухоносным путям (включающим в себя носовую полость, глотку, гортань, трахею и 5 поколений дерева бронхов) вдыхаемый воздух нагревается/охлаждается до температуры тела. Полагается, что фильтрация воздуха в пористой среде легких происходит при постоянной температуре. На каждом малом промежутке времени массу газа, находящегося в альвеолах, можно считать постоянной; при изотермических условиях pf Vf = const (или pf pf1 = const). Соотношение для изменения давления газовой фазы в зависимости от изменения объема газовой фазы (или от изменения плотности), вытекающее из закона Бойля–Мариотта, записывается в виде pf /pf = —Vf Vf, или pf /pf = pf /Pf. Первый инвариант тензора деформации скорости определяет скорость изменения объема двухфазной среды: I1 (D) = dV / dV. Изменение объема двухфазной среды обусловлено изменением объема газовой фазы (изменением объема твердой фазы можно пренебречь): ЛЛ VV I1(D) = V « V. Из соотношения (7) следует выражение: Vf /Vf = I1(D) (V /Vf) = I1(D)/7f. Тогда с использованием (6) и (8) скорость изменения давления газовой фазы за счет изменения объема (pf 1)) определяется как pf /pf = I1 (D)/Yf или pfn-1) = —pfn-1)I1(D(n-1))/7fn-1). На Этапе II при реализации подзадачи фильтрации воздуха временной интервал от конца предыдущего/начала текущего среза по времени (момента tn-1) до конца текущего (n-го) шага (на момент tn), равный одному шагу по времени в решении подзадачи деформирования, разбивается на K временных шагов. Введем индекс k для обозначения номера шага по времени в подзадаче фильтрации (к =1 ,К). При k = 1 момент времени соответствует началу шага по времени tn-1 (в подзадаче деформирования), k = K — моменту времени tn; сумма временных шагов подзадачи фильтрации равна временному шагу подзадачи деформирования. На начало шага по времени tn-1 для решения подзадачи с использованием координат узлов (вычисленных при решении подзадачи деформирования двухфазной среды) определяются: координаты центров элементов; векторы, соединяющие центры соседних КО (e^^a))) и расстояние между этими центрами — | eCa(a) |; площади граней — S^n 1) (с привлечением операции векторного произведения) и вектор нормали к общей грани этих КО — п(П-1). D (n-1) I (n-1) I c(n-1) (n-1) ВычисленныечерезкоординатыузловпараметрыecA(a), |eCA(a)|, S(a) , n(a) полагаютсяпостояннымина всех K временных шагах решения подзадачи фильтрации. Таким образом, на n-м временном шаге решения подзадачи деформирования (далее в приведенных соотношениях индекс n, обозначающий шаг по времени, опущен) на основе разрешающего соотношения МКО (5) с использованием начальных и граничных условий для газовой фазы определяется плотность газовой фазы на k-м шаге решения подзадачи фильтрации в КО (давление газовой фазы в КО получено из решения МКЭ задачи деформирования пористой среды): .(k) X pf -z^ (a) (—А-Dk(H) у f Pf (k-1) (k-1) pfA(a) — pfC I e(n-1) eCA(a) (n-1) eCA(a) e(n-1) eCA(a) (n-1) (n-1) ·n S (a) (a) Atk • (n-1)V (n-1) +p (k-1) f Фильтрация воздуха осуществляется только между КО, имеющими общие грани. Через грани КО, принадлежащие границам (стенкам легких) области исследования, фильтрация не осуществляется, тем самым учитывается условие их непроницаемости для газовой фазы. Нулевому значению индекса соответствуют данные на начало шага в решении подзадачи деформирования. По найденной плотности газовой фазы находится масса газа в каждом КО: (k) (n-1) (k) mf = Vf -Pf , и скорость изменения плотности газовой фазы •(k-1) = fMkJl Pf Atk . С использованием данных о скорости изменения плотности газовой фазы вычисляется скорость изменения давления в КО за счет фильтрации газа: •(k-1) pf (k-1) ρf Mf Rθf где pf — скорость изменения давления газовой фазы за счет фильтрации воздуха, R, Q f, Mf — универсальная газовая постоянная, температура и молярная масса газа соответственно. Скорость газовой фазы за счет фильтрации определяется согласно соотношению, следующему из закона Дарси; поток (массовый расход) газовой фазы находится как произведение ее плотности, скорости и площади общей грани между соседними элементами. Путем интегрирования скорости изменения давления газовой фазы за счет фильтрации в каждом КО пересчитывается значение давления газовой фазы на конец текущего шага решения подзадачи фильтрации: tk (k) (k-1) •(k-1) pf = pf ' / pf d^ tk-1 где pf — давление газовой фазы, пересчитанное с учетом вклада фильтрационной составляющей. На первом временном шаге решения подзадачи фильтрации (при k = 1) давление газовой фазы соответствует давлению конца предыдущего/начала текущего шага решения подзадачи деформирования (pf 1) = pf0= p(n 1)). В результате выполнения Этапа II алгоритма (по окончании пошаговой процедуры для фильтрации (tk= tn)) становятся известными параметры газовой фазы на текущем — n-м, временном шаге (на момент tn). На Этапе III устанавливаются значения параметров на момент времени tn (на конец n-го шага) для их использования на следующем шаге. По вычисленному вектору скорости перемещений рассчитываются за временной шаг приращения перемещений u(n)= v(n—1)At и координат узлов x(n)= x(n—1) + v(n-1)4t. По переопреленным координатам находятся функции формы [N](n)и их производные [B](n). По известным координатам узлов пересчитываются объемы (V(n), V^n)) и объемные доли фаз (fl(n), Y(n)). Отношение плотностей двухфазной среды в текущей и отсчетной недеформированной конфигурации О р / Р = V /V в каждом элементе отыскиваются как P(n)/р(0)= V(0)/v(n). (n) По пересчитанным объемам Vfпереопределяется плотность газовой фазы в каждом КО: Pf = m?"/Vf . Далее скорость изменения давления газовой фазы за счет изменения объема (см. формулу (9)) интегрируется, и назначения давления в КЭ: tn (n) ~(n) . I -!-(n —1) 7^ Pf == p? + p? ’d.. tn-1 Путем интегрирования скорости изменения тензора деформации Альманси и суммирования его компонент с их приращениями (в базисе ЛСК), вычисленными на конец предыдущего (начало текущего) шага по времени, tn определяется тензор деформации Альманси на момент времени tn (A(n) = A(n—1) + ^ A( )d£). Для тензора tn-1 деформации Альманси находятся его собственные значения Ai и соответствующие им главные векторы pi. По Ai на основе соотношения (Ai = (1 — 2Ai)—1/2) вычисляются собственные значения правого тензора искажений Ai. С использованием главных векторов pi рассчитываются косинусы углов между ними и базисными векторами ЛСК ki . По вычисленным значениям λi и компонентам матрицы косинусов устанавливаются компоненты тензора четвертого ранга Q(n), а по найденным D(n), W(n), Ai — компоненты тензора логарифмического спина Q^ [13]. Далее выполняется определение переменной Z(n), учитывающей взаимодействие газа и легочной ткани. С помощью интегрирования вычисляется взвешенный тензор напряжений Кирхгоффа двухфазной среды (S(n)= tn s(n—1) + у ±(n—) d^) и его девиатор (S(n)). После этого осуществляется переход на следующий временной шаг. tn-1 Для реализации описанного выше алгоритма, основанного на методах КЭ и КО, авторами разработан программный комплекс (на языке программирования C++ с привлечением библиотеки Eigen). Будучи нелинейной и обладающей значительной вычислительной сложностью, задача решалась с помощью пошаговых процедур. Вычисления производились на многопроцессорных системах с применением технологии параллельных вычислений. Рабочий процессор имел 12 ядер с частотой 3.3 ГГц. Распараллеливание вычислений выполнялось с использованием директив стандарта OpenMP. По тестовым оценкам использование 12 ядер повысило производительность счета почти в 10 раз. Таблица 1 содержит информацию о параметрах, которые применялись для решения задачи фильтрации воздуха в деформируемой пористой среде легких. Для визуализации результатов вычислений на основе разработанного программного комплекса использовался открытый графический кроссплатформенный пакет ParaView [50]. 4. Результаты В результате численного решения согласно предложенному алгоритму связанной задачи течения воздуха в упруго-деформируемой пористой среде легких получено пространственное распределение параметров легочной ткани и воздушной фазы в разные моменты одного дыхательного цикла (вдоха/выдоха), в том числе поля скоростей Таблица 1. Значения параметров На рисунке 5 представлены поля давления газовой фазы в разные моменты деформирования (с шагом 0.5 с). Длительность дыхательного цикла составляет 4 с. За время t от 0 до 2 с происходит вдох (Рис. 5а–д), в течение двух следующих секунд — выдох (Рис. 5д–и). В конце выдоха легкие и давление воздуха в них возвращаются в исходное состояние: рисунок 5 а соответствует моменту начала, рисунок 5 и — концу дыхательного цикла (t = 0 си t = 4 с). В начальный момент времени t0 (Рис. 5а), в момент перехода от вдоха к выдоху (Рис. 5д) и по завершению выдоха (Рис. 5и) давление в легких равно атмосферному. Элементы сетки, расположенные в непосредственной близости к областям выхода бронхов/входов в легкие (отмечены кружками, см. Рис. 5в), имеют давление более близкое к атмосферному в течение всего дыхательного цикла (Рис. 5а–и). Во время вдоха легкие расширяются, их объем увеличивается, а давление воздуха в них, соответственно, становится ниже. Области легких, прилегающие к диафрагме, подвергаются наибольшему растяжению (преимущественно по вертикальной координате), следовательно, здесь давление имеет наименьшее значение. Воздух из области высокого давления распространяется в область низкого давления и постепенно распространяется по всему объему легких; давление в легких выравнивается. В конце вдоха скорость деформирования замедляется (t = 2 с соответствует максимальному растяжению легких), и воздух распространяется по всему объему, давление воздуха в легких выравнивается с атмосферным (Рис. 5д). Далее следует выдох, объем легких уменьшается (преимущественно за счет движения диафрагмы), давление в легких становится выше и атмосферного, и давления в бронхах, вследствие чего происходит выход воздуха из легких. Наибольший перепад давления (как и во время вдоха) наблюдается в области легких, прилегающих к диафрагме: здесь их объем уменьшается больше всего. По мере замедления скорости изменения объема и выдыхания воздуха через бронхи давление воздуха выравнивается и становится близким к атмосферному (Рис. 5и). К концу выдоха легкие возвращаются в исходное состояние. В процессе решения задачи устанавливаются массовые потоки воздуха на выходах из системы бронхов/входах в легкие (на границах ΓAW/L), которые в дальнейшем используются в качестве граничных условий в подмодели течения воздуха в воздухоносных путях человека (Рис. 6). Всего в рассматриваемой геометрии присутствует 31 вход (14 входов в левом легком и 17 в правом). На рисунке 6а приведены графики изменения массовых потоков воздуха через каждый из входов в легкие в режиме спокойного дыхания. Массовые потоки представляются синусоидами с различной амплитудой. Отличия между потоками воздуха через сечения входов (Рис. 6а) обусловлены разными величинами градиентов давления и площади входов (последняя варьируется от 1.31·10-6до 1.16·10-5м2). Из рисунка 6б, на котором показано изменение суммарного массового потока (в левое и правое легкое и суммарный через 31 вход в легкие) в процессе спокойного дыхания, следует, что массовые потоки воздуха в левом и правом легком примерно одинаковы. Средний суммарный расход воздуха в процессе вдоха (за 2 с) при спокойном дыхании для двух легких составляет 4.43·10-4кг/с, что при плотности воздуха 1.165 кг·м-3 соответствует 0.38 л/с. Следовательно, за 2 с вдоха в легкие человека поступает 0.76 л (0.00076 м3), что соответствует известным физиологическим данным. Был рассмотрен еще один сценарий — учащенное дыхание с периодом t* = 2 с при неизменных остальных параметрах, используемых в граничных условиях задачи (1)–(3). Суммарный массовый поток для учащенного (a) fV R [. (б) t' R I. (в) МММ 1*3 R I. (г) » 1 (д) H R (е) МММ (ж) (з) (и) Рис. 5. Поле давления газовой фазы в легких человека (вид спереди; буквой R обозначено правое легкое, буквой L – левое) в разные моменты времени одного цикла дыхания (вдоха-выдоха) t, [c] : 0 (а); 0.5 (б); 1 (в); 1.5 (г); 2 (д); 2.5 (е); 3 (ж); 3.5 (з); 4 (и) дыхания представлен пунктирной линией на рисунке 6б. При учащенном дыхании средний суммарный расход за время вдоха (за 1 с) составляет 8.82·10-4кг/с, а в легкие поступает или 0.757 л (0.000757 м3) воздуха. Таким образом, предложенная математическая модель может быть использована для описания течения воздуха в легких при различных режимах дыхания. 5. Заключение Предложена модель течения воздуха в дыхательной системе человека, в которой легкие полагаются упруго-деформируемой насыщенной двухфазной пористой средой. Легочное дыхание представляется как совокупность двух связанных процессов: деформирования двухфазного континуума и фильтрации газовой фазы в пористой среде. Сформулированная краевая задача является геометрически нелинейной; ее решение на каждом временном Рис. 6. Массовый поток воздуха: через выходы из бронхов/входы в легкие при спокойном дыхании (а), суммарный массовый поток через входы легких: обоих (сплошная линия), левого (точечная линия), правого (штрихпунктирная линия), а также суммарный массовый поток через входы в обоих легких при учащенном дыхании (пунктирная линия) (б) (a) шаге предлагается отыскивать в виде последовательности решений двух подзадач: подзадачи деформирования пористой двухфазной среды легких и подзадачи относительного движения воздушной фазы в пористой среде. Описан пошаговый алгоритм их решения, для реализации которого авторами разработан комплекс программ. Численное моделирование течения воздуха в легких человека осуществлено для персонализированной геометрии, восстановленной по представленным в открытой базе данных томографическим снимкам. Приводятся картины полей давления газовой фазы в легких человека в различные моменты дыхательного цикла. Дальнейшее изучение процессов дыхания предполагает развитие моделирования в направлении совместного рассмотрения течения воздушной смеси реального состава в воздухоносных путях и деформируемых легких человека, исследования пространственного распространения и оседания частиц в легких человека, возникновения патологических нарушений дыхательной системы, обусловленных негативным воздействием факторов среды обитания. Исследования выполнены при финансовой поддержке Министерства науки и высшего образования Российской Федерации (проект № FSNM-2023-0003).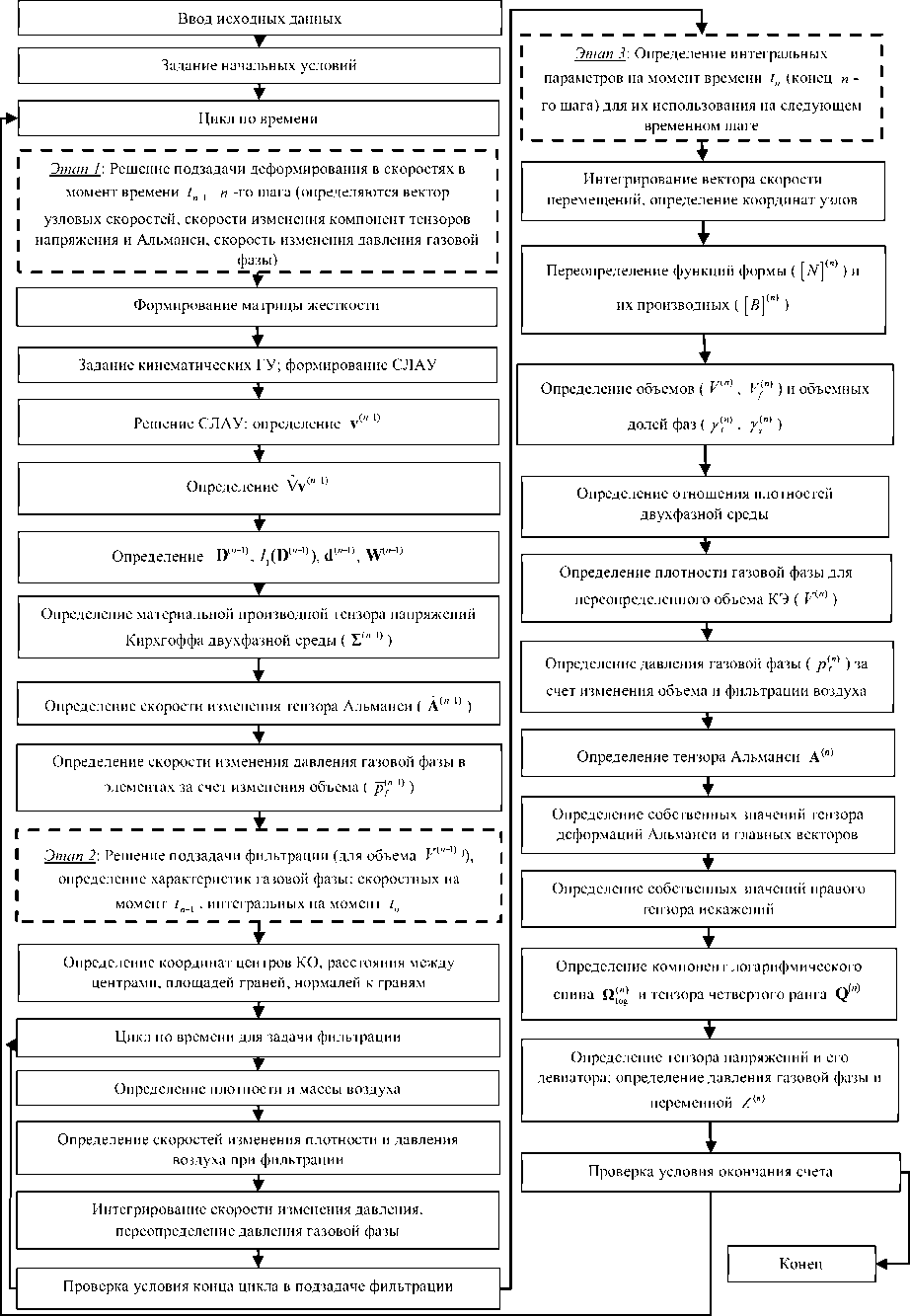
Параметр (размерность)
Значение
Молярная масса воздуха (кг^моль-1)
28.9640-3
Температура газовой фазы (К)
309.75
Универсальная газовая постоянная (м2 кг2 •с-2 К-1 •моль-1)
8.3144
Динамическая вязкость воздуха (Па·с)
18.6^6
Плотность воздуха в легких в начальный момент времени, а также плотность воздуха, поступающего в легкие при температуре 30 °С (кг^м- )
1.165
Проницаемость (м2)
1.5840-9 [11]
Модуль Юнга легочной ткани (Па)
10 000 [38]
Коэффициент Пуассона легочной ткани
0.4 [49]
перемещений, перемещений, деформаций, напряжений, потоков воздуха. В связи с ограничением объема в данной статье приводятся лишь картины полей давления газовой фазы в легких и массовые потоки воздуха через границы ΓAW/L — выходы из системы бронхов (входы в легкие), через которые воздух поступает/выходит во время вдоха/выдоха.

Список литературы Моделирование течения воздуха в упруго-деформируемой пористой среде, аппроксимирующей легкие человека: алгоритм реализации и анализ результатов применения модели
- Ракитский В.Н., Авалиани С.Л., Новиков С.М., Шашина Т.А., Додина Н.С., Кислицин В.А. Анализ риска здоровью при воздействии атмосферных загрязнений как составная часть стратегии уменьшения глобальной эпидемии неинфекционных заболеваний // Анализ риска здоровью. 2019. Т. 4. C. 30–36. DOI: 10.21668/health.risk/2019.4.03
- Grzywa-Celińska A., Krusiński A., Milanowski J. ‘Smoging kills’ – Effects of air pollution on human respiratory system // Annals of Agricultural and Environmental Medicine. 2020. Vol. 27. P. 1–5. DOI: 10.26444/aaem/110477
- Milanowski J. WHO global air quality guidelines: Particulate matter (PM2.5 and PM10), ozone, nitrogen dioxide, sulfur dioxide and carbon monoxide. Geneva: World Health Organization, 2021. URL: https://pubmed.ncbi.nlm.nih.gov/34662007/ (дата обращения: 23.9.2024)
- Гребенев А.Л. Пропедевтика внутренних болезней. М.: Медицина, 2001. 592 с.
- Шкляр Б.С. Диагностика внутренних болезней. Киев: Высшая школа, 1972. 646 с.
- Трусов П.В., Зайцева Н.В., Цинкер М.Ю. Моделирование процесса дыхания человека: концептуальная и математическая постановки // Математическая биология и биоинформатика. 2016. Т. 11, №1. C. 64–80. DOI: 10.17537/2016.11.64
- Rahimi-Gorji M., Pourmehran O., Gorji-Bandpy M., Gorji T.B. CFD simulation of airflow behavior and particle transport and deposition in different breathing conditions through the realistic model of human airways // Journal of Molecular Liquids. 2015. Vol. 209. P. 121–133. DOI: 10.1016/j.molliq.2015.05.031
- RahmanM., ZhaoM., Islam M.S., Dong K., Saha S.C. Numerical study of nano and micro pollutant particle transport and deposition in realistic human lung airways // Powder Technology. 2022. Vol. 402. 117364. DOI: 10.1016/j.powtec.2022.117364
- Анатомия человека. Т. 1 / под ред. М. Сапина. М.: Медицина, 1993. 544 с.
- DeGroot C.T. Numerical Modelling of Transport in Complex Porous Media: Metal Foams to the Human Lung. 2012. URL: https://ir.lib.uwo.ca/etd/655 (дата обращения: 23.9.2024)
- DeGroot C.T., Straatman A.G. A Conjugate Fluid–Porous Approach for Simulating Airflow in Realistic Geometric Representations of the Human Respiratory System // Journal of Biomechanical Engineering. 2016. Vol. 138, no. 3. 4032113. DOI: 10.1115/1.4032113
- Трусов П.В., Зайцева Н.В., Цинкер М.Ю. О моделировании течения воздуха в легких человека: конститутивные соотношения для описания деформирования пористой среды // Вестник Пермского национального исследовательского политехнического университета. Механика. 2020.№4. C. 165–174. DOI: 10.15593/perm.mech/2020.4.14
- Трусов П.В., Зайцева Н.В., Цинкер М.Ю., Нурисламов В.В. Моделирование течения воздуха в упруго-деформируемой пористой среде, аппроксимирующей легкие человека: алгоритм реализации и анализ результатов применения модели // Вычислительная механика сплошных сред. 2024. Т. 17, №2. C. 219–231. DOI: 10.7242/1999-6691/2024.17.2.20
- Лейбензон Л.С. Движение жидкостей и газов в пористой среде. М.-Л.: Гостехиздат, 1947. 244 с.
- Баренблатт Г.И., Ентов В.М., Рыжик В.М. Теория нестационарной фильтрации жидкости и газа. М.: Недра, 1972. 288 с.
- Трусов П.В., Зайцева Н.В., Цинкер М.Ю., Некрасова А.В. Математическая модель течения воздуха с твердыми частицами в носовой полости человека // Математическая биология и биоинформатика. 2021. Т. 16, № 2. C. 349–366. DOI: 10.17537/2021.16.349
- Трусов П.В., Зайцева Н.В., Цинкер М.Ю., Кучуков А.И. Численное исследование нестационарного течения запыленного воздуха и оседания пылевых частиц различных размеров в нижних дыхательных путях человека // Математическая биология и биоинформатика. 2023. Т. 18, №2. C. 347–366. DOI: 10.17537/2023.18.347
- Зенкевич О. Метод конечных элементов в технике. М.: Мир, 1975. 543 с. DOI: 10.18720/SPBPU/2/ek21-22
- Jasak H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows: Thesis submitted for the Degree of Doctor of Philosophy of the University of London and Diploma of Imperial College. London, 1996
- Moraes A., Lage P., Cunha G., da Silva L.F.R. Analysis of the non-orthogonality correction of finite volume discretization on unstructured meshes // Proc. of the 22nd International Congress of Mechanical Engineering. COBEM 2013. Ribeirгo Preto, SP, Brazil, 2013. P. 3519–3530.
- Цинкер М.Ю. Восстановление трехмерной геометрии легких человека на основе данных компьютерной томографии для задач оценки рисков здоровью человека // Фундаментальные и прикладные аспекты анализа риска здоровью населения: Материалы Всероссийской научно-практической интернет-конференции молодых ученых и специалистов Роспотребнадзора с международным участием. Пермь, 2021. C. 372–375.
- VIA/I-ELCAP Public Access Research Database. URL: http://www.via.cornell.edu/databases/lungdb.html (дата обращения: 23.9.2024)
- Yushkevich P.A., Piven J., Hazlett H.C., Smith R.G., Ho S., Gee J.C., Gerig G. User-guided 3D active contour segmentation of anatomical structures: Significantly improved efficiency and reliability // NeuroImage. 2006. Vol. 31. P. 1116–1128. DOI: 10.1016/j.neuroimage.2006.01.015
- Клаучек С.В., Лифанова Е.В. Физиология дыхания. Волгоград: Волгоградский Государственный Медицинский Университет, 2005. 88 с.
- Михайлова Н.Л., Генинг Т.П., Долгова Д.Р. Физиология дыхания. Ульяновск, 2015. 69 с.
- Werner R., Ehrhardt J., Schmidt R., Handels H. Patient-specific finite element modeling of respiratory lung motion using 4D CT image data // Medical Physics. 2009. Vol. 36, no. 5. P. 1500–1511. DOI: 10.1118/1.3101820
- Ehrhardt J., Werner R., Schmidt-Richberg A., Handels H. Statistical Modeling of 4D Respiratory Lung Motion Using Diffeomorphic Image Registration // IEEE transactions on medical imaging. 2011. Vol. 30, no. 2. DOI: 10.1109/TMI.2010.207629
- Werner R. Biophysical Modeling of Respiratory Organ Motion // 4D Modeling and Estimation of Respiratory Motion for Radiation Therapy / ed. by J. Ehrhardt, C. Lorenz. Springer Berlin, Heidelberg, 2013. P. 61–84. DOI: 10.1007/978-3-642-36441-9_4
- Chen D., Xie H., Gu L., Liu J., Tian L. Generation of a local lung respiratory motion model using a weighted sparse algorithm and motion prior-based registration // Computers in Biology and Medicine. 2020. Vol. 123. 103913. DOI: 10.1016/j.compbiomed.2020.103913
- Романьков Л.В. Тезисы лекций по пропедевтике внутренних болезней. Гомель: УО Гомельский государственный медицинский университет, 2008. 172 с.
- Маев И.В., Шестаков В.А., Ляхова Т.М., Бусарова Г.А., Пономаренко В.Б., Гончаренко А.Ю., Лебедева Е.Г. Пропедевтика внутренних болезней. Т. 1. М.: Академия, 2012. 352 с.
- Kushwaha N., Kalpesh S., Parmar L.D. A study of chest expansion measurement in healthy adults with two different instructions // International Journal of Scientific Research. 2018. Vol. 7, no. 8. P. 42–44.
- Паспорт. Самоконтроль уровня здоровья (физическое состояние, психологическое состояние, отношение к своему здоровью). Саратов, 0048. URL: https://www.nsmu.ru/socium/student_government/%D0%9F%D1%80%D0%B8%D0%BB%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5%2016.pdf
- Уэст Д. Физиология дыхания. Основы. М.: Мир, 1988. 196 с.
- Линденбратен Л.Д. Лучевая диагностика поражений диафрагмы (краткий очерк) // Радиология - практика. 2001.№2. C. 6–21.
- Kolбř P., Neuwirth J., Šanda J., Suchбnek V., Svatб Z., Volejnнk J., Pivec M. Analysis of diaphragm movement, during tidal breathing and during its activation while breath holding, using MRI synchronized with spirometry // Physiological Research. 2009. P. 383–392. DOI: 10.33549/physiolres.931376
- Базылев В.В., Парамонова Т.И., Вдовкин А.В. Анализ положения и подвижности диафрагмы у взрослых с нормальной функцией легких до и после кардиохирургических операций // Лучевая диагностика и терапия. 2017.№1. C. 53–63. DOI: 10.22328/2079-5343-2017-1-53-63
- Nakao M., Nakao M., Kokubo M., Kokubo M. Simulating lung tumor motion for dynamic tumor-tracking irradiation // IEEE Nuclear Science Symposium Conference Record. 2007. P. 4549–4551. DOI: 10.1109/NSSMIC.2007.4437123
- Werner R., Ehrhardt J., Schmidt R., Handels H. Modeling respiratory lung motion: a biophysical approach using finite element methods // Medical Imaging 2008: Physiology, Function, and Structure from Medical Images. 2008. DOI: 10.1117/12.769155
- Trusov P.V., Zaitseva N.V., Tsinker M.Y. A mathematical model of the human respiratory system considering environmental influence // AIP Conference Proceedings: 28th Russian Conference on Mathematical Modelling in Natural Sciences. Perm: AIP Publishing, 2020. 060007. DOI: 10.1063/5.0003562
- Xiao H., Bruhns O.T., Meyers A. Logarithmic strain, logarithmic spin and logarithmic rate // Acta Mechanica. 1997. Vol. 124. P. 89–105. DOI: 10.1007/bf01213020
- Xiao H., Bruhns O.T., Meyers A. Hypo-elasticity model based upon the logarithmic stress rate // Journal of Elasticity. 1997. Vol. 47. P. 51–68. DOI: 10.1023/A:1007356925912
- Поздеев А.А., Трусов П.В., Няшин Ю.И. Большие упругопластические деформации: теория, алгоритмы, приложения. М.: Наука, 1986. 232 с.
- Weibel E.R. Morphometry of the Human Lung. New York: Springer Verlag, Academic Press, 1963. URL: http://dx.doi.org/10.1007/978-3-642-87553-3
- Gehr P., Bachofen M., Weibel E.R. The normal human lung: ultrastructure and morphometric estimation of diffusion capacity // Respiration Physiology. 1978. Vol. 32. P. 121–140. DOI: 10.1016/0034-5687(78)90104-4
- Armstrong J.D., Gluck E.H., Crapo R.O., Jones H.A., Hughes J.M. Lung tissue volume estimated by simultaneous radiographic and helium dilution methods. // Thorax. 1982. Vol. 37. P. 676–679. DOI: 10.1136/thx.37.9.676
- Kamschulte M., Schneider C.R., Litzbauer H.D., Tscholl D., Schneider C., Zeiner C., Krombach G.A., Ritman E.L., Bohle R.M., Langheinrich A.C. Quantitative 3D Micro-CT Imaging of Human Lung Tissue // Fortschr Rцntgenstr. 2013. Vol. 185. P. 869–876. DOI: 10.1055/s-0033-1350105
- Denison D.M., Morgan M.D., Millar A.B. Estimation of regional gas and tissue volumes of the lung in supine man using computed tomography // Thorax. 1986. Vol. 41, no. 8. P. 620–628. DOI: 10.1136/thx.41.8.620
- Lai-Fook S.J., Hyatt R.E. Effects of age on elastic moduli of human lungs // Journal of Applied Physiology. 2000. Vol. 89, no. 1. P. 163–168. DOI: 10.1152/jappl.2000.89.1.163
- Unleash the Power of ParaView. URL: https://www.paraview.org/ (дата обращения: 23.9.2024)


