Моделирование троированного мажоритарного элемента в quartus prime state machine

Система проектирования программируемых логических интегральных схем (FPGA) Intel Quartus Prime [1] имеет опцию State Machine для автоматического синтеза схемы в соответствии с графом конечного автомата через промежуточный этап получения программы на языке VHDL.

Представляет интерес исследование возможности синтеза троированного мажоритарного элемента [2, 3].

Для этих целей используется автоматический синтез конечного автомата по графу переходов.

1.    Автоматический синтез

Попробуем автоматически синтезировать двоичный сумматор [3, 4] (табл. 1).

Таблица 1. Таблица истинности сумматора

a	b	c	pl ( abc )	p2 ( abc )	p3 (abc )
0	0	0	0	0	0
0	0	1	0	0	0
0	1	0	0	0	0
0	1	1	1	1	1
1	0	0	0	0	0
1	0	1	1	1	1
1	1	0	1	1	1
1	1	1	1	1	1

Логические функции, соответствующие табл. 1, имеют вид:

b pl(abc) — ab V ас V be p2 (abc) — ab V ас V be p3 (abc} — abv acV be

Попробуем выполнить автоматический синтез схемы соответствующего комбинационного автомата – полного сумматора по высокоуровневому описанию в виде графа автомата [3, 4]. Запускаем опцию State Machine и создаем граф из одной вершины (рис. 1).

Рис. 1. Задание графа из одной вершины в State Machine

Таблицу переходов из состояния 1 в состояние 1 в State Machine задаем с использованием символов следующих логических операций:

| – "ИЛИ";

& – "И";

~ – "НЕ".

Настройка выполняется в окне

Transition Properties (рис. 2).

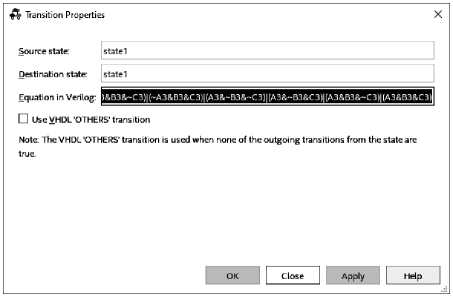
Рис. 2. Таблица переходов комбинационного автомата

Тогда итоговый граф будет выглядеть следующим образом (рис. 3):

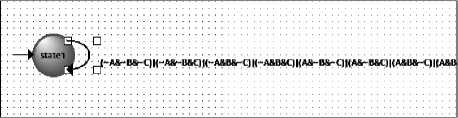
Рис. 3. Граф комбинационного автомата с логической функцией переходов из состояния 1 в состояние 1

Таблицу истинности в State Machine задаем во вкладке Actions окна State Properties (рис. 4).

А State Properties

Рис. 4. Задание таблицы истинности

Входные наборы приходится повторять два раза – по числу используемых функций.

• 2.    Компиляция комбинационного автомата, заданного в виде State Machine File

Необходимо сначала получить VHDL-файл (рис. 5).

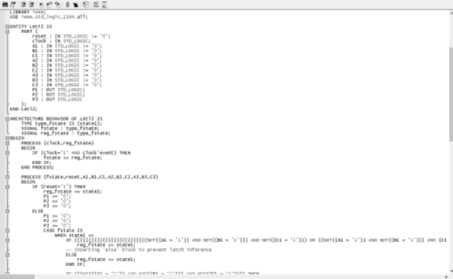
Рис. 5. Фрагмент VHDL-файла, созданного по графу в State Machine

Проводим компиляцию VHDL-файла (рис. 6).

Рис. 6. Результаты компиляции VHDL-файла, созданного по графу в State Machine

Просмотр результатов осуществляется с помощью средства Map Viewer (рис. 7).

На рис. 7 показаны логические элементы (ячейки) LOGIC CELL COMB. Каждая логическая ячейка содержит постоянное запоминающее устройство ПЗУ, называемое производителями LUT (Look Up Table), вероятно, потому, что туда загружается таблица истинности требуемой логической функции [5]. При выделении соответствующей ячейки отображается логическая функция (рис. 8–10).

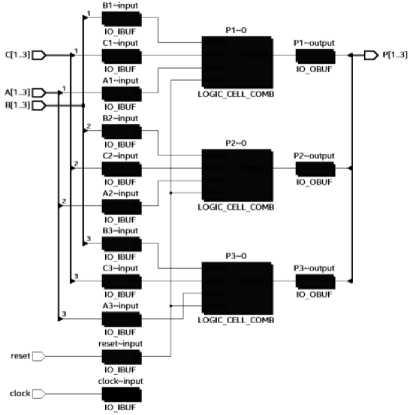
Рис. 7. Map Viewer схемы автомата, созданной по графу State Machine

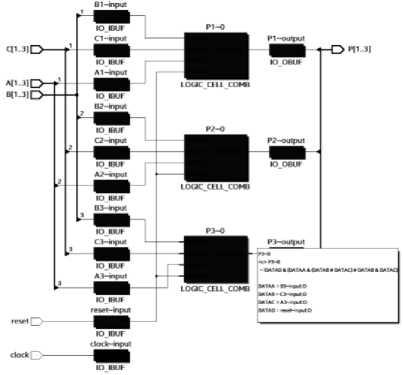
Рис. 10. Map Viewer с отображением логической функции p3

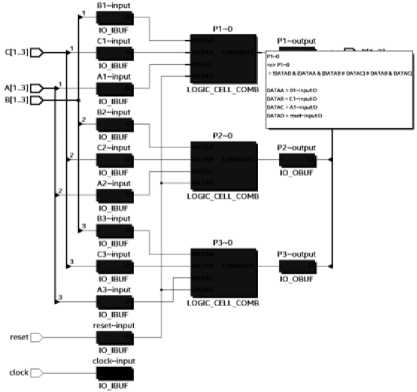
Рис. 8. Map Viewer с отображением логической функции p1

Необходимо отметить имеющееся различие символов операций с теми, что были использованы при настройке графа в State Machine. Так, инверсия на рис. 8–10 обозначена восклицательным знаком, дизъюнкция – решеткой. Очевидно, что $ на рис. 8 – это сумма по модулю два (Исключающее ИЛИ).

Шестнадцатеричные коды настройки логических элементов (ячеек) LOGIC CELL COMB показаны на рис. 11.

• 3.    Расшифровка шестнадцатеричных кодов логических функций комбинационной схемы, автоматически синтезированной в State Machine File

Расшифруем логическую функцию и для настройки 00Е8 получаем (рис. 11).

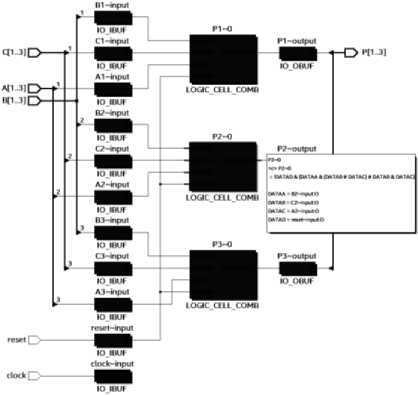
Рис. 9. Map Viewer с отображением логической функции p2

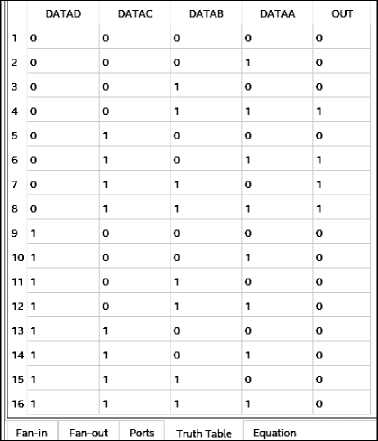
Рис. 11. Таблица истинности функции p1, настройка 00Е8

Таким образом, действительно задана мажоритарная логическая функция – функция переноса:

p 1( abc )= ab ∨ ac ∨ bc.

Действительно, функция соответствует табл. 1 с учетом нулевого сигнала сброса.

Временные диаграммы окна Waveform Editor с заданными значениями входных сигналов показаны на рис. 12.

Рис. 12. Окно Waveform Editor с заданными значениями входных сигналов

Выводы

Таким образом, использование графа автомата с одним состоянием позволяет провести автоматический синтез схемы комбинационного автомата по таблице истинности, задаваемой в виде формул соответствующих конъюнкций. Причем ее необходимо повторять столько раз, сколько имеется выходных функций.

Символы логических операций, используемые при задании графа, имеют существенные отличия от символов, отображаемых средством Map Viewer по результатам синтеза.

В дальнейшем целесообразно установить имеющиеся ограничения на количество входных переменных и выходных функций при подобном задании комбинационного автомата, а также попытаться найти возможности задания таблиц истинности в более удобном – числовом – виде, возможно, и с использованием языков описания аппаратных средств типа VHDL.