Моделирование турбулентной естественной конвекции на основе 2-жидкостного подхода

Теплообмен в турбулентных естественно-конвективных потоках представляет большой интерес как в теоретическом, так и в прикладном аспекте. В качестве примера достаточно привести природные явления, где турбулентная конвекция играет решающую роль [1] . Процессы конвекции значимы также и в промышленности. Например, естественная конвекционная теплопередача служит надежным и экономичным методом охлаждения в быстрорастущей электронной промышленности, где сотни модулей могут размещаться на небольшом основании. Поскольку плотность этих тепловыделяющих элементов постоянно увеличивается, испускаемое тепло должно эффективно отводиться не только для их защиты, но и для увеличения срока службы. Часто возникает необходимость охлаждения внутренних поверхностей вертикальных открытых воздуховодов за счет естественной конвекции, где скорости теплопередачи низкие. Таким образом, владение информацией о поведении естественного конвекционного потока в замкнутых пространствах не только полезно, но и необходимо, особенно в системах теплоносителей, используемых в различных областях ядерной и солнечной энергетики [2] .

Вследствие важности проблема естественной конвекции в последние годы привлекает все большее внимание исследователей [3] . Существующие конвективные процессы можно разделить на свободные и вынужденные. Такой градации придерживаются авторы большинства публикаций [4, 5] . Изучением вопросов свободной и вынужденной конвекции занимались многие ученые, в частности, описание конвективных систем подробно приводится в [6 –8] . Естественная конвекция бывает как ламинарной, так и турбулентной. В природных условиях, а также в больших помещениях конвекция имеет турбулентный характер. Поэтому моделирование турбулентности — одна из проблем при изучении процессов конвекции. В последнее время наравне с лабораторными испытаниями используется численный эксперимент — исследование явления при помощи методов вычислительной гидродинамики (Computational Fluid Dynamics, CFD). Современные программные комплексы позволяют проводить исследования большого числа гидродинамических, тепло- и массообменных процессов [9 –12] . Наиболее распространены комплексы ANSYS, COMSOL Multyphysics, FlowVision и другие, которые содержат различные модели турбулентности и предназначены для исследования большинства потоков, встречающихся в природе и

Статья опубликована в открытом доступе по лицензии CC BY 4.0

в создаваемых человеком технологиях, имеющих турбулентный характер. Поэтому применение пакетов программ для решения той или иной задачи гидродинамики ставит ученых перед необходимостью выбора подходящей модели турбулентности. В основном существует три подхода к математическому моделированию турбулентности. Первый подход основан на прямом численном моделировании (Direct Numerical Simulation, DNS), базирующемся на гипотезе о достаточности уравнений Навье–Стокса для описания турбулентных течений. При этом численно решается нестационарная система уравнений Навье–Стокса в трехмерной постановке. Причем для интегрирования требуются расчетные ячейки, размеры которых меньше, чем Колмогоровский масштаб. DNS-подход требует большого объема вычислительных ресурсов, и его использование для расчета сложных гидродинамических задач в настоящее время не представляется возможным. Во втором подходе производится осреднение уравнений Навье–Стокса по числу Рейнольдса (Reynolds Averaged Navier–Stokes, RANS), которое приводит к незамкнутой системе уравнений. Поэтому для замыкания этой системы дополнительно вводятся модели турбулентности. Все они называются RANS-моделями. Достоинством RANS-моделей является то, что для их численной реализации требуются существенно меньшие вычислительные ресурсы по сравнению с методами DNS [13] . По этой причине подход RANS находит наиболее широкое приложение при решении инженерных задач. Несмотря на значительный прогресс, достигнутый в области моделирования турбулентных течений на основе RANS-моделей, все еще остаются нерешенные проблемы, связанные с расчетом динамики и теплообмена в турбулентных естественноконвективных потоках. Как показано в ряде исследований [14, 15] , применение наиболее распространенных при решении прикладных задач конвективного теплообмена двухпараметрических полуэмпирических моделей турбулентности типа k - ε не обеспечивает необходимой для практики точности описания естественноконвективных турбулентных течений. В связи с этим на протяжении многих лет предпринимаются попытки усовершенствования существующих и построения новых моделей турбулентности для течений данного класса. Во многих работах основной акцент делается на необходимости прямого учета влияния эффектов плавучести в традиционных моделях турбулентности (например, в k - ε -моделях) путем включения дополнительных членов в соответствующие уравнения переноса турбулентных характеристик потока [16, 17] . Однако такой метод приводит как к введению и определению ряда дополнительных эмпирических констант, так и к увеличению числа дифференциальных уравнений, входящих в модель. Это в свою очередь дополнительно усложняет и без того трудоемкие с вычислительной точки зрения низко рейнольдсовые версии k - ε -моделей и других, аналогичных им.

Еще одним направлением в моделировании естественной конвекции является использование более сложных RANS-моделей, в частности, моделей переноса рейнольдсовых напряжений (RSM). Однако, из-за сложности, их приложение ограничивается главным образом решением достаточно простых модельных задач. Проведение же широких численных исследований и параметрических расчетов, необходимых для решения практических задач конвективного теплообмена, не всегда оправдано и эффективно. В последние годы широкую популярность получили модели, существенно превосходящие традиционные как с точки зрения вычислительной эффективности, так и с точки зрения точности решений охватываемого круга задач вынужденной конвекции. В частности, к их числу можно отнести однопараметрическую модель, основанную на решении уравнения переноса турбулентной вязкости, — модель Спаларта–Аллмараса (SA) [18] , и двухпараметрическую модель Ментера (SSG) [19] , представляющую собой комбинацию стандартной k - ε -модели и известной k - ω -модели Уилкокса [20] . Возможности этих моделей и их существенное превосходство над стандартными k - ε -моделями применительно к решению ряда сложных задач вынужденной конвекции продемонстрированы во многих работах. Так, в [21] эти модели использованы для решения некоторых задач естественной конвекции и отмечено, что они дают более точные решения, чем сложные модели. Однако, по мнению авторов настоящей работы, существенным недостатком практически всех RANS-моделей является то, что при решении задач естественной конвекции они не в состоянии представлять переход от ламинарного потока к турбулентному. Например, в упомянутой работе для расчета турбулентной конвекции около нагретой вертикальной пластины во всех рассмотренных моделях зона перехода течения от ламинарного режима к турбулентному задавалась на основе опытных исследований. К третьему подходу математического моделирования турбулентности можно отнести так называемый 2-жидкостный подход, предложенный Сполдингом [22, 23] . С его помощью исследовались: неустойчивость Релея–Тейлора [24] ; процесс горения [25] ; турбулентные стратифицированные течения [26] ; ограниченное и свободное турбулентные сдвиговые течения [27] и другое. Дальнейшее развитие 2-жидкостный подход получил в работах [28, 29] , где представлена его способность с большой точностью описывать турбулентные процессы переноса импульса и тепла в анизотропных турбулентных течениях. Целью настоящей работы является демонстрация возможности 2-жидкостного подхода к учету естественной турбулентной конвекции воздуха около нагретой вертикальной пластины. Несмотря на свою относительную простоту, выбранная задача содержит в себе все главные элементы, характерные для течений вблизи стенки, обусловленных силами плавучести. Наряду с надежными экспериментальными данными [30,

31] для рассматриваемого течения также представлены результаты расчетов по моделям SA иRSM из [21] .

• 2.    Система уравнений турбулентной естественной конвекции около нагретой вертикальной бесконечной пластины в 2-жидкостном подходе

В работе [28] показано, что турбулентный поток можно представить в виде гетерогенной смеси двух жидкостей не только с разными скоростями, но и с разными температурами:

V l i = V i +4, V 2 i = V i - ^ i , T 1 = T + 1, T 2 = T - 1.                        (1)

В выражениях (1) обозначено: V _i , T — осредненные скорость и температура турбулентного потока; ϑ i , t — относительные скорость и температура гетерогенной смеси. Вывод уравнений турбулентной термодинамики подробно приведен в упомянутой работе. Исходя из этих уравнений, приведем систему уравнений для конвективного течения воздуха со скоростью V 0 около нагретой до температуры T w вертикальной пластины длиной L (Рис. 1) :

^dP^U , ^dP^V ∂x ∂y ^,

• u^ + v^t = I ("IT - u^ + gT-T ,

∂x ∂y ∂y ∂y          T 0

• U^ + v|u = -(1 - C s wf + 4 (pv xy % \ - K f u + g*

∂x ∂y           ∂y ρ∂y ∂y         T 0

Utt +v|r— -C s utt + (p^ |^v

∂x ∂y       ∂y ρ∂y ∂y идг+vdr=~tt (ркдг

∂x ∂y ρ∂y ∂y

- K f ϑ - ϑ ² T _T ^t ₀2 ^∂_∂^T_y ,

-

U^+vdr = - дг^+^ГкУу dt - Ktt, ∂x ∂y ∂y ρ∂y ∂y vxy — 3 v+2

uϑ

9U/ду

V yy — 3v + 2

ϑϑ dU/ду

k y — 3k +2

tϑ dT/ду

pT — P o T o .

Здесь: x — координата, направленная вдоль вертикальной пластины; y — координата, перпендикулярная к пластине; U,V — продольная и поперечная скорости; u,ϑ — продольная и поперечная относительные скорости; T — температура воздуха; T 0 — температура воздуха вдали от пластины; ρ — плотность воздуха; ρ 0 — плотность среды вдали от пластины; ν — кинематическая вязкость; k — коэффициент температуропроводности воздуха; ν xy , ν yy — молярные вязкости; k y — молярный коэффициент температуропроводности; g — ускорение

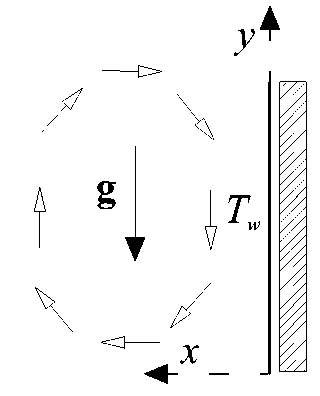
Рис. 1. Схема к задаче

свободного падения; Cs — поправочный коэффициент; Kf и Kt — коэффициенты трения и теплообмена; t — нефлуктуирующая температура. Давление везде имеет постоянное значение. Ввиду малости пренебрегаем продольными производными в диффузионных членах правых частей уравнений (2). Как видно, в четвертом уравнении в правую часть введена дополнительная термическая сила fT=-P$T t^Tr- (3)

• ^T T ₀ ² ∂y

В (3) параметр ϑ _T имеет размерность скорости, и путем численного исследования выявлено, что он равен $ _T = 2.05 м/с. Во многих турбулентных течениях характерная скорость V 0 такова, что $ _T /V 0 < 1 . Поэтому в задачах с вынужденной конвекцией сила f T может быть существенно меньше, чем другие силы, следовательно, эту силу можно не учитывать. Однако в естественных конвекциях скорость потока невелика и в этих случаях пренебрегать термической силой нельзя. Ниже будет показано, что в естественном конвективном течении около нагретой вертикальной пластины переход ламинарного потока в турбулентный происходит благодаря именно этой силе, потому что в переходной зоне скорость потока мала.

Систему уравнений (2) приведем к б езразмерному виду. Для этого все скорости отнесем к величине c размерностью скорости у/gL(T w — T 0 )/T 0 , все расстояния — к длине L = 1 м, все температуры — к температуре окружающей среды T 0 = 289 К, а плотность воздуха — к плотности окружающей среды р ₀ = 1.23 кг/м ³ . Температура нагретой пластины составляет T 0 = 333 К. Для численной реализации системы (2) удобно ввести переменные Мизеса ξ и ψ [32, 33] :

ψ∂ψ ψ∂ψ

• £ = x, pU = ——, pV = ——. ∂y ∂x

  В новых переменных первое уравнение в (2) — уравнение неразрывности, удовлетворяется автоматически. Численное решение системы (2) проведем на основе неявной конечно-разностной схемы. В поперечном направлении воспользуемся центральными разностями. Для решения неявной схемы применим метод прогонки. Шаги интегрирования по переменным Мизеса возьмем равными А£ = 0.00002 и Аф = 0.001 , а число расчетных точек в поперечном направлении пусть составляет 1000. Заметим, что вычислительные эксперименты позволили сделать вывод о несущественном влиянии параметров сетки на результат. Для замыкания системы разрешающих уравнений (2) поставим на пластине условия прилипания, а вдали от нее все скорости приравняем нулю. На входе, то есть при £ = 0 , безразмерные относительные скорости зададим следующими: u= 10 ^-20 , $ = 0 . Для более точного расчета вязкости воздуха используем закон Сазерленда:

v v0

T \ ^2.5 T 0 + 110.4

T 0 J   T +110.4 .

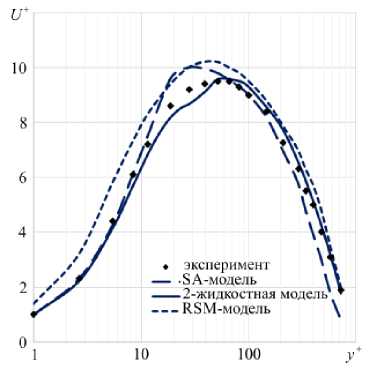
Рис. 2. Профиль безразмерной продольной скорости

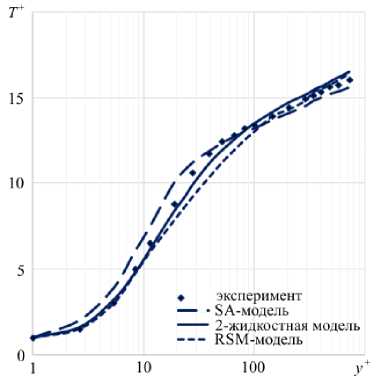
Рис. 3. Профиль безразмерной избыточной температуры

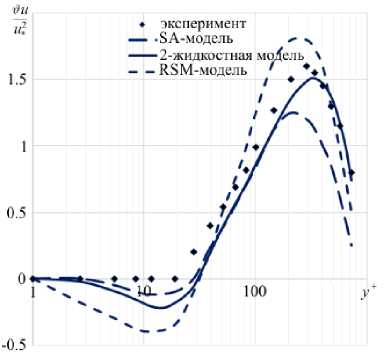
Рис. 4. Профиль турбулентных напряжений

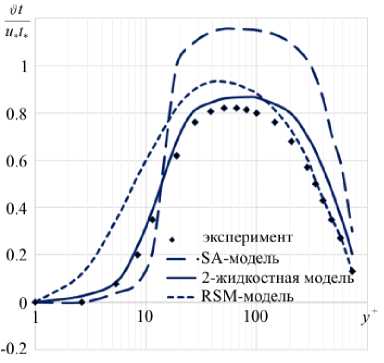
Рис. 5. Профиль турбулентного потока температуры

Нуссельта Nu x в зависимости от числа Релея Ra , которые связаны с параметрами модели соотношениями.

Nu x =

x ∂T

T w -T 0 ∂y

w

Ra = PrRe W x ³ ,

где числа Прандтля и Рейнольдса взяты из работы [21] . Из рисунка видно, что, примерно начиная со значения Ra =10 9 , наступает турбулентный режим, и число Нуссельта начинает резко увеличиваться по сравнению со значением, характерным для ламинарного режима. Результаты 2-жидкостной модели хорошо описывают все режимы течения, включая и переходный от ламинарного к турбулентному.

Необходимо отметить, что при моделировании естественной конвекции большую роль играет турбулентная термическая сила. Расчеты по определению числа Нуссельта показали, что без учета данной силы не возможен переход от ламинарного к турбулентному режиму течения, то есть поток остается ламинарным и на больших расстояниях от пластины. Переход в турбулентный режим не наблюдается даже при сильном увеличении начальных возмущений, например при и = 0.1 , v = 0 . Данное обстоятельство свидетельствует о необходимости учета турбулентной термической силы в расчетах турбулентной естественной конвекции, несмотря на ее малость по сравнению с другими силами.

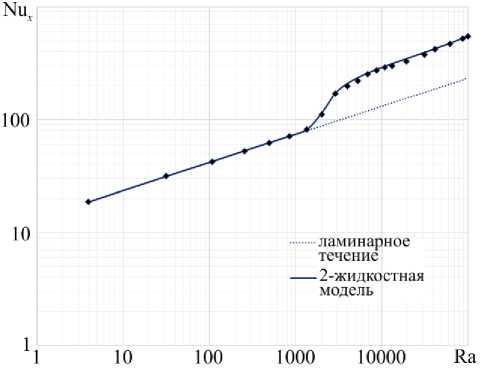
Рис. 6. Зависимость числа Нуссельта от числа Релея согласно 2-жидкостной модели турбулентности

• 4.    Заключение

Полученные численные результаты показывают, что 2-жидкостная модель позволяет более точно описать естественную конвекцию, по сравнению с хорошо известными RANS-моделями. Доказано, что при моделировании естественной конвекции необходимо учитывать термическую силу, которая инициирует переход от ламинарного режима к турбулентному без учета дополнительных поправок. 2-жидкостная модель проста для численной реализации и имеет хорошую устойчивость, поэтому ее можно рекомендовать для исследования течений естественной конвекции.