Моделирование водоохранных мероприятий в бассейне реки

Речные бассейны – характерные объекты интенсивной антропогенной нагрузки. Одно из направлений снижения этой нагрузки состоит в регламентации хозяйственной деятельности посредством установления определенных норм и требований к количеству и качеству сточных вод от предприятий. Достаточно полное представление об этом дают монографии [1, 2].

Другое направление – регулярные природоохранные мероприятия по экологическому мониторингу и очистке скапливающихся загрязнений в водной среде и донных отложениях, бытового мусора, паразитической биоты и т.п. Такие мероприятия требуют больших затрат, поэтому актуальна задача их минимизации с использованием естественной самоочи-щающей способности природной среды.

Цель данной статьи – рассмотреть схематически эту задачу, которая не укладывается в традиционные постановки задач оптимального управления. Для этого строится двухуровневая модель дискретно-непрерывной системы (ДНС), на нижнем уровне которой описываются непрерывные распределения примесей вдоль русел рек, а на верхнем - фигурирует сеть операторов, отражающая структуру бассейна как системы рек. Понятие абстрактной сети операторов введено впервые в [3] вместе с общими достаточными условиями как обобщением таковых для дискретной динамической модели [4].

Использование двухуровневой модели дает возможность эффективно декомпозировать соответствующую задачу управления на «однородные» подзадачи так, чтобы применить известные методы для однородных непрерывных и дискретных систем, в данном случае методы, развитые в работах В.Ф. Кротова и его последователей [5-8].

• 1.    Постановка задачи

Задача рассматривается в упрощенной постановке на примере условного речного бассейна: главная река с двумя притоками (рис. 1).

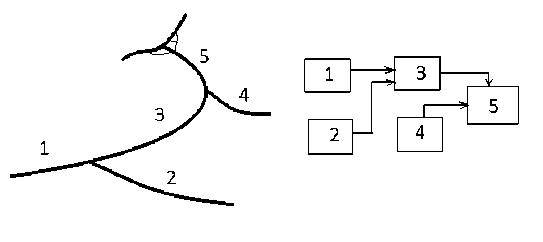
Рис. 1

Можно построить камерную модель этого бассейна, разделив его на 5 камер, как показано на рис. 1. В каждой камере распределение концентрации загрязнений вдоль русла описывается некоторой дифференциальной системой, которую примем линейной dp = A(t) Р + B(t) r + 5(t), t G [0, tF ], 0 < r < rmax,        (1)

dt где t имеет смысл расстояния от начала соответствующей камеры, Р -вектора концентраций загрязнений, r - вектора интенсивностей природоохранных мероприятий, 5 - вектора потоков поступающих загрязнений. Здесь все величины имеют номер соответствующей камеры k = 1, ^, 5: tk, pk, ..., который для краткости опущен. Задача состоит в обеспечении допустимых концентраций в устьях рек, pk (tF) < pkmax, с минимумом суммарных затрат, определяемых величиной

• 5                      t kF

Q = 2 q kF , q kF = J c k ⁽ t ) r k ⁽ t ) dt .

k = 1                   0

Размерности векторов концентраций в разных камерах могут быть разными в зависимости от формы и размеров поперечного сечения русла, условий перемешивания и т.п.

Примем для простоты p и r одномерными, B = - 1, A , c , s - постоянными для каждой камеры. При естественном предположении p >  0 для любых управлений в указанных границах ограничение p ( t_F ) <  p _max можно заменить штрафом и минимизировать взвешенную сумму

I = У I , I = ( в q„ + (1 - в ) p , J, 0 < в <  1. k k       k kF           k kF           k

Для решения задачи построим соответствующую двухуровневую дискретно-непрерывную модель, на верхнем уровне которой фигурирует сеть операторов, которая, согласно [3], определяется следующим образом.

Пусть имеется N операторов произвольной природы f : X. х U ^ Y (у = f (к, х,»)).                   (2)

k k k     k     k         kk nk

Вводятся подмножества X kq , такие, что П X kq = X k . Будем говорить, q = 1

что выход оператора l подается на вход оператора к , если для некоторого q имеет место равенство / ( к , q , x_k ) = y l , где / ( к , q , x_k ) - оператор проектирования на подмножество X kq .

Пусть рассматриваемые операторы соединены указанным образом по некоторой схеме, представляемой ориентированным графом (рис. 2). Предполагается, что для данного к между номерами q и l имеет место взаимно-однозначное соответствие. Иными словами, X _к олицетворяет множество входов к -го оператора, занятых в соединениях, а U _к - множество свободных входов.

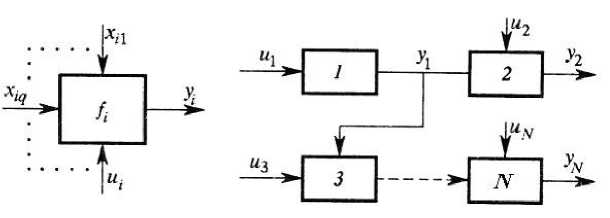
Рис. 2

В качестве общей модели двухуровневой управляемой системы предлагается следующая конкретизация указанной абстрактной модели. Представим условие (хк, ик) е В(к) в форме хк е Х(к), ик е U(к, хк), где Х(к) -проекция на Xк, U(к, хк) - сечение В(к) при данных к , хк. Пусть на некотором подмножестве K' с K = {1,.„,N} имеем u = (ud,mc), где ud -произвольной природы, а mc - некоторый непрерывный управляемый процесс, так что сечение множества U(k, x) при фиксированных x, ud есть допустимое множество Dc (k,x,ud) с соответствующей дифференциальной системой

c xc = Т = fc (z, t, x , u), te T(z), dt xc e Xc (z,t) с Rn(k), uc e Uc (z,t,xc) с Rp(k), z = (k,x,ud).

Оператор правой части (2) сводится к следующему:

Ук = f ^{( k} , ^x , ^u ) = ^{6 ( z} , ^Y ),

Y = ( t, , x c ,t_F , x F ) e { Y : t, = t ( z ), x c = ^ ( z ), t_F = S ( z ), x F еГ ^c ( z )}.

Решением этой комбинированной системы будем считать набор m = (x(k), u(k)) e D, где при k e K':

u ( k ) = ( ud ( k ), m^c ( k )), m^c e D ^c ( t , x ( k ), ud ( k )).

Задача оптимизации формулируется для верхнего уровня как задача о минимуме функционала

NNN

I = E I k ⁽ Ук ) = E I k ⁽ f ^{( k} , ^x k , ^u k )) = E f ^{0 ( k} , ^x k , ^u k ) 1                                          1                                                                           1

на множестве D наборов m = {(xk,uk)}, k = 1,.„,N, связанных указанны- ми соотношениями сети и возможными дополнительными ограничениями вида (xk, uk) e B(k), где B(k) - заданное при каждом k множество. Тре буется найти минимизирующую последовательность {ms} с D, т.е. такую, что I (ms) ^ inf I.

Для решения этой общей задачи вводится множество E элементов m , не связанных сетевыми условиями - равенствами х (k , j , x_k ) = y_: - на верхнем уровне и дифференциальными связями на нижнем.

Достаточные условия оптимальности для нее получаются по аналогии с динамическими дискретно-непрерывными процессами [9, 10].

Для номеров k e K' вводится дополнительно параметрическое семейство (с параметром z) гладких функций Y :Rm(k)+1 ^ R. Строится соот- ветствующая модификация обобщенного лагранжиана [9, 10]:

L=

E k \ K ‘ R k E R k , K ′

где

N

Rk = R (k, x, u) = E (Y( k, I, f (k, x, u)) - y( I, k, x( k, I, x))) - f0 (k, x, u), i=1

где y ( k , I , y_k ), k , I = 1, ^ , N - произвольные функционалы, такие, что

Y(k, I, yk) ^ 0, если равенство x(k, j, xk) = yz отсутствует (отсутствует связь l ^ к).

R k = G ( z , Y ) + j ( R c ( z , t , x c ( z , t ), u^c ( z , t )) - ^ ( z ) dt ,

T ( z )

N

G ( ^z , f ) = E H k , l , Ук ) ^- y ( l , ^k , x ( ^k , j , x k ) ) ) + l = 1

+ Y ( z , t i , x c ) - Y ( z , t F , x F ) + j u ( z , t ) dt - I k ( 0 ( z , Y ) ) , ^T ( z )

(\         T /                  \          I            \ c c         c1 cc            c c         c            c z, t, x , u ) = Yx f ( z, t, x , u ) + Фt (z, t, x ),

Y ( z , t ) = sup { R^c : x^c e X ^c ( z , t ), u e U ^c ( z , t , x^c ) }, где y_k = 0 ( z , Y ) при к e K ', y_k = f ( к , x , u ) при к e K \ K' . Обозначим Y ( k ) = sup { G ( z , Y ) : Y еГ ^с ( z ) , x c e X ^c ( z , t i ), x F e X ^c ( z , t_F ), u^d e U ^d ( к ), x e X ( k )}.

Легко убедиться, что L ( m ) = I ( m ) при m e D , т.е. при выполнении отброшенных связей. Для этого рассмотрим вначале выражение для функции    R^c . При выполнении дифференциальной связи в (3)

Rc (z, t, xc, uc ) = d^-. Тогда dt j Rcdt = j d^-dt = Y (z, tF, xF)- Y (z, ti, x|).

T ( z )            T ( z ) ^dt

С учетом этого, а также равенств х ( k , l , x_k ) = y l (т.е. выполнения сетевых связей) получим

N

I R k = YY ( y ( k , I , Ук ) -Y ( I , k , У 1 ) ) +

K ‘             K ‘ l = 1

+ Y ^c ( z , t i , x | ) - Y ( z , t F , x F ) + j ^ ^c ( z , t ) dt - I k ( y_k ) -

^T ( z )

- Y c ( z , t i , x c ) + Y ( z , t F , x F ) - j ^ ^c ( z , t ) dt .

^T ( z )

Тогда

N

I R k = ZZ Y ( k , l , Ук ) - Y ( l , k , У. ) ) - i k ( y k ).

K ‘             K ‘ l = 1

Окончательно имеем

L = - Zk\K' Rk - I Rk =

K '

NN

= ^- I ( y ( ^k , ^l , ^{x ( l} ) ) ^- y ( ^l , ^k , ^x ( ^k ) ) ) ⁺ I ⁱ k ⁽ Ук ) = ⁱ . k , l = 1                                                                 к = 1

Отсюда непосредственно вытекает следующая теорема.

Теорема 1. Пусть имеются последовательность дискретно- непрерывных элементов {ms} с D и пара (ф,фс) такие, что:

• 1)    ^ ^с ( z, t ) - кусочно-непрерывна при каждом z ;

• 2)    R ( k , x_s ( k ) , u s ( k ) ) ^ ^ ( k ) k g K \ K ‘ ;

• 3)    j ( R^c ( Z s ( k ), t , x ^ ( k , t ) , u_s ( k , t ) ) - n ( Z s ( k ), t ) — ^ 0, k g K'; T ( Z s ( k ) )

• 4)    G ( Z s ( k ), Y ( k ) ) - ц'( k ) ) ^ 0, k g K ‘ .

• 2.    Решение задачи для бассейна реки

Тогда { m s } - минимизирующая последовательность I на D .

Представим рассматриваемую модель распространения загрязнений в бассейне реки как ДНС, на верхнем уровне которой находится сеть (дерево) операторов, а на нижнем - система из уравнения (1) и уравнения dq = cr, q(0) = 0, dt где cr имеет смысл природоохранных затрат на единицу длины соответствующей камеры (здесь номер k также не указан).

Положим при k = 1,2,4 (операторы только со свободными входами):

x k = ⁽ x k , x²⁾ = const, p ⁽⁰⁾ = Ph = x k 1 ;

при k = 3,5:

xk = ⁽ xk 1 , xk 1 , xk 2 , xk 2 X pkI = xk 1 + xk 2 ^.

Сетевые связи выражаются следующим образом:

x 31 = У 1 , x 32 = У 2 , x 51 = У 3 , x 52 = У 4 .

Обозначим xc = (p, q)T, y = xc (tF), k = 1,. „, 5. Тогда рассматриваемая дифференциальная система и функционал Ik для каждой камеры запи шутся в виде

c

= A^cx^c + B^cu^c + s^c , 0 <  u^c = r g [0, p . ]. dt

I

I k C k x kF ,

Г—A 01       Г—11, „ .

где A^c =             B^c =      , s^c = ( s ,0) ^T , C k = [ (1 - P _k ) P _k ] .

L0   0JL

Здесь

9 ^(z , ^Y ) = Ук = x№ , ^{r c ( z} ) = ^{ Y ^{c :} t ki = ⁰, t kF = const, x_kI = K _kx_k ^},

^K k

1 0 1

1 0 1

, k = 3,5.

Оператор проектирования х (k , j , x ) x в данном случае - линейная функция: х ( k , j , x ) = ^ ( k , j ) x , ^ ( k , j ) — блочная матрица: Л ( к , 1) = [ E 0 ] , Л ( к ,2) = [ 0 E ] .

Функции ф и ф^с зададим линейными (с учетом линейности модели): ф ( к , l , У1 ) = V T ( k , l ) У1 ), Ф ^с ( k , t , x c ) = V ( к , t ) + V c ^T ( к , t ) x c .

Выпишем соответствующие выражения для G и R c , полагая ^ ^с = 0:

Rc = ycT (A (t)xc + Bc (t)uc + sc (t)) + уcTxc + Vc,

G = Z ( v T ( k , I ) x^c_ff — V T ( l , k ) Л ( к , l ) x ) + l

+ V ^{c T} ( ^{k ,0} ) ^K c x ^- V ^{c T} ( k , t kF ) ^xCf ^- C k x CF , n ( k , t ) = sup { R^c : u^c e U ^c ( k , t ) } = 0.

Согласно рассматриваемому графу будем иметь 5 функций ф^c нижнего уровня по числу дифференциальных операторов и 4 ненулевые функции ф верхнего уровня, соответствующие имеющимся сетевым связям, т.е. все у ( к , l ) равны нулю, за исключением у ( 1,3 ) , у ( 2,3 ) , у ( 3,5 ) , V ( 4,5 ) .

Из условий максимума R^c по x^c и u^c , G по x kF и x и ^ = 0 получаем

V ^c = - sup { V ^{c T} ( B^c ( к , t ) u^c + s^c ) : u^c e U ^c },

V ^c = - A ^T ( к , t) y ^c ( y ^{c 1} =- A ( k , t) y ^{c 1} , у ^{c 2} = 0 ) ,

V (k, tF ) = ^V (k, l)-CkT, KT Vе (к, t, ) = £ AT( k, l '^y (l, k).

ll

Последнее равенство должно выполняться для операторов с занятыми входами (номера k = 3,5). Конкретно для ненулевых значений у ( k , l ) :

yc (1, t1 F ) = у (1,3) - C10T, yc (2,12F ) = у (2,3) - C0T,

yc (3,13f ) = у (3,5) - C0T, уc (4,14f ) = у (4,5) - C0T, уc (5,15f ) = -C0T, kTуc (3,131) = AT (3,1)y (1,3) + AT (3,2)y(2,3),       (3)

K5Tуc (5,15f ) = AT (5,1)y (3,5) + AT (5,2)y (4,5), где Kk и AT(k, j) выписаны выше. После подстановки значений этих матриц получим у (1,3) = у (2,3) = (уc 1 (3,0), 0)T , у(3,5) = у(4,5) = (уc 1 (5,0), 0)T.

Из уравнений (3) получаем

V ^{c 1} = V ^c ’ ( t kF ) e^{A (} t ^kF - t ) , V ^c ’ ( k ,0) = y ^c * ( t F ) e^Atk F , y^{c 2} = const = - C ^02T =- в с , где

V^{е 1} ( 1 5 F ) = - (1 - в 5 ), v^c 1 ( t kF ) = - (1 - в 5 ) e A ⁵ F - (1 - P k ), k = 3,4, "  1 ( t kF ) = - ((1 - £ 5 ) e A ⁵ F + (1 - A)) e A ³ F - (1 - P k ), k = 1,2.

В итоге получаются конкретные значения ^ ( k , l ) и зависимости t// ^c ( t ). Оптимальные управления находятся из условия R^c , которое, очевидно, сводится к следующему:

( v c ² ( k , t ) C k - ^ 1 ( k , t ) ) r ^ max,

0SrSrk max т.е. управление будет кусочно-постоянным со значениями 0 либо rk max в зависимости от знака функции переключения t//c2(k, t)ck - ^ 1(k, t), которая, как видно, зависит от весов в. Последние подбираются так, чтобы для соответствующих распределений загрязнений по руслам выполнились заданные ограничения. При этом получаются следующие конкретные выражения для функций переключения Mk(tk):

M 5 ( t 5 ) = (1 - £ 5 ) e A ⁽ t ⁵ F - t 5 ) - P s c ₅,

M_k ( t_k ) = (1 - P _k ) e^{A (} t ⁵ F ⁺ t F - t k ) - p k c k , k = 3,4,

M_k ( t_k ) = (1 - P k ) e^{A (} t ⁵ F ⁺ t ³ F ⁺ t kF - t k ) - P k c k , k = 1,2.

Были проведены расчеты для условного бассейна, близкого по характеристикам к нижней части бассейна р. Селенги – главного притока оз. Байкал. Данные для расчетов содержатся в таблице.

Таблица

№	tF	A	c , млн руб. км 4 /т	s , т/км 4	pI , т/км 3	Г . max , т/км 4
1	20	2.5 х 10 - 3	4 х 10 2	0.5 х 10 - 2	0.4	0.6 х 10 " 2
2	30	3 х 10 - 3	10 3	0.2 х 10 - 2	0.3 х 10 " 1	0.25 х 10 " 2
3	30	2.5 х 10 - 3	7 х 10 2	0.3 х 10 - 2	-	0.35 х 10 " 2
4	20	3 х 10 - 3	10 3	0.2 х 10 - 2	0.4 х 10 " 1	0.25 х 10 " 2
5	150	2.5 х 10 - 3	4 х 10 2	0.5 х 10 - 2	-	0.6 х 10 " 2

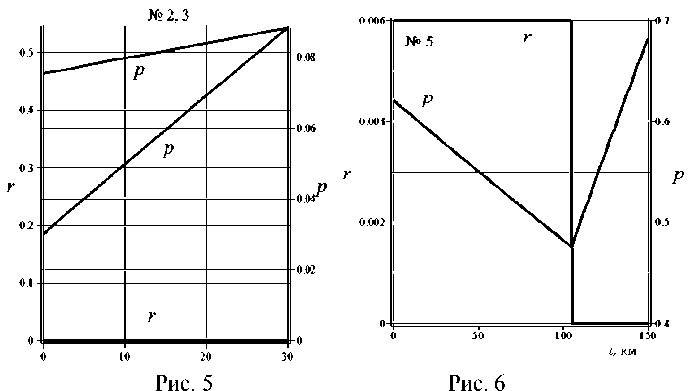
Значения весов P _k задавались равными: e k = в . В этом случае непосредственно видно, что всюду r_k = 0, Q = 0 при в = 1, т.е. затраты отсутствуют, а загрязнение максимально, а при в = 0 r_k = r_{k max}, т.е. интенсивность очистки всюду максимальна. Результаты расчетов для промежуточных значений в представлены на рис. 4-6.

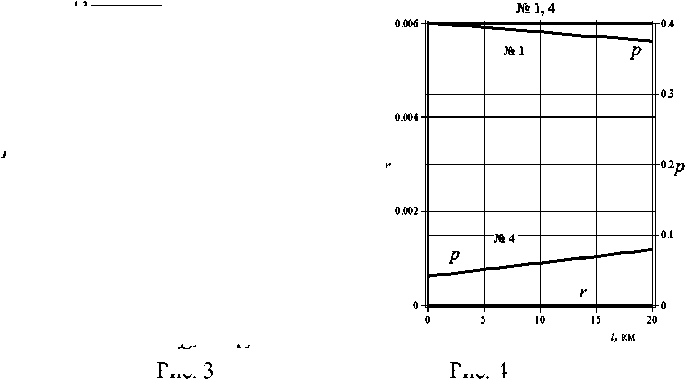
Рис. 3

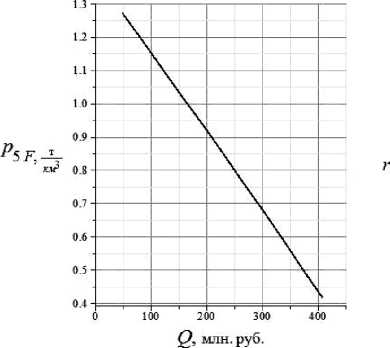
Рис. 4

Зависимость p _{5 F} ( Q ) (рис. 3) служит для выбора варианта стратегии природоохранной деятельности с учетом располагаемых ресурсов.

На рис. 4–6 показаны распределения управляющих воздействий r_k ( t ) и соответствующих концентраций загрязнений p ( t ) во всех камерах при заданном значении суммарных затрат Q = 300 млн руб. Видно характерное свойство оптимального решения при рассматриваемом критерии: экономия ресурсов производится в первую очередь за счет прекращения природоохранной деятельности на конечных участках бассейна (в данном случае – во всей камере 4 и на последних 45 километрах в камере 5), что по смыслу означает рациональное использование самоочищающей способности, представленной коэффициентом A .

Заключение

Описанная двухуровневая модель распространения примесей в бассейне реки на основе абстрактной сети операторов является новым шагом на пути иерархического представления систем неоднородной структуры – от чисто динамических к более общему классу систем сетевой структуры. Эта модель позволяет эффективно решать соответствующие сложные задачи оптимизации по принципу декомпозиции на однородные подсистемы и задачи, к которым применимы известные методы теории оптимального управления, ставшие уже классическими.

Упрощенное описание моделей нижнего уровня выбрано лишь для иллюстрации общего подхода; на самом деле он сохраняется и для значительно более сложных описаний, рассматриваемых при решении конкретных практических проблем, связанных с эффективным планированием водоохранных мероприятий как частью общей стратегии устойчивого развития соответствующей природной территории, например, такой как Байкальский регион.