Моделирование заданного движения пятизвенного механизма

Исследованию движения многозвенных механизмов посвящено большое количество литературы [1, 2, 3]. Актуальной является задача моделирования заданного движения механизма.

В данной работе излагается подход моделирования заданного движения пятизвенного механизма с привлечением нечетких алгоритмов. Рассматривается задача о компьютерном моделировании пятизвенного механизма с помощью пакета программ моделирования физических законов и задача управления моделью с помощью системы нечетких правил [4, 5].

1. Уравнения движения

Рассмотрим пятизвенный механизм, изображенный на рис. 1.

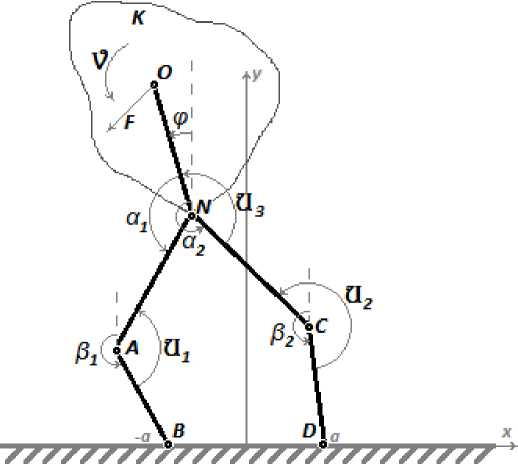
Рис. 1. Пятизвенный механизм

На этом рисунке точки A, N, C – точки шарнирного соединения невесомых стержней BA, AN, DC и CN. Центром масс тела K является точка O.

Внешние силы, приложенные к телу K, приведены к одной силе F = (X, Y), приложенной в центре масс, и к паре сил с моментом V. Посредством U i (i=1, 2, 3) обозначены управляющие моменты в шарнирах. Посредством α 1 , α 2 , β 1 , β 2 обозначены углы, которые образуют стержни с вертикальной осью. Длины этих стержней обозначим AN=CN= l , BA=DC= L . Угол, который образует отрезок ON с вертикальной осью, обозначим буквой φ. Точки B и D неподвижны и их координаты равны соответственно (-a, 0), (a, 0). Здесь число a>0.

В качестве обобщенных координат возьмем координаты точки N. Тогда из условия неподвижности точек B и D получим уравнения связей х — I sin aT — L sin 8t = —а, у + I cos aT + L cos 8t = 0, x — I sina2 — Lsin82 = a, y + lcosa2 + Lcos82 = 0-

Кинетическая энергия тела K равна

T = у (X ² + y ² ) — mpy(X cosy + y siny) + - y ² .                 (2)

Здесь обозначено m - масса тела K, J=J o +mp ² , p - длинна отрезка NO, J o - момент инерции тела K относительно центра масс.

Используя равенства x0 = x —psiny, y0 = y + pcosy, запишем элементарную работу сил на возможных перемещениях

6Л = XSx + YSy + (V + U ₃ — pX cos y — pY sin y)Sy + +(U i — U ₃ )5_{a i} + (U — U ₃ )5« 2 — U 1 68 1 — U 2 ^^ 2 -

Выразим возможные изменения ба, и бв/ через бх и бу с помощью формул (1). Полу чим бЛ = Qx бх + Qy Sy + Q^ бу, где обобщенные силы равны х + а             х — а            sin ^2

^Q ' = ^X " ^U 1 ILsin^ i —8 1 ) " ^U2 l.sin„ 2 -^ 2 ) ^{+ U} = ls-n(« 2 -^ 2 )’

У                 У              cos 8 ₂

^Q _y    V U_T iLsin(_{a i} — 8 _t ) ^² lLstn(a ₂ — 8 ₂ )   ^³ lstn(a ₂ — 8 ₂ ),

Q ^ = V + U ₃ — pX cos y — pY sin y.

Используя формулы (2) и (3), запишем уравнения Лагранжа d dT dT d"td^ — d^ = Q^'    q = X'y'y-

Моделирование заданного движения пятизвенного механизма Они принимают вид х — рф cos ф + рф2 sin ф = — Qx, у — рф sin ф — рф2 cos ф = — Qy,

ф

—р                1

— — (х cos ф + у sin ф ) = - Q y .

Из первых двух уравнений выразим величину х cos ф + у sin ф и подставим в третье уравнение. Получим

Q y + р(Q x cos ф + Q y sin ф)                                (5)

Подставим эту формулу в первые два уравнения (4). Получим х + рф2 sin ф = ^j- cos2 ф +—^ Qx + -р sin ф cos фQy + —■ cos ф Qy, у — рф2 cos ф = рр sin ф cos ф Qx + ^р sin2 ф +—^ Qy + р sin ф Qy.

• 2.    Моделирование заданного совместного со связями движения

  • 2.1.    Описание алгоритма построения управления

• 2.2.    Моделирование прямолинейного и равномерного движения точки N

Пусть заданы функции x(t), y(t), которые совместны со связями (1). Подставляя третью формулу (3) в третье уравнение (4) получим, что ф = ~ (x(t) cos ф + y(t) sin ф) + J (У + U3 — рХ cos ф — рY sin ф).         (7)

Допустим, что мы построили управнение Us(t, ф, ф), которое обеспечивает заданный закон ф(t) изменения угла ф. Определитель матрицы, составленной из коэффициентов, стоящих в формулах (6) перед Qx и Qy, равен ——+ Д; > 0. Поэтому из формул (6) 4                                   Jom mz                                     4

находим Qx(t, ф, ф) и Qy(t, ф, ф). Подставляя эти выражения в формулы (3), находим моменты Ui(t, ф, ф), i=1, 2, 3. Отметим, что определитель матрицы, составленной из ко- эффициентов, стоящих в формулах (3) при переменных U1 и U2, равен

—--- ^У ---— ^ 0 при y ^ 0, a i ^ e i .

sin(a ₁ -^ ₁ )sin(a ₂ -^ ₂ )                     ^г

Рассмотрим случай, когда x(t) = y(t) = 0. Из формул (6) и из третьей формулы (3) получим, что

Q _x = р—ф ² sin ф +

р ² — "Г

(Х cos ф + Y sin ф) cos ф

р—

— — (У + U ₃ ⁾ cos ф ,

"      p ² m                     pm

Q _y = —pmф ² cos ф H—j— (X cos ф + Y sin ф) sin ф —— (V + U ₃ ) sin ф.

Подставим эти выражения в формулы (3). Найдем управляющие моменты

U ₁ = IL(A ₁ + B ₁ U₃)sin(a ₁

U 2 = IL(A2 + B 2 U ₃ )sin(« 2

B 1 ), ^ 2 ).

Здесь обозначено

^ 1

= ^— |уХ — (% — a)Y — (у sin ф + (% — a) cos ф)pmф ²

^ 2

2ау

pm                                       1

+ -у (у cos ф — (% — a) sinф)(V — pX cos ф — pY sinф)j,

—yX + (% + a)Y — (у sin ф + (% + a) cos ф)pmф ²

pm                                       1

—— (у cos ф — (% + a) sinф)(V — pX cos ф — pY sinф)j,

B 1

у sin B ₂ + (% — a) cos B ₂

2aZy sin(a ₂ — ^ ₂ )

pm

+ -у (у cos ф — (% — a) sin ф),

B 2

у sin B ₂ + (% + a) cos B ₂ pm

2alysin(_a 2 —^ 2 ) --— ⁽yc^osV-⁽% + ^a)sinv)-

Уравнение (7) в рассматриваемом случае принимает вид ф = J (V — pX cos ф — pY sin ф) + J U3.

Рассмотрим случай, когда X=0, Y=–mg, V=0. Тогда уравнение (10) записываем в следующем виде:

pmg 1

ф = "у sinф + yU3.

Если моделируем ф(£) = 0, то в формулах (9) можно положить sinф ~ ф, cosф ~ 1, sin ² ф ~ 0. Они примут вид

1           x z             x . p2m2      1

^Л 1 = 2оу I (% — a)m^ — (уф + % — a)pmф ² +      дуф I,

Л 2 =    1 — (% + a)mg — (уф + % + a)pmф ² — ^P-^m-gyфI,

2оу [                                        /       ]

B 1

у sin B ₂ + (% — a) cos B ₂

2aZy sin(a ₂ — ^ ₂ )

pm

+ — (У — (% — а)ф),

B 2

у sin B₂ + (% + a) cos B₂ pm L-_a^______£.^—^у^+ом

• 3.    Создание системы управления

  • 3.1.    Среда для физического моделирования

• 3.2.    Принципы управления

В работе была создана среда для физического моделирования поведения механизма и визуализации работы системы. Для этого был использован пакет компьютерного моделирования физических законов реального мира Box2D. Этот пакет также имеет средства графического отображения объектов.

Для начала рассмотрим перемещение точки N. Для изменения положения точки N достаточно использовать U 1 и U 2 . Все возможные положения точки N будут находиться в заштрихованной зоне на рис. 2.

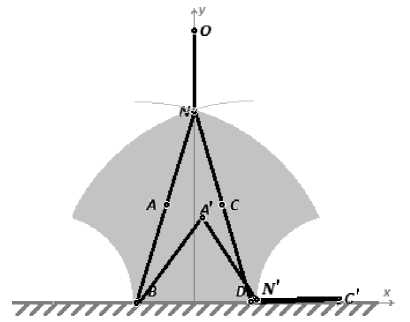
Рис. 2. Возможные положения точки N

Верхние граничные положения достигаются, когда ^ BAN = ^ DCN = 180° и лежат на соответствующих дугах с радиусом |BA|+|AN|. При условии, что звенья не могут проходить сквозь опору и сквозь друг друга, нижние границы также будут образованы дугами, когда точка C либо точка A лежит на оси абсцисс. Радиус дуг будет соответственно |CN|.

Для уменьшения координаты y точки N необходимо, чтобы U 1 <0 и U 2 >0. Если N находится не дальше a по оси x, то для отклонения в сторону положительных x необходимо N приближать к точке D. Это достигается при U 2 >0.

Так как точку N можно переместить в любую соседнюю точку внутри области, то мы можем перемещать ее по любой траектории внутри области.

Возможное положение точки O относительно точки N задается простой окружностью с радиусом |ON|. Углы α можно изменить при помощи U 3 .

• 3.3.    Построение системы управления

В ходе работы изначально была создана пробная системы управления звеньями механизма, обеспечивающая грубое управление. Впоследствии при анализе поведения построенной системы управления и выявлении недостатков управления, вносились изменения в нечеткие правила для того, чтобы траектория была максимально приближена к заданной.

В математической модели звенья не имели толщины и массы, но для большей реалистичности модели звенья были заданы тонкими прямоугольниками с малым весом. В точке O было добавлено жестко закрепленное тело с заданной массой. На каждом шаге моделирования для каждой пары объектов обрабатываются столкновения и силы взаимодействия.

В качестве среды программирования использована Embarcadero Delphi XE2.

Система управления, построенная на основе нечеткой логики, создавалась на экспериментальных данных, получаемых в ходе исследования движения модели.

Нечеткие правила и функции принадлежности составлены в системе FuzzyTECH 5.54 [6]. При фаззификации использован стандартный метод фаззификации (Compute MBF). Он предполагает использование функций принадлежности стандартного типа – треугольных, трапециевидных и кусочно-линейных кривых. Для агрегирования подусловий правил нечетких продукций использовано правило минимума.

Для дефаззификации выходных переменных U 1 , U 2 и U 3 используем стандартный метод (Center_of_Maximum или сокращенно СоМ), который, по мнению разработчиков FuzzyTECH, представляется методом наилучшего компромисса для получения окончательного значения выходных переменных.

Программа составлена таким образом, что в процессе работы можно с помощью клавиатуры или мыши вносить дополнительные помехи. При этом система управления адекватно реагирует на все изменения и корректирует траекторию движения.

Заключение

Реализованная в работе модель, как, впрочем, и система управления – это лишь приближения к реальности. При реализации реальной системы управления реальным механизмом необходимо будет учесть еще ряд различных особенностей, условий и ограничений. Например, здесь предполагалось, что скорость поворота конечности можно изменять мгновенно, устанавливая ее равной заданной, но так, чтобы она не превышала максимальную. Это лишь приближение, на самом же деле, для любого реального привода, каков бы он ни был, существует более сложная зависимость его ускорения от скорости, внешнего сопротивления и внутреннего воздействия.

Однако, несмотря на неизбежные отличия модели от реального объекта, данная работа продемонстрировала возможность создания системы управления и показала путь к созданию такой системы – исследование поведения модели, накопление опыта управления, и изменение системы управления на основе полученного опыта.

В дальнейшем, возможно, будет попытка реализации модели пятизвенного механизма с незакрепленными к поверхности нижними звеньями. Это позволит реализовать походку пятизвенного механизма.