Модельный аудит региональной стратегии: анализ согласованности целевых показателей

DOI:

Цитирование. Патракеева О. Ю., Скороходов В. А., 2020. Модельный аудит региональной стратегии: анализ согласованности целевых показателей // Региональная экономика. Юг России. Т. 8, № 1. С. 101–116. DOI:

Постановка проблемы

В настоящее время наблюдается повышенное внимание региональных властей к определению средне- и долгосрочных задач развития. В связи с этим применение методов стратегического управления выступает обеспечительным условием успешного развития социально-экономических процессов на уровне субъектов Российской Федерации [Ускова, 2004; Иншаков, Митрофанова, 2009].

Обеспечение устойчивого развития и территориальной целостности, повышение качества жизни населения являются ключевыми целями региональных пространственных стратегий и планов [Nogues, Gonzalez-Gonzalez, Cordera, 2019]. Для определения эффективности плановых мероприятий по выполнению стратегий применяются системы оценки и мониторинга, основанные на использовании различных показателей [Hatakeyama, 2018]. Кроме того, в работе [Vecchiato, 2019] показано, что индикативное сценарное планирование способствует положитель- ной динамике долгосрочных инвестиций в условиях нестабильности.

Стратегии социально-экономического развития субъектов России представляют собой основополагающие документы, отражающие векторы, ориентиры и приоритетные направления, качественные и количественные характеристики средне- и долгосрочного развития регионов, исходя из сложившихся тенденций и достигнутого уровня. В связи с этим стратегические цели их развития должны быть сформированы системно. Зачастую в стратегических документах эталонное состояние региональной системы описывается общими формулировками либо перечнем отдельных сценарных показателей, целевые значения которых должны быть достигнуты в долгосрочной перспективе. Довольно распространенной является практика включения в стратегии показателей, целевые значения которых приводятся вне привязки к другим индикаторам экономического развития региона. Соответственно, взникает вопрос о согласованности и достижимости целевых показателей к определяемому в стратегиях периоду.

Серьезной проблемой формирования и развития системы стратегического планирования является отсутствие единой системы показателей, основанной на международных и российских стандартах национального счетоводства [Сурнина, Шишкина, 2013]. Однако логика включения тех или иных целевых показателей и тем более причинно-следственные взаимосвязи между ними не раскрываются. Ключевые секторы экономики, или так называемые точки роста, выявляются несистемно, следовательно появление синергетического эффекта от их совместного развития маловероятно [Лапыгин, 2014].

В связи с этим поиск источников долгосрочного роста экономики региона должен основываться на системном анализе текущего состояния того или иного субъекта и динамики его развития в разрезе видов экономической деятельности, определении влияния структуры инвестиций в технологии [Сухарев, 2019; Berezinskaya, 2017], поскольку формальный рост отдельных целевых показателей, не подкрепленных улучшением качественных характеристик, приводит к разрушению хозяйственных связей и падению уровня жизни населения.

Для целей прогнозирования и количественного анализа экономического роста широко применяются методологические подходы, заключающиеся в построении агрегированных производственных функций, авторегрессионных моделей [Горидько, Нижегородцев, 2012; Ко-ломак, 2011; Осиневич, 2015; Андреев, 2016]. Однако для определения согласованности и достижимости индикаторов, представленных в стратегиях, необходима разработка более точных количественных моделей, учитывающих волатильные характеристики временного ряда, например нелинейно распределенную во времени отдачу от капиталовложений, влияние фактора времени, и позволяющих формировать максимально обоснованные прогнозы на базе внутренних взаимосвязей в структуре фактических тенденций регионального развития.

Цель настоящей статьи – продемонстрировать возможности проверки системной взаимосвязи и согласованности ключевых экономических индикаторов региона на основе применения соответствующих аналитических инструментов моделирования временных рядов. Процедуру данной проверки представляется возможным обозначить как «модельный аудит». Смысл данного определения предполагает верификацию фактически заложенных модельных предпосылок целевых покзателей.

В качестве объекта анализа рассмотрим «Стратегию социально-экономического развития Ростовской области до 2030 года».

Методология исследования

Современные условия диктуют необходимость технологической модернизации хозяйственного комплекса, импортозамещения, способного обеспечить повышение конкурентоспособности промышленного и сельскохозяйственного производства. Решение данных задач предполагает увеличение инвестиций в основной капитал экономики страны и ее регионов [Кабанов, Жильников, Заблоцкая, 2018]. Соответственно, объем инвестиций в основной капитал в Стратегии развития Ростовской области включен в состав ключевых индикаторов наравне с валовым региональным продуктом (ВРП) и среднедушевыми денежными доходами населения (табл. 1).

Необходимо отметить, что применение исключительно корреляционно-регрессионного анализа временных рядов представляется нецелесообразным. Для моделей сложных систем, в частности экономических, исключительно регрессионная идентификация коэффициентов связи между переменными может приводить к искаженным прогнозам. Исследователи [Затонский,

Таблица 1

Экономические индикаторы реализации Стратегии Ростовской области при целевом сценарии

Показатель	2017 г.	2021 г.	2024 г.	2030 г.
ВРП (в текущих ценах), млрд руб.	1 344,0	1 763,9	2 194,5	3 828,3
Инвестиции в основной капитал (в текущих ценах), млрд руб.	319,3	344,4	476,2	916,1
Среднедушевые денежные доходы населения, руб.	27 677,0	39 791,5	54 028,7	99 696,7

Примечание. Составлено по данным: [Стратегия социально-экономического развития ... , 2018].

Янченко, 2014; Zatonskiy, Safyanova, 2016; Быст-рай, Лыков, 2014; Трегубова, 2016; Миронов, Худякова, Благинин, 2017] приходят к выводу, что в некоторых эконометрических моделях использование в качестве основы дифференциальных уравнений позволяет получить более надежные результаты за счет возможности описания положительных и отрицательных изменений динамики от воздействия рассматриваемых факторов, а также возможности получения асимптотических решений.

Для выполнения настоящего исследования с учетом специфики исходных данных выбраны следующие элементы научного анализа: аналитические методы формирования и решения дифференциальных уравнений, описывающих экономическую динамику ключевых показателей развития на уровне региона; корреляционный анализ статистических данных основных социально-экономических показателей региона в динамике за 2000–2017 гг.; формально-логический анализ модельных и целевых показателей.

В целом же применение отмеченных аналитических инструментов позволяет провести аудит согласованности ключевых параметров региональных стратегий путем сверки целевых показателей стратегии с модельными результатами.

Анализ критичности полученных отклонений по итогам проведения соответствующих сопоставлений, а также взаимосвязи отклонений отдельных целевых покзателей может являться ключевым аналитическим блоком модельного аудита. Его исполнение может указывать на наличие или отсутствие системных противоречий в закрепленных Стратегией количественных показателях целевых сценариев.

Результаты исследования и их анализ

Инвестиции в основной капитал оказывают долгосрочный эффект на развитие региона [Юсупов и др., 2019]. Они выступают основным регулятором экономической динамики, способным как стимулировать ускорение ее темпов, так и формировать причины, сдерживающие экономический рост [Полянин, 2011]. Таким образом, именно соотношение «Инвестиции в основной капитал – ВРП» является ключевым и требующим проверки на согласованность и системность подхода к совместному прогнозированию двух целевых индикаторов.

Для взаимосвязи трендов показателей «Инвестиции в основной капитал» и «Валовой регио- нальный продукт» выделим следующие характеристики:

– динамика инвестиций более волатильна, чем динамика ВРП. Темп роста инвестиций превышает темп роста ВРП: CAGR 2 (индекс инве-стиций)2000–2017= 109,1 %; CAGR (ВРП)2000–2017 = 106,1 %;

– тренд инвестиций подвержен циклическим корректировкам, связанным с влиянием мировой конъюнктуры (2009–2011 гг.), восстановлением инвестиционной активности (2012–2015 гг.), периодом завершения предыдущего инвестиционного цикла в 2016 г. (ввод в эксплуатацию крупных проектов, в частности третьего энергоблока Волгодонской АЭС) и началом нового (реализация инфраструктурных проектов в рамках подготовки к Чемпионату мира по футболу 2018 г.);

– снижение динамики индекса инвестиций не сопровождается синхронным снижением в динамике ВРП ввиду эффекта высокой базы, распределенного во времени, и мультипликативного эффекта крупных инвестиционных проектов, реализуемых на территории Ростовской области.

Отмеченные характеристики временных рядов инвестиций и ВРП указывают на повышенную волатильность, преимущественно на стороне влияющего фактора, нелинейный характер связи зависимой и влияющей переменной и возможные лаговые эффекты воздействия, распределенные во времени за несколько периодов.

Таким образом, для целей учета комплексной специфики влияния инвестиций на ВРП с учетом распределенных во времени эффектов целесообразно рассмотреть дифференциальную модель изменения отдачи от инвестиций. Соответственно, решение данного уравнения должно специфицировать форму влияния инветиций на ВРП с учетом распредленных во времени эффектов.

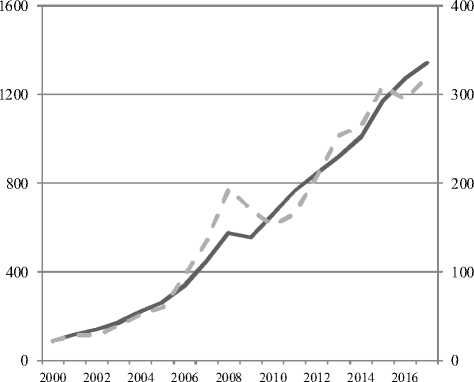
Для спецификации целевой дифференциальной модели и ее решения рассмотрим первичную математическую модель изменения ВРП (далее функция y ( t )) в зависимости от совокупного объема инвестиций, осуществленных как в текущем году, так и в предшествующие периоды (далее функция x ( t )). Учет временного фактора реализуем через допущение распределенного во времени влияния инвестиций в основной капитал. С учетом проведенного анализа временных рядов (рис. 1) предполагается влияние инвестиций не только на ВРП в году их осуществления, но и на ВРП в последующие периоды времени.

Ввиду наличия фактора износа основных фондов, определяющего тенденцию к снижению отдачи на вложенный капитал, целесообразно ввести соответствующие весовые коэффициенты для периодов t + n относительно периода капитальных вложений. Для моделирования подобного поведения переменной x ( t ) введем дискретную весовую функцию c ( t ), где t е [1; n ] Z и n - количество периодов значимого влияния инвестиций, осуществленных в году t . Отметим, что в качестве весовой функции может быть рассмотрена функция произвольного вида, удовлетворяющая следующим условиям:

C ( t 1 ) < c ( t 2 ) , если 1 1 <  1 2 ⁶ [ 1 n ] z ; n

|            2 c ( k ) = i.                       (1)

k = 1

Принимая во внимание нелинейный характер влияния инвестиций на ВРП (рис. 1), для рассматриваемой модели выбран следующий вариант весовой функции, удовлетворяющей (1):

c ^{( k} ) = 2k^^{1 v k 6} [ 1; n ^] z .               (2)

n ²

Величина x ( t ) определяется по правилу:

x ( 1 ) = £ c ( k ) • Inv ( 1 - n + k ),                (3)

k = 1

где Inv( t – n + k ) – объем инвестиций в основной капитал в году ( t – n + k ).

Рассмотрим функцию вида (4):

f ⁽ t )=^p^^k)- t ' •                   (4)

где значение параметра p положительно. Данная функция отображает отдачу ВРП на вложенные инвестиции в основной капитал, скорректированную на тренд ее изменения ( t_q ). Таким образом, можно полагать, что скорость ее роста пропорциональна самой величине f ( t ) и с учетом времени имеет следующий вид:

df^¹ ) = ⁽ C 1 • ¹ + c 2 ) • f ^{( 1} )-                 (5)

dt

Отметим, что дифференциальное уравнение (5) является уравнением с разделяющимися переменными, следовательно может быть преобразовано к интегральному уравнению (6):

J T1 y = i ⁽ c 1 • ^{1 +} c 2 " d¹ -                (6)

Интегрируя левую и правую части, получаем соотношение (7), описывающее зависимость величины y ( t ) от времени:

Inf ( 1 ) = a • 1 ² + b • 1 + c ,                    (7)

c где a = -^,b = c2.

Таким образом, из соотношений (4) и (7) получим основное уравнение модели вида (8), описывающее зависимость величины ВРП от

ВРП, млрд рублей

Инвестиции в основной капитал, млрд рублей

Рис. 1. Динамика изменения валового регионального продукта и инвестиций в основной капитал по данным 2000–2017 гг.

Примечание. Составлено авторами.

совокупных инвестиций текущего и предшествующего периодов:

y ( t ) = e“ t 2 ⁺ bt ⁺ c - t - q - x p ( t ) .                    (8)

Отметим, что величины a , b , c , p и q являются неизвестными параметрами. Для их нахождения применим метод максимального правдоподобия [Воронов, 2016]. Для этой цели введем в рассмотрение аддитивную ошибку ^ , полагая, что она распределена по нормальному закону с нулевым математическим ожиданием. Таким образом, с включенной ошибкой £ в соотношении (9):

y ( t ) = e ^a • ^{1 2 +} b • ^{t +} c . t - q - x p ( t ) + ^                  (9)

требуется определить коэффициенты a , b , c , p и q так, чтобы функция правдоподобия достигала максимума (10):

^ y ( t ) - e at ^{2 +} b . " ⁺ c -t - q - x p ( t ) }

F ( a , b , c , d , p , q ) = П ^e        2 ' °                ⁽¹⁰⁾

t

Построим функцию G ( a , b , c , p , q ) = lnF( a , b , c , p , q ). Отметим, что поскольку логарифм является монотонной функцией, следовательно максимум функции G совпадает с максимумом функции F . Произведя необходимые вычисления, получим, что максимум функции (11):

( y ( t ) - e ^{a - t} 2 ^{+ b} t ^{+ c} - t" ^q - x ^p ( t ) ) 2

2-°

G (a, b, c, d, p, q )= V t=2000

достигается при следующих значениях параметров:

n = 7; a = 0,256 · 10^-5; b = 0,06; c = -34,94; p = 0,47; q = 11,44.

Следует отметить, что, согласно рассматриваемым данным, для Ростовской области оптимальным количеством периодов значимого влияния инвестиций является величина n = 7.

Таким образом, подставив значение n = 7 в выражения (2) и (3), получим вклад (или «вес») каждого года из семи лет в совокупные инвестиции:

/ x 2-1-1        / x 2-2-1

c ( 1 ) = —= 0,02; c ( 2 ) =---= 0,06;

72                     72

/ x 2-3-1        / x 2-4-1

c ( 3 ) = -y2- = 0,10; c ( 4 ) = -2-;

c ( 5 ) = 2.5^ = 0,18; c ( б ) = 27 ^{- 1} = 0,22;

c ( 7 ) = 2.7^ = 0,27.

Следовательно, совокупные инвестиции вычисляются следующим образом:

x ( t ) = ]T c ( k ) - Inv ( t - 7 + k ) = 0,02 - Inv _t - 6 + 0,06 - Inv _t - 5 + + 0,10 - Inv _{t - 4} + 0,14 - Inv _{t - 3} + 0,18 - Inv _{t - 2} + 0,27 - Inv _t .

Вычисленные веса указывают на убывающую отдачу от инвестиций во времени.

Проводя сравнение отклонений расчетных значений y ( t ) от наблюдаемых, вычислим среднюю ошибку аппроксимации по формуле (12):

₅ = 1 - V I y t y ^{( t )} -100 %, b ^7"     У,

где m – число сравниваемых значений, получим 5 = 3,75 %.

Таким образом, модель вида (8) адекватна и может применяться для целей экономического анализа отдачи от инвестиций в основной капитал для Ростовской области.

Для проверки согласованности и достижимости целевых показателей Стратегии апробируем разработанную математическую модель на данных, соответствующих целевому сценарию Стратегии региона и представленных в Прогнозе долгосрочного социально-экономического развития Ростовской области до 2030 г. [Прогноз ... , 2018] (см. табл. 2).

Проведем экономический анализ полученных результатов:

• 1.    В случае расчета ВРП по модели (9) его уровень при целевом объеме инвестиций в основной капитал (табл. 2) должен выйти на большую величину и составить к 2024 г. – 2 521,5 млрд руб., к 2030 г. – 4 884,3 млрд рублей. Согласно Стратегии, ВРП к 2030 г. составит 3 828,3 млрд рублей. Следовательно, для достижения целевого уровня ВРП при сохранении сложившихся пропорций экономического роста необходим меньший объем инвестиций.

• 2.    Согласно модельным расчетам, неинфляционный прирост ВРП (в сопоставимых ценах) при прогнозируемом объеме инвестиций должен составить 7,8 % к 2030 г., однако в Прогнозе Правительства Ростовской области рост ожидается на уровне 6,7 % (рис. 2).

Фактически же заложенный в Стратегии Ростовской области прогнозируемый уровень ВРП предполагает значительное снижение отдачи от инвестиций. Теоретически данный сценарий представляется возможным в случае увеличения горизонта отдачи от инвестиционных вложений на территории региона. Кроме того, снижение отдачи от капиталовложений в Ростовской области может быть обусловлено тем, что реализация инвестиционной политики осложняется рассогласованием между первоочередными (условно – инфраструктурными) и рыночными потребностями ключевых отраслей экономики региона. Данная проблема характерна и для других субъектов Российской Федерации [Конище-ва, 2014].

Вместе с тем обоснование и спецификация условий неявно заложенного сценария снижения не приводятся, а его логика, без должной верификации значимых факторов, противоречит первоочередным целям Стратегии, таким как: «формирование новейшей технологической базы, создание высокопроизводительных рабочих мест, развитие высококонкурентоспособной промышленности, модернизация инфраструктуры». С точки зрения общеэкономической логики специфика данных целей предполагает, напротив, рост отдачи на вложенный капитал и интенсификацию производства.

Актуальная концепция качественного экономического роста, основанная на развитии конкурентных преимуществ региона, предполагает стимулирование инвестиционных вложений, в том числе

Таблица 2

Сопоставление целевого прогноза Правительства Ростовской области и прогноза по модели (в текущих ценах), млрд руб.

Год	Инвестиции в основной капитал	ВРП (целевой прогноз)	ВРП (модельный прогноз)
2018	296,2	1 424,4	1 508,1
2019	310,4	1 529,7	1 625,1
2020	327,3	1 641,6	1 753,8
2021	344,4	1 763,9	1 896,4
2022	376,8	1 893,8	2 066,4
2023	420,5	2 037,4	2 272,4
2024	476,2	2 194,5	2 521,5
2025	528,5	2 388,7	2 807,4
2026	587,6	2 608,0	3 131,2
2027	654,6	2 857,5	3 496,3
2028	731,3	3 139,0	3 906,9
2029	817,7	3 458,6	4 367,3
2030	916,1	3 828,3	4 884,3

Примечание. Составлено авторами.

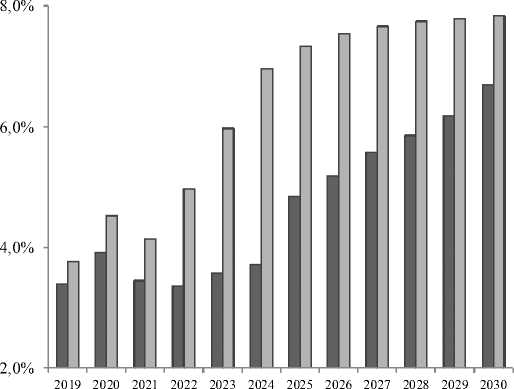
• □    Прогноз Правительства

• □    Модельный расчет

Рис. 2. Темпы прироста ВРП в сопоставимых ценах

Примечание. Составлено авторами.

в сегменте транспортной инфраструктуры для устранения инфраструктурных ограничений роста экономики. В частности, согласно Стратегии развития Ростовской области до 2030 г., инвестиции в реконструкцию и модернизацию транспортной инфраструктуры являются приоритетным направлением пространственной политики.

В связи с подготовкой Ростова-на-Дону к проведению Чемпионата мира по футболу 2018 г. реализованы крупные инфраструктурные проекты, а именно: построена новая транспортная развязка автомобильной дороги М-4 «Дон» Южный подъезд к Ростову-на-Дону, введены в эксплуатацию развязки над существующей трассой. В настоящее время приоритетными проектами являются строительство обхода г. Аксая, а также третьей очереди Северного обхода, реконструкция существующих магистралей Ростовской агломерации.

Реализация крупных транспортных проектов призвана обеспечить растущие потребности в грузоперевозках региона. Динамической целью Стратегии Ростовской области является обеспечение потребности грузооборота транспорта с приоритетом безопасности транспортного сообщения к 2024 г. – до 60,0 млрд т • км, к 2030 г. – до 65,5 млрд т • км. Цель реализуема при условии роста капиталовложений в развитие инфраструктуры и производящих секторов, которые и предъявляют спрос на грузоперевозки.

Для анализа взаимосвязи трендов показателей «Инвестиции в основной капитал» и «Грузооборот транспорта общего пользования» выделим следующие характеристики за период 2007–2017 гг.:

– чувствительность грузооборота по инвестициям в среднем за рассматриваемый период невысока, темп роста инвестиций превышает темп роста грузооборота: CAGR 2 (индекс инве-стиций)2007–2017 = 104,5 %; CAGR (Грузообо-рот)2007–2017= 102,3 %;

– тренд грузооборота не подвержен циклическим колебаниям, в отличие от тренда инвестиций, и менее волатилен. Коэффициент вариации грузооборота меньше, чем индекса инвестиций – 9,5 % против 13 %;

– снижение динамики индекса инвестиций не сопровождается аналогичным синхронным снижением в динамике грузооборота ввиду зависимости последнего от объемов отгрузки произведенных товаров, среднего расстояния перевозок. Грузооборот подвержен существенным лаговым нелинейным эффектам – его изменение носит частично «пороговый характер»: в 2009–2013 гг. резкий рост инвестиций сопровождается замедленным ростом грузооборота до уровня его условной стабилизации. Прирост инвестиций в 2009–2013 гг. составил 49 % против прироста грузооборота на уровне 19 % за тот же период.

Отмеченные характеристики временных рядов инвестиций и грузооборота указывают на нелинейный характер связи и возможные лаго-вые эффекты воздействия, распределенные во времени за несколько периодов (рис. 3).

Принимая во внимание результаты совместного анализа временных рядов инвестиций и грузооборота, указывающих на наличие предположительно существенных нелинейных эффектов, введем в рассмотрение следующую функцию f ₁( t ), характеризующую отдачу в размерности объема грузооборота (млн т • км) на 1 млн руб. инвестиций, взвешенную согласно допущению (2) за период 7 лет:

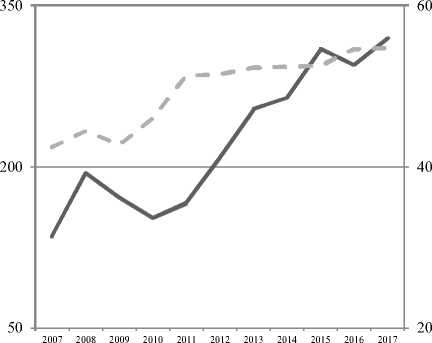
^^^^^^^^ Инвестиции в основной капитал, млрд рублей

Грузооборот транспорта общего пользования, млрд тонн-км

Рис. 3. Динамика изменения инвестиций в основной капитал и грузооборота транспорта общего пользования (по данным 2007–2017 гг.)

Примечание. Составлено авторами.

■ ^л )= XpW             (13)

где g ( t ) – грузооборот транспорта общего пользования, млн т • км;

x ( t )– суммарные взвешенные инвестиции в основной капитал за 7 лет, млн рублей; p > 0.

Учитывая нелинейные эффекты, предположим, что изменение f нелинейно пропорционально его текущему значению ввиду учета взвешенного уровня инвестиций за предшествующие периоды в составе знаменателя базовой функции (13). При этом допустим, что пропорциональность изменения текущей отдачи инвестиций в размерности грузооборота определяется номером периода согласно трендовой логике убывающей отдачи:

ft ) = f ^{( t} ) • ( C 1 + c 2 t )-                (14)

dt

Проведя аналогичные рассуждения для функции f ₁( t ) и применив метод максимального правдоподобия, получим, что соотношение вида (15) описывает зависимость величины грузооборота от инвестиций в основной капитал с учетом фактора времени:

e 0,8440 - 4 • t ² - 0,296 ^ t + 266,45

g ^{( t} ) =

• x - 0,094

Однако околонулевой отрицательный показатель степени p для инвестиций x(t) указывает на противоречие базовой логике ввиду захвата локальной трендовой составляющей грузооборо- та, поскольку тенденции изменения рассматриваемых показателей однонаправлены (рис. 3).

Коэффициент p является положительным, только если в соотношении (14) положить g ’ t )

c 1 = c2 = 0, то есть отношение xpt) является по- стоянным, что означает прямую зависимость грузооборота от величины инвестиций за 7 лет при стационарном влиянии фактора времени. Проведя вычисления по методу максимального правдоподобия, получим уравнение (16):

g ( t ) = e 7,9'5 • x 4 ( t )                      (16)

При этом средняя ошибка аппроксимации составляет 8 = 3,49 %-

Рассмотрим обратную задачу: каким должен быть совокупный объем инвестиций за ретроспективный период времени для достижения определенного уровня грузооборота (g) - Посколь ку g > 0, следовательно решение уравнения (16) существует единственно и имеет вид (17):

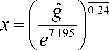
Величина x , необходимая для решения уравнения (17) относительно g ˆ , связана с реальными инвестициями по правилу (3), а значит является линейной комбинацией величин инвестиций за 7 лет, то есть отражает только закон распределения инвестиций по годам.

Для нахождения суммарных инвестиций ( x ) применим подход, основанный на моделировании случайной величины изменения данного показателя относительно исходного значения при допущении нормального закона распределения. Допущение нормальности изменения уровня инвестиций приемлемо исключительно в случае проверки данной гипотезы и основано на необходимости учета инвестиционных циклов и объективного наличия определенной постепенно изменяющейся инвестиционной емкости региональной экономики.

Для иллюстрации суммарных инвестиций ( S ) рассмотрим произвольную гистограмму (см. рис. 4), столбцы которой задают распределение инвестиций за некоторый временной диапазон [ t ₁; t ₂]. При этом величина инвестиции за каждый отдельный год неизвестна.

Вычислим искомую площадь приближенно, линеаризуя функцию инвестиций и применяя решение уравнения (16), а также объем инвестиций за первый год рассматриваемого интервала x ₀. Для этого составим уравнение (18):

h_c ( n ) • z + x ₀ = x , (18)

где неизвестным является параметр z , а величина h_c ( n ) отображает распределение влияния инвестиций согласно весовой функции c ( t ). Для рассматриваемой весовой функции, определяемой отмеченным соотношением, величина h_c ( n ) равна:

n hc (n ) = ^T Z(k -1)^(2 k -1), (19) n k=2

в частности h ( 7 ) =^7-

Введем в рассмотрение функцию ф(t) = z • t + x0, где z - решение уравнения (18)- Функция ф(t) задает линеаризованную зависимость распределения инвестиций по годам рассматриваемого промежутка времени. Тогда площадь фигуры S, а значит и суммарная величина инвестиций, может быть вычислена как определенный интеграл x = j( 2 ф(г)d?, где t1 и t2 - нижняя и верхняя границы рассматриваемого временного промежутка.

Для апробации представленного метода нами спрогнозированы суммарные инвестиции для достижения планируемого грузооборота Ростовской области, равного 60,0 млрд т • км к 2024 году.

Из уравнения (17) получаем x = 391 351,45 млн рублей (сумма «взвешенных» инвестиций по формуле (19) за 2018–2024 гг.). Для составления функции ф ( t ) необходимо найти значение инвестиций x_o за 2018 год. Поскольку на текущий момент времени их величина неизвестна, следовательно ее необходимо спрогнозировать с высокой точностью.

Проверим гипотезу о нормальности распределения показателя «Индекс инвестиций в основ- ной капитал». Согласно критерию согласия Пирсона X2 = 6,76 (Х2набл = 6,76, Х2табл(0,05; 6) = 12,5 Х2набЛ<Х2табЛ(0,05; 6)) данная случайная величина Z распределена по нормальному закону (eN(1,10; 0,18) за период 18 лет – с 2000 по 2017 г. (рис. 5).

Таким образом, численная оценка величины x_o (величина инвестиций за 2018 г.), согласно уравнению (18) с учетом полученного значения x = 391 351,45 находится в диапазоне 295 954,25 <  x_o < 409 561,14.

В результате вычисления соответствующих интегралов от функции j ( t ) при максимальном и минимальном значениях величины x_o получены нижняя и верхняя границы оценок для суммарной величины инвестиций за период 2018–2024 гг., необходимых для достижения целевого грузооборота:

2454268,4 <  x <  2495529,0 .

----------------- 1 ti

Рис. 4. Произвольное распределение инвестиций на промежутке [ t ₁; t ₂]

Примечание. Составлено авторами.

Variable: Индекс инвестиций в основной капитал. Distribution Normal

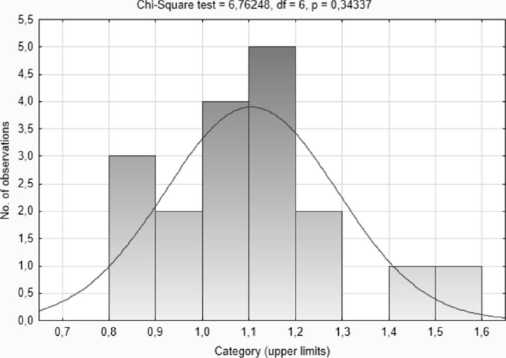
Рис. 5. Распределение Индекса инвестиций в основной капитал по нормальному закону (построено в программном пакете для статистического анализа STATISTICA)

Примечание. Составлено авторами.

Согласно прогнозу Правительства, лежащему в основе Стратегии, суммарные инвестиции за данный период предполагаются на уровне 2 551 800 млн рублей, что на 9,8 % выше прогноза по модели.

Таким образом, отклонение целевого уровня инвестиций от модельной оценки, учитывающей взаимосвязь «Инвестиции – Грузооборот», является дополнительным подтверждением (помимо аналогичной оценки, полученной в ходе анализа связи «Инвестиции – ВРП») рассогласования неявно заложенного допущения об отдаче от инвестиций относительно ретроспективных данных.

Среднедушевые денежные доходы населения Ростовской области находятся практически в прямой зависимости от валового регионального продукта (рис. 6). Таким образом, применение аппроксимирующей линейной регрессионной модели адекватно рассматриваемым данным.

Расчеты показали, что при прогнозируемом целевом уровне ВРП среднедушевые доходы потенциально могут вырасти не более, чем до 46 643 руб. к 2024 г. и до 76 650 руб. к 2030 году. Соответствующие значения, согласно данным Стратегии, существенно выше и составляют 54 028,7 руб. и 99 696,7 руб. соответственно.

Планируемый высокий уровень денежных доходов при целевом сценарии должен быть обеспечен ростом заработной платы, поскольку данные показатели для Ростовской области практически равны. Учитывая отмеченные факты, прогнозируемый рост валового регионального продукта позволит обеспечить значительно меньшую величину денежных доходов и, соответ- ственно, заработной платы при сложившейся его структуре (по доходам). При этом в 2017 г. доля заработной платы в ВРП области составляла 49,8 %. Однако для обеспечения целевых доходов, даже при условии сохранения численности занятого населения на текущем уровне, доля заработной платы в ВРП должна составить 57,8 % к 2024 г. и 61,2 % к 2030 году.

Таким образом, неявно заложенные целевые соотношения заработной платы и экономической базы (ВРП) рассматриваемого региона не реалистичны относительно имеющихся статистических данных, поскольку достижимы лишь при условии существенного снижения инвестиций и/или размера заработной платы и/или размера чистой прибыли. Данный вывод вполне логичен, поскольку за период 2013–2015 гг. (период до завершающего этапа подготовки к ЧМ по футболу) взаимосвязанные и при неизменной структуре экономики условно взаимозаменяемые показатели инвестиций, заработной платы и сальдированного финансового результата условно сопоставимы (табл. 3).

Необходимо отметить, что сценарий увеличения доли заработной платы в ВРП теоретически реализуем. Однако его достижение при сохранении текущей мотивации участников экономической системы, стремящихся к максимизации прибыли с сохранением как минимум текущей рентабельности операционной деятельности, возможно исключительно в случае увеличения отдачи от инвестиций. В то же время предшествующий анализ, напротив, указывает на неявное допущение снижения отдачи в прогнозном периоде.

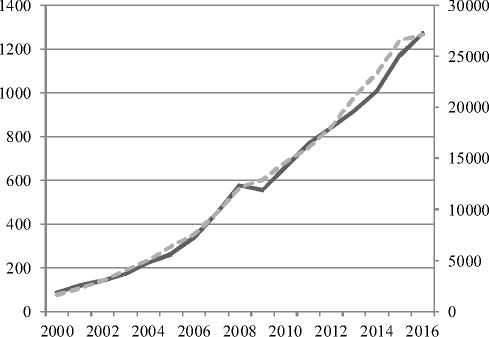
-     ВРП, млрд рублей

Рис. 6. Динамика изменения валового регионального продукта и среднедушевых денежных доходов населения (по данным 2000–2017 гг.)

Среднедушевые денежные доходы населения, рублей

Примечание. Составлено авторами.

Заключение

По результатам представленного исследования применительно к его объекту – Стратегии социально-экономического развития Ростовской области – представляется возможным сформулировать следующие выводы:

• 1)    модельный аудит взаимосвязей «Инвестиции – ВРП» и «Грузооборот – Инвестиции» указывает на системно заложенную неявную предпосылку уменьшения отдачи на вложенный капитал. Более того, снижение отдачи от инвестиций противоречит заявленной цели и миссии Стратегии, предполагающим, напротив, рост производительности и интенсификацию экономики региона;

• 2)    модельный аудит взаимосвязи «Среднедушевые доходы – ВРП» указывает на существенное увеличение доли заработной платы в ВРП даже при консервативной оценке сохранения численности занятого населения, что достижимо прежде всего при условии сокращения инвестиций при их неизменной отдаче либо их роста в случае соответствующего прироста рентабельности вложений;

• 3)    в целом сопоставление результатов модельного аудита с точки зрения инвестиционных эффектов и эффектов заработной платы также позволяет сделать вывод о системном несоответствии уровня заработной платы в ВРП и понижении отдачи на вложенный капитал.

Применительно к подходам проведения модельного аудита целесообразно выделить следующие этапы, реализованные в настоящем исследовании и необходимые для моделирования и верификации количественных параметров стратегического документа:

• 1.    Формирование формально-логической структуры факторов динамики развития терри-

• тории и постановка соответствующей гипотезы о формах зависимостей между ключевыми факторами экономического роста.

• 2.    Спецификация и построение экономикоматематических моделей на базе выдвигаемых гипотез и их верификация.

• 3.    Проведение анализа временных рядов показателей на предмет допустимости применения регрессионных моделей либо нелинейных форм зависимости, являющихся решениями дифференциальных уравнений, квантифицируемых через метод наибольшего правдоподобия. В частности, выбор дифференциальной модели обусловлен наличием нелинейной завимости целевых экономических показателей (ВРП, грузооборот транспорта общего пользования) от неравномерно распределенных во времени эффектов инвестиций в основной капитал.

На наш взгляд, перечень целевых индикаторов развития региона следует расширить показателями эффективности регионального управления. В частности, включить в качестве индикатора эффективности региональной политики «объем налоговых и неналоговых доходов консолидированного бюджета субъекта России» [Перечень показателей ... , 2017], который выступает источником инвестиций в экономику региона.

Как показывают исследования отечественных экономистов, инвестиции в основной капитал и налоговые доходы регионального бюджета взаимосвязаны [Кабанов, Жильников, Заб-лоцкая, 2018]. С помощью разработанного нами инструментального подхода представляется возможным определить данную зависимость применительно к Ростовской области для оценки финансовых инструментов, находящихся в распоряжении региональных государственных органов власти.

Таблица 3

Сопоставление целевого прогноза Правительства Ростовской области и прогноза по предложенной модели

Год	Среднемесячная начисленная заработная плата, тыс. руб.	Инвестиции в основной капитал, млрд руб.	Инвестиции за счет бюджетных источников, млрд руб.	Сальдированный финансовый результат, млн руб.
2013	21,9	253,6	38,0	47,2
2014	23,8	264,2	27,7	5,7
2015	25,0	309,4	44,6	32,9
2016	26,7	294,5	70,7	85,8
2017	28,5	319,3	91,3	56,6

Примечание. Составлено авторами.

В настоящем исследовании авторы не стремились к детальному описанию факторов регионального развития и комплексному моделированию экономической динамики. Данное направление планируется развивать в дальнейшем. Задачей текущего этапа являлось получение обобщенных и простых моделей динамики конкретного региона и проверка с помощью разработанного инструментария согласованности и реализуемости прогнозов, изложенных в стратегических документах. Следующим шагом в построении комплексной региональной модели станет системная доработка уравнений с включением дополнительных социально-экономических факторов, уточнение коэффициентов моделей, представляющих собой обобщенные сложные зависимости.