Модификация алгоритма Узнадзе в аспекте кратковременной и долговременной памяти робота

В работах [1, 2] предложены математические определения эмоции робота, воспитания и уровней воспитания, относительной невосприимчивости робота к воспитанию, основанные на гипотезе грузинского психолога Д.Н. Узнадзе [3–5], с учетом коэффициентов кратковременной памяти робота.

Определение 1 . Воспитанием робота R(t ) (воспитание робота во время действия эмоции) назовем функцию вида

R , ( t ) = r , (t ) + e , ( t ) R , _ 1 (t, ) ,        (1)

где t - текущее время, t >  t, , 0 <  ^ ( t ) < 1. Текущее время удовлетворяет соотношению t = t + t_i , где t - текущее время действия настоящей эмоции от начала ее проявления, t – общее время действия всех предыдущих эмоций, R _; ( t _;) - воспитание, полученное роботом за время t .

В алгоритме Узнадзе в работе [1] введено допущение о равенстве и постоянстве

коэффициентов кратковременной памяти θ , соответствующих конечному моменту времени каждой эмоции, предложены определения уровня воспитания робота k и невосприимчивости робота к обучению (воспитанию) s_k .

Отметим, что алгоритм многоуровневого воспитания робота, описанный в статье [1], не учитывает долговременную память робота.

Новая многоуровневая модель воспитания робота

Предложим новую многоуровневую модель воспитания робота, которая учитывает кратковременную и долговременную память робота.

Воспитание робота на конкретном уровне k ограничено пределом воспитания робота на k -ом воспитательном уровне U ^{[ k ]} . Переход на новый уровень воспитания происходит для "активизации" воспитания (обучения) робота. И так до тех пор, пока воспитание робота не достигнет «цели» воспитания G (рис. 1).

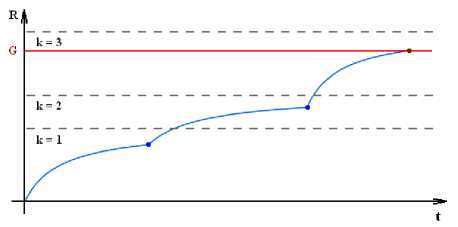
Рис. 1. Решение проблемы " пресыщения " воспитания робота

Следовательно, для равномерно забывчивого робота, который на каждом воспитательном уровне к обладает только равноценными положительными эмоциями, справедливы соотношения

R j ^Ч= £ И^] ) m q^{1 к ]} , m = 0

R j^к ]

= q ^{[ к ]}

1 - ( #^{[ к ]} ) ^j

1 - 0[к]   .

Воспитание робота вычисляется по формуле (1) и зависит от начальных параметров, в т.ч. эмоций роботов. Легко видеть, что воспитание робота не зависит от цели воспитания G. В частном случае допустимо, что величина G будет меньше предела воспитания робота на 1-м воспитательном уровне U[1]. В общем случае это условие может не выпол- няться.

Смена набора эталонных эмоций (установок) дает возможность изменить начальные параметры формулы (1), и следовательно, определяет предел воспитания робота U ^{[ k ]} на воспитательном уровне с порядковым номером к .

Определение 2. Локальным воспитанием робота на уровне k назовем воспитание [ к ]

робота R j ( т ) , полученное на воспитательном уровне к без учета воспитания на предыдущих уровнях. j - номер воспитательного такта на уровне к.

Не нарушая общности, представим воспитательный процесс (1) на уровне к следующим образом:

; r о% )=r к](т)R^t) = r।к](т) + •< к](/)RS, j > 0

jj

[к где Rj (т) - локальное воспитание на уровне к при такте i, r.к] (т) - элементарное воспитание на уровне к для такта i, 0^к] (т) - ко- эффициент кратковременной памяти на уровне к для такта i.

Будем считать, что робот равномерно забывчив, т.е. справедлива цепочка равенств 0[к] = ^0к] (т) = ... = 0[„к] (т) = ... Пусть робот обладает только равноценными положитель- ными эмоциями на каждом воспитательном уровне к: q[к ] = r0[ к ] = .. = r^к ] = ...

Таким образом, воспитание робота Rj непрерывно и ограниченно, т.е. на языке теории эмоциональных роботов воспитание робота имеет пресыщение. Из соотношения (4) получаем предел воспитания робота на воспитательном уровне k при бесконечном уве- личении количества тактов j:

U [ к ] = l™ R j" ] =          .

j^        1 - £[ ^{к ]}

При переходе с одного уровня воспитания робота на другой наряду с коэффициентом кратковременной памяти 0^{[ к ]} будем учитывать коэффициент долговременной памяти 0 ,^{[ к ]} . Будем предполагать, что 0_t ^{[ к ]} влияет на воспитание робота R ^[ . ^{к - 1]} , которое им было ik - 1

получено на всех предыдущих воспитательных уровнях, где i*k-1 - номер последнего так- та уровня k-1, на котором происходит переход на уровень k.

Таким образом, будем считать, что воспитание на каждом уровне и на каждом такте будет удовлетворять равенствам

R;"(' )=Rj'(')                        «й rJ к] (t )=r [к] (t)+0‘] (t)r,f-1], к > 1, ik-1

где R i^{к ]} ( т ) - воспитание робота на уровне к [ к ]

при такте i , R j ( т ) - локальное воспитание на уровне к при такте j , 0^^{к ]} ( t ) - коэффициент долговременной памяти на уровне k для такта i , 0 <  0 i^{к ]} ( t ) <  1.

Взаимосвязь между i , номером воспитательного такта, и j , номером воспитательного такта на уровне k , можно представить следующей системой равенств:

i = j, к = 1

1-    -.-*                         (7)

li = J + 1к-1, к > 1

Теорема 1. Если все коэффициенты долговременной памяти 0- k ^] постоянны на каждом воспитательном уровне, то воспитание для каждого воспитательного уровня имеет предел.

Доказательство. Так как по условию теоремы справедлива цепочка  равенств

0^{[ k ]} = 0 0 ^{k ]} ( t ) = ... = 0 0^{k ]} ( t ) = ... ,               то

C ^{[ k ]} = 0^{[ k ]} R ^[ . ^{k - 1]} является константой для ка- i k - 1

ждого уровня k.

Следовательно, справедлива цепочка равенств

R [k ] (t) = R j] (t)+ 0k ] (t)R [*k-1] = ik-1

_ p ^[ k ^]          [ k ] p[k - 1] _ p^{[ k ]}          [ k ]

= R j ( t ) + 0   R, «    = R j ( t ) + C .

Переходя в равенстве (8) к пределу при j ^ те и учитывая справедливость формулы q^{[ k} ]

(5), получим lim R ^{[ k ]} =----- — + C^{[k ]} .

j ^ i     1 - 0 L ^{k ]}

Таким образом, теорема доказана.

Введем критерий перехода воспитательного процесса с одного уровня на другой. Будем считать, что точка перехода с воспитательного уровня k на уровень k +1 достигается, когда изменение воспитания робота на воспитательном уровне k становится меньше некоторой величины 3 (рис. 2):

R [ ^k ] -R^lk ]

tg a = R i---- R^ = R ^{[ k ]} - R ^{[ k} ] <  3 .   (9)

i - i + 1

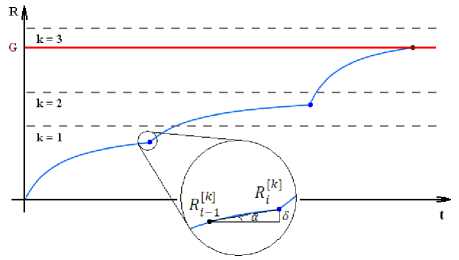
Рис. 2. Визуализация критерия воспитательного процесса с одного уровня на другой

Причем величина 3 не зависит от воспитательного уровня k .

Докажем следующую теорему.

Теорема 2 . При условиях теоремы 1 на каждом воспитательном уровне k существует такой такт i , для которого справедливо неравенство R ^{[ k ]} - R ^{[ k ]} | <  3 .

Доказательство. Так как ряд R ^{[ k ]} сходится, то верно следующее утверждение:

V 3 , Я n g N , V i >  n : R [ ^{k ]} - R [ ^k ]¹ 1 <  3 .

Таким образом, теорема доказана.

На основе теоремы 2 можно сделать вывод, что на любом воспитательном уровне k найдется номер такта i , при котором произойдет переход на следующий воспитательный уровень и критерий, задаваемый формулой (9), выполняется для любого воспитательного уровня k . В свою очередь это означает, что воспитание робота при равноценных положительных эмоциях, постоянном коэффициенте долговременной и кратковременной памяти робота для каждого воспитательного уровня не ограничено сверху, а значит, может достигнуть любую "цель" воспитания G .

Исходя из вышеизложенного, можно предложить следующий алгоритм воспитательного процесса с учетом смены эталонных эмоций (установок) робота и коэффициентов кратковременной и долговременной памяти робота.

Шаг 1. Задаем эталонную эмоцию M ^[1] , i = 0 , j = 0 , k = 1 .

Шаг 2. Вычисляем элементарное воспитание Г ^{[ k ]} = J M ^{[ k ]} dt .

Шаг 3. Вычисляем воспитание робота R i "( t ) :

' R 0 ^{k ]} ( t ) = Л)

R [" ( t ) = r'^k’ ( r ) +0 k ^] ( t ) R ^, j >  0 jj

R‘ⁿ(> ) = R j ^1] ( t )                           ’

R^{1 k ]} ( t ) = Ri k ^] ( t ) + 0 k ^] ( t ) R 4 ^{- 1]} , k >  1

i k - 1

где 3 [. ^{k ]} ( t ) и 0 i^{k ]} ( t ) - кратковременная память и долговременная память на уровне k соответственно.

Шаг 4. Если R [ ^k ] ( t ) = G , то КОНЕЦ, в противном случае переходим к Шагу 5.

Шаг 5. Если выполняется критерий перехода     на     следующий     уровень

|R i^{k ]} - R ^j < 3 , то С = i , j = 0 , к = k + 1 . Переходим к Шагу 6.

Шаг 6 . j = j + 1 , i = j + i *__t и перейти к шагу 2.

Заключение

Таким образом, в настоящей статье приведены математические модели коэффициентов долговременной памяти робота и предложен алгоритм воспитательного процесса с учетом смены эталонных эмоций (установок) робота и коэффициентов кратковременной и долговременной памяти робота. В статье также описаны основные математические свойства сходимости, присущие воспитательному процессу роботов, и доказано, что любая вос- питательная цель, поставленная перед роботом, является достижимой.