Модификация метода Фехнера для повышения устойчивости анализа данных

Одним из наиболее востребованных на практике направлений статистических исследований является изучение зависимостей между различными варьирующимися признаками. Решение данной задачи может предшествовать построению математической модели рассматриваемого явления или служить обоснованием для реализации каких-либо методик обработки данных, интерпретации получаемых результатов, а также для поиска причинно-следственных связей между процессами. Не случайно спектр способов практического использования корреляционного анализа достаточно широк.

Для оценки линейной зависимости в условиях классических параметрических распределений количественных показателей, близких к нормальному, используют традиционный коэффициент корреляции Пирсона. Для случаев нелинейного влияния факторов применяют методы регрессионного анализа [1]. Если количество изучаемых факторов велико, то обращаются к средствам факторного анализа [2]. В непараметрических ситуациях, когда нарушены условия нормального распределения характеристик или при сложности обоснования данного факта [3; 4], чаще исследуют зависимость между признаками критерием ранговой корреляции Спирмена или при помощи коэффициента корреляции Кендалла [5; 6]. Изучение дихотомических совокупностей производят при помощи коэффициентов ассоциации Ф , тетрахорических коэффициентов, углового преобразования Фишера и т. д. [7].

Среди перечисленных способов исследования корреляционной связи относительной простотой и универсальностью выделяется метод Фехне-ра, позволяющий установить наличие и направление зависимости между наборами данных или ее отсутствие [8]. Этот метод является непараметрическим, может применяться в условиях малой выборки, что делает его привлекательным. В данной работе предлагается способ повышения устойчивости данной методики по отношению к наличию некорректных наблюдений, снижающих качество выборки.

Модификация метода Фехнера

Рассмотрим подробнее метод Фехнера. Пусть даны два массива данных X = { x 1 , x ₂, .„, x _n}, x i e R и Y = {y ₁, y ₂, .„, y _n}, y i e R объёмом n . Для каждой пары наблюдений { x i , y i } определяется, совпадает ли знак разности между текущим элементом и средним арифметическим данного массива. Подсчитывается количество таких совпадений v и несовпадений w:

v = ^i , при sign ( x_f - x ) = sign ( y_t - y )                 (1)

I = 1

и w = ^i, при sign (xi - x )# sign (yi - y ),                (2)

i = 1

где x и y — средние значения соответствующих массивов X и Y . Причем нулевые отклонения наблюдений от среднего считаются положительными.

Далее вычисляется коэффициент Фехнера ( K ф ):

v - w _ v - w v + w   n

Величина коэффициента Фехнера может принимать значения от -1 до 1 и интерпретация данного показателя аналогична классическому коэффициенту корреляции. Близость к нулю говорит об отсутствии линейной зависимости массивов Хи Y , что происходит при примерно одинаковом количестве v и w. Наличие же корреляционной связи определяется в виде прямой зависимости при приближении K ф к 1 в случае значительного преобладания v или обратной зависимости при стремлении K ф к -1 в случае роста w .

Преимуществами данного метода является простота вычислений и программной реализации, а также независимость от закона распределения изучаемых массивов данных.

Ферстер и Ренц в работе [7] показывают, что величина коэффициента Фехнера вполне сопоставима с коэффициентом корреляции Пирсона ( r ). Однако данное утверждение подтверждается другими исследователями лишь при сильной тесноте связи (| К ф | и | r | е[0,8; 1]) [9]. Авторами [10] было построено уравнение регрессии между К_ф и r при доверительной вероятности 0,95 и интервалом существования А К ф = ±0,0702:

К _ф = 1,237 r - 0,438.

В работе [10] предлагается модифицированный индекс Фехнера, рассчитываемый по формуле:

_ *        „ „ v — w _

К, = ±0,949. -----± 0,051 , ф \v + w где знаки слагаемых положительны при v > w и отрицательны при v < w.

Без сомнения, приведенные выше вариации метода Фехнера носят частный характер и были получены эмпирическим путем на основе пусть и многочисленных, но все же конкретных наборов данных.

Вместе с тем можно предложить скорректировать методику определения знаков отклонений в выражениях (1) и (2), заменив среднее арифметическое на медиану.

Соотношения (1) и (2) в этом случае примут вид:

^v = ^^i , при sign ( X, ^- x мед ) = sign ( У, - y мед )                   (4)

i = 1

и w = ^ I, при sign (x, - x мед ) * sign (У, - У мед ) ,                 (5)

i = 1

где x _мед и y _мед — медианы массивов X и Y .

Действительно, в случае если единицы исследуемой совокупности расположены близко к нормальному распределению, то медиана незначительно отличается от среднего арифметического. Если же в наблюдаемых значениях прослеживается асимметричность или в выборке присутствуют

«выбросы» [13], то медиана нивелирует влияние таких данных. В отличие от среднего арифметического медиана является несмещенной оценкой [11; 12].

Приведем пример, иллюстрирующий большую устойчивость (робастность) метода Фехнера при использовании медианы (табл. 1 и 2).

Таблица 1

Пример реализации метода Фехнера без «выброса»

№	X	Y	Знак отклонения				Совпадения зна ков
			X		Y
			xi - x	X- - X i мед	yi - y	y i - y мед	среднее	медиана
1	951	83	—	+	+	+	не совп.	совп.
2	874	76	—	—	—	—	совп.	совп.
3	957	84	+	+	+	+	совп.	совп.
4	1084	89	+	+	+	+	совп.	совп.
5	903	79	—	—	—	—	совп.	совп.

Для данных массивов X и Y найдем средние величины:

х = 953,8 ; у = 82,2 ; х мед = 951 и у мед = 83 .

В таблице 1 приведены знаки разности наблюдений и средних, а также совпадения и несовпадения этих знаков.

В данном случае отличие между средними и медианами незначительно. Определим коэффициенты Фехнера для обоих вариантов (3):

К ф(срецнее)    ^{0,6; К} ф(мецuаиа)    ^1.

Коэффициент корреляции Пирсона здесь составил r = 0,966.

Для полноты примера оценим статистическую значимость найденной корреляционной связи

Т , = К,, набл        ф (среднее)

\'

к

ф (среднее)

0,6 , ^8     ~ 2,12.

тг-от7

Табличное значение критерия Стьюдента для вероятности 0,1 составляет t _табл = 1,86.

Так как T _набл >  t _табл, то гипотеза о нулевой корреляции отвергается. Полученный К ф (среднее) статистически значим.

Оценим значимость коэффициента Фехнера, рассчитанного по медиа- не.

= 1

- 2

ф (медиана)

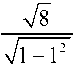
> Ю .

т , = К

^ набл ф (медиана)

T _набл >  t табл , следовательно К ф ( _медиан а) также статистически значим.

Теперь придадим исходным данным асимметричность (табл. 2), увеличив одно из значений множества X (в 4-й строке).

Таблица 2

Пример реализации метода Фехнера с «выбросом»

№	X	Y	Знак отклонения				Совпадения зна ков
			X		Y
			X i - X	X- - X i      мед	У , - У	У , - У мед	среднее	медиана
1	951	83	—	+	+	+	не совп.	совп.
2	874	76	—	—	—	—	совп.	совп.
3	957	84	—	+	+	+	не совп.	совп.
4	1123	89	+	+	+	+	совп.	совп.
5	903	79	—	—	—	—	совп.	совп.

Увеличение разброса наблюдений привело к изменению среднего арифметического, в то время как значение медианы осталось прежним:

X = 961,6 ; У = 82,2 ; x мед = 951 и у мед = 83 .

Коэффициент Фехнера, основанный на среднем арифметическом, также изменился:

К„ =0 2-        =1

ф (среднее) ^о^^{2 ;}     ф (медиана)

Коэффициент корреляции Пирсона в этом случае составил r = 0,944.

Безусловно, приведенный пример не является репрезентативным, он лишь демонстрирует особенности использования медианы вместо среднего арифметического в случае асимметричности данных.

Для оценки значимости полученного результата мы использовали t -критерий Стьюдента, в основе которого также лежит сопоставление различий наблюдений и их среднего арифметического. В [15] показано, что параметрические критерии достаточно устойчивы к отклонениям выборочных законов распределения от нормального при проверке предположений о равенстве математических ожиданий. Анализ мощности и устойчивости таких критериев для различных ситуаций приведен в работах [16-18].

Основываясь на утверждении Б. Ю. Лемешко [15-21] о том, что критерий Стьюдента с ростом объемов выборок становится устойчивым к на -личию асимметрии в законе распределения и не приводит к серьезным ошибкам, сопоставим степень восприимчивости медианного метода Фех-нера по сравнению с классическим.

Для анализа робастности были выбраны данные, полученные на основе многолетних наблюдений за результатами разновозрастных спортсменов Иркутской области в некоторых циклических видах спорта. В работе [13] была предпринята попытка построить зависимость уровня работоспособности или показываемых результатов от возраста. Используя ту же математическую модель и решая обратную задачу оценки возраста по имеющемуся спортивному результату, придадим исходным данным некоторый ограниченный псевдослучайный разброс. Средний предполагаемый результат составил 12 минут, что соответствует времени преодоления дистанции 3 км человеком, не занимающимся легкой атлетикой профессионально, в среднем возрасте — 30 лет. Диапазон разброса выбран ±1,5 минуты. Генерация разброса осуществлялась по методике Макото Мацумото алгоритмом «Вихрь Мерсенна» [22], применяемом в реализации функции выбора случайного числа MS Excel. Рассматривались выборки объемом 10, 50 и 100 наблюдений. Было проведено 1000 испытаний. При этом анализировались две выборки: полученная на основе описанной выше модели и с «выбросом» – некоторым искусственно завышенным показателем времени. Завышение в выборке объема 10 составило 1 наблюдение (10%), в выборках объема 50 и 100 — по 2 намеренно высоких данных (4 и 2% соответственно). Величина завышения — случайное число в пределах 90-100%. Полученные усредненные результаты приведены в таблице 3.

Таблица 3

Усредненные результаты реализации

1000 повторений метода Фехнера (классического и с «выбросом»)

Объем наблюдений	10	50	100
Коэф. Фехнера классический	0,314	0,392	0,314
Коэф. Фехнера медианный	0,294	0,391	0,314
Коэф. Фехнера классический с выбросом	-0,045	0,357	0,296
Коэф. Фехнера медианный с выбросом	0,284	0,394	0,317
Коэф. корреляции	0,281	0,297	0,276
Коэф. корреляции с выбросом	0,288	0,279	0,256

Из таблицы 3 видно, как меняется значение классического коэффициента Фехнера при наличии асимметрии данных. В малой выборке его величина изменилась с 0,314 до -0,045, в то время как медианный коэффициент Фехнера остался достаточно стабильным. Не так наглядна эта тенденция при росте объема выборки, тем не менее она видна. В совокупности в 100 единиц наличие 2% выбросов привело к изменению традиционного показателя Фехнера с 0,314 до 0,296, а медианный в тех же условиях изменился с 0,314 до 0,317. Для сопоставления в таблице также приведены усредненные показатели корреляции Пирсона для всех выборок.

На каждом шаге исследования проводилась оценка значимости получаемых результатов критерием Стьюдента. Критерий Стьюдента реализовывался с вероятностью получения ошибки первого рода p = 0,1. Усредненный анализ значимости результатов из табл. 3 приведен в следующей таблице:

Таблица 4

Усредненные результаты анализа значимости

1000 повторений метода Фехнера (классического и с «выбросом»)

Объем наблюдений	10	50	100
Средняя значимость классического коэф. Фехнера	0,580	0,388	0,309
% значимых наблюдений	17,6	74,3	92,3
Средняя значимость медианного коэф. Фехнера	0,569	0,349	0,284
% значимых наблюдений	19,3	74,2	91,2
Средняя значимость классического коэф. Фехнера с «выбросом»	0,632	0,312	0,261
% значимых наблюдений с «выбросом»	9	25	35,6
Средняя значимость классического коэф. Фехнера с «выбросом»	0,578	0,267	0,233
% значимых наблюдений с «выбросом»	15,6	67,3	88,7

Таблица 4 показывает оценку значимости модели Фехнера для рассматриваемой задачи моделирования работоспособности спортсменов. Результаты исследования значимости классического метода Фехнера не сильно отличаются от медианного при всех трех объемах выборки. Однако наличие «выбросов» существенно снизило процент наблюдений, которые критерием Стьюдента признавались значимыми. Медианный критерий Фехнера в аналогичных условиях демонстрирует гораздо бо́льшую робастность относительно выбросов по сравнению с традиционным критерием.

Заключение

Проведенное исследование показало возможность повысить устойчивость критерия Фехнера к наличию в выборочных данных незначительного количества некорректных наблюдений за счет использования медианы вместо среднего арифметического. Предложенная модификация классического метода Фехнера апробирована на модели зависимости возраста человека от показываемых им спортивных результатов. Реализация данной модели в количестве 1000 повторений с псевдослучайным разбросом исходных данных, а также внесение в эти данные небольшого числа искусственно завышенных значений позволяет сделать следующие выводы:

• 1.    Модификация классического метода Фехнера оценивания зависимости между наборами выборочных наблюдений путем замены среднего арифметического медианой не приводит к усложнению процедуры его реализации.

• 2.    Рост объема наблюдений способствует выявлению корреляционной зависимости или независимости как при использовании классического, так и медианного критерия.

• 3.    Наличие в выборке даже незначительного количества «выбросов» способно существенно снизить устойчивость классического метода Фех-нера. Медианный метод при этом остается достаточно невосприимчивым к асимметрии в наблюдениях.