Mollifications of contact mappings of Engel group

Mollification or convolution with a smooth kernel is one of the main tools of analysis that allow us to transfer results from spaces of smooth functions to more general function spaces. However, for contact mappings, that is mappings that preserve a fixed distribution in the tangent bundle, mollifications lead to an undesirable effect: the mollified mapping is not contact anymore. In [1, 2] it is shown that at least for mappings between two-step Carnot groups we can give estimates on the failure of the mollified mapping to be contact sufficient to prove convergence of horizontal differential forms

(f ^e ) * _Ш ^ f * _Ш

(1.1)

as E ^ 0 in L ^v , here f # is a pull-back of the form with the Pansu differential d of the contact mapping f , ν is the Hausdorff dimension of Carnot group. The formula (1.1) in turn allows to obtain a crucial fact of quasiconformal analysis

df *ш = f *du

(1.2)

in distributional sense. In the theory of mappings with bounded distortion developed by Yu. G. Reshetnyak [3, 4] the commutativity of outer differential and superposition allows to prove that the superposition u = v о f of n -harmonic function v on R ⁿ with the bounded distortion mapping f is a weak solution of the quasilinear elliptic equation div A (x, V u) = 0 .

For 2-step Carnot groups in [1, 2] a weaker statement is proved: if dw = 0 in weak sense, then df # w = 0 . In full the formula (1.2) is proved in [5] for mappings of 2-step Carnot groups and in the recent preprint [6] for mappings of Carnot groups of arbitrary step. The proof of (1.2) in [5] does not rely on the convergence of mollifiers (1.1) but relies essentially on 2-step structure of the group. In [6] the formula (1.2) is derived from (1.1).

In this paper we obtain for a contact mapping f on Engel group E (the simplest example of 3-step Carnot group) estimates on convergence (or sometimes divergence) of components of the “Jacobi matrix” of the mollified mapping f ^ε . However, in order to obtain meaningful estimates we should compute this matrix not in the Euclidean basis but in the graded basis of left invariant vector fields. Precisely, if X 1 , . . . , X 4 is a graded basis of the algebra of leftinvariant vector fields of Engel group, we are interested in the behavior as e ^ 0 of the coefficients a _i ^ε _j in the decomposition

X i f ^e = dfX } = £ a j X j , i = 1,..., 4.

j =1

If we introduce the dual basis of 1-forms £ i ,... ,£ 4 such that £ i { X j } = d j , i, j = 1,...,4 , the coefficients are a j = £ j { X i f ^e ) . By a form of the weight l we mean 1-form dual to the vector field of the degree l (and thus having the homogeneous degree — l ). The main result of the paper is the following

Theorem 1.1. Let Q, Q ‘ C E, f : Q ^ Q ‘ be weakly contact of class W^^Q). If X is a left-invariant vector field of the degree k, £ is a left-invariant 1-form of the weight l, p ^ l, then on every compact K C Q we have

'O(El-k), l>k, l = k, l < k,

£{Xf^ = Uff {X» + o(1), .°(—), as e ^ 0 in Lp/l(K).

Section 3 of this paper is dedicated to the proof of the theorem in Engel case. For Engel group the result is new and may have independent interest, it also serves as an alternative way to prove (1.1) and (1.2). The analogue of Theorem 1.1 for 2-step groups follows from Lemma 2.1 and Lemma 3.3 in [2]. To prove Theorem 1.1 on Engel group we modify the approach of [2] to obtain finer estimates on divergence of components of the mollified mapping.

2.    Carnot Groups

Recall that a stratified graded nilpotent group or a Carnot group (see e. g. [7–9]) is a connected simply connected Lie group G such that its algebra of left-invariant vector fields g decomposes into the direct sum g = V i ® V 2 ® • • • ® V m of vector spaces V k satisfying [V i , V k ] = V k+i , k = 1,..., M — 1 , and [V i , V m ] = { 0 } . Left-invariant vector field L E g is the field of the degree k if L E V k . The subspace V i = H G is a horizontal space of g , its elements are the horizontal vector fields .

Elements g E G in some “privileged” coordinate system may be identified with elements (x 1 ,..., x _M ) E R dim V ¹ x ••• x R dim V M = R N in a way that dilations 5 _X : R N ^ R N , A > 0 , defined by 5 _x (x i , X 2 ,..., x m ) = (Ax i , A ² X 2 ,..., A M x m ) are group automorphisms.

The homogeneous norm on G is a function || • || : G ^ R such that

• 1)    | 0 | = 0 , I g l > 0 , when g = 0 ;

• 2)    p_Ag | = A l g l for all A >  0 , g E G ;

• 3)    there is Q ^ 1 such that | gh | C Q( | g | + II h | ) for all g, h E G .

The homogeneous norm generates left-invariant homogeneous quasimetric d(g, h) = ||h ^-1 g | . In constract to metric it satisfies only the generalized triangle inequality

d(gi,g3) C Q(d(gi,g2)+ d(g2,93)),   gi,g2,g3 E G, where Q ^ 1 is a constant from the definition of the homogeneous norm.

The ball in this quasimetric with the centre g E G and the radius r denote by B _r (g) . The topology given by d coincides with the Euclidean topology of R ^N . The Lebesgue measure dx on R N is the bi-invariant Haar measure on G and d(5 _x x) = A ^v dx , where v = ^ j=i j dim V j is the homogeneous dimension of the group.

Let Q C G be open. The space Lp(Q), p ^ 1, consists of measurable functions u : Q ^ R integrable in the p-th power. The norm on Lp (Q) is defined by llullp,Q =

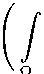
When Q = G , we write | u | _p = ||u | _p, G .

Let left invariant vector fields X 1 , . . . , X _n be the basis of the horizontal space HG . The

Sobolev space W ^i,p (Q) , p ^ 1 , is a space of functions u E L ^p (Q) that have distributional

derivatives X j u E L ^p (Q) along the vector fields X j , j = 1,..., n , that is such functions g j

that

j gj (x)^(x) dx

Ω

j u(x)Xjy(x) dx,

Ω

j = 1,...^,n,

for all ^ E C 0 ” (Q) . The norm on W ^i,p is ||u | W ^i,p (Q) | = | u | p,Q + || |V _H u | || _{p Q} , where V H u = (X i u,... ,X _n u) . We say that u E L p _oc (Q) and v E WO’cCQ) , when u E L p (K ) and v E W ^i,p (K ) for each compact K C Q . A mapping f : Q ^ G f = (f i ,..., J n ) is in class W ^{i ,p} (Q) or W _l ⁱ _o ^, _c ^p (Q) if all its components f j are in the corresponding class.

A mapping f : Q ^ G of class W^^Q) is (weakly ) contact if X j f(x) E H f (_x) G , j = 1,...,n , for a. e. x E Q . The formal horizontal differential d H f (x) : H _x G ^ H f (_x) G of a contact mapping f is a linear mapping such that d H f (x) ( X j ) = X j f (x) . It is proved in [10, 11] that the horizontal differential extends to the contact homomorphism of Lie algebras df (x) : T _x G ^ T f (_x) G that we call the formal Pansu differential ( P -differential) of f at x .

The convolution of measurable functions u, v on Carnot group G is defined as u * v

^{( x )}=/

G

u(y)v(y ix) dy

u(xy-i)v(y) dy,

G

x E G,

if the integral converges.

Lemma 2.1 (Convolution Properties [8]) . 1. Let p,q E [1, + ^ ], u E L ^p (G), v E L ^q (G). Then u * v E L ^r (G), where p + q = Г + 1, and the following Young inequality holds

||u * ^{v |} r ^C H u H p ^{| v |} q .

• 2.    If L is a left invariant vector field on G, u, v are smooth compactly supported functions, then

L(u * v) = u * (Lv),   (Lu) * v = u * (Lv), where L is the right-invariant vector field agreeing with L at the origin.

For у : G ^ R and e >  0 define

W(x) = eVV ° < ;x),  x € G, where v is the homogeneous dimension of G. If у € L1(G), then G v(x) dx = G y(x) dx.

Lemma 2.2. For every у € C 0 ” (G), left-invariant field L of the degree k and right-invariant field L such that L(0) = L(0) we have

¹         T     ¹ TA

^Ly e — e k ^{( Ly )} e ,   LV e — e k ^{( Ly ) e} •

<1 Since dilation 6 a is an automorphism of G , that is 6 a ( x • y) = 6 a x • 6 а У , for the left translation l _x (y) = x • y we have 5 \ ° l x = l g _x x ° 5 \ . If L(0) € V k (0) , then D5 \ L(0) = A ^k L(0) . Therefore, for left-invariant L € V k

D^ ( L(x) ) = D5 _X ° Dl x ( L(0) ) = Dl _{5 x} x ° Dd _A ( L(0) ) = A ^k L^x).

Thus,

^L v e ^{( x )} = e V ^{L (}v ° ⁵ i/e ^{)( x )} = e V • e k ( L^to^^x) = e k ^(L ^ ^{) e (x)} .

Obviously, the same argument holds for the right translation r _x (y) = y • x . >

Lemma 2.3 (Properties of Mollifications [8]) . Let у € C q°( G ) and G y(x) dx = a. Then

• 1.    If u € L₁¹_oc(G) then u * у, ^ au a.e. as e ^ 0.

• 2.    If u € L^p(G), p € [1, +ro), then ||u * v — au|_p^ 0 as e ^ 0.

• 3.    If u is bounded on G and is continuous on open set Q C G then u * y_e^ au uniformly on compact subsets of Q as e ^ 0.

3.    Mollifications on Engel Group

Engel group E is a 4-dimensional 3-step Carnot group i. e. E = (R ⁴ , • ) , and g (E) = V i Ф V 2 Ф V 3 , dim V i = 2 , dim V 2 = dim V 3 = 1 . Such a group is unique up to an isomorphism.

For convenience we use coordinate system (x, y, z, t) such that the group operation has the form

^{( x},y,z,^{t )( x} ‘ ,y ‘ ,^z ‘ ,t ‘

)=

x + x, y + y ,z + z ‘ + xy ‘ , t + t ‘ + xz +

x ² y ^′ "Г"

.

Thus, the dilation is

5A(x, y, z, t) = (Ax, Ay, A2z, A31), algebra of left-invariant vector fields is spanned by the graded basis

X = dx,  Y = dy + xdz + 2x2 dt,  Z = [X,Y] = dz + xdt,  T = [x,z] = dt and algebra of right-invariant vector fields — by the basis

X = d x + yd z + zd t , Y = d y , Z = — [X,Y] = d z , T = — [X,Z] = d t .      (3.1)

Further, we fix on Engel group infinitely smooth nonnegative function ф : E — R supported in the unit ball such that E ф(g) dg = 1 .

For Q C E and u E L 1 _oc (Q) define mollification u ^e = u * ф _е , where u is u extended on E \ Q by zero.

Lemma 3.1. There are functions X ij E СО^ВфО)), i,j = 1, 2, such that

j Xij (g) dg = 5j, ij = 12,

(3.2)

E where 5ij is the Kronecker delta, and such that for every u E W^^Q), compact K C Q, g E K and 0 < e < dist(K, dQ)

Xu^e = (Xu) * X 11,e + (Yu) * X 12,e , Yu ' = (Xu) * X 21,e + (Yu) * X 22,e -      (3.3)

<1 We find functions X ij , i, j = 1, 2 , from the equations

Хф = XX 11 + YX 12 , Yф = XX 21 + YX 22 -

Using the expressions of the right-invariant vector fields (3.1) we obtain

^^

Хф = Хф - yZф - zTф = Хф - Z(уф) - T^ф)

= Хф - YX(уф) + XY(уф) + XYX(zф) - XXY(zф) - YXX(zф) + XYX(zф)

= X [ф + Y(уф) - YX(zф) + 2 YX(zф)] - Y [X(уф) + XX(zф)],

(; ф)

x

Yф = Yф + xZф + — Тф = Yф + Z (-ф) + T

= Yф+YX(хф) -XY(хф)+YXX

(ф)

-X Y ^X« ф)

-X Y ^X(l ф)

+XXY

■■)

=Y

ф + X (хф) + XX

(-- ф)|

-X

Y (хф) + 2 YX

(ф)-X Y (^ ф)].

The expressions in square brackets are the desired functions X ij , i,j = 1, 2 , for instance, X 12 = - X (уф) - XX(zф) . On the one hand, the functions are of the form

-^X"                   -^X"

Xij — ^ijф + Xaij + Ybij,  i, j — 1, 2, where 6ij is the Kronecker delta, aij,bij E C0”(Bi(O)). Since integrating by parts yields JE Xaij(g) dg = Je Ybij(g) dg = 0, the statement (3.2) of Lemma follows. On the other hand, from the expressions of χij and Lemma 2.2 it follows

ХфЕ = E (Хф)е = E (XX11)e + E (yX12)e = JCX11,e + YX12,e and in the same way Yфe = XX21,e + Yx22,£. This together with Lemma 2.1 leads to the statement (3.3) of Lemma. >

Lemma 3.2. Let u E W^^Q), p ф 1, K C Q be a compact, X1, X2, X3 be horizontal left-invariant vector fields. Then X1uε → X1u a. e. on K and

|| ^X 1 u ^{£ - X} 1 u || _p,K = ^{o (1)} ,    || ^X 2 ^X 1 u ^E ^ _P K = o (e),   ll ^X 3 ^x 2 ^x 1 u ^e ^ p,K = ⁰( ]: 2),

as e —^ 0.

<1 Any horizontal left-invariant vector field is a linear combination of basic vector fields, e. g. X i = aX + bY . For simplicity assume X i = X , the argument for X i = Y is the same and the general case is a linear combination of the two. By Lemma 3.1 we have Xu ^e = (Xu) * X ii,e + (Yu) * X i2,e and Je x ii = 1 , Je X 12 = 0 . By properties of mollifications Xu ^e — Xu as e — 0 a. e. and in L p (K ) . Next,

X 2 (Xu ^e ) = (Xu) * X 2 (X ii,e ) + (Yu) * X 2 (X i2,e ) = |(Xu) * (X 2 X ii ) e + |(Yu) * (X 2 X i2 ) e •

By properties of mollifications, e. g., (Xu) * (X 2 X ii ) e — 0 as e — 0 in L p (K ) . Analogously,

^X 3 X 2 ^{( X}u ^{e )} = —^{( Xu )} * ^{( X} 3 X 2 X ii ⁾ e ⁺ —^{( Yu )} * ^{( X} 3 ^X 2 X i2 ⁾ e , ε ²                            ε ²

where each expression after the ^ 2 term vanishes in L ^p (K) as e — 0 . >

In the next proof we use the following pointwise estimate for Sobolev functions:

Proposition 3.1 (see [12-14]) . Let K C Q be a compact. For every u E W ^i,p (Q) there is

0 C g E L ^p (K), such that

Iu(y) — u(z) I C d(y, z) (g(y) + g(z for a. e. y,z E V and |g|p,K C Cl Vhu|p,q. Moreover, the constant C is independent of u.

Lemma 3.3. Let u E W ^i,p (Q), v E L ^p (Q), X i , X 2 be horizontal left invariant vector fields, ^ E C Oo ° (B (0,1)), and K C Q be a compact.

• 1.    If p ^ 2, then for F _e (x) = (uv) * y _e (x) — u ^e (x)(v * ^ _e )(x) we have

• 2.    If p ^ 3, then for G _e (x) = (u ² v) * y _e (x) — 2u ^e (x)(uv) * ф _е (x) + (u ^e ) ² (x)(v * ф _е )(x) we have

IIF e||p/2,K = ^{O ( e )} ,    H ^X i F e b p/2,K = ^{o (1)} ,    ll^X 2 ^X i ^F e h p/2,K = o^) ’

(3.4)

as e —— 0.

^{| G} e h p/3,K = O ( ^e 2 ) ’    ^{| X} i G e h p/3,K = ^{O ( e )} ’    ll^X 2 ^X i ^G e h p/3,K = ^{o (1)} ’

(3.5)

as e — 0 .

< Let x E K , 0 < e < e o = 3 dist (x, dQ) , and K be an e o -neighborhood of K . For the summands in the expression of F _e (x) we have

(uv) * ye(x) = J u(z)v(z)^e (z ix) dz = JI u(z)v(z)^e (y ix)^e(z ix) dydz, к                  K xK

ue(x)(v * ^e)(x) = 11 u(y)v(z)^e(y-ix)^e(z-x) dy dz.

a x K

Thus,

(uv) * y _e (x) — u ^e (x)(v * y _e )(x) = JI ( u(y) — u(z) ) v(z)^ _e (y ⁱ x)^ _e (z ⁱ x) dydz. K x K

By Proposition 3.1 there is g E L ^p (K) , such that

^{u (}y) - ^{u ( z ) C} d(y, z) (g(y) + g(z))

and N^K ^ C II ^V H u ^ p, q . Since the term under the integral is nonzero only when d(x, y) ^ e and d(x, z) ^ e we get

| (uv) * V e (x) - u ^e (x)(v * V e )(x) |

^ 2Qe 11 ( g(y) + g(z) ) | v(z) | ^(y ^-i x) | V e (z ^-i x) | dydz

K xK

= 2Qe(ge(x)(|v| * Ы)(х) + (g|v|) * Ы(х)), where Q is the constant from the generalized triangle inequality. Next, using H¨older and Young inequalities we derive

|^{|( uv )} * V e - u ^{e (} v * V e ⁾|^| _{p/ 2} ,_K <  4Qe^Ig^I _p ,K ll ^{v |}l p,K ^H V e ||i <  e⁽4 ^Q C ||vIIi )HV h ^uII p,q|| ^vII p, q .

Since for the horizontal vector field X i we have X i V _e = | (X i V) _e , it follows

X i ((uv) * V e - u ^e (v * V e )) (x)

=e f f wy z-■—'         z-—¹

KxK

- u(z))v(z)((Xi^)E(y ix)Ve(z ix)

+ ^e(y ix)(XiV)e(z ix)) dydz, and from that

| X i ((uv) * V e - u ^e (v * w))(x) |

< ^{2 Q} JJ ( g⁽y⁾⁺ g ^{( z )})^{| v ( z )|}(^|( X i ^ ⁾ e ⁽ y ^-i x ^{)| |} V e C^{z -i} x ^)| K x K

+ ^ e (y ^-i x) ^| (X i v) e (z ^-i x) ^ dy dz

< ^{2 Q} ^ g *^{|( X} i ^ ⁾ _e ^| • ^{| v |}*^| V e ^{| + (}дМ ) *Ы • ll⁽ X i^elli

⁺ g ^e • ^{| v |}*^{|( X} i V ⁾ e ^{| +} g ^{| v |}*^{|( X} i У) е |)^{( х )} .

Again, by the H¨older and the Young inequalities we derive

^{|| X} i (^{(uv )} * y _e ^- u ^{e ( v} * V e ) ^ _{р/ 2} ,_к

^ ^{4Q H g H} p,K vll p,K

| (X i ^) e | i | V e | i +4Q | g|_p ^ | v |_{p R} | ^ e | i | (X i V) e | i p,p,

< ^{4 Q} (^| X r 0 ^| i ^| V ^| i ⁺ H ^ H i H X i v H i ) IIVh ^{u |} p,q ^{| v |} p,q .

The argument can be repeated for second derivatives giving

^{|| x} 2 X i (^{( uv )} * V e ^- u ^{e ( v} * V e)) ^|| _{p/ 2} ,_K

< 4Q (| X 2 X i ^ l i l v l i + | X i ^ | i I X 2 V l i + | X 2 ^ | i | X i V l i

^{+ |} 0 ^H i ^H X 2 ^X i V ^H i) IIVh u ^H p,Q ^H v ^H p,Q .

Thus, we obtain estimates uniform in e E (0, E q )

11X 1 F e W p^K = || X 1 (^{( uv )} * V e ^{— u}4^v * V e ⁾)|^| _{p/ 2} ,K <  C ll^V H u lWI v ll p.Q , |^{| eX} 2 ^X i F e |^| _{p/ 2 jK} = |^{| eX} 2 ^X i (^{( uv )} * V e ^— u ^{e ( v} * V e ) ) |^| _{p/ 2} ,_K <  C 11^V H ^u \ p,Q ^{| v} \ p,Q -

Note that for smooth functions u , v we have

X 1 (( uv) * V _e — u ^e (v * V _e ) ^ 0, eX ₂ X _i (( uv) * V _e — u ^e (v * V _e ) ^ 0

in Lp/2(K) as e ^ 0. Since smooth functions are dense in LP(K) and W 1,p(K) we can choose sequences of smooth un ^ u in W 1,p(K) and vn ^ v in LP(K) as n ^ to. The operator XiFe = XiFe(u,v) is linear in both u and v, which implies llX1Fe(u, v) \p/2,K < \X1Fe(u - un, v)\p/2,K + HXlFeCun, v — vn)\p/2,K + ||X1Fe(un,vn) Wp/2,K ^ C‘|VH(u — un) \p,Q + C'Hv — vn||p,Q + ||X1 Fe(un, vn) \p/2,K.

Therefore, lim ||X1 Fe(u, v)\p/2,K ^ C'||VH(u — un)|p,Q + C'Hv — vn\p,Q ^ 0, e >0

as n ^ to . Analogously, EX 2 X i F _e ^ 0 in L^{p /2} (K ) as e ^ 0 . The estimates (3.4) follow.

The estimates (3.5) are obtained in a similar way. For the terms in the expression of G _ε we have

(u2v) * Ve(x) =

Ш

u 2 (z)v(z)^ e (У 1 1 x)^ e (У 2 1 x)V e (z 1 x) dy i dy 2 dz,

z-■—'         z-—1         <-■—'

K x K x K

u ^e (x) • (uv) * V _e (x)

(u ^e ) 2 (x) • (v * V e )(x)

Ш

"—•      "—•      "—•

KxKxK

Ш

u(y i )u(z)v(z)^ e (У 1 1 x)^ e (y 2 1 x)V e (z 1 x) dy i dy 2 dz,

u(y i )u(y 2 )v(z)^ e (У 1 1 x)^ e (y 2 1 x)V e (z 1 x) dy i dy 2 dz,

"—•      "—•      "—•

K x K x K

thus

Ge(x)= JIT

<-V     <-V     <-V

K x K x K

(u(z) — u(y i)) (u(z) — u(y 2)) v(z)^ e (У 1 1 x)^ e (y 2 1 x)V e (z 1 x) dy i dy 2 dz-

Similar to what is already proved one can obtain the bounds

| G e | p/3,K <  CE ² |V h u | p, _Q | v | p,Q , | X 1 G e | p/3,K <  CE ^V h u | p, _Q | v | p,Q , ^X l G e W p^K <  C |V h u | p, _Q | v | p,Q .

Moreover, since for smooth functions u , v we have X 2 X i G _e ^ 0 as e ^ 0 in L p^/3 (K ) , using for threelinear operator G _e (u, u, v) arguments analogous to the ones given for F _e (u, v) one can prove that | X 2 X i G _e | _p/3,K ^ 0 as e ^ 0 . This concludes the proof of the estimates (3.5). >

The dual basis of 1-forms to the basis of left-invariant vector fields X, Y , Z, T is dx, dy,

Z = dz — x dy,

т = dt — xdz + ^ x2 dy,

and satisfies the dual relations

dZ = -dx Л dy, dT = -dx Л Z-

Lemma 3.4. Let f G W^^Q), p ^ 2, be a contact mapping. Then on any compact K c Q bZ(Xf£)llpAK = O(e), Z(Zf£> ^ Z(df (Z», bZ (Yf £)bp/2,K = O(e), bZ (Tf £)bp/2,K = o (I)

as e ^ 0 in L ^p/2 (K ).

<1 Since f is contact, we have

0 = Z(Xf) = Xf3 - fi Xf2, 0 = Z(Yf) = Yf3 - fi Yf2,

It follows Xf 3 = f i Xf i , Yf 3 = f i Yf i . Next, for the mollification f ^£ by Lemma 3.1

Z(Xf£) = Xf - fl Xf2

= (Xf) * Xii,e + (Yf3) * Xi2,e - fl(Xfl) * Xii,e - fi(Yf2) * Xi2,e(3.6)

= [ (f i XA) * X ii,£ - f iWi ) * X ii,£ ] + [ (f i Yf 2 ) * X i2, _e - flTO) * X i^ ] .

From Lemma 3.3 we have b Z ( Xf ^e )b _P/2,K = O(e) and similarly b Z ( Yf ^e )b _P/2,K = O(e) . Next, by the Cartan identity (see e. g. [15])

Z(Zf£) = Z([X, Y]f£> = XZ(Yf£} - YZ(Xf£) - dZ(Xf£, Yf ef(3 7)

Z (df (Z» = Z (WYf ]) = -dZ (Xf,Yf).

From the representation (3.6) and Lemma 3.3 it follows that the first two terms in (3.7) vanish as e ^ 0 in L ^p/2 (K) . Since dZ = - dx Л dy , by Holder inequality

dZ (Xf % Yf ^ = Xf£ Yf£ - Yf£ Xf£ ^ Xf Yfi - Yf2 Xfi = dZ (Xf, Yf)

as e ^ 0 in L ^{P/ 2} ( K ) . Finally,

Z(Tfe} = Z([X, z]f£) = XZ(Zfe} - ZZ(Xfex) - dZ(Xff Zf

= X(XZ(Yf£) - YZ(Xf£) - dZ(Xf,, Yf£)) - ZZ(Xf - dZ(Xf,, Zf£)

= XXZ (Yf^£) - 2XYZ(Xf^£) + YXZ (Xf^£) - XdZ (Xf^e, Yf^£) - dZ(Xf^e, Zf ^ef

From (3.6) and Lemma 3.3 it follows that the first three terms are o(£) as e ^ 0 in L ^p/2 (K) . By Lemma 3.2 and the Holder inequality the last two terms are also o( 1) as e ^ 0 in D ^p/2 (K ) . The lemma is proved. >

Lemma 3.5. Let f G WlO’Cp(Q), p ^ 3, be a contact mapping. Then on any compact K c Q bT (Xf £^bp/3K = O(e2),   bT (Zf £^bp/3K = O(e), bT(Yf£)||pAK = O(e2), t(Tf£) ^ t(df (T»

as e ^ 0 in L ^{p/ 3} ( K ) .

< Since f is contact, we have

0 = Z ( Xf ) = Xf 3 - f i Xf 2 , 0 = t ( Xf } = Xf 4 - f i Xf 3 + 2 f l Xf 2 .

It follows Xf 3 = f i Xf and Xf = 2 f 2 X/ 2 . Next, for the mollification f^e by Lemma 3.1

т{Xf ^ = Xf4 - f£ Xf3 + 2 f)2 Xf2 = Xf^^ + Yf4*X12,£

— f f ( Xf 3 * X ii,_e + Yf 3 * X i2,_e ) + 2 ( ff ) 2 ( Xf 2 * X ii,_e + Yf 2 * X 12,e )

V1        \                                     1      9             "I             (3.8)

= (2 f^Xf2) * X 11,f — f i (f 1 Xf 2 ) * X 11,£ + 2 ( f l ) Xf 2 * X 11,£

+ [(2 f l ² Yf 2) * X 12,f — f l ( f 1 Yf 2 ) * X 12,_e + 2 ( f tf Yf 2 * X 12,ej •

Be Lemma 3.3 we have ||t { Xf^e )| р/з,к = O(£ ² ) and similarly ||t { Yf ^£ )| _р/з,к = O(£ ² ) as £ ^ 0 .

Next, by the Cartan identity (see e. g. [15]) we have т{Zf£) = т([X, Y]f£> = Xt{Yf£> - Yt{Xf£) - dT{Xf f Yfe\         (3.9)

From the representation (3.8) and Lemma 3.3 it follows that the first two terms are O(£ in L ^p/3 (K) , as £ ^ 0 . Next, since dT = - dx Л Z , we have

dT{Xff Yf£) = -Xf£ Z{Yf£} + Yf! Z{Xf£}.                 (3.10)

Applying Lemmas 3.2, 3.4 and the Holder inequality we obtain | dT { XffYf ^£ )| _р/з,к = O ( e ) , as £ ^ 0 . Next,

T{Tf£) = т([X, Z]f£) = Xr{Zf^ - Zr{Xf^ - dT{XfE, Zf£).

Let us estimate each term. From (3.9) and (3.10) we have

Xt { Zf ^£ ) = XXt {Yf ^£ ) - XYt { Xf ^£ >

(3.11)

+XXf££ Z{Yf £{ + Xf£ XZ{Yf£) - XYfi£ Z{Xf £{ - Yf£ XZ{Xf£).

From (3.8) and Lemma 3.3 it follows that the first two summands in (3.11) and also Zt {Xf^eX) vanish in L ^p/3 (K) . Applying Lemmas 3.2, 3.4 and the Holder inequality we can conclude that the last four summands, in (3.11) also vanish in L ^p/3 (K) . Finally, using Lemmas 3.2, 3.4 and the H¨older inequality we conclude

- dT { Xf ^£ , Zf ^£ ) = dx Л Z { Xff Zf ^£ ) = X" ¹ Z{Zf ^£ ) - /■ ¹ Z { Xf ^£ ) ^ Xf Z {d f { Z » - 0

as £ ^ 0 in L ^p/3 (K) . The only thing left to note is that

т (df {T)) = т (^[X^^f.dff {Z)]} = -dT (Xf,df {Z)) = dx Л Z (Xf^df {Z)) = XfZ (df {Z ^\

Thus, т {T f ^£ ^ ^ т {^d f { T )^ , as £ ^ 0 in L ^p/3 (K ) . The lemma is proved. >

Define homogeneous weight of the basic left-invariant 1-form by

a(dx) = a(dy) = 1, a(Z) = 2, o(t ) = 3.

<1 Proof Of Theorem 1.1. For the forms of the weight 1 (i. e. looking like adx + bdy , a,b E R ) the statement of the Theorem immediately follows from Lemma 3.2, for the forms of the weight 2 ( cZ , c E R ) it follows from Lemma 3.4, and for the forms of the weight 3 ( ст , c E R ) from Lemma 3.5. >

4.    Applications

g G Q , ^ 1 ,..., ^ k G T g E . Note that f # (ш 1 Л Ш 2 ) = f # Ш 1 Л f # Ш 2 , and for basic left-invariant forms                  f # dx = Xf i dx + Yf i dy, f # Z = d f { Z } Z,

f #dy = Xf2 dx + Yf2 dy,  f #t = df {T) T.

The notion of the homogeneous weight can be extended on k-forms by the rule a(wi Л Ш2) = a(wi) • ^(^2). Next, we consider differential forms with terms of the maximal homogeneous weight. On Engel group such forms are ш1(д) = a(g)T, ш2(д) = a(g)Z Л T,                                                (4.1)

ш3(д) = (ai(g) dx + 02(g) dy) Л Z Л t,

ш4(д) = a(g) dx Л dy Л Z Л t, and have the weights a(wi) = 3, ст(ш2) = 5, ст(шз) = 6, ст(ш4) = 7.

An analogue of the next theorem was proved for 2-step the Carnot groups in [2, Theorem 3.5] and for arbitrary the Carnot groups in [6, Theorem 4.3].

Theorem 4.1. Let Q, Q ‘ C E be open, ш be a k-form on Q ‘ of the form (4.1) with the coefficents of the class C (Q ‘ ) П L ^ (Q ’ ), k = 1,..., 4, and f : Q ^ Q ‘ be a contact mapping of the class W^^Q), p ^ а(ш). Then

(f^ш ^ f #ш, as e ^ 0 in Lp°(\Q).

• <1 It suffices to prove the theorem for the forms ш ( у ) = a(y)^(y) , where a G C (Q ’ ) n L ^ (Q ’ ) , and ξ is a basic k -form. For basic 1-forms we have

(fe)*dx = df = Xfi dx + Yfl dy + Zfi Z + Tf1 t,

(fe)*dy = df2 = Xf2 dx + Yfi dy + Zf2 Z + Tfi t,

(fe)*Z = Z(Xfe) dx + Z(Y^fe) dy + Z(Zfe) Z + Z(Tf t,

(fe)*T = t{Xfe) dx + t{Yfe) dy + t{Zfe) Z + t{Tfe) t.

Therefore, by Theorem 1.1 on each compact K C Q , as e ^ 0 we have

(fe)*dx = f #dx + o(1) dx + o(1) dy + o

(fe)*dy = f #dy + o(1) dx + o(1) dy + o

(ey+o^

( e ) Z+o ( 1 )

t in L ^p (K),

t in L ^p (K),

(f£)*Z = f #Z + O(e) dx + O(e) dy + o(1) Z + o Q) t (fe)*t = f#t + O(e2) dx + O(e2) dy + O(e) Z + o(1) t in Lp/2(K), in Lp/3(K).

Thus, as e ^ 0

(fТт ^ f # t in L p/3 (K),

(fT (Z Л т) ^ f # (Z Л т ) in L p/5 (K ),

(f ^f ) * (dx Л Z Л т) ^ f # (dx Л Z Л т) in L p/6 (K ),

(f ■ (dy Л Z Л т) ^ f # (dy Л Z Л т) in L p/6 (K),

(ff)*(dx Л dy Л Z Л т) ^ f #(dx Л dy Л Z Л т) in Lp/(K).

From that for the basic k -form £ of the weight a(^ ) = а(ш) we get (f ^e ) * £ ^ f # £ in L p -^ (K ) as e ^ 0 . Sinse a(y) is continuous and bounded, the composition a о f ^f is uniformly bounded and converges to a о f a. e. on K as e ^ 0 . Hence, by Lebesgue theorem (f ^e ) * ш ^ f # ш in L p "'^ ( k ) as e ^ 0 . ▻

Horizontal vector field on Q C E is a mapping V : Q ^ H E , V = v i X + V 2 Y . Weak ( horizontal ) divergence div H V of the horizontal vector field V G L ₁ ¹ _oc (Q) is a function h G L ¹ _oc (Q) , such that for every у G C 0 ” (Q)

j V^(g) dg =

Ω

j MgMa) dg.

Ω

It follows that divHV = Xvi + Yv2 pointwise for V G C1 (Q) and distributionally for V G W^^Q). If to the vector field V = viX + V2Y we assign the dual 3-form ш = (v1 dy — v2 dx) Л Z Л т,

(4.2)

then

dш = divH V dx Л dy Л Z Л т = divH V dx Л dy Л dz Л dt.

An analogue of the next theorem is proved for 2-step the Carnot groups in [5, Corollary 2.15] and for arbitrary the Carnot groups in [6, Theorem 4.24].

Theorem 4.2. Let Q, Q ‘ C E be open, ш be a horizontal 3-form on Q ‘ of the form (4.2) with the coefficents v i ,V 2 G W ^1,“ (Q ‘ ). If f : Q ^ Q ‘ is a contact mapping of the class W OJ CQ), and fQ) C Q ‘ , then

f #dш = df #ш in the weak sense.

• <1 Step 1. If ш G C 1 (Q ‘ ) , then for each ^ G C 0 ^ (Q) we have

j (fe)*dш • ^ = j d^f е)*ш • ^ = (—1)k+1 j (fе)*ш Л d^.

ΩΩ   Ω

By Theorem 4.1 as e ^ 0 we obtain jf#dш • ^ =

Ω

( —1)k+1 j f #ш Л d^ = j d(f #ш)

• V.

ΩΩ

Step 2. Now let ш = v1 dy — v2 dx Л Z Л т be as in the conditions of the theorem. Define Ve = v[X + v2Y and ше = (vf dy — v2, dx Л Z Л т. By step 1 for each у G C0^(Q) we have f#dωε

Ω

• V = ( —1)k+1

j f #ше Л dy.

Ω

(4.3)

Since Vj are continuous and bounded, compositions vjof2 are uniformly bounded and converge to Vj o f a. e. on Q. Therefore, be Lebesgue theorem f#ωε

Ω

A d^ —— j*

f #ш A d^

as E — 0. On the other hand f #dw2 = f # (divH V2 dx A dy A Z A т) = divH V2 o f • det df • dx A dy A Z A t.

By the properties of convolutions div H V ₂ (y) is bounded uniformly in e >  0 and

divH Ve(y) = Xvf(y) + Yv^(y) — Xvi(y) + Yvi(y) = divH V (y)

as E — 0 for y E f (Q) \ X , where X is some null set. By the change of variables formula [11, Theorem 5.4] det df = 0 a. e. on f ^-1 (X) . Therefore,

(Xvf + Yv2) o f (x) • det df (x) — (Xv1 + Yv2) ◦ f (x) • det df (x)

for a. e. x E Q. Hence, by Lebesgue theorem jf#d^2•^ =

Ω

j ^(x) divHV2(f (x)) det df (x) dx — j f #dw • у

Ω

Ω as e — 0. All in all, we can go to the limit as e — 0 in both sides of the equation (4.3). The theorem is proved. >

Theorem 4.2 extends on Engel group the theorems [5, Theorem 2.6, 2.14] proved for 2-step case. In [5, Remark 2.19] it is noted the these are the only theorems in the paper that rely on 2-step structure of the Carnot group. Thus, results of the paper [5] can be translated on Engel group without changes.

The mapping f : G D Q — G on a Carnot group G is the mapping with bounded distortion if f E W iO’V (Q) and for some K >  0

|dHf (x) |v < K det df (x)

for a. e. x E Q . The least constant K is called the outer distortion coefficent and is denoted K o (f ) .

Corollary 4.1 [5, Theorem 4.10] . Let Q C E, f : Q — E be a mapping with bounded distortion. Then

• 1)    f is locally Holder continuous;

• 2)    f is Pansu differentiable a. e.;

• 3)    f has Luzin N-property;

• 4)    a certain change of variable formula holds: if D C Q is a compact, | dD | = 0, and u is a measurable function on E, then function u(y)^(y, f, D) is integrable on G iff is u(f (x)) J (x, f ) integrable on D, moreover

  u ( f ( x )) J ( x, f ) dx

  D

  
  

  j ^{u (}y⁾^⁽y ^{,f,D )} dy.

  G

  
  

  Next, let

  
  

  G(x) =

  
  

f( det dff (x)) v (dH f (x)TdH f (x)) 1I Id,

---- if det df (x) > 0, otherwise.

The matrix G(x) is symmetric and characterizes the local deviation of f from a conformal mapping. The matrix G(x) defines the mapping

ν - 2

A(x, £) = (G(x)£, ^ ~G(x) £, x e Q, £ G HG, satisfying the conditions l^TnК|v < (A(x.€).€) < CvKo(f)v-1|£|v, CvKO (J )

where C _ν is a constant independent of f .

Corollary 4.2 [5, Corollary 4.8] . Let Q C E, f : Q ^ E be a mapping with bounded distortion. If w is a W _l ¹ _o ^, _c ^∞ -solution to the equation

— div H^ jV H w | ⁵ V H w^ =0

in an open domain W C E, then v = w о f is a weak solution to the equation

—divH A (x, VHv) = 0

on f ^-1 (W) П Q.