Мониторинговые наблюдения метеорного эха на радаре EKB ИСЗФ СО РАН: алгоритмы, валидация, статистика

Исследования метеорных потоков актуальны для решения задач астероидно-кометной опасности.

Изучение метеорных потоков и отдельных метеоров позволяет исследовать связь метеорных потоков с родительскими телами (астероидами и кометами) и тем самым изучать динамику мелких тел в Cолнечной системе. В приложении к физике верхней атмосферы метеоры выступают источниками возмущений фоновой атмосферы и позволяют исследовать процессы генерации мелкомасштабных неоднородностей, а также их динамику под действием фоновых процессов в верхней атмосфере. Одним из наиболее распространенных способов использования метеоров для диагностики верхней атмосферы является исследование скорости нейтрального ветра. Абляция метеоров происходит на высотах от 60 до 150 км в зависимости от массы метеороида, его скорости и т. д. [McKinley, 1961; Briczinski et al., 2009]. Происходящие при этом процессы — от свечения и ионизации (для мелких метеоров) до электрофонного эффекта и ударной волны (для крупных болидов) — многообразны и сложны [Janches et al., 2009; Berngardt et al., 2013] и находятся в стадии изучения [Zhu et al., 2016]. При этом массивные метеороиды могут аблировать лишь частично, достигая поверхности Земли. Более мелкие метеоры аблируют в атмосфере практически полностью, позволяя по динамике абляции оценить массу метеороида.

Одним из распространенных методов наблюдений за метеорами являются радарные наблюдения. При радарных наблюдениях выделяют два типа рассеянного сигнала по виду рассеивающего объекта: рассеяние на зоне повышенной ионизации вблизи метеороида (head-echo) [Li et al., 2020] и рассеяние на метеорном следе (trail-echo). Метеорные следы представляют собой вытянутые ионизированные неоднородности в нижней ионосфере (на высотах ниже 150 км), рассеяние на которых обладает ракурсными свойствами [McKinley, 1961] , поэтому их наблюдения требуют сравнительно невысокого потенциала радара. Геометрия таких наблюдений представлена на рис. 1, а .

Рассеяние от области вблизи метеороида более изотропно, его сечение меньше сечения рассеяния на метеорном следе, поэтому для изучения head-echo необходимы достаточно высокопотенциальные радары. К таким высокопотенциальным радарам можно отнести радары MU [Kero et al., 2012] , ALTAIR [Close et al., 2002] , а также большинство радаров некогерентного рассеяния (Millstone Hill [Erickson et al., 2001] , EISCAT [Szasz et al., 2008] , Arecibo [Mathews et al., 2003] ). С помощью исследований head-echo решаются траекторные задачи, касающиеся метеорных потоков и их источников. В этом случае экспериментально возможно непосредственное определение траектории, скорости входа в атмосферу и скорости замедления тела [Mathews et al., 2003, 2010; Szasz et al., 2008] , что позволяет судить о его массе и направлении радианта.

Другим способом анализа радианта являются ракурсные свойства метеорного следа [Lovell, 1954; Jones et al., 2005; Campbell-Brown, 2008] . По соотношению плазменной частоты ионизированного следа и частоты зондирующего сигнала метеорные следы в основном подразделяют на underdense и overdense [Parris, 2003] , причем первым соответствуют менее массивные, а вторым — более массивные метеороиды. Существует также промежуточный тип метеорных следов, на радарах SuperDARN обычно не исследуемый.

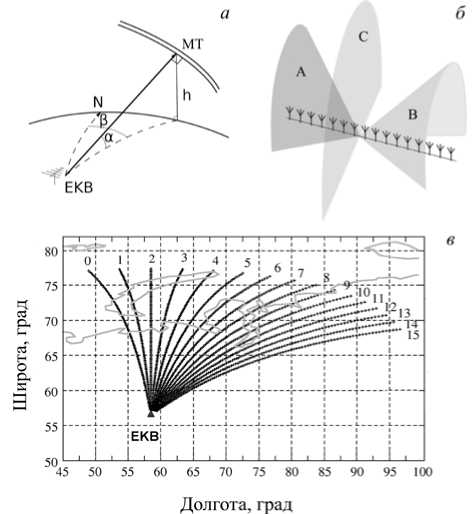
Рис. 1 . Схема обратного рассеяния на метеорном следе МТ ( а ): α и β — угол места и азимут соответственно. Поверхности излучения радара EKB ( б ): А и В — для случая сканирования на любом возможном луче; С — при излучении строго перпендикулярно антенной решетке. Сектор обзора радара EKB ( в ); числами обозначены порядковые номера лучей

Очевидно, что менее массивных метеоров больше и поэтому они чаще используются в практических задачах исследования верхней атмосферы. Сформировавшийся после абляции такого метеора след — вытянутая ионизированная область, которая, с одной стороны, рекомбинирует, а с другой — расплывается под действием амбиполярной диффузии [Jones, Jones, 1990] , поэтому электронная концентрация в следе падает со временем. В результате этого рассеяние на underdense следе характеризуется экспоненциальным спадом мощности принимаемого сигнала. Скорость спада связана с коэффициентом диффузии, что позволяет этот коэффициент непосредственно измерять. Кроме того, след находится в достаточно плотной атмосфере, поэтому под действием ион-нейтральных столкновений увлекается нейтральным ветром. Это дает возможность измерения нейтрального ветра на высотах наблюдения метеорных следов [Nakamura et al., 1991; Hall et al., 2006] , и, при использовании плотных сетей инструментов, например сетей метеорных радаров [Deegan et al., 1970] или радаров SuperDARN [Hall et al., 1997] , позволяет изучать движение верхней атмосферы в режиме мониторинга в большом пространственном регионе.

Важной задачей мониторинговых метеорных исследований являются алгоритмы автоматического детектирования и определения параметров метеорного эха. Алгоритмы для работы с рассеянием на метеорных следах, как правило, сводятся к анализу хода мощности принятого сигнала и поиску резких пиков с экспоненциальным спадом, что является характерным признаком underdense эха [Tsutsumi et al., 1999]. Детектирование метеорного эха на рада- рах SuperDARN может проводиться как по средним корреляционным характеристикам сигнала [Jenkins, Jarvis, 1999], так и посредством анализа либо формы рассеянного сигнала одиночного импульса в режиме повышенной частоты оцифровки [Parris, 2003], либо квадратурных компонент рассеянного сигнала, представляющего собой сложную импульсную последовательность [Yukimatu, Tsutsumi, 2002].

В данной работе рассматриваются реализация алгоритма автоматического поиска метеоров на радаре EKB ИСЗФ СО РАН по квадратурным компонентам сигнала, решение обратной задачи восстановления вектора скорости нейтрального ветра по полученным данным и проводится валидация указанных алгоритмов.

РАДАР EKB ИСЗФ СО РАН

Радар EKB ИСЗФ СО РАН представляет собой декаметровый загоризонтный радиолокатор типа CUTLASS, разработанный и произведенный в Университете Лейстера (UK), аналогичный радарам сети SuperDARN. Радар расположен в Свердловской области РФ (56.5° N, 58.5° Е). Сектор обзора радара шириной около 52° по азимуту делится на 16 направлений (лучей) шириной 3°-6° в зависимости от зондирующей частоты. Центральная ось сектора обзора радара имеет азимут 19°. Сектор обзора радара и ориентация его лучей показаны на рис. 1, б . Радар функционирует в диапазоне частот 8–20 МГц, обеспечивая разрешение по дальности в стандартных режимах 15–45 км и максимальную дальность 3000– 4500 км. Радар EKB является стереорадаром, т. е. может работать на двух разнесенных несущих частотах и разных лучах одновременно. Антенная решетка радара EKB линейна и обладает существенным задним лепестком в наиболее часто используемом диапазоне частот 10–12 МГц, поэтому сечение диаграммы направленности каждого луча можно рассматривать как поверхность конуса. Характерный вид сечения диаграммы направленности для различных лучей приведен на рис. 1, б .

Стандартным режимом работы радара является излучение многоимпульсных (голомбовских) последовательностей [Berngardt et al., 2015] , обеспечивающих одновременно высокое пространственное и спектральное разрешение. Последующие автокорреляционная обработка сигнала, накопление автокорреляционной функции (порядка 4–6 с) для каждого выбранного луча и анализ амплитудно-фазовой структуры усредненной автокорреляционной функции позволяют определять средние характеристики сигналов, рассеянных как ионосферой, так и земной поверхностью [Ribeiro et al., 2013] .

Наиболее распространенным в сети SuperDARN способом работы с метеорным эхом является анализ характеристик усредненных автокорреляционных функций: мощности, дальности, доплеровской скорости вдоль луча зрения и спектральной ширины. Селекция производится на основе статистических порогов этих параметров, определенных экспериментально по совместным измерениям с метеорными радарами. Разрешение по времени данных методик соответствует времени накопления автокорреляционной функции и составляет обычно 4–6 с [Arnold et al., 2003]. Существуют также алгоритмы как полного цикла детектирования и определения параметров рассеяния [Yukimatu, Tsutsumi, 2002], так и селекции рассеяния на метеорных следах с последующим определением параметров рассеяния по данным FitACF [Parris, 2003], анализирующие сырой сигнал в виде квадратурных компонент.

АЛГОРИТМ ПОИСКАИ ОЦЕНКИ ПАРАМЕТРОВ МЕТЕОРНОГО ЭХА

Общее описание алгоритма

Как было указано ранее, стандартные измерения на радаре ведутся при помощи сложных многоимпульсных зондирующих последовательностей, позволяющих рассматривать радар как импульсный радар с длительностью зондирующего сигнала 0.3 мс и с неравномерным периодом повторения импульсов. При этом разрешение радара по времени переменно с минимальным периодом повторения 2.4 мс (минимальный межимпульсный интервал) в стандартных режимах. Регистрация квадратурных компонент рассеянного сигнала ведется после начала каждой зондирующей последовательности с периодом оцифровки 0.3 мс, что позволяет обеспечить разрешение измерений по дальности 45 км.

В связи с импульсной схемой работы радара и большим диапазоном дальностей некоторую проблему составляют межипульсные помехи (cross-range interference, CRI), возникающие, когда мощный сигнал с большей дальности от одного импульса затеняет сигнал последующего импульса с меньшей дальности, и наоборот [Yukimatu, Tsutsumi, 2002] . Метод очистки данных от CRI, детально описанный в работе [Yukimatu, Tsutsumi, 2002] , был применен в нашем алгоритме для улучшения получаемых данных.

Обработка метеорных сигналов включает две последовательные задачи: 1) детектирование рассеянного сигнала и определение дальности до рассеивателя; 2) определение параметров рассеянного сигнала: амплитуды, характерного времени жизни, доплеровской скорости. Рассмотрим решение этих задач на радаре EKB.

Детектирование кандидата на метеорное рассеяние

Принятый сигнал регистрируется в виде квадратурных компонент, однако, поскольку мы рассматриваем амплитудные (пиковая мощность, характерное время жизни) и фазовые (доплеровская скорость) параметры сигнала независимо, удобнее перейти к амплитудной A ( R_k , t ) и фазовой ϕ( R_k , t ) разверткам сигнала, где R k — k -я радиолокационная дальность (при приеме радар накапливает сигнал в течение некоторого времени (100–300 мкс), тем самым разбивая пространственную развертку сигнала на дискреты (15–45 км), соответствующие пространственному разрешению радара); t — время.

Время наблюдения метеорного следа может достигать нескольких секунд [Tsutsumi et al., 1999] , поэтому необходимо рассматривать совместно несколько следующих друг за другом зондирующих последовательностей, так как типичная длительность последовательности составляет 0.1–0.2 с. Необходимо учитывать также неэквидистантность применяемой импульсной последовательности. Таким образом, временной ход разверток удобно представить в виде дискретной последовательности t_{l , n} , где l — номер импульса внутри последовательности; n — номер последовательности. Например, A ( R ₁₀, t _3,4) — амплитуда отклика от 3-го импульса 4-й последовательности на 10-й дальности.

Для того чтобы быть принятым в качестве кандидата на метеорное рассеяние, сигнал должен удовлетворять следующим условиям (этапам проверки):

Этап 1. Высокая амплитуда всплеска . Метеорные следы — относительно редкие, сравнительно короткоживущие и почти не меняющие положения в пространстве объекты. Нас интересуют всплески высокой амплитуды, по которым можно уверенно определить остальные параметры метеорного эха — время жизни и среднюю скорость, поэтому мы будем вести поиск по простому превышению амплитуды над уровнем шума. Поскольку в пределах времени жизни следа радиолокационная дальность R k не зависит от времени t l , n , поиск метеорного рассеяния можно проводить на каждой фиксированной дальности R k независимо, по условию краткосрочного превышения амплитудой сигнала уровня шума на 6 дБ:

A ( R k , t o, n ) >  M , (1)

где M — уровень шума, измеренный радаром перед началом цикла сканирования +6 дБ.

Все точки A ( R k , t 0, n ), удовлетворяющие (1), являются всплесками достаточно высокой амплитуды и переходят на следующий этап анализа.

Этап 2. Высокая пространственная локализация . Метеорные следы — объекты редкие и сильно локализованные в пространстве. Поэтому для каждого всплеска амплитуды, найденного на этапе 1, проверяется выполнение второго условия — пространственной локализации всплеска амплитуды. Для этого средний уровень на смежных к искомой дальности R_k дальностях R_{k –1}, R_{k +1} не должен превышать порогового значения M :

A ( ^Rk + 1 , 1 0, n ) + A ( ^Rk - 1 , 1 0, n ) _M --------^;------------^;— <  M .

Все точки A ( R_k , t _{0, n} ), удовлетворяющие (2), являются пространственно-локализованными всплесками амплитуды и переходят на следующий этап анализа.

Этап 3. Монотонный спад амплитуды сигнала. Как уже упоминалось, основной особенностью рассеяния на underdense следах является экспоненциальное убывание амплитуды сигнала во времени. Поэтому при детектировании метеорного эха мы ищем ряд всплесков с монотонно убывающей во времени амплитудой. Наличие шума и случайных вариаций амплитуды затрудняет работу такого алгоритма, поэтому мы анализируем точки, разделенные достаточно большим промежутком времени, на котором эти шумоподобные эффекты значительно слабее основного монотонного убывания. Такой характерный промежуток в нашем алгоритме выбирается равным длине зондирующей последовательности, что составляет от 100 до 200 мс в зависимости от типа последовательности. Таким образом, перебираются по времени t0, n+l отклики от первых импульсов последовательностей, следующих за обнаруженным на предыдущем этапе всплеском амплитуды. Из тех последовательностей, для которых амплитуда сигнала от первого импульса удовлетворяет условию (1) и первые отсчеты которых убывают во времени каждые 100–200 мс (соответствие условию (2) не проверяется):

A ( R k , 1 0, n + m ) >  A ( R k , 1 0, n + m + 1 ), M = 0... » - 1, (3) формируется набор из s последовательностей S ( R k , t 0, n , s ), используемых для дальнейшего анализа в качестве кандидатов на метеорное рассеяние.

Формирование набора завершается, если прекращается выполнение либо условия (1), либо условия (3).

За время сканирования может быть сформировано несколько таких наборов S ( R k , t 0, n , s ), каждый из которых в дальнейшем обрабатывается отдельно. В текущей реализации алгоритма последовательности, попавшие на данном этапе в какой-либо набор, не исключаются из проверки остатка данных и могут впоследствии сформировать еще один набор.

Для уменьшения влияния шума из полученного набора S ( R k , t 0, n , s ) исключаются точки, не удовлетворяющие условию

A ( R k , t , , n ) >  M . (4)

На рис. 2, a приведен пример выделенной последовательности амплитуд A ( R k , t l , n ) на фиксированной дальности R_k , соответствующей метеорному эху.

Определение параметров рассеянного сигнала

Основными параметрами underdense рассеяния на метеорных следах являются: координаты точки рассеяния, характерное время жизни следа и доплеровская скорость вдоль луча зрения. Знание координат точки рассеяния важно для исследований диффузионных процессов в верхней атмосфере и тонкой структуры атмосферного ветра на высотах абляции. Временной ход амплитуды обратного рассеяния на underdense следе в первую очередь связан с расплыванием следа под действием амбиполярной диффузии, и таким образом характерное время затухания экспоненциального эха может быть непосредственно связано с коэффициентом диффузии [Jones, Jones, 1990] . Наблюдаемые на радаре EKB метеоры аблируют на высоте ниже 110 км, где, с одной стороны, нейтральная компонента достаточно плотна, чтобы вызвать абляцию, а с другой стороны, ионы не за-магничены и их движение в основном контролируется нейтральным ветром. На не анализируемых нами высотах больше 110 км, где ионосферная плазма замагничена, дрейфы определяются перекрестными электрическим и магнитным полями в ионосфере.

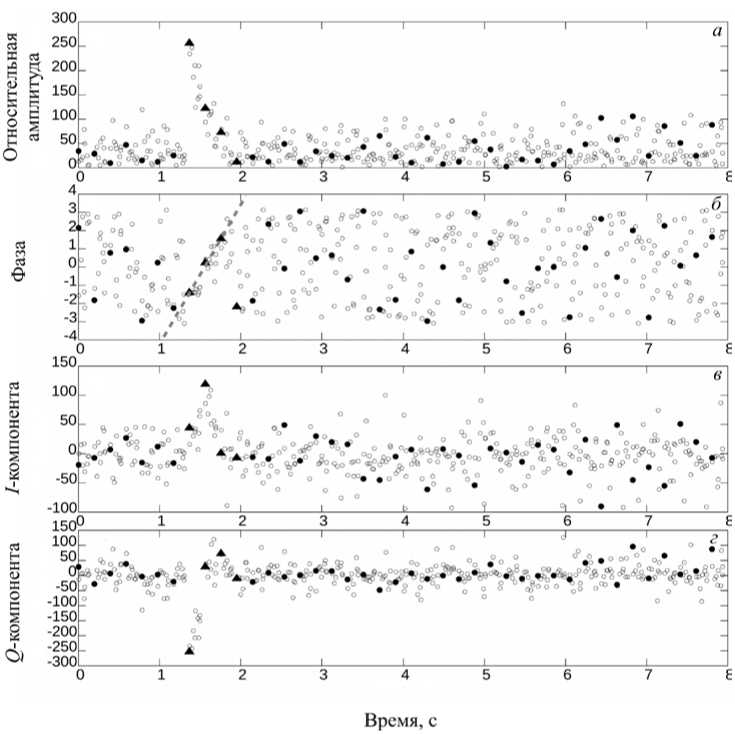
Рис. 2 . Пример хода амплитуды ( a ), фазы ( б ) и квадратурных компонент ( в , г ) сигнала на фиксированной дальности R_k при наличии метеорного рассеяния. Черными треугольниками обозначены первые импульсы выделенных в рамках задачи 1 последовательностей, черными кругами — первые импульсы остальных последовательностей в рамках цикла сканирования, окружностями обозначен сигнал от всех остальных импульсов

Предполагается, что за время существования эха скорость и направление нейтрального ветра не могут существенно измениться и доплеровское изменение фазы сигнала в первом приближении линейно, что позволяет непосредственно измерять скорость ветра вдоль луча зрения [Tsutsumi et al., 1999] по изменению фазы принятого сигнала в наборе сеансов зондирования. Таким образом, последовательность рассеянных сигналов, удовлетворяющая требованиям (1)–(3), используется для решения обратной задачи — определения характеристик метеорного эха. Задача решается методом наименьших квадратов раздельно для амплитудной A ( R k , t ) и фазовой ϕ( R k , t ) разверток сигнала.

Для моделирования сигнала используется хорошо известная модель [Parris, 2003] экспоненциального убывания амплитуды и линейного хода фазы:

f _ t

A m ( t ) = 9( t ) A o e " ^T; (5) Ф m ⁽ t ) = 9⁽ t ⁾⁽ st + Ф о ^).

Здесь A ₀ — начальная амплитуда рассеянного сигнала; τ — характерное время жизни; s — линейный набег фазы, соответствующий доплеровскому сдвигу частоты; ϕ 0 — начальная фаза; θ( t ) — функция Хэвисайда (единичная ступенчатая функция).

Однако последовательности в рамках одного цикла сканирования не синхронизированы во времени, т. е. задержка между излучением последнего импульса предыдущей последовательности и первого импульса следующей является случайной величиной и не может быть определена в рамках существующей системы управления радара EKB. В результате между соседними последовательностями, попадающими в набор для фитирования, появляется не определяемый в рамках системы набег фазы, что в случае набора из двух и более последовательностей приводит к катастрофическому ухудшению качества определения доплеровской скорости и к искажениям при определении характерного времени жизни. Для компенсации аппаратно-программных особенностей радара EKB необходима модификация модельной функции. Поскольку задержка между последовательностями не определена, то мы можем использовать только среднее значение данной задержки по циклу сканирования.

Поскольку вариации задержки между последовательностями малы, при расчете амплитуды мы их не учитываем. Для удобства дальнейших расчетов времени жизни мы логарифмируем амплитуду принятого сигнала, что позволяет определять амплитуду из известного уравнения линейной регрессии.

Фазу, в предположении линейного набега фазы, можно представить как кусочно-заданный набор линий одинакового наклона с неопределенными начальными фазами. Модифицированная модель сигнала выглядит так:

ln( A m ( t l , n )) = ln( A o )

^Ф m (t l , n ) = st l , n + ^Ф n ,

;

τ

где l ϵ0… N p — номер импульса внутри последовательности; n ϵ0… N_s — номер последовательности в наборе-кандидате; N_p — число импульсов в последовательности; N_s — число последовательностей в наборе-кандидате.

Поиск значений параметров модели τ и ( s , ϕ n ) ведется методом наименьших квадратов как независимая минимизация функций невязки:

^ aC A ) , T) =

Экспериментально измеренные на основе данных, собранных за 16 сут, соответствующих прохождению максимумов шести метеорных потоков в период с января по август 2016 г., распределения σ _{A , r} и σ ϕ приведены на рис. 3, a , б соответственно. Выбор метеорных потоков для анализа позволяет эффективно оценить количество ошибочно определенных метеоров и более уверенно доверять результатам валидации модели.

Как видно из рис. 3, можно использовать два качественных порога для дополнительной проверки валидности полученных данных:

[c A, r <  0.5;

[° Ф < 0.7.

^Np N s              t

= 22 ^ln( A o) —,—^ln ( A ( R k , t i l = 0 n = 0               ^T

N

N s

П_ф ⁽ s , Ф о ,..., ^ф N s ) =

l , n

= min,

N p N s

= 22 st i , n ^+ф n ^-ф ( R k , t i , n ) = min. l = 0 n = 0

Вследствие линейности модели по искомым параметрам (начальная амплитуда A 0 и начальные фазы отрезков ϕ _n , характерное время жизни τ и наклон фазы s ) задача решается аналитически.

Порог для σ _{A , r} ограничивает большую часть распределения ошибок аппроксимации моделью экспериментальной амплитуды. Порог для σ ϕ выбран из соображений допустимой ошибки определения доплеровской скорости: отклонение 0.7 рад/с соответствует ошибке в определении скорости метеорного следа порядка 2 м/с для частоты 8 МГц, что критично при наблюдениях ветра, скорость которого составляет порядка ±20 м/с. Наблюдения, имеющие σ ϕ большую, чем порог, не удовлетворяют нашим требованиям к точности определения скорости и отбрасываются. Из рис. 3, б видно, что введение второго порога ощутимо уменьшает (на 57 %) количество случаев, пригодных к интерпретации. Метеоры, соответствующие σ ϕ >0.7, в работе нами не рассматриваются.

АДЕКВАТНОСТЬ МОДЕЛИ

Важными вопросами являются адекватность модели экспериментальным наблюдениям и влияние шума на точность определения параметров. Характерной величиной, позволяющей оценить адекватность модели экспериментальным данным, является невязка между моделью и экспериментом. Нами были раздельно проанализированы распределения невязки модели по амплитуде и по фазе на основе набора данных, полученных в 2016 г.

Нормированная ошибка найденного решения по амплитуде определялась по среднеквадратичному отклонению амплитуды экспериментальных данных от модельной амплитуды, нормированному на максимальную амплитуду рассеянного на метеорном следе сигнала, согласно выражению

σ A

A,r A (Rk, 10,0) , где σА — среднеквадратичное отклонение экспериментальной амплитуды от модельного значения:

₁        ^Np N s                             ²

^C A =             й        ^(Ф m ⁽ t l ■ n ) - ^{Ф ( R}k , t l ■ n ) ) .

I N p N s - I ) l = 0 n = 0

Ошибка найденного решения по фазе определялась по среднеквадратичному отклонению экспериментальной фазы от модельной:

1         N p N s                               2

°* =( NN : 4 - 2 ^(ф - ^{( t l} , ■ ^{)-Ф( R}k , ^tl ■ n ^{)) .}

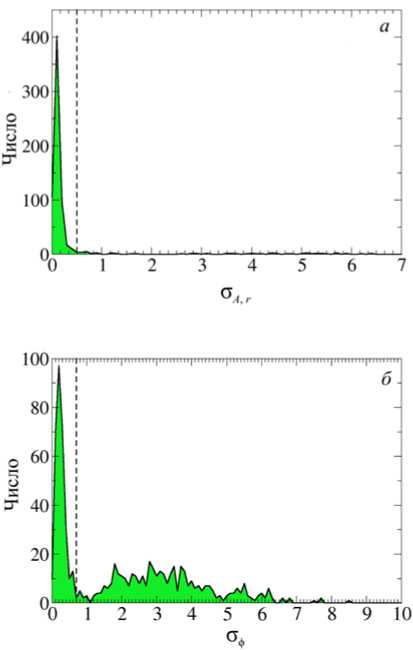
Рис. 3 . Распределения нормированной ошибки найденного решения по амплитуде σ, _r ( а ) и ошибки найденного решения по фазе σ ϕ ( б ). Штриховой линией показаны пороговые значения

Как показал качественный анализ, использование подобных доверительных интервалов позволяет (за счет отсева случаев, когда модель рассеяния на одиночном underdense следе неадекватна экспериментальным данным) дополнительно ограничить область уверенного определения параметров метеорного эха, увеличив степень доверия получаемым данным.

Примеры записей, удовлетворяющих как условиям (1)–(3), так и условию качественного фитиро-вания (9), приведены на рис. 4: a, д и в, ж — амплитуды и фазы сигналов соответственно; б, е и г, з — квадратурные компоненты сигналов. Черными точками на рисунке представлена запись сигнала, используемая для фитирования, окружностями показаны точки, которые отброшены как шум по критерию (4), сплошными линиями показана модель, которая по результатам фитирования имеет мини- мальное отклонение от экспериментальных данных.

Одним из основных геофизических параметров, определяемых по параметрам рассеяния на метеорном следе, является коэффициент диффузии, который можно оценить по характерному времени жизни эха [Jones, Jones, 1990] . В случае underdense эха характерное время жизни следа в первом приближении напрямую связано с коэффициентом диффузии на высоте абляции [Tsutsumi et al., 2009]:

λ ² τ= 32 π ² D ^,

где τ — характерное время жизни; λ — длина волны зондирующего сигнала; D — коэффициент диффузии для данной высоты. Это выражение справедливо в диапазоне высот 85–95 км [Kam et al., 2019] , который мы и будем далее анализировать. В свою очередь, коэффициент диффузии может быть определен следующим образом:

6.39 ⋅ 10 ^{- 2} KT ^{2 p}

где T — абсолютная температура; p — давление; K — подвижность ионов метеорного следа (в подобных задачах обычно принимается как 2.2·10^-4 [м² с^–1 В^–1] [Tsutsumi et al., 2009]).

Высота рассеяния рассчитывается итеративно с помощью модели NRLMSIS-00 с использованием функции расчета параметров атмосферы для заданного времени, координат и высоты. На рис. 5 приведено распределение высот рассеяния для каждого метеорного эха, обнаруженного в период с 1.01.2017 по 20.08.2019. Представленные результаты построены в предположениях, что высота всех регистрируемых метеорных следов связана со временем жизни выражениями (10), (11) и ошибка в определении высоты вызвана исключительно неточностями в определении коэффициента диффузии. Моделирование показало, что ошибка определения коэффициента диффузии ±25 % приводит к ошибке определения высоты порядка ±2 км, что и определяет точность полученных результатов в первом приближении. Однако время жизни некоторых метеорных следов может быть связано с параметрами нейтральной

Monitoring observations of the meteor echo атмосферы более сложным образом — это, например, характерно для метеорных следов промежуточного типа или метеорных следов на высотах выше 95–100 км или ниже 85 км. Поэтому в дальнейшем для дополнительной верификации данных могут быть привлечены другие методы, например, угломестные наблюдения, а также наблюдения за суточной и полусуточной вариациями скорости нейтрального ветра.

Как видно из рис. 5, основная часть распределения находится в коридоре 80–100 км с максимумом в районе 89 км, что согласуется с результатами [Tsutsumi et al., 2009]. Хотя в данных и присутствует обрезание распределения по высоте за счет низкого потенциала радара, однако полученные распределения метеоров позволяют в дальнейшем анализировать данные в высотном коридоре 85–95 км.

Проверка ракурсных характеристик метеорного рассеяния на примере максимумов потоков Геминид (2018 г.) и Персеид ( 2019 г.)

Для проверки правильности интерпретации рассеянного сигнала как рассеяния на метеорном underdense следе была проведена проверка ракурс-ности рассеяния. Согласно существующим представлениям, метеорное эхо во время сильных метеорных потоков характеризуется определенной точкой на небесной сфере — радиантом. Радианты большинства потоков достаточно точно рассчитываются на день максимума потока и публикуются в соответствующих астрономических календарях. Поскольку верхняя часть атмосферы существенно выше высоты абляции метеора, обладает низкой плотностью и слабо влияет на траекторию метеоров, их движение до высоты полного испарения можно рассматривать как прямолинейное с известным направлением, которое может быть рассчитано, исходя из радианта потока. Вытянутость неоднородности вдоль траектории метеора и ракурсные особенности рассеяния на такой вытянутой неоднородности приводят к известной ракурсной зависимости метеорного рассеяния [McKinley, 1961] .

Чтобы убедиться, что выделенные нами сигналы действительно являются сигналами, рассеянными на метеорных следах, было проверено наличие ракурсного эффекта, соответствующего рассеянию на метеорном потоке с известным радиантом. Для проверки алгоритма были выбраны дни 14.12.2018 и 13.08.2019, соответствующие интенсивным метеорным потокам Геминид и Персеид. В результате обработки экспериментальных данных радара EKB ИСЗФ СО РАН было обнаружено за сутки 2100 и 5400 уверенных регистраций метеорного рассеяния соответственно.

Для каждого обнаруженного метеора нами определялось географическое положение точки рассеяния, исходя из измеренного азимута на метеор и дальности до него. Высота рассеяния определялась по характерному времени жизни с помощью модели NRLMSIS-00, как описывалось ранее. В полученной географической точке рассеяния рассчитывался вектор

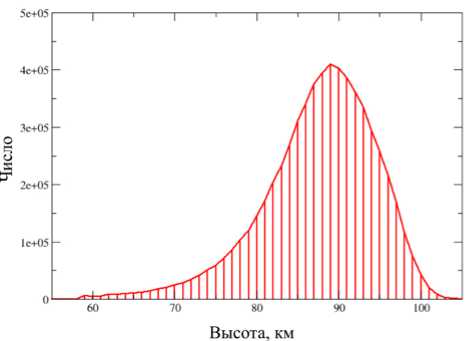
Рис. 5 . Распределение оценки высоты рассеяния, рассчитанной по характерному времени затухания с помощью модели NRLMSIS-00. Наблюдения с 01.01.2017 по 20.08.2019

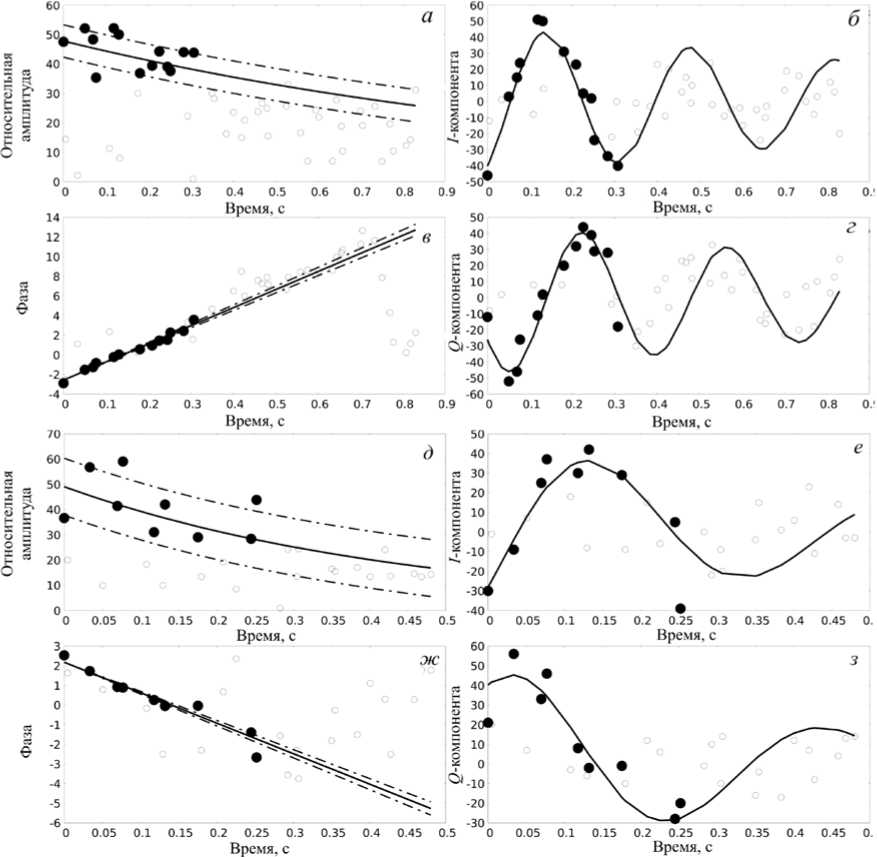
Рис. 4 . Примеры качественно фитированного сигнала метеорного эха: а-г — первый пример; д - з — второй пример; а , д — модуль амплитуды сигнала A(R k , t l , n ); в , ж — фаза сигнала ф( R k , t l , n ); б , г , е , з — квадратурные компоненты сигнала I / Q . Точки — экспериментальный принятый сигнал, окружности соответствуют шумовым измерениям. Сплошные линии соответствуют модельной функции, штрихпунктирные — СКО

направления на радиант метеорного потока и определялся угол между направлением луча зрения на ме- теорный след и вектором направления на радиант. Точность определения направления на след по азимуту составляет от 3° до 6° в зависимости от частоты зондирования. Точность определения направления на след по углу места зависит от точности определения высоты рассеяния и связана с точностью определения характерного времени жизни следа, плотности нейтральной атмосферы, температуры, давления и многих других параметров. При оценках точности определения высоты мы считали, что все эти вариации приводят к ошибке определения коэффициента диффузии не более 20 %. Это соответствует точности определения высоты порядка 2 км и точности по углу места не хуже 0.3°. Нами было проведено моделирование, в результате которого показано, что в переводе на отклонение от перпендикуляра к направлению следа ошибка составляет для Геминид ±2°, а для Персеид ±1°. При расчете направления на метеор учитывалась конусность диаграммы направленности, связанная с линейным расположением антенн [Shepherd, 2017].

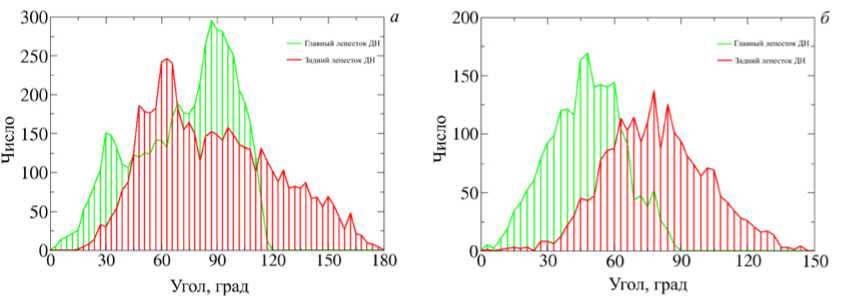
Рис. 6 . Распределения углов между направлением на радиант и направлением на точку рассеяния в предположении рассеяния в главном (зеленый цвет) и заднем (красный цвет ) лепестках диаграммы направленности: a — Геминиды 14.12.2018; б — Персеиды 13.08.2019

Поскольку на момент эксперимента радар EKB не обладал возможностью измерения угла места рассеянного сигнала, а диаграмма направленности (ДН) радара имеет выраженный задний лепесток, существует вероятность, что наблюдение данного метеора происходит в заднем лепестке. Поэтому при оценке ракурсного угла расчеты проводились для случаев нахождения метеоров как в заднем, так и в основном лепестке ДН. На рис. 6, a , б показаны распределения углов между направлением на радиант и направлением на точку рассеяния в предположении рассеяния в основном лепестке (зеленый цвет) и заднем лепестке (красный цвет) ДН радара. На рис. 6, а видно, что рассеяние в основном лепестке ДН обладает существенными ракурсными свойствами — большая часть метеоров наблюдается, когда луч зрения почти перпендикулярен направлению на радиант метеорного потока, однако присутствует второй пик, связанный, вероятно, с рассеянием в заднем лепестке ДН. Исходя из этого, оцениваем распределение по уровню 0.707, что дает ширину 21°. На рис. 6, б представлена картина, соответствующая преимущественному наблюдению метеоров в заднем лепестке ДН, при этом видна существенно большая ширина распределения в области 90°: ширина по уровню 0.707 составляет 33°. Из этого можно сделать предварительный вывод, что рассеяние обладает ракурсными свойствами, характерными для метеорных потоков. Для более детального анализа необходимо задействовать интерферометрические наблюдения на радаре для эффективного разделения рассеяния в переднем и в заднем секторах обзора.

Статистика результатов наблюдений метеорных следов на радаре EKB

На рис. 7 приведена статистика наблюдений метеоров на радаре EKB за период с конца января 2017 г. по август 2019 г. Статистика включает в себя более 6.8 млн наблюдений метеоров, или порядка 260 метеоров в час, что приближается к показателям специализированных установок [Premkumar et al., 2019; Korotyshkin et al., 2019]. На рис. 7, a представлено среднее число эхо-сигналов, обнаруженных алгоритмом, в зависимости от местного звездного вре- мени (LST). Как видно, основной пик приходится на предрассветные часы, минимум приходится на 18– 19 LST. Данное распределение подобно распределениям, полученным с помощью как оптических методов [Lovell, 1954], так и других радиолокационных установок [Thomas et al., 1988]. На рис. 7, б приведено распределение числа метеорных следов по времени жизни. Из рисунка видно, что наиболее вероятное время жизни составляет порядка 0.6–0.7 с. На рис. 7, г приведено распределение числа метеорных следов по доплеровской скорости вдоль луча зрения. Из рисунка видно, что по модулю скорость обычно не превышает 150 м/с, что говорит о том, что пределы поиска нейтральной скорости также выбраны корректно. На рис. 7, в приведено распределение числа метеоров по дальности. Из него видно, что основная часть наблюдений метеорного эха сосредоточена в диапазоне дальностей до 300 км, что соответствует известному ограничению по дальности, используемому при обработке метеорных данных на радарах сети SuperDARN [Jenkins et al., 1998].

Для проверки алгоритма было проведено сравнение расчетных доплеровских скоростей, определенных нашим алгоритмом и стандартным алгоритмом FitACF [Ribeiro et al., 2013] . Сравнение проводилось в точках, определенных новым алгоритмом как метеорное эхо. На рис. 8 представлено сравнительное распределение доплеровских скоростей. Как можно видеть, имеется соответствие между двумя алгоритмами, что позволяет использовать новый алгоритм для определения параметров нейтрального ветра на высотах абляции метеоров.

ОПРЕДЕЛЕНИЕ ПОЛНОГО ВЕКТОРА СКОРОСТИ НЕЙТРАЛЬНОГО ВЕТРА

Как было показано ранее, новый алгоритм позволяет определять характерное время жизни и доплеровскую скорость метеорного следа. Была продемонстрирована также возможность определения высоты рассеяния исходя из характерного времени жизни, что позволяет определить координаты точки рассеяния и положение луча зрения даже при отсутст-

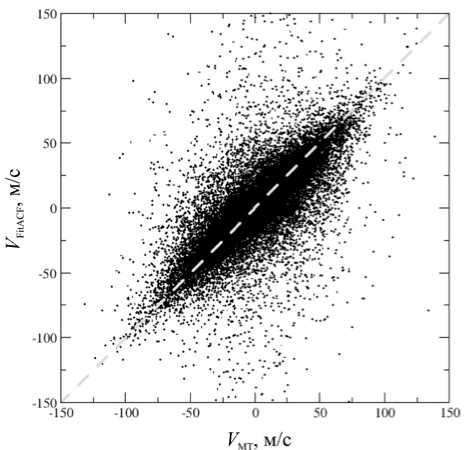
Рис. 8 . Сравнение доплеровских скоростей по результатам работы нового алгоритма и FitACF. Серая штриховая линия соответствует прямой x = у

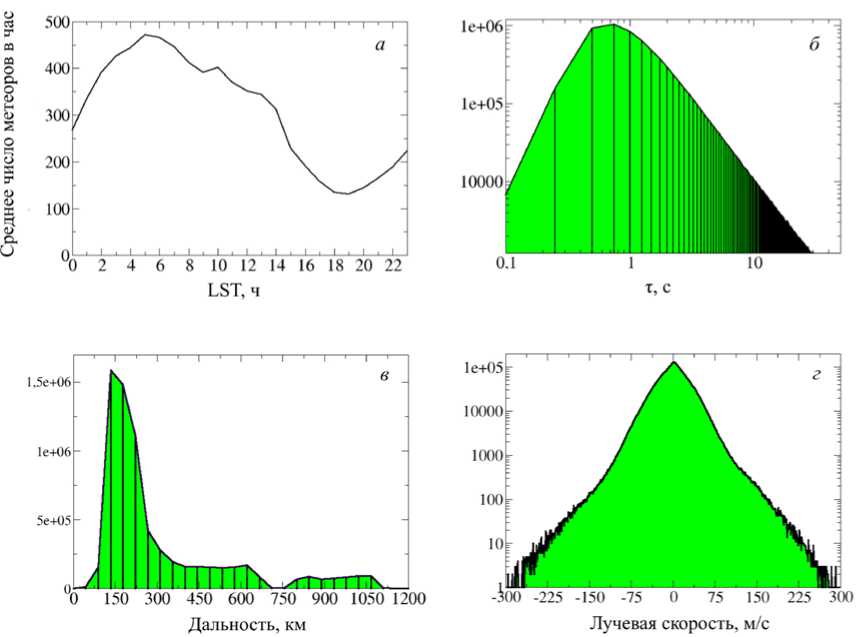
Рис. 7 . Статистика наблюдений метеорного рассеяния на радаре EKB: a — среднее число метеоров в час в зависимости от местного звездного времени; б — распределение характерного времени жизни метеорного следа; в — распределение радиолокационной дальности до следа; г — распределение доплеровской скорости следа вдоль луча зрения

вии интерференционной решетки, как в случае радара EKB до сентября 2019 г. Совокупность этих факторов и то, что сектор обзора радара достаточно широк, дает возможность решить задачу восстановления полного вектора скорости нейтрального ветра в предположении изотропности ветра в секторе обзора. В этом случае можно определить полный вектор скорости нейтрального ветра в рамках взвешенного метода наименьших квадратов.

При этом средний ветер определяется по экспериментальным данным, исходя из условия минимума функционала взвешенной квадратичной невязки:

^ (V x , V y , V z ) = S { W ( R i )V , i + V x k x ,i + i                                      (12)

+ V y k y,i + V z k z , i ⁾² } = min.

Здесь V d , i — измеренная скорость вдоль луча зрения; V x , V y , V_z — проекции нейтрального ветра в локальной для точки рассеяния i -го метеора горизонтальной системе координат, локально параллельной земной поверхности в приближении сферической Земли (ось X направлена на север, ось Y направлена на запад, ось Z направлена вертикально вверх); k_x , i , k y , i , k z , i — компоненты единичного вектора в направлении луча зрения на эхо, пересчитанные в его локальную систему координат; R i — дальность от радара до рассеивающего метеорного следа; i — порядковый номер метеора в исследуемый временной период; W ( R i ) — весовая функция. Введение веса необходимо из-за значительной (до 45 км) длительности зондирующего импульса, что дает большую погрешность в определении положения луча зрения в пространстве на малых (<300 км) дальностях, а следовательно, значительную погрешность при расчете горизонтальных компонент вектора скорости. Как видно из рис. 7, в , таких метеорных следов большинство.

Задача определения компонент вектора по методу (12) является простой аналитической задачей, сво- дящейся к решению системы трех линейных уравнений на Vx, Vy, Vz. Единственной проблемой, требующей решения, является корректное определение весовой функции W(Ri).

Согласно принципам взвешенного метода наименьших квадратов, при нормальном распределении ошибок весовая функция W ( R_i ) обратно пропорциональна дисперсии соответствующего элемента суммы:

W ( R i ) = o Д R i ). (13)

Таким образом, для определения веса W(Ri) необходимо оценить дисперсию скорости как функцию расстояния до метеора. В данном случае при определении компонент вектора скорости случайным параметром остается угол места α(R, h0), однозначно определяемый по дальности R и высоте рассеяния h0. При этом мы полагаем распространение радиосигнала прямолинейным. Рефракцией, особенно на малых дальностях и сравнительно высоких углах места, в первом приближении можно пренебречь, поскольку плазменная частота ионосферы на этих высотах обычно достаточно низка — существенно ниже рабочей частоты зондирования. Параметром, влияющим на дальность, является пространственное разрешение δr, дающее равномерное распределение возможной дальности до следа в пределах от R до R+δr. Таким образом, мы получаем равномерное распределение для a = a cos

R E + R ² - ( R e + h о ^{) 2}

2 RR

V            ^E 7

в пределах от α( R , h ₀) до α( R +δ r , h ₀), где R _E — радиус Земли. Поскольку компоненты вектора луча зрения находятся в прямой зависимости от значения угла места, то дисперсия скорости пропорциональна дисперсии угла места. Тогда вес каждой точки можно определить следующим образом:

W ( R ) =

( a ( R , h 0 ) -a ( R + 8 r , h 0 ) ) 2 ^.

Выражение (15) и нужно использовать при расчете скорости нейтрального ветра взвешенным методом наименьших квадратов (12).

Верификация метода восстановления скорости нейтрального ветра

Для проверки метода мы сверяли полученные данные с моделью горизонтального нейтрального ветра HWM-14. Наблюдения с 01.01.2017 по 20.08.2019 показали среднее число 260 метеоров в час. Для анализа использовались данные для различных времен года. Наблюдения разбивались на временные интервалы длительностью 1 ч, по которым определялся полный вектор скорости ветра. Полученные значения горизонтальных компонент усреднялись в пределах изучаемого часа за весь период наблюдений. Таким же образом усреднялись значения компонент вектора скорости, полученные по модели HWM-14. В качестве примера на рис. 9 представлен результат наблюдений в период с 8 по 25 января 2017 г. в высотном коридоре 85–95 км.

На панелях a и б представлены расчетные (черная линия) и модельные (серая линия) меридиональная и зональная компоненты скорости горизонтального ветра, на панелях в и г — СКО меридиональной и зональной компонент скорости ветра (серая линия) и распределение среднего числа метеоров в час (штрихпунктирная линия), на панелях д и е — сравнение скоростей ветра, рассчитанных в трехмерной (черная линия) и двумерной (серая линия) моделях. На панели ж представлено распределение вертикальной скорости согласно трехмерному расчету.

Как видно из рис. 9, расчетные значения компонент скорости ветра качественно соответствуют модельным. В области суточного минимума числа наблюдаемых метеоров наблюдается значительный рост СКО (25–60 м/с) расчетной скорости. Видно также большое СКО (15–20 м/с) расчетной скорости, возможно связанное с тем, что все расчеты ведутся в предположении рассеяния только в переднем лепестке, без использования угломестных измерений.

В рамках тестирования этого алгоритма был обнаружен большой разброс расчетной вертикальной компоненты (СКО 40 м/с), что ожидаемо в рамках эксперимента ввиду малых наблюдаемых углов места. В то же время математическое ожидание расчетной вертикальной компоненты было близко к нулю, что согласуется с известным фактом малой вертикальной скорости ветра в этой области. Поэтому был проведен тот же самый расчет без учета вертикальной компоненты (т. е. двумерный расчет), показавший в среднем близкие результаты 2-мерного и 3-мерного расчетов скорости горизонтального ветра, что объясняется малостью средней вертикальной скорости.

ЗАКЛЮЧЕНИЕ

В работе рассматривается реализация алгоритмов автоматического поиска по данным радара EKB ИСЗФ СО РАН сигналов, рассеянных на метеорных следах. Алгоритм включает два этапа: 1) обнаружение метеорного эха; 2) определение его параметров. На первом этапе ищутся пространственно-локализованные всплески амплитуды над средним уровнем сигнала, монотонно спадающие во времени. На втором этапе методом наименьших квадратов амплитудная и фазовая развертки сигнала аппроксимируются экспоненциальной моделью амплитуды и линейной моделью фазы и проводится дополнительная фильтрация найденных метеорных следов по результирующей точности аппроксимации фазы и амплитуды. В целом алгоритм аналогичен алгоритмам, применяемым на специализированных метеорных установках [Tsutsumi et al., 1999] , однако учитывает аппаратно-программные особенности радара EKB.

При тестировании алгоритма было показано, что в дни максимумов потоков Геминид 14.12.2019 и Персеид 13.08.2019 детектируемые алгоритмом рассеянные сигналы носят ракурсный характер (см. рис. 6, а и б ). В случае Геминид ракурсное рассеяние соответствует предположению, что метеорные следы наблю-

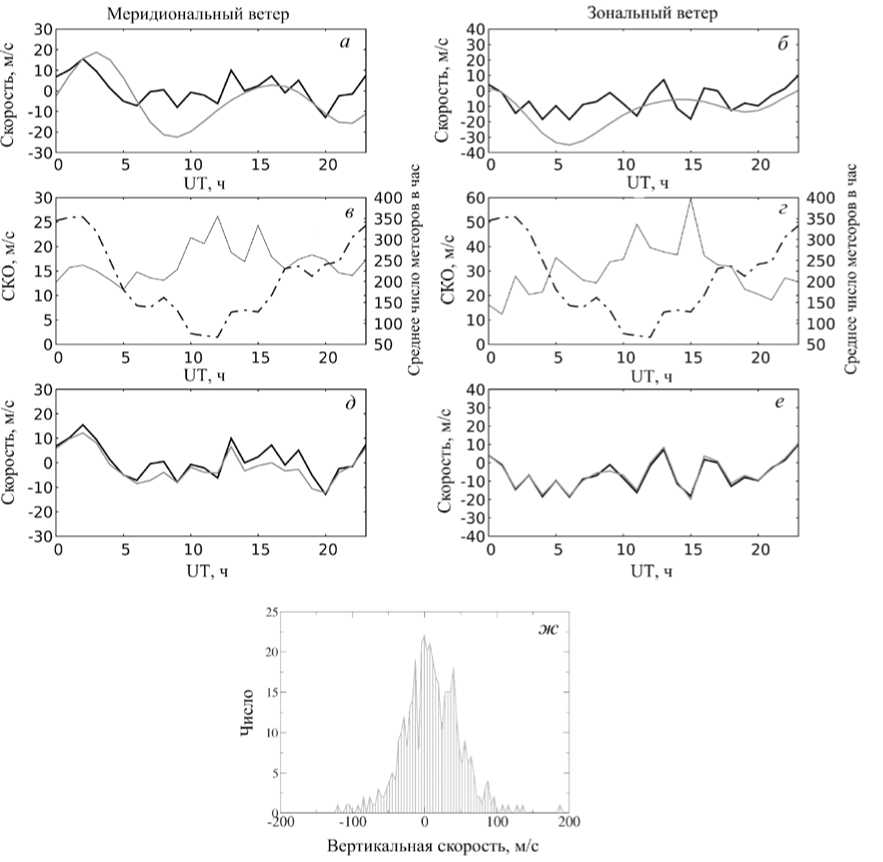
Рис. 9 . Сравнение результатов, полученных по модели HWM-14 и в ходе эксперимента в высотном коридоре 85–95 км: а и б — меридиональная и зональная компоненты скорости ветра (положительные значения соответствуют движению на север и запад соответственно), усредненные по высотам (85–95 км) и времени, черные линии — эксперимент, серые линии — модель HWM-14; в и г — СКО расчетных значений меридиональной и зональной компонент скорости (серые линии) и среднее число метеоров в час (штрихпунктирная линия); д и е — сравнение двумерного и трехмерного расчетов: черная линия — 3D, серая — 2D; ж — распределение вертикальных скоростей для трехмерного расчета. Наблюдения с 08.01.2017 по 25.01.2017

даются преимущественно в главном лепестке ДН, а ширина распределения по уровню 0.707 составляет порядка 21°. В случае Персеид ракурсное рассеяние соответствует предположению, что метеоры наблюдаются преимущественно в заднем лепестке ДН, ширина распределения по уровню 0.707 составляет порядка 33°. Разделение главного и заднего лепестка по данным радара в рассматриваемый период провести нельзя из-за отсутствия дополнительных антенн в составе решетки. Это подтверждает, что источником выделяемых алгоритмом сигналов с высокой степенью вероятности является рассеяние на метеорных следах. Было также проведено сравнение расчетных доплеровских скоростей, определяемых нашим алгоритмом и стандартным алгоритмом FitACF (используемым на радарах SuperDARN для расчетов продольной скорости [Ribeiro et al.,

2013] ). Сравнение показало в среднем хорошее соответствие продольных скоростей, получаемых этими методами.

В работе приведено решение обратной задачи восстановления вектора скорости нейтрального ветра по полученным данным взвешенным методом наименьших квадратов в рамках предположения об изотропности поля нейтральных скоростей в локальной системе координат метеора. На основе геометрических соображений определена весовая функция метода и реализован алгоритм определения полного вектора скорости нейтрального ветра в рамках описанных предположений.

Для тестирования метода решения обратной задачи восстановления полного вектора скорости нейтрального ветра на базе долговременных измерений метеорного эха (с 1.01.2017 по 20.08.2019)

проведено восстановление скорости и направления нейтральных ветров в моделях двумерного (горизонтального) и трехмерного ветра. Проведено сравнение полученных данных с моделью горизонтального ветра HWM-2014. Расчетная схема скорости и направления ветра (2D или 3D) существенно не влияет на среднесуточный ход ветров. Для более детального сравнения требуется анализ данных дополнительной (интерференционной) антенной решетки, запущенной в эксплуатацию лишь недавно, для разделения рассеяния в переднем и заднем лепестках ДН.

Описанный в работе алгоритм выделения сигналов, рассеянных на метеорных следах, и определения параметров этих cледов: продольной доплеровской скорости и времени жизни — введен в постоянную эксплуатацию на радаре EKB ИСЗФ СО РАН.

При получении результатов использованы данные радара EKB ИСЗФ СО РАН. Результаты получены с использованием оборудования Центра коллективного пользования «Ангара» []. Работа выполнена при финансовой поддержке Минобрнауки России.