Monkey behavior based algorithms - a survey

Published Online December 2017 in MECS

There are numerous real-time NP-hard problems that can be solved optimally with the help of various optimization techniques. Even though NP-hard problems cannot have exact solutions, stochastic optimization techniques help in finding the optimal solutions in various fields. For solving optimization problems, nature-inspired algorithms such as evolutionary algorithms, evolutionary programming and swarm intelligence algorithms are used in diverse fields such as medicine, engineering, chemistry, physics, and economics. Swarm intelligence is based on the intelligent behavior and adaptation of various animals, birds, and insects and is considered as a level next to that of human intelligence.

Swarm intelligence mimics the intelligence and the problem-solving techniques followed by the animals, birds, etc, and are also called as bio-inspired algorithms.

Examples of Swarm intelligence algorithms are Particle swarm optimization (PSO), Ant colony optimization (ACO) both being the front-liners, also include Artificial bee colony (ABC), Krill herd algorithm (KHA), fruit fly algorithm, Firefly algorithm etc. One of the interesting algorithms in this group is Monkey search optimization algorithm [1]. In this survey, various Monkey search algorithms and their applications are reviewed. Monkey search is inspired by the climbing habit of monkeys over the trees. Later a variation of monkey algorithm [2] was proposed simulating the mountain climbing behavior of monkeys. Spider monkey optimization was proposed by J.C. Bansal [3] based on the Spider monkey’s behavior for searching the food.

The rest of the paper is organized as follows: Section 2 briefs about swarm intelligence algorithms and Section 3 provides a general overview of all the Monkey behavior based algorithms. Section 4 deals with different types of monkey search algorithms and their applications; Section 5 describes monkey algorithms and their applications. Section 6 describes the hybrid of MS and MA algorithms with applications; Section 7 describes Spider monkey optimization algorithms, their types together with their applications and Section 8 compares and summarizes monkey behavior based algorithms; Finally, Section 9 concludes the survey and provides future directions in this field.

• II.    Swarm Intelligence Algorithms

Mathematical optimization is considered as choosing the superior item/thing from the set of alternative items/things within a specific domain based upon some criteria. Optimization algorithms can be divided into two types: exact and heuristics [4]. Exact algorithms arrive at the optimal solution in a finite time interval and there is an assurance for the solution. In the case of heuristic algorithms, the optimal solution is not always guaranteed, but it can cover a huge search space. But properly designed heuristics can be helpful in solving the real-life optimization problems which are NP-hard problems as well.

The problems are of two types, deterministic and stochastic. Deterministic problems can be solved in real time with the given predefined input and the initial conditions following a certain predefined steps to give rise to a single perfect solution. Stochastic problems cannot be solved in a specific time as it is determined by several random parameters including the input values. Most of the real-world optimization problems are stochastic in nature and will give rise to different solutions under the same/different circumstances for the same/different set of inputs. A metaheuristic is the heuristic about heuristic and is always problem independent, whereas heuristics are problem-dependent. Combinatorial optimization problems follow metaheuristic methods. They use random inputs along with constraints that need to be satisfied while solving the problem. They may arrive at a number of feasible solutions instead of a single optimal solution.

There are several algorithmic techniques to solve complex combinatorial optimization problems varying from evolutionary computation to swarm intelligence algorithms. In general, the meta-heuristics algorithms are based on either the natural phenomenon or the organism’s behaviors. Natural phenomenon includes the Tabu search, simulated annealing, Gravitational force [5], Water drops, etc. Algorithms based on organisms’ behaviors include Bacterial behavior, Ant behavior [6], Bee behavior, Bird behavior, Whale behavior, firefly behavior [7] and the recent Grey wolf behavior and monkey behavior.

Bonabeau defined swarm intelligence as "any attempt to design algorithms or distributed problem-solving devices inspired by the collective behavior of social insect colonies and other animal societies" [8]. Karaboga et al. mentioned [9] as "Division of labor and Selforganization are the important and sufficient conditions for getting the intelligent swarming behaviors. Social organisms learn, share and adapt to the changing environment to solve complex tasks". A lot of study and analysis were done over the social behaviors. Researchers have designed many swarm intelligence algorithms which can be applied to solve nonlinear and combinatorial optimization problems in various domains.

• III.    Monkey Behavior based Algorithms

In this survey, the monkey behavior based algorithms are categorized into four types as shown in Fig. 1. Monkey search algorithm is simulated based on the behavior of monkeys climbing up the trees. Monkey algorithm is based on the monkeys climbing over the mountains. Hybrid of Monkey search and Monkey algorithm combines the features of both the algorithms and finally an optimization algorithm based on the Spider monkey food searching behavior has evolved. These categories are discussed in detail in the subsections below.

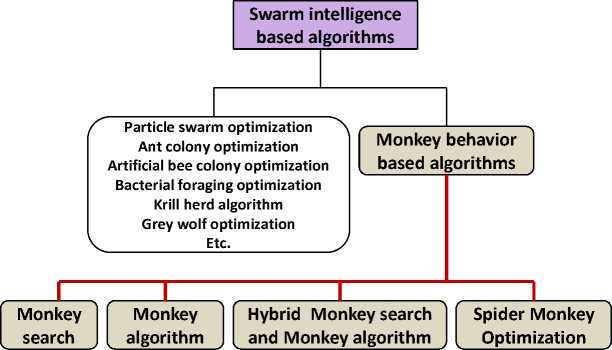
Fig.1. Categorization of Monkey behavior based algorithms

• A.    Monkey search algorithm

Monkey search algorithm is an agent-based algorithm where the agent imitates the behavior of the monkey. It mainly focuses on the activities of a monkey climbing on the tree in search of food as shown in Fig. 2. In the Monkey search (MS) algorithm [1], it is assumed that the monkey explores the trees and learns the exact paths that lead to better food. The tree over which the monkey climbs is considered to have solutions to the optimization problem, and its branches represent perturbations which can transform one solution into another. With the help of random mechanism, at each step, the monkey chooses the branches. This random mechanism is based on the objective function values of the new solutions. The monkey prefers better solutions, but it is up to the monkey to choose the solutions. Each and every time a monkey finds better solution, it returns to the root and stores it as a current best solution in the memory. The monkey climbs up the tree again targeting the branches with better values. The binary tree data structure is used for this monkey search. The trees over which the monkey climbs are assumed to have two branches i.e. a left and a right branch. The Binary tree data structure consists of:

• •    A set of nodes connected by paths, and “A” is the first node called root.

• •    The root and nodes are considered to have food sources which correspond to the probable solutions of the problem to be optimized.

• •    Each branch is linked with the current solutions’ perturbation. The branches allow the monkeys to climb the tree from one node to another indicating the transition from one solution to another.

• •    The adaptive memory is maintained to store the information obtained during the scan process in the solution space and this is referred in the rest of the search process. This structure is shown in Fig. 3.

Fig.2. Monkey climbing up a tree

Fig.3. The tree structure of the MS algorithm

In the binary tree structure, two different perturbations are applied. The monkey search algorithm was proposed as a general framework where the features of other optimization algorithms such as Genetic Algorithm [10], Ant colony optimization [11], Harmony search [12] etc., can be included in it. When all the values stored in the memory are almost close, the Monkey search algorithm achieves the convergence globally. Fig. 4 shows the types of monkey search algorithm.

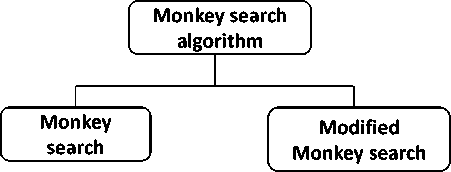
Fig.4. Types of Monkey search algorithm

The monkey search algorithm is dependent on the following parameters for its convergence:

• 1.    Height of the trees

• 2.    Number of times the monkey goes to the top of the tree

• 3.  The memory size

• 4.  Initial number of random trees

The termination condition for the monkey search algorithm is arrived when the difference between the objective function values of all the solutions stored in the memory is less than the threshold value.

• B.    Monkey algorithm

Monkey algorithm [2] is influenced by the mountain climbing behavior to solve optimization of multivariate systems. Fig. 5 shows the monkey’s mountain climbing behaviors and its processes in monkey algorithm. It is assumed that in the field there are several mountains, which denote the feasible search space of the problem. This algorithm was designed with three processes such as climb process, watch-jump process, and somersault process. The details of the three processes of MA are discussed below:

• 1.    Climb process

• 2.    Watch-Jump process

• 3.    Somersault process

When the monkeys climb over the mountain, they climb carefully step-by-step. This climbing behavior is modeled as the climb process in the monkey algorithm to locate optimal solution in the local search space as per the pseudo-gradient information of the objective function. The parameter in the climb process called ‘Step length’ can be defined to control the step size of the monkeys.

To reach the mountain-top, the monkeys climb up the mountain. They will watch around the local peak position. The parameter of watch-jump process called ‘Eyesight’ parameter can be used to define the maximum distance or the range that the monkey can watch. If any nearby higher mountain is seen compared to that of the current position, it will jump to that position and try to climb up. This process is actually modeled in the watch-jump process to expedite the search. The obtained current solution is modified with the new and improved solution.

The monkeys will usually somersault to the new area to explore them. In this process, the barycenter from the current positions of all the monkeys are selected which is termed as the pivot. The monkeys will somersault to a new position either to or fro with respect to the pivot point. The parameter of somersault process called ‘Somersault interval’ can be used to govern the maximum distance that the monkey can somersault. This process makes sure that there are new solutions in the globally fresh search space.

Fig.5. Monkeys on Mountain as in Monkey algorithm

When each monkey reaches the mountain top, it will take some rest to find out whether there are any other mountains nearby which are higher than the current positions. After watching from the current position, the monkey will jump to an adjacent mountain in watch-jump process followed by the consecutive climbing processes till the mountain top is reached for each monkey. Fig. 6 shows the types of the monkey algorithm discussed in this review.

Monkey algorithm

Monkey algorithm (MA)

DMA (Discrete monkey algorithm)

MMA (Modified monkey algorithm)

DAMA (Monkey algorithm with dynamic adaptation)

AMA (Adaptive monkey algorithm)

IMA (Immune monkey algorithm)

NMA (Niching monkey algorithm)

ABC-MA (Monkey algorithm with ABC search operator)

TAMA (Triaxial accelarometer monkey algorithm)

Improved monkey algorithm

MAKHA (MA and Krill Herd algorithm)

Fig.6. Types of Monkey algorithm

CMA (Chaotic monkey algorithm)

To find a comparatively higher mountaintop, the monkeys will follow the somersault process to an entirely new search domain along the direction pointed towards the pivot. After a predefined number of cycles of these processes, the highest mountaintop discovered by the monkeys is considered as the optimal solution. Monkey algorithm is considered to solve non-linear, multidimensional and multimodal optimization problems.

The steps involved in the MA are given below:

• 1.    Population Initialization

• 2.    Individual monkeys climbing process.

• 3.    Watch-Jump process with watch process for finding comparatively higher mountain tops and jump process for jumping to that mountain and repeat the climb process till the mountain top is reached.

• 4.    Somersault process is carried over to explore new mountain tops.

• 5.    Check for the termination criteria with the help of predefined cycle number.

If termination condition is not satisfied then go to the step 2 and repeat again. Otherwise, display the optimal solution and objective values.

• C.    Hybrid of MS and MA algorithms

The Monkey search and the monkey algorithms are combined to give rise to hybrid MS and MA algorithms. This hybrid algorithm combines the monkey tree climbing behavior and the perturbation operators of monkey search with the monkey mountain climbing behavior along with the three processes, namely climb, watch-jump and somersault to yield better outcomes. The

Fig. 7 shows the types of the hybrid MS and MA algorithms.

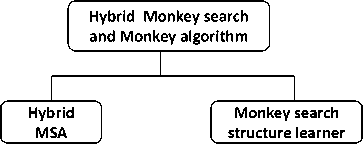
Fig.7. Types of hybrid MS and MA

• D.    Spider monkey optimization

Spider monkey optimization (SMO) [3] is a new swarm intelligent algorithm. This is based on the intelligent foraging behavior of spider monkeys.

Spider monkeys are considered as fission-fusion social animals as they form small groups among themselves from large one and then combine together to form larger groups depending upon the scarcity or the availability of the food. SMO is considered to handle the premature convergence and stagnation efficiently and could result in better solution. Fig. 8 shows the types of modified algorithms of SMO.

The Characteristics of Spider monkeys are as follows:

Spider Monkey Optimization (SMO)

TS-SMO (Tournament selection based SMO)

QASMO (QA based SMO)

Fig.8. Types of Spider Monkey optimization

• •   40-50 spider monkeys form a group.

• •    There is a global leader who is the oldest female member in the group. It will take almost all the decisions within the group.

• •    For efficient food search, several small groups (3 to 8 members) emerge from a single large group.

• •    Each of these subgroups will have a local female leader to monitor the foraging itinerary.

Spider monkeys’ food foraging steps are given below:

• ■    When the food search process starts, the distance from the food sources are computed by the spider monkeys.

• ■    Depending upon this distance the spider monkeys of the group update the positions and compute the

distance again.

• ■    The local leader’s best position is modernized within the group. When it is not done for a particular number of iterations, then that group members divert the search for food sources in various directions.

• ■    At last, the global leader of the largest group maintains its best position. When stagnation occurs the global leader creates subgroups.

SMO follows a trial and error based iterative process. There are six phases in the SMO process. The idea of position update in Global leader phase is obtained from the G-best guided ABC and modified ABC. There are four control parameters defined in SMO. They are global leader limit, local leader limit, maximum group, and perturbation rate.

The Steps in SMO are as follows:

• 1.    Population initialization:  A spider monkey

• 2.    Local leader phase (LLP): In the LLP, the spider monkeys modify their current position from the experience of the local leader and group members. The fitness values of the new position of the monkeys are calculated. Spider monkeys update the old position with the new one when it attains a new higher fitness value. In LLP, the search space is explored, as the group members update their positions. There is a high perturbation in the initial iterations and later reduces gradually.

• 3.    Global leader phase (GLP): In this phase, all the spider monkeys modify their position with the help of the experience of global leader and local group members. This phase improves the exploitation as best fit candidates get better chances to update. A randomly selected dimension is updated in the position update process.

• 4.    Global leader learning (GLL) phase: In GLL phase, the global leader is updated with the position of the best fit spider monkey through greedy selection. When the position of the global leader is not updated, the parameter GlobalLimitCount is increased by one.

• 5.    Local leader learning (LLL) phase: In LLL phase, with the help of greedy selection the local leader is updated with the position of the best fit spider monkey in that local group. Then, the updated position of the local leader is compared with the old one. LocalLimitCount is incremented by one when local leader is not updated.

• 6.    Local leader decision (LLD) phase: When the local leader position update to LocalLeaderLimit is not done, then the group members update their own positions by random initialization or utilizing the Global and local leader information with the help of perturbation rate.

• 7.    Global leader decision (GLD) phase: In this phase, the update to the global leader position is monitored for a particular number of iterations called GlobalLeaderLimit. Then the population is divided into smaller groups

population of size N is generated initially where each monkey is represented by a D-dimensional vector where D denotes the number of problem variables to be optimized.

starting from two to a maximum number of groups by the global leader.

In the GLD phase, LLL processes are started in the newly formed groups to elect the local leader. When the maximum groups are formed and the position of global leader is not updated, then the global leader combines all the smaller groups into a single larger group based upon the inspiration from fusion-fission structure of spider monkeys.

• IV. Monkey Search Algorithms

Monkey search algorithm is modeled by the tree climbing behavior of the monkeys in order to find good food. The algorithm variations are monkey search and modified monkey search algorithms. These algorithms and their applications are shown in Fig. 9.

• A.    Monkey search - Type 1

Monkey search (type 1) [1] is an agent based algorithm where the searching agent exhibits the behavior of the monkey climbing up the trees to search for good food. The tree branches over which the monkeys climb has better solutions to the optimization problem. When the monkey reaches the top of the tree, it stops climbing, which forms the depth of the binary tree structure. The random perturbation determines the functional distance between the two solutions. New feasible solutions are created with the help of the current solution and the randomized perturbation function is used to increase the success percentage of the solution. To avoid the predominance of the specific perturbation function, the choice of perturbation is reset to uniform.

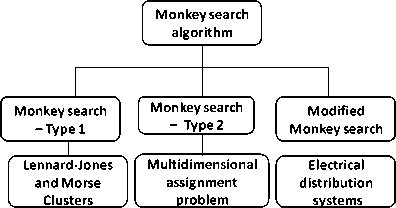
Fig.9. Monkey search algorithm applications

The solutions available in monkey search are the current and the best solution. The list of perturbations applied to the monkey search algorithm are given below:

• 1.    Random changes to the current solution as in simulated annealing method.

• 2.    Crossover operation between the parents (current and the best solution) to generate the children as in Genetic algorithm

• 3.    The mean of the current and the best solutions as in the ant colony optimization.

• 4.    Directions from current to the best solution as in Directional Evolution.

• 5.    Harmonies i.e. solutions for current and best and

introducing random notes as in Harmony search algorithm.

To avoid local optima in Monkey search, a predefined number of the best solutions are updated by each tree into the memory of monkey search algorithm. The search in different spaces is improved by starting the search with a predefined number of trees with randomly generated solutions as root. Whenever a new improved solution arrives, the memory is updated with that new solution and the corresponding least feasible solution is removed from the memory. The branches with better values are preferred to converge to a specific area of the tree where the global solution may exist. The Monkey search is implemented in C Language and applied to the problem of finding Lennard-Jones [13] and Morse clusters [14], as well as for solving the distance geometry problem.

• B.    Monkey search - Type 2

In the Monkey search (type 2) [15], initially, the monkey is considered to be at the root of the tree and the branches have to be slowly created. The current solution is updated whenever the monkey climbs up the tree. After finding the food at the top of the tree, the monkey marks that path as the best solution when it gets down. This is put in the memory whenever the monkey climbs different trees. This monkey search algorithm has its own parameters to set. The height of the tree indicates the number of branches of the tree. The memory size is another parameter for the number of trees that the monkey climbs from the random solution. Predetermined number of best solutions has two parameters. The monkey search algorithm is terminated when all the best solutions in the memory are almost close to one another. To determine the closeness, a cardinality parameter is defined. Small cardinality will stop the method in local minima and high cardinality may eventually increase the computational complexity. In adjusting this cardinality, perturbation plays a lead role in the monkey search algorithm.

The monkey search algorithm has been used to solve the multi-dimensional assignment problem (MAP) [16] which is considered as the generalization of linear dimension problem and also a combinatorial optimization problem.

• C.    Modified Monkey search

In Modified Monkey Search (MMS) [17] optimization, the Monkey search optimization technique [1] is modified with a better representation of the problem. Modified monkey search is inspired by the behavior of a monkey searching for food in a jungle. The initial tree with solutions are obtained from a search process with the help of the perturbations performed on each and every node in the tree. The depth of a tree is obtained by subtracting one from the number of levels. There are two choices for depth in MMS. They are the ‘elevated h’ or the greater depth of the tree and the ‘low h’ value or the lower depth of the tree. Initial tree is converged when all the paths are covered. The adaptive memory has a list of the ten best solutions. These solutions are obtained during the initial tree search and updated from the search in the subsequent trees. The MMS algorithm search process has two steps:

• •    The full search in the initial tree with all candidate paths and solutions in adaptive memory helps to find the subsequent trees.

• •    Second is the directed search in subsequent trees with the help of reference memory.

The method used to modify the optimal solution is the perturbation mechanism. The convergence criterion applies to the initial and the subsequent trees and is different for both the trees. When predefined perturbations are over, the intensification process takes the search process towards these paths. The global convergence in MMS is possible when either:

• •    The difference between the objective functions of the last and first positions of the adaptive memory is less than or equal to a tolerance value.

• •    Or a maximum number of trees are covered.

Steps involved in the MMS algorithm are:

• 1.    MMS parameters are defined and the distribution system data are obtained

• 2.    The Initial tree is explored from the root and is perturbed till the top is reached

• 3.    The better solutions are stored in adaptive memory in descending order

• 4.    Perturbation of the first element is started

• 5.    The better fitness node from step 4 is chosen

• 6.    The new solution from step 5 is evaluated with two situations

• a.    If this new solution is fitter than the current best solution, it is replaced and the new tree is explored from step 4

• b.    Else, the adaptive memory is updated and the control goes to step 7

• 7.    Global convergence is assessed. The algorithm is terminated once the termination condition is fulfilled. Otherwise, the control goes to the next step

• 8.    Verify whether the top of the tree is reached

• 9.    The perturbation generates two new solutions to the new current solution. From this generation, the algorithm goes to Step 5.

MMS is a bio-inspired technique presented for capacitor allocation in distribution systems. The mathematical optimization problem associated with the allocation of capacitor banks is to minimize the energy loss and the investment cost in distribution systems.

• V. Monkey Algorithm

Monkey algorithm is based on the mountain climbing behavior of the monkeys in search of good food in various domains, The variations existing in Monkey algorithm include MA with dynamic adaptation, discrete monkey algorithm, modified monkey algorithm, adaptive monkey algorithm, immune monkey algorithm, niching monkey algorithm, monkey search with ABC operator, triaxial accelerometer monkey algorithm, improved monkey algorithm, monkey algorithm with KHA and chaotic monkey algorithm. These algorithms with their corresponding applications are shown in Fig. 10.

• A.    Monkey algorithm for numerical optimization

  Monkey algorithm (MA) [2] influenced by the mountain-climbing behavior of monkeys was designed by Zhao and Tang, who used continuous variables to solve global numerical optimization problems. This new Monkey algorithm was designed with three processes such as climb process, watch-jump process, and somersault process. After performing these three processes iteratively for a given cycle number N, monkeys will try to find the highest position which is considered as the optimal solution. The position obtained in the last iteration may not be the best. Hence the best one should be saved from the beginning. When the monkeys find a better position, the old one will be replaced by it. After the last iteration, this will be provided as the optimal solution. Monkey algorithm can find the global optimal solution in different domains of search space. This algorithm has been applied to the 12 benchmark problems with dimensions of 30, 1000 or 10000.

• B.    Discrete Monkey algorithm

Discrete monkey algorithm (DMA) [18] is designed with the discrete variables with improved computational capability. There are two types of climb processes introduced in DMA to maintain order in the climb direction of MA namely, Large-step climb process and the Small-step climb process. Monkeys arrive at their corresponding good positions after performing these two climb processes. In the watch-jump process, once they find the higher mountaintops, they jump to that new position and continue climbing. In this process, a parameter called ‘eye shot’ of the monkey is used. In DMA, Cooperation process is proposed to bring in better solutions. Cooperation process among monkeys in the higher and better positions will help the monkeys in the poor positions to come up with the better positions.

The cooperation process improves the diversity and interaction among the population and enhances the search process. To introduce the monkeys into the new search domains, somersault process is used as in original MA with the somersault interval. To make the somersault process more efficient the stochastic perturbation mechanism is proposed in DMA. In this perturbation mechanism, a randomly generated uniformly distributed integer is used. The DMA iterations are terminated when the optimal value remains the same for a K number of generations which is dependent on the nature of the problem. DMA was applied for the Transmission network expansion planning (TNEP) [19] especially for Multidimensional mixed integer static TNEP (STNEP), a discrete optimization problem. Solutions of STNEP are mapped to the position of the monkeys in DMA. Each component of monkey’s position has values varying from zero to the allowed maximum number of circuits. The objective function is to find the transmission expansion scheme or building new transmission facilities with minimum investment and satisfying constraints such as power balance in each node, line flow limits and with the limited decision variables. DMA was tested on two transmission network expansion planning problems having different dimensions such as 18-bus system and IEEE 24-bus system.

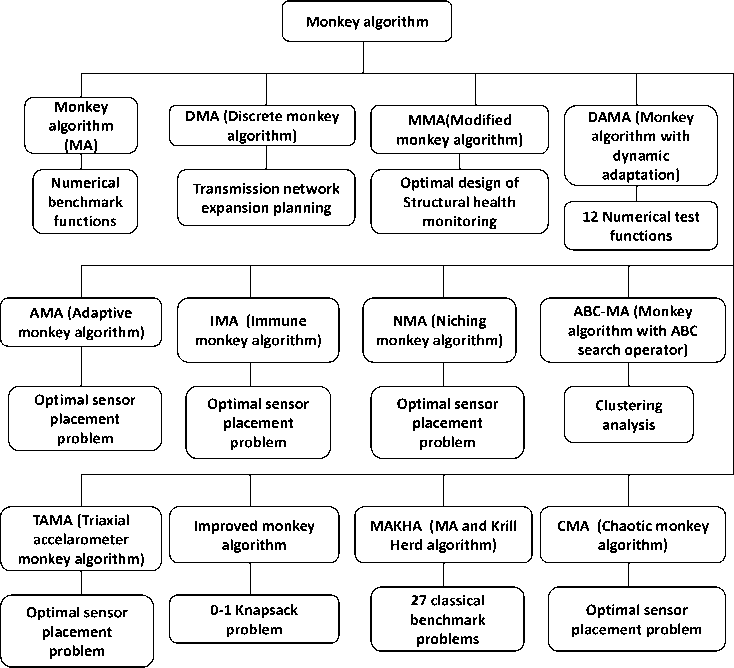
Fig.10. Monkey algorithm applications

• C.    Modified Monkey algorithm

Modified monkey algorithm (MMA) [20] is the improvement of the original Monkey algorithm. As binary coding method of original MA needs increased string length and computational time, MMA uses integer coding method. Population initialization is done by Euclidian distance in MMA as it will increase the diversity of the monkey’s position with a proposed threshold limit instead of random initialization of original MA. When the Euclidian distance is small between the monkey’s positions, the global search ability is reduced. Hence the Euclidian distance is fixed to be greater than or equal to the threshold value. If not, re-initialization should take place to improve the diversity which in turn increases the global search capability. Another change in the MMA is the large step and small step climb processes to avoid the disordered search direction of primary [18] MA in solving discrete optimization problems. The large-step climb process makes the monkeys’ positions to change greatly and also the search range for potential solution will expand. The larger pace in the climbing seems to skip the global optimal solution which in turn needs a greater number of iterations to arrive at the optimal solutions. Therefore, the pitch adjusting rate (par) in the Harmony search algorithm (HSA) [21] is adapted to the new components after the large-step climb process. During the climb process, especially after the large-step climb process, the stochastic perturbation mechanism of the HSA is employed to overcome the premature convergence problem. Watch-jump and the somersault processes are the same as that of the original MA. A Cooperation process is used to improve the interaction among monkeys. The termination criteria occur when the optimal result is obtained or a fixed number of iterations N has reached. When the monkey finds a new and better position, an old position will be replaced by the new one. MMA has been applied for an optimization problem of designing the sensor arrays for the high-rise building known as Dalian world trade building. General sensor selection problems addressing observability are NP-complete and computationally intractable. These problems require fast approximate search [22] solutions. Placing the sensors in the right positions is the aim of the structural health monitoring (SHM) [23] system with modal assurance criterion (MAC) [24] as the objective function.

• D.    Dynamic adaptation of Monkey algorithm

In dynamic adaptation of the monkey algorithm (DAMA) [25], Zheng proposed a chaotic search method to generate random numbers in the initialization process, climb process and watch-jump process. Chaos is defined as the randomness in mathematical point of view which is generated by the simple deterministic systems and three dynamic properties namely, sensitive dependence on initial conditions, ergodicity and semi-stochastic property. Chaotic signals are advantageous than the random signals. Because of these properties of chaos, chaos optimization algorithms (COAs) [26] were presented. The idea of random process is replaced by the chaotic search, for the values of random variables. To generate the chaotic sequences, famous logistic functions [27] were used. Two parameters, namely evolutionary speed factor and aggregation degree are introduced to the evolving state of the monkeys. Evolutionary speed factor in the climb process is the step length, which is adapted for each monkey depending upon its evolutionary state. This is actually designed to get a balance between the convergence precision and convergence speed. The monkey’s evolution state is described by the aggregation degree. Smaller eyesight can make monkeys to get trapped in local mountaintops. As DAMA includes a chaotic search method, it needs enough time to guarantee the ergodicity of the chaotic variable. When the watch times are longer, the search time becomes longer, but the solution obtained will be better. Hence, an adaptive watch time according to the aggregation degree of all monkeys is proposed to obtain a relative balance between the convergence accuracy and speed. If the monkeys cannot get a higher mountain within the range of their eyesight, they will somersault to the boundary of their eyesight and transfer to the new domains to get a global optimal solution.

DAMA was tested by nine unimodal and multimodal benchmark test functions in which the number of local minima increases exponentially with dimensions of the optimization problem.

• E.    Adaptive Monkey algorithm

The adaptive monkey algorithm (AMA) [28] has new operator to provide an automatic adjustment to the climb and watch-jump processes of the original MA. It is difficult to judge the ending time of the climb process and the starting time of the watch-jump process resulting in the less efficient searching process. Monkeys should be able to switch from the climb process to the watch-jump process as soon as it finds another mountain-top. To fulfill this switching between processes, an automatic adaptive control operator is proposed in AMA. A dualstructure coding method is followed to represent the design variables as the sensor placement problem is the single-objective problem with the discrete variable values. In AMA, two new somersault processes, the reflection, and the mutation somersault processes are introduced to improve the global search ability apart from the original somersault process. The reflection somersault process uses the simplex method. The mutation somersault process is the inspiration from the mutation operator of the genetic algorithm to introduce diversity in a population. Each monkey will perform the original, reflection and mutation somersault to generate new positions in the searching domain. The objective function is derived from the modal assurance criteria (MAC) [24]. It is derived by minimizing the maximum off-diagonal component of the MAC matrix. AMA is used for finding the optimal sensor network for the two high-rise buildings in Dalian, China.

• F.    Immune Monkey algorithm

A new hybrid algorithm, Immune monkey algorithm (IMA) [29] is proposed by hybridizing the monkey algorithm and the Immune algorithm [30]. The IMA is proposed in the field of large civil engineering structures to solve the sensor placement problems. Dual-coding method is used to represent the variables in IMA. Chaosbased approach [27] is applied in the monkey population initialization since it has a better universality to the search space where chaos is a natural universal phenomenon. Some updated strategies such as an advanced climb process, immune selection, clonal proliferation and immune renewal are proposed for the population diversity and the degeneracy inhibition. It can incorporate adjustable parameters.

The objective function is called as modal assurance criterion (MAC) [24] which is used to measure the quality and the performance of a specific sensor network design. The original climb process in the MA makes monkey to skip the local optimal solution [18]. To overcome this, the entire climb process is divided into initial climb process and advanced climb process. In the initial climb process, the step length is crucial in the precision of the approximation of the local solution. In the advanced climb process, based on certain probability, the second search is carried out on the initial positions obtained from the initial climb process. To avoid the premature convergence to the local optimal solution during the climb process, Immune algorithm (IA) is adopted in IMA. It is based on vertebrate immune systems that form antibodies to eliminate foreign substances [30]. For each monkey, its position is the candidate solution and in IA it is the antibody. The mountain top is considered as the antigen. As the population diversity decreases during the climb process, the antibodies with high concentration need to be excluded for subsequent processes. The proximity degree between antibodies is calculated by Euclidean distance. The antibody with greater concentration between any pair of antibodies has low selection probability. These antibodies are eliminated through selection strategy to avoid degeneracy. Then, the antibody with the best value is selected to generate new solutions. These new ones can replace the eliminated antibodies to maintain the population diversity. After the Watch-jump process, when the monkey finds a new higher mountaintop and jump onto it from its current position, the advanced climb process is repeated till the mountain top is reached. If the feasible space is bigger, the bigger eyesight value which is determined by the step length value is taken.

Inferior monkeys who cannot find better positions are to be eliminated to maintain the superior monkeys. But this elimination process is not reasonable as the population of the monkeys is limited. Therefore, an immune renewal technique is proposed in IMA and this renewal is applied over the inferior and eliminated monkeys to expose their potential in an iterative manner. After iterations of the above-mentioned processes, each monkey will find a locally maximum position around its starting point. To find a comparatively higher mountaintop, each monkey has to somersault to reach a completely new domain. These modifications of IMA increase the population diversity and restrict the premature convergence problem to provide better solutions to the OSP problem [31] with higher dimensions.

A numerical case study was carried out to determine the sensor configuration using the sensor arrays with node index number as the optimization variable. The sensor configuration is performed for the second highest tower in the world, Canton Tower.

• G.    Niching Monkey algorithm

In health monitoring system setup for large-scale structures, optimal sensor placement (OSP) [31] method plays a main role. To enrich the population diversity and to improve the exploitation capabilities in the original monkey algorithm, a novel niching monkey algorithm (NMA) [32] is proposed. This is the combination of the original MA with the niching techniques. In the sensor placement, the minimization variables are the sensor locations. Dual-structure coding method is followed to represent the variables in NMA. NMA maintains a distributed multi-population approach to increase the diversity through the isolation of subpopulations. Niching mechanism is introduced to improve the information exploitation among neighbors of monkeys. The niching method is based upon the natural Ecosystem [33]. As in an ecosystem with different niches having diverse species, niches are applied in NMA. Within a niche, each individual is forced to share the resources available to them. But among different niches, there will be no conflicts. The novel NMA proposes that each search space be taken as a niche and also proposes to preserve the highly-fit monkeys along with the weaker monkeys as long as they are not the similar ones. As chaotic map has the ergodicity, certainty and randomicity characteristics, it is used to initialize the population in NMA. After the population initialization in NMA, the entire population is classified to form the niches as per the similarity between monkeys. Hamming distance is used to estimate the similarity of binary-coded variables and the real coded variables use the Euclidian distance or any other defined measure. The monkey count in a niche is determined by the resources and the efficiency of each individual in grabbing the resources. The quality of sensor network design is evaluated by an objective or the fitness function MAC [24] which is problem specific. In NMA, the climb process is modified with the help of niching techniques. There are three parts in the climb process of NMA. They are Initial climb process, Fitness sharing mechanism, and Interaction between niches. In the initial climb process, the precision of approximated local solution is determined by the step length parameter. The solutions are more precise when the step length is small. The initial climb process has limits for climbing up and down. In the Fitness sharing mechanism, as it is the best known niche technique to maintain diversity in searching domain, it modifies the search space by reducing the fitness of the monkey in densely populated areas. In interactions between niches, the communication between the niches is maintained with a new scheme, namely “replacement” which interchanges the information about the different areas of the search space between the best and worst niches. The best monkey provides the valuable information to the worst monkey. Hence, the exploitation capability improves. After the climb process, each monkey goes to the mountain top in a niche. Then it will look to find out other higher mountains around. If the feasible space of the problem is bigger, the eyesight should be bigger in the watch-jump process. If the maximum number of generations specified is met without any improvement in the value of the objective function, then the iterations are terminated in NMA and the best solution is returned in a niche.

The computational efficiency of the NMA are demonstrated by two cases of optimal sensor placement on a high-rise structure, Dalian world trade building.

• H.    Monkey algorithm with ABC search operator

A monkey algorithm with the search operator of artificial bee colony algorithm (ABC-MA) [34] is proposed to carry out clustering analysis. Cluster analysis is the process of grouping a set of objects such that the objects in the same cluster or group are more similar to each other than to those in other clusters. The result of k- means clustering depends on the initial solution and is expected to fall into the local optima easily. In ABC-MA, Euclidian metric is used as a distance metric. The objective function used is the minimization of the squared error function. In ABC-MA, the number of clusters and dimensions of the object plays an important role in the computing time of the algorithm. When the climb step is smaller, the climb number will be more to give high precision solution and the computational time is high to calculate the objective value. To reduce the computational time, a new search operator used in artificial bee colony [35] is used before commencement of the climb process. ABC search operator is introduced to strengthen the seek ability to find the local optimal solution. The climb number is also reduced, which in turn reduces the computational time.

The climb process uses a recursive optimization algorithm, called pseudo-gradient based simultaneous perturbation stochastic approximation (SPSA) [36]. The step length of the climb process plays a crucial role in the precision of the local optima. The climb process has a maximum allowable number of climb iterations. Once the climb process is over, the watch-jump process starts and then repeats the climb process till the other mountaintop is reached. In watch-jump process, the eyesight of the monkey is taken as the parameter which depends on the size of the feasible space of the problem. Once the repetition of climb and watch-jump processes is completed and a local optimal high mountaintop is reached, somersault process is initiated to find a much higher mountaintop. For the clustering problem, the center of the objects in the cluster is chosen as the pivot to replace the center of all monkeys by k-means algorithm. Somersault interval is defined in the somersault process to decide the maximum somersault distance of the monkeys.

The results of ABC-MA clustering algorithm is compared with six other stochastic algorithms such as MA, PSO, CPSO, ABC, CABC and k-means algorithms for 2 artificial data sets and 10 real-life data sets (Iris).

• I.    Triaxial accelerometer Monkey algorithm

Triaxial accelerometers are widely used nowadays in the structural health monitoring (SHM) [23] of large-scale structures. Dual-coding method is used to map the OSP problem [31] as it has discrete variables. In triaxial accelerometer monkey algorithm (TAMA) [37], the calculation of the threshold value is done with the help of probability theory. This will reduce the probability of generating disabled monkeys. The EFI3 measurement theory is modified [38] and included in the objective function. In the troop generation process, the new healthy monkeys should be generated randomly. Insemination, pregnancy test, and eugenics are the three steps in the troop generation process. Probability theory related threshold value is proposed to improve the health rate of monkeys. Insemination process is designed for generating a preliminary sensor configuration, which is similar to the oosperm of a monkey. The pregnancy test is to estimate whether the oosperm will form a healthy or a disabled monkey. In Eugenics process, the eligibility of new generated oosperm is estimated and the oosperm will be regenerated until a healthy monkey appears.

A harmony ladder climb process is proposed with the stochastic perturbation mechanism of the harmony search algorithm (HSA) [12]. This is to reduce the premature convergence of the original MA. Each monkey with their climbing experience will try to search the next direction. Harmony ladder climb process considers three factors such as personal best monkey, global best monkey and harmony memory (HM) monkey. The personal best monkey is the monkey’s own location with best positions and best value for the objective function. Global best monkey is the monkey having the best position achieved by each monkey till a certain point of time. Global best monkey is called as ‘monkey king’, which has the capability to build an interaction network to guide the rest of the monkeys. This ‘monkey king’ will be replaced when a new better monkey arrives in each iteration. HM database generates HM monkey based on a rate influenced by the HM considering rate [12]. The biodiversity of the troop of monkeys is improved by this monkey by avoiding premature convergence. After the harmony ladder climb, each monkey reaches the top of the mountain in their local area and look around. When a better location is found, the monkeys will jump to that higher place and restart the simple climbing process. When there are no more higher places that the monkeys can view, they will take rest to save energy. To solve the problem with the eyesight value, a scanning watch-jump (SWJ) process with the adjustable eyesight of the monkey is proposed in TAMA. In this method, the probability of missing a higher mountain in the surrounding area is reduced. Hence, the repeated calculation in a local optimal area is avoided by improving the capability of global optimization. After the harmony ladder climb and SWJ, to increase the chance of a global optimal solution and to make a great change in locations, the monkeys somersault to the center of the troop. After the somersault process, harmony ladder climb and SWJ process are executed. The termination condition in TAMA is achieved when the maximum number of iterations are achieved. TAMA is applied to the sensor placement in the Xinghai No. 1 bridge in Dalian.

• J.    Improved Monkey algorithm

The 0-1 knapsack problem is a classic combinatorial optimization problem. Many algorithms have low precision and easily fall into local optimal solutions while solving the 0-1 knapsack problem [39]. Improved MA proposes [40] binary version of the monkey algorithm to solve the 0-1 knapsack problem which is the combination of cooperation process and greedy strategy (CGMA). In this algorithm, the greedy algorithm is used to improve the ability of the local search, the somersault process is changed to avoid local optima, and the cooperation process speeds up the convergence rate of the algorithm. Random generation of initial population is used in CGMA. As per pseudo-gradient-based simultaneous perturbation stochastic approximation (SPSA) [36], climb process is a step-by-step one. It improves the objective function by selecting a better position among the two positions existing near the current position. Step length is equal to 1 in the knapsack problem. After the climb process and the watch–jump process, the cooperation process is helpful in making the monkeys find a better solution and can improve the convergence rate. It is accomplished by cooperating with the monkey with best position. These monkeys will move forward towards the direction of the best monkey. In 0-1 knapsack problem, there is a chance of getting an abnormal encoded individual which do not satisfy the constraints using the metaheuristic procedures. A local search strategy-greedy algorithm (GTA) [41] is used to improve the feasible solutions by correcting the infeasible ones. In CGMA, the monkey’s position is randomly chosen as the pivot in order to replace the center of all monkeys and a new somersault process is adopted. A “limit” parameter is used to control monkeys falling into the local optima after the repetitions of somersault process. When there is no improvement in the global optimal solution, the monkeys are abandoned and then reinitialized. The CGMA iteration is terminated when the optimal solution is found or a comparatively large number of iterations is reached. CGMA is advantageous in solving 0-1 knapsack problems, fixed and random problems and small and large-scale problems.

• K.    MAKHA (MA and Krill Herd) algorithm

MAKHA [42] is an efficient and reliable optimization method proposed by hybridizing the Monkey Algorithm (MA) and the Krill Herd Algorithm (KHA) [43]. KHA is a bio-inspired algorithm based on the herding activity of krill individuals. The objective function is based on the krill movements that represent the minimum distances of each krill from food and the high density of the herd. The krill motion consists of three main mechanisms such as movement induced by the presence of other krill, their foraging activity, and random diffusion. Two adaptive genetic operators mutation and crossover are used.

MAKHA is a new hybrid and reliable algorithm that combines MA and KHA. MA has two exploration and two exploitation operators. The watch-jump process acts as both the exploration and exploitation operator. The somersault operator with pivot function is a high-performing diversification operator. The exploitation balance is brought to the MA by running the climb process twice per iteration. KHA also has two exploration operators and two exploitation operators, but the physical random diffusion is less efficient than the somersault operator. Hence, KHA can fall into the local optima easily. Two genetic operators (crossover and mutation) of KHA IV [43] can address the trapping problem. KHA has the high-performing exploitation operator, the foraging movement; it is considered as an exploitation-dominant algorithm. The hybrid algorithm, MAKHA, was designed to have these processes:

• •   The watch-jump process.

• •    The foraging activity process.

• •    The physical random diffusion process.

• •    The genetic mutation and crossover process.

• •    The somersault process.

This hybridization used the efficient steps of MA and KHA algorithms and provided a better balance between the exploration and exploitation steps. MAKHA was tested with 27 benchmark problems.

• L.    Chaotic Monkey algorithm

To avoid the slow convergence speed in monkey algorithm (MA), chaotic monkey algorithm (CMA) [44] is proposed. The chaotic monkey algorithm uses chaos search strategy of chaos optimization algorithm [45] to avoid falling into local optima and repeated search in the same domains. The chaotic variable has ergodicity and randomness characteristics which makes the chaos optimization algorithm move out of local optimum solution and fasten the search. In CMA, the initial monkey population is generated using chaotic variable instead of random variable and binary coding to improve the global search capability. Climb process is helpful to explore the local optima with a better position. To improve the climb process efficiency, a greedy local search strategy is used. The best solutions are selected in each step. In CMA the watch-jump process is performed by swapping two bits (0 and 1) with different values independently and chaotically. When the neighbor position of the monkey exhausts and there is no better position, then the monkey does the somersault process to find a new position. The CMA is terminated when the maximum number of iterations is reached. The best solution is updated at each step of CMA. CMA is applied on the optimal sensor placement in a suspension bridge with the objective of minimizing the number of sensors and to locate them in the right places so that the cost could be minimized.

• VI.    Hybrid Monkey Search and Monkey Algorithm

Hybrid monkey search and monkey algorithm combines the tree climbing and the mountain climbing behaviors of monkeys along with the climb, watch-jump, and somersault processes. The algorithms hybrid MS and MA and their applications are shown in the Fig. 11 below.

• A.    Hybrid MSA

The Monkey search algorithm (MSA) [46] is the simulation of a monkey searching for food on top of the trees by climbing, jumping and somersaulting to other trees or mountains. The solutions of the problem are the representation of the locations of food sources. M is the number of solutions, which are the monkeys or agents within a jungle. The output is the feasible position of the monkey to find good food. The starting point is considered as the root of the tree and with the help of the climb process, the monkey climbs the tree step-by-step to reach the top of the tree.

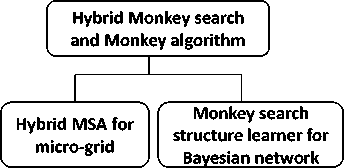
Fig.11. Hybrid MS and MA algorithm and their applications

The step length and the sight length are taken care in the climb process by the monkey. Once the mountaintop or the top of the tree is reached by the monkey, the monkey gets down marking the solution value. When there is a new solution value, it is entered as the current best solution. Once the monkey comes down, it will climb up the tree for n number of times for exploring the branches with the good values. To explore a new search domain, after finding n solutions, the monkey makes a somersault to find a new starting point and starts the climbing process again. Then using a randomized perturbation function and the best solution, the new feasible solutions are created. From the three different perturbations proposed by Mucherino [1], the double point crossover operator is chosen to find the new feasible solution for this Hybrid micro-grid problem. To avoid the local optima, a predetermined number of best solutions are stored in the memory. Replacement of the solutions in the memory by the new best solutions is also encouraged. MSA [46] is applied to the stochastic optimization problems such as configuration of appropriate component for a Hybrid Micro-Grid [47]. In this Renewable Energy Integration Problem, a jungle where the monkey resides is the combination of the generators, wind turbines and PV arrays of the load. The objective of this problem is to supply the energy based upon the demand in an efficient way.

• B.    Monkey search structure Learner

When things are uncertain, based upon the available statistics and the expert’s knowledge, Bayesian belief network (BBN) [48] can provide brief knowledge about a particular domain. Using BBN structure to learn information from the data is basically an NP-hard problem. Hence, it requires an optimization algorithm to arrive at an optimal solution. A hybrid algorithm, Monkey search structure learner (MS2L) [49] has been evaluated over five BBN structure learning approaches. Directed acyclic graph (DAG) is the data structure used in BBN. The aim of MS2L is to present a novel search paradigm for locating the optimal DAG using the monkey search algorithm.

The objective function Bayesian information criteria (BIC) should be maximized for optimal results. To initialize the process of MS, the population size is taken as one. Depending upon the number of monkeys in the population, the same algorithm is run that many times for initialization. The monkey starts creating the branches from the root node with the help of perturb function. The perturbations in MS2L are the single-arc insertion and arc-deletion with equal probabilities. The perturbations is represented as Perturb (Node,dist) where Node belong to the vertices set and dist is the single perturbation to be applied. The monkey climbs over the branch to reach the better solution. The best solution obtained is stored in the memory of the monkey. After the climb process, each monkey is considered to have a sub-optimal solution within a tree. When the trees with better solutions are seen, it will jump to explore the branches. Monkeys are assumed to see only up to its eyesight parameter. One fifth of the number of total variables is chosen as the eyesight. After the climb and watch-jump processes, each monkey reaches its maximal optimal point when compared to the nearby options. Globally optimized values are obtained during the somersault to an unexplored domain. The size of the search space is the deciding factor for the somersault interval. It manages the maximum distance of somersault of a monkey. The objective function is then calculated over newly discovered DAG. When this value is higher than the current best of the monkey, it is used as initialization DAG and the climb process is restarted. From the initial tree, the edges are added if dist value in Perturb function is an arc insertion otherwise it is deleted. This algorithm is terminated for any of these conditions:

• •    Solutions found by all monkeys have not improved since last k iterations

• •    The algorithm has run the maximum permissible times, k.

For evaluation, two parameters are taken into consideration. They are:

• •    The time taken to find the optimal structure.

• •    The performance of the structure

• VII.    Spider Monkey Optimization Algorithm

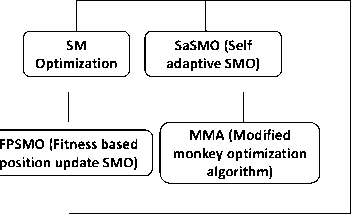
The spider monkey optimization algorithm is based on the spider monkey behavior of splitting themselves into small groups under the local and global leadership of female spider monkeys for searching food. The variations of spider monkey optimization algorithms along with their applications are shown in the Fig. 12. In Fig. 12, the types such as SM Optimization, SaSMO, FPSMO, TS-SMO, and QASMO used benchmark problems and hence it is not mentioned.

• A.    Spider Monkey optimization

Spider Monkey Optimization (SMO) [3] algorithm is inspired by intelligent behavior of fission-fusion social structure based animals. The society of spider monkeys follows the fission-fusion social structure of animals. SMO is a trial and error based collaborative iterative process. SMO process consists of six phases: Local leader phase, Global leader phase, Local leader learning phase, Global leader learning phase, Local leader decision phase, Global leader decision phase. The position update process in Global leader phase is inspired by the G-best guided ABC [50] and modified version of ABC [51].

The SMO algorithm is applied over 26 global optimization benchmark functions which contain both uni-modal as well as multi-modal problems.

• B.    Self-adaptive Spider Monkey optimization

Self-Adaptive Spider Monkey Optimization (SaSMO) [52] algorithm takes very less average function evaluation (AFE) in comparison to basic SMO and Modified position update in the spider monkey algorithm [53]. SaSMO proposed a novel approach for complex optimization problems. It is self-adaptive in nature as it modifies the position of the local leader. The probability based position update is added in global leader phase and the size of search radius is dynamically decreased for a local leader in the iterations. For the entire group members, this algorithm provides the new locality in the Local leader phase. Then the greedy selection mechanism is applied between the existing and the newly computed positions. The probability is calculated using the fitness of the individuals for every group member. In the global leader phase, SaSMO provides new positions for each member of the group. Position of global leader is updated as in basic SMO. The location of the local leader is regulated dynamically with a large step size in the search area in the first iteration. The step size will decrease with the increase in the number of the iterations to provide refined solutions. The idea of SaSMO is that the local leader phase solutions are distant from the best feasible solution in the first iteration and it will converge in subsequent iterations. This SaSMO algorithm is applied to 42 benchmark problems, engineering optimization problems such as Pressure vessel design problem, Compression spring problem and to the real-world problems such as Lennard-Jones problem and Frequency modulated sound waves parameter estimation problems.

• C.    Fitness based position update using SMO

Fitness based Position update in SMO (FPSMO) [54] algorithm introduces a fitness based location updating strategy and updates the position of individuals based on their fitness to improve the rate of convergence and exploitation capability. FPSMO modifies three phases of SMO by incorporating the fitness of individuals. The perturbation in the solution depends on the fitness of the solution. In each solution, the number of updates in the dimensions depends on the probability i.e. the fitness function. The assumption is that the global optima need to be near about the better-fit solutions. When the perturbation of better solutions is high and the step size is larger then there is a possibility of skipping the true solutions. Hence, in FPSMO, the low fit solutions explore the search space and the better solutions exploit the search space. In other words, for the high fit solutions with high probability value, the step size will be small. The modified step size can impose a balance between the exploration and exploitation of search space and also help to avoid the stagnation and early convergence. FPSMO is applied over nineteen different benchmark functions and on a real world problem called Pressure vessel design problem.

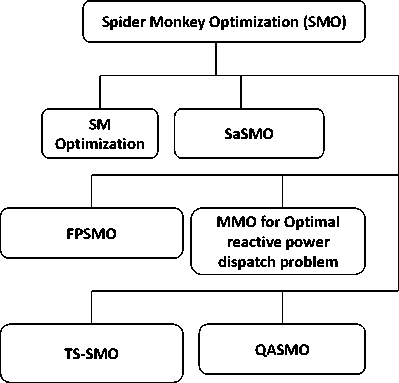
Fig.12. Spider monkey optimization applications

• D.    Modified monkey optimization

Modified Monkey optimization (MMO) [55] algorithm, a stochastic meta-heuristic algorithm can handle nonlinear constraints easily. It improves both local and global leader phases. In this MMO, diversification of the entire search space and intensification of the best solutions are balanced by maintaining diversity in local and global leader phases of SMO. MMO algorithm modifies the local and global leader phases using the modified golden section search (GSS) [56]. The gradient information of the function is not used in Golden section search method to find the optima of unimodal continuous function. MMO algorithm was tested on IEEE 30 bus, 41 branch system having 13 control variables to minimize the active power loss.

• E.    Tournament selection based SMO

Tournament selection based SMO (TS-SMO) [57] replaces the fitness proportionate probability scheme of SMO with the help of the tournament selection based probability scheme. It improves the exploration capability of SMO by avoiding the premature convergence. There are two manipulation phases in each iteration to update the swarm in SMO. In the first phase, based on the probability, the members of the swarm update their positions. This is known as fitness proportionate probability, similar to roulette wheel selection of Genetic Algorithm (GA) [10]. In the fitness proportionate probability scheme in SMO, members with higher fitness have greater chances of updating their position than the low fit ones. In this case, less fit members with some useful and important information may be lost due to their low fitness value. Tournament selection based scheme which took the idea from GA [58] will consider the less fit individuals also to update their positions. This selection is to improve the searchability and convergence speed by providing more exploration. Hence, in TS-SMO the tournament selection based probability scheme is replaced by the fitness proportionate probability scheme of SMO to avoid the information loss from the low fit spider monkeys and allow them to update their position. Tournament of two individuals is done in the TS-SMO. The algorithm is terminated either when the maximum number of iterations is performed or an acceptable error is achieved. The TS-SMO is tested with a huge set of 46 benchmark problems which are unconstrained and with varying complexities.

• F.    Quadratic approximation based SMO

Quadratic approximation based spider monkey optimization (QASMO) [59] is designed by incorporating quadratic approximation (QA) operator in SMO. The idea of applying QA in SMO is based on various stochastic search techniques such as controlled random search, GA, PSO, DE. Introduction of quadratic approximation (QA) operator to SMO algorithm enhances the local search ability. QA provides the minimum of the quadratic curve passing through three feasible solutions in the search space [60]. In QASMO, QA is applied to make use of the information about the current global and local best solutions efficiently. Using QA operator, the neighborhood of these solutions is searched for comparatively better solutions. QA has been implemented in the GLL phase and the LLL phase. In GLL phase, the three solutions including the global leader and two randomly selected members of the swarm are taken. Now the solutions are generated by QA for a predefined number of times till a solution is obtained. A new position is generated using these three solutions. The position of the worst solution is obtained from the swarm. Then, the new position is compared with the position of the worst solution. If the fitness value of a new position is better than the worst solution of the swarm, then the worst position is updated with the new one. In LLL phase, three solutions including the local leader and two randomly selected members of the group are chosen. This is repeated for every group. In QASMO, the GLL and the LLL phases are modified as the updated positions of global and local leader are obtained in these phases respectively. Also,  the number of better solutions obtained is more in these phases. QASMO is applied over the set of 46 scalable and non-scalable benchmark functions and also over the Lennard-Jones problem for three to ten atom clusters.

• VIII.    Comparison of the Various Monkey Behavior Based Techniques

  This section summarizes and compares the different monkey behavior based techniques in terms of their coding method, objective functions, application details, hardware and software used for implementation of each algorithm with the help of a table (Table 1). Starting from the Monkey search algorithm in 2007 till Spider monkey optimization, various coding methods such as binary coding, integer coding, and dual-coding are used to encode the solutions in these techniques. The monkey behavior based algorithms derive some important operators and techniques from other optimization

algorithms such as genetic algorithm, artificial bee colony, Harmony search algorithm, Krill herd algorithm, immune algorithm and Chaos optimization algorithm. The monkey behavior based algorithms are used for variety of applications such as Lennard-Jones and Morse clusters, multi-dimensional assignment problem, optimal sensor placement in high-rise buildings, Bayesian belief networks and so on. Depending upon the applications these techniques have their own parameter values like population size, height of the tree, memory size, step length, eyesight value and so on. Most of the monkey search algorithms are developed using the C++ programming language, while most of the monkey algorithm techniques used the commercial software MATLAB and few Spider monkey optimization algorithms are built using C programming language. The parameters like population size of the monkeys, height of the trees, the size of the memory and the number of times the monkey reach the top of the trees are defined in the case of monkey search algorithm. In the case of Monkey algorithm the parameters defined include the population size, number of generations for the algorithm, step length of the monkeys for the climb process, eyesight of the monkeys for the watch-jump process and the somersault interval for the somersault process and algorithm-specific parameters in the case of chaos optimization algorithm, artificial bee colony, Immune algorithm, Harmony search algorithm, Krill herd algorithm which are hybridized with monkey algorithm. In the Hybrid of MS and MA category, the algorithms have memory parameter along with the Monkey algorithm parameters to carry on the hybrid algorithm heuristics. In the case of spider monkey algorithm, the parameters include swarm size for the number of spider monkeys, global leader limit, local leader limit, the perturbation rate and the total number of runs. Comparison of all the methods suggests that each method has its own advantages and is suitable for finding optimal solutions.

Table 1. Comparison of the monkey behavior based algorithms and their features

S. No	Name of the algorithm	Coding method	Objective functions	Applications	Hardware and Implementation Details
A	Types of Monkey search
1.	Monkey search: A novel meta-heuristic for global optimization	Protein conformation using Dihedral angles representation	Global minimum of the potential energy	Lennard-Jones and Morse clusters, Distance geometry problems and Tube model	C++ on Windows operating system 4GB Duo processor AMD Athlon
2.	Monkey search for solving MAP	Matrix representation	-	Multi-dimensional assignment problems	Intel CPU T2500 at 2 GHz and 1 GB RAM, C++ using CodeBlocks compiler
3	Allocation of capacitor banks in distribution systems through a modified monkey search optimization technique.	Binary structured representation	Minimize the capacitors investment and the cost of system losses.	Allocation of fixed capacitor banks for Electrical power distribution system	3.40-GHz Intel Corei7– 2600 processor with 4 GHz RAM
B	Types of Monkey algorithm
1	Monkey algorithm for global numerical optimization	Binary coding method	Objective functions of f 1 to f 12	12 Benchmark problems or Numerical examples	-
2	Discrete Monkey	Binary coding	Minimize the	Transmission	Developed using Matlab

	Algorithm and Its Application in Transmission Network Expansion Planning	method	investment cost for building transmission expansion scheme for electrical power systems	network expansion planning problem	on PC with Intel Pentium 2.0GHz processor and 2.0 GB of RAM.
3	A modified monkey algorithm for optimal sensor placement in structural health monitoring	Integer coding method	Modal Assurance criteria (MAC)	Optimal sensor placement problem	commercial software MATLAB
4	An improved monkey algorithm with dynamic adaptation	Monkey’s position represented with n dimensions	Objective functions of the corresponding benchmark problems	number of numerical benchmark functions	-
5	Optimal sensor placement for health monitoring of high-rise structure using adaptive monkey algorithm	Dual structured coding method	Modal Assurance Criteria (MAC)	Sensor placement for health monitoring for DITM and DWTB	commercial software MATLAB
6	Health monitoring sensor placement optimization for Canton Tower using immune monkey algorithm	Dual coding method	Modal Assurance Criteria (MAC)	Sensor placement for the whole canton tower	commercial software MATLAB
7	Sensor Placement Optimization in Structural Health Monitoring Using Niching Monkey Algorithm	Dual structured coding method	Modal Assurance Criteria (MAC)	Optimal sensor placement problem for Dalian world trade building	MATLAB
8	A Hybrid Monkey Search Algorithm for Clustering Analysis	hybrid monkey algorithm based on search operator of artificial bee colony algorithm for clustering analysis	Minimizing the squared error function	2 artificial data sets and 10 real life data sets	Desktop computer with a 3.01GHz AMD Athlon(TM) II X4640 processor, 3GB of RAM Matlab 2012a in Windows XP
9	A triaxial accelerometer monkey algorithm for optimal sensor placement in structural health Monitoring.	Dual coding method	Modified EFI3 measurement theory	optimal sensor placement problem	commercial software MATLAB
10	An improved monkey algorithm for a 0-1 knapsack problem.	Binary version of MA	Maximize the value with less weight	Knapsack problem	Desktop computer with a 3.01GHz AMD Athlon(TM) II X4640 processor, 3GB of RAM Matlab 2012a in Windows XP
11	MAKHA—A New Hybrid Swarm Intelligence Global Optimization Algorithm.	Hybrid agent’s position with NV (dimensions of decision variable vector )	Objective functions of the benchmark problems	27 classical benchmark problems	-
12	Chaotic Monkey Algorithm Based Optimal Sensor Placement	Binary coding	Modal Assurance Criteria (MAC)	Optimal sensor placement problem	g++ 4.8.1 compiler
C	Types of Hybrid Monkey search and monkey algorithm
1	Using the Monkey Algorithm for Hybrid Power Systems Optimization (MSA)	combinations of generators, wind turbines, and PV arrays which satisfy the load (1-1-1)	Minimization of the total cost of the system and global warming potential	Hybrid power systems optimization	-
2	A Novel Bayesian Belief Network Structure Learning Algorithm Based on Bio-Inspired Monkey Search Meta-Heuristic.	BBN DAG is represented by connectivity matrix	Maximization of the Bayesian Information Criteria (BIC)	Medical Datasets from UCI machine laboratory are used for evaluation	-
D	Types of Spider Monkey optimization algorithm
1	Spider Monkey Optimization algorithm for numerical optimization.	Spider monkeys represented in Ddimensional vector	Objective functions of the benchmark problems	26 global optimization problems	-

2	Self-Adaptive Spider Monkey Optimization Algorithm for Engineering Optimization Problems.	Spider monkeys represented in Ddimensional vector	Objective functions of the benchmark problems and the real problems	42 benchmark problems and 4 real-world problems	C programming language
3	Fitness based position update in spider monkey optimization algorithm.	Spider monkeys represented in Ddimensional vector	Objective functions of the real and benchmark problems	19 Benchmark functions and a real-world problem	C programming language
4	Modified Monkey Optimization Algorithm for Solving Optimal Reactive Power Dispatch Problem	Spider monkeys represented in Ddimensional vector	Minimize the active power loss and the voltage deviation in PQ buses	Tested on IEEE 30 bus system for optimal reactive power dispatch problem	-
5	Tournament Selection Based Probability Scheme in Spider Monkey Optimization Algorithm.	Spider monkeys represented in Ddimensional vector	Objective functions of the benchmark problems	46 unconstrained benchmark problems	-
6	Improving the local search ability of spider monkey optimization algorithm using Quadratic approximation for unconstrained optimization	Spider monkeys represented in Ddimensional vector	Objective functions of the benchmark problems	46 scalable and unscalable benchmark functions and Lennard-Jones problem	-

In the case of Monkey search algorithms, as the climbing of the monkeys over the trees are decided by the metaheuristics such as SA, GA, ACO, DE or HAS based perturbations, it is applied to the hardest global optimization problems such as Lennard-Jones clusters and Morse clusters and also to the tube model for protein folding. Monkey search algorithm can also be applied to solve the general multidimensional assignment problem instances. As each feasible solution of MAP uses the matrix representation, this representation is helpful in constructing perturbations. In the Modified monkey search version, the MS algorithm is modified to suit the technical characteristics and limitations of the optimal capacitor allocation problem with varying bus bars and distribution networks/branches/feeders in electrical power distribution systems.

In the second category of monkey behavior based algorithms, Monkey algorithm was applied to the benchmark numerical problems with continuous variables including Sphere function, Ackley’s function Rosenbrock function etc. DMA is the modified version of the MA, with the particular load level and generation expansions, Transmission expansion planning problem build new transmission infrastructure with minimal investment cost. MMA is an algorithm applied to increase the structural safety and reliability of the high-rise civil structures with minimal operation and maintenance costs for Dalian world trade building located in northeast of China. DAMA, which is the monkey algorithm’s version with dynamic adaptation was applied to the several test functions of nine numerical problems some of them taken from original MA test problems. AMA is applied to allocate sensors across Dalian world trade building and Dalian International trade mansion efficiently. IMA is the immune version of MA and is applied to allocate sensors to the whole tower and to the main tower of the Canton Tower in China. NMA is the modification of MA with niching techniques for better population diversity was also applied to the structural health monitoring system to implant the sensors over Dalian world trade building efficiently. A hybrid monkey search algorithm with the search operator of ABC was applied to perform the cluster analysis over two artificial datasets and ten real-life data sets such as IRIS, Teaching Assistant evaluation, Wisconsin breast cancer data sets etc. The triaxial accelerometer monkey algorithm with the monkeys having improved health rate is applied to the optimal sensor placement over the world’s first self-anchored bridge called Xinghai No.1 bridge in Dalian, China. CGMA is the binary version of MA with cooperation process and greedy strategy is applied to solve the 0-1 Knapsack problem which is an operations research NP-hard problem. MAKHA is the hybrid of the Monkey algorithm and the Krill herd algorithm developed to incorporate the salient features of both the algorithms is applied to twenty-seven classical benchmark functions to prove its performance. CMA is the Chaotic monkey algorithm with chaotic variables is applied to the sensor placement problem over a suspension bridge.

In the hybrid of Monkey search and monkey algorithm category, Monkey climbing up the trees using climb process and somersault process which is named as Monkey search algorithm is applied to the hybrid microgrid to find the appropriate component configuration. Under the same hybrid category, MS2L, Monkey search structure learner is applied over five Bayesian belief networks structure learning approaches.

In the last category, Spider monkey optimization algorithm based on the social behavior of the spider monkey is tested on 26 global optimization problems. Another version of SMO called Self-adaptive SMO with no manual setting of its parameters was tested on forty-two benchmark problems and four real-world problems to prove its efficiency. FPSMO, the other version of SMO with fitness position updates is tested over twenty-three diverse benchmark functions and a real world problem, Pressure vessel design problem. Modified monkey optimization algorithm, the modified version of SMO with Golden section search was applied to the optimal reactive power dispatch problem. In TS-SMO, the performance of the tournament selection based SMO was tested with 46 scalable and non-scalable optimization problems. In QA-SMO, Quadratic approximation operator incorporated SMO performance is tested with 46 unconstrained optimization problems and applied to the Lennard-Jones problem to find the relative position of atoms in a cluster.

• IX.    Conclusion

Several swarm intelligence based algorithms such as particle swarm optimization, ant colony optimization, Glowworm swarm optimization etc, are used for finding optimal solutions to various complex optimization problems. Monkey behavior based algorithms, one of the swarm intelligence algorithms, are based on the behavior of monkeys in finding food from trees/jungle/mountains and are useful in deriving optimal solutions from huge search space. The Monkey search optimization algorithm has the feature of incorporating other efficient swarm intelligent algorithms in its metaheuristic structure; the researchers can give a hand to improve this algorithm with some special features of the other algorithms. Monkey algorithm and its variations are designed to solve optimization problems with discrete and continuous variables. Also, these algorithms are hybridized with various operators and representations obtained from other well-known swarm intelligence algorithms such as artificial bee colony optimization and immune algorithms.

Hybrid of MS and MA type algorithms combine the features of both the monkey search and monkey algorithm features together to provide researchers more options for development. Spider monkey algorithm is a recent addition in this series, which is based on the spider monkey behavior of searching food in small groups and is claimed to have the exploration and the exploitation capabilities in a balanced manner by providing the results in remarkable time. The evolution of the monkey behavior based algorithms over the time in terms of functionality is discussed in detail along with their representations, operators, and techniques. Each of these algorithms is applied in divergent fields like protein conformation, electrical distribution system, hybrid micro-grid, optimal sensor placement in high-rise buildings and large-scale civil structures, Bayesian belief networks. Further, these algorithms could be made more efficient in finding solutions by incorporating other intelligent behaviors of monkeys and also by hybridizing with other swarm intelligence algorithms. Also, their exploration and exploitation capabilities can be studied and improved by the researchers in future and can be applied to various unexplored real-life optimization problems.