Монотонная сплайн-интерполяция класса C2 на основе однопараметрических групп диффеоморфизмов

В теории сплайн-интерполяции задачи формосохраняющей (или изогеометрической [1, с. 8]) интерполяции, в которых от интерполянта требуется, чтобы он обладал некоторыми геометрическими свойствами (положительность, монотонность, выпуклость и другое), присущими интерполируемой функции, считаются в настоящее время изученными достаточно хорошо [2] . Рассмотрим, в частности, задачу монотонной интерполяции .

Предполагается, что на отрезке [а, 6] числовой прямой R заданы функция /: [а, 6] ^ R и сетка Л из конечного числа узлов Х _г : а = Х 0 <  Х 1 < ... < Х ^ = b (так что указанный отрезок разбит на п отрезков разбиения [Х ^ , Х ^ +1 ], г = 0,..., п — 1), причем значения У = /(Х ^ ) функции / в узлах сетки известны. Требуется найти интерполянт — такую сплайн-функцию F , которая принимает в узлах сетки те же значения [3, с. 347–350, 390–391, 485].

Например, для кубических сплайнов их сужения на каждый отрезок разбиения ( звенья ) являются кубическими многочленами вида

F _t (x) = а _г + 6 _г (х — Х _г ) + с _г (х — Х ; ) ² + й _г (х — Х _г ) 3 ;                     (1)

коэффициенты звеньев не произвольны, а подчинены условиям непрерывности низших производных сплайна F во внутренних узлах сетки. Если в роли интерполянта F выступает кубический сплайн дефекта 1 (такие сплайны являются дифференцируемыми функциями класса С2, а образуемое ими векторное пространство далее, как и в [4], мы обозначаем Pg\), то непрерывными должны быть его первая и вторая производные; задание (наряду с условиями F(Xi) = У) двух граничных условий, налагаемых на сплайн в точках а и Ь, позволяет однозначно найти искомый интерполянт [3, с. 390—393]. Интерполяция здесь является нелокальной: значения коэффициентов сплайна зависят от всех значений У [5, с. 32].

Для кубических сплайнов дефекта 2 (они являются дифференцируемыми функциями класса С ¹ и образуют [4] векторное пространство P 3^X₂ ) естественной является задача эрмитовой интерполяции — когда в узлах заданы также значения У ’ = / ‘ (Х _г ), а от интерполянта, кроме выполнения условий F (Х _г ) = Уг , требуют, чтобы значения его первой производной в узлах (называемые наклонами сплайна [3, с. 391]) были такими же: F ‘ (Х _г ) = У/. Здесь уже интерполяция носит локальный характер и может быть проведена для каждого отрезка разбиения независимо [5, с. 25–26].

Теперь предположим, что интерполируемая функция / либо строго возрастает на отрезке [а, Ь], либо строго убывает:

V i У г +1 >  У_г либо V i У_г+1 < У_г , (2) и надо обеспечить строгую монотонность интерполянта F ; это и есть задача монотонной интерполяции (точнее говоря, ее частный случай: строго монотонная интерполяция, когда все знаки неравенства являются строгими; как и в [4] , мы ограничиваемся здесь именно этим случаем).

Кубические сплайны обеспечивают сохранение формы далеко не всегда [1, с. 141–145, 151]. Заметим, что необходимые и достаточные условия монотонности для сплайнов из Р ^₂ найдены Ф. Фричем и Р. Карлсоном в 1980 году (см. [6] ), а в работах В. Л. Мирошниченко 1984 и 1990 года (см. [7, 8] ) получены достаточные условия монотонности при интерполяции сплайнами из P3\; в 2001 году Ю. С. Волков получил, исходя из иного представления интерполяционного сплайна, другой вариант таких достаточных условий [9, 10] .

В этой ситуации были предложены различные подходы к решению возникшей проблемы. Фрич и Карлсон отказались от выполнения условий F ‘ (Х _г ) = У ’ и предложили алгоритм локальной монотонной интерполяции класса С ¹ кубическими сплайнами дефекта 2, в котором наклоны сплайна во внутренних узлах сетки выступают как свободные параметры, выбираемые так, чтобы обеспечить монотонность интерполянта. Развитием данного подхода стала интерполяция весовыми кубическими сплайнами [11] .

В основе другого направления исследований лежало обобщение конструкции кубических спланов, и на этом пути было предложено несколько типов обобщенных кубических сплайнов: рациональные, с дополнительными узлами, экспоненциальные, гиперболические и другие [12] . Наибольшее внимание привлекли рациональные сплайны, звенья которых — дроби с кубическим многочленом в числителе и многочленом 1-й или 2-й степени в знаменателе; здесь следует упомянуть работы [13 –15] , где рассматривались локальные схемы интерполяции и были построены сохраняющие монотонность эрмитовы ин-терполянты класса С 1 , и работы [ 16, 17] , где предложены нелокальные монотонные интерполянты класса С ² (для их получения нужно — как и в случае кубических сплайнов дефекта 1 — решать систему линейных уравнений с трехдиагональной матрицей). Однако при интерполяции рациональными сплайнами возникает достаточно сложная проблема управления дополнительными свободными параметрами, характерными для такой интерполяции.

В статье [4] автором была предложена иная процедура эрмитовой сплайн-интерполяции класса С 1 , гарантирующая для строго монотонных данных строгую монотонность получаемого интерполянта. Здесь i-е звено искомого интерполянта F имеет вид

F (т) = У г + (У г +1 - У г ) F(s) , (3) где s = (т — Х _г )/(Х _{г +1} — Х _г ), а F — диффеоморфизм (заданной степени гладкости г) единичного отрезка I = [0, 1], сохраняющий ориентацию и являющийся суперпозицией диффеоморфизмов (функциональных сомножителей) из некоторых выбранных заранее однопараметрических групп.

′′

Выбор сомножителей должен обеспечить выполнение условий F _г (0) = р _г , F _г (1) = д _г (в задаче эрмитовой интерполяции р _г = У//Д _г и д _г = У +1 / Д .^ , где Д _г = (У +i —У _г )/ (Х _г +1 —Х _г )). В [4] предпочтение было отдано суперпозициям типа «сэндвича»:

̂︀

~

F i = F g . о F _{7 i} о F g . ,

̂︀

где F g . — функциональный квадратный корень из функции F g . (то есть функция F g . = F ^^ ), а F g . и F _7i — элементы однопараметрических групп типа G ^a и G ^s соответственно, причем р _г = ^ Р г /<1 г и

^ i = aJ p _i q i — значения соответствующих параметров (мультипликативных). Для элементов групп типа G ^a и G ^s по определению имеют место соотношения

П (0) = (З_г , F^ (1) = 1/Д,                                (5)

F ^ (0) = F ^ (1) = ^ i ,                                   (6)

откуда и следует выполнение условий F _i (0) = p _i , F _i (1) = q _i .

Автор хотел бы отметить, что его интерес к интерполяции сплайнами наметился в 1990-е годы и стимулировался прежде всего их применениями к задачам построения программного движения манипуляционных роботов (см. [18 –20] ). Идея построения локального монотонного интерполянта как «сэндвича» из диффеоморфизмов, принадлежащих определенным однопараметрическим группам, оформилась к 2000 году; тогда же было решено использовать группы G ₁ ^a (в [4] она обозначалась G ^a ), G ₁ ^s и G ₂ ^s (чуть позднее функции из этих групп нашли применение при решении некоторых задач управления движением механических систем [21 –23] ). Но законченный вид описанная в [4] процедура эрмитовой сплайн-интерполяции класса С ¹ обрела в апреле—мае 2017 года.

Настоящая же работа посвящена интерполяции класса С ² сплайнами вида ( 3) ,( 4 ) и отражает результаты исследований, проведtнных в июле–августе 2017 года.

• 2.    Выбор групп диффеоморфизмов

Итак, рассмотрим для строго монотонной функции / интерполяционный сплайн F вида ( 3 ),( 4 ), но уже не требуем, чтобы его наклоны во внутренних узлах сетки совпадали со значениями ¥‘. Будем использовать для наклонов данного сплайна обозначение m _i (именно так обычно обозначают наклоны кубических сплайнов [5, с. 31]).

Тогда для производных локального интерполянта F _i на концах отрезка I имеем: p _i = m _i /A _i и q _i = m _{i +}i /A _i . Элементы F _k однопараметрических групп диффеоморфизмов этого отрезка, то есть функции вида у = F _k (ж), где к — параметр группы (мы сейчас временно обозначаем их аргумент ж, а не s), являются [4, 24] решениями соответствующего уравнения Шрёдера

Ф(у) = к Ф(ж),                                         (7)

где Ф — функция Шрёдера (своя для каждой группы). На функцию Ф далее налагаем условия нормировки: Ф(0) = 0, Ф' (0) = 1 (нормированную таким образом функцию Шрёдера называют еще функцией Кёнигса [25, 26] ); в этом случае параметр к совпадает со значением производной функции F _k при ж = 0.

Как уже отмечалось, среди однопараметрических групп диффеоморфизмов отрезка I в [4] выделялись группы типа G ^a и G ^s , элементы которых удовлетворяли соотношениям ( 5 ) и ( 6) соответственно. Однако приведенные в [4] конкретные примеры таких групп в действительности, как мы сейчас покажем, обладают более сильными свойствами симметрии.

Именно, наряду с группой Diff + ( I ) всех диффеоморфизмов единичного отрезка I , сохраняющих ориентацию, рассмотрим более широкую группу Diff ^т ( I ) диффеоморфизмов этого отрезка, включающую также и диффеоморфизмы, которые ориентацию не сохраняют. Простейшим примером последних служит функция l , определяемая равенством l (ж) = 1 — ж. Очевидно, l о l = id, где id — тождественное отображение отрезка I на себя, то есть функция у = ж; отсюда следует, что l ^-1 = l .

Заменив в уравнении Шрёдера ( 7 ) функцию Ф функцией Ф о L и решив полученное уравнение, приходим к новой функции F ^ из Diff + ( I ), связанной с исходной функцией F _k соотношением F k = l о F _k о l ^-1 (по терминологии, принятой в общей алгебре, отображение I _L , определяемое для элементов д группы Diff ^r ( I ) формулой I _t (y) = l о д о l ^-1 , называется внутренним автоморфизмом данной группы, порожденным ее элементом l , а элемент I _t (g) — элементом, сопряженным к элементу д [27, с. 444, 454]; для группы Diff + ( I ), впрочем, I _L является внешним автоморфизмом). Будучи автоморфизмом, отображение I _L удовлетворяет тождеству I _L (g 1 од ₂ ) = I _t (g 1 ) о I _t (g ₂ ).

Таким образом, F _k (ж) = 1 — F _k (1 — ж), откуда получаем следующие соотношения:

^F k ' ^{( ж )} = ^F k ^{(1 — ж )} ,      ^F k "^{( ж )} = ^{— F}k ^{(1 — ж )} .                          ⁽⁸⁾

Теперь выпишем явные выражения для функций из групп G ₁ ^a , G ₁ ^s и G ₂ ^s , указывая каждый раз вид соответствующей нормированной функции Шрёдера:

S is :

_{G 2}s _:

G a : ^F <*> = н/Ь

<ж <ж

, х         ж

^{Ф( ж )} = 1 - ж;

ж- 1 /

^{2    2} V (?ж(1 - ж)) ² + (ж - 1 / 2 ) 2 + 7ж(1 - ж)

,

ж (1 - ж)

^Ф = 12

;

F'(ж) = 2 + 2 ^

ж - '2

, - ж) + (ж - 1 / 2 ) 2

Ф(ж)

ж (1 - ж) (1 - 2ж) ² ’

здесь через /3 и 7 обозначены параметры групп.

Выполняя в каждом из этих трех случаях рассмотренный выше переход от функции Ф к функции Ф о L, убеждаемся, что для функций из данных групп справедливы тождества

Fp (ж) = Fp-(ж) = F 1/э (ж) и F° (ж) = F7 (ж);

выполнение данных тождеств означает, что для функций из группы G ₁ ^a справедливо следующее свойство симметрии:

Fp(ж) = 1 - Fi/p (1 -ж), а для функций из групп G1s и G2s имеет место такое свойство:

F7(ж) = 1 - F7(1-ж).

В дальнейшем условимся называть группой типа G ^a любую однопараметрическую группу сохраняющих ориентацию диффеоморфизмов отрезка I , элементы которой обладают свойством ( 13 ), а группой типа G ^s — соответственно любую однопараметрическую группу, для элементов которой выполняется свойство ( 14 ). Соотношения же ( 5 ) и ( 6 ) оказываются при этом простыми следствиями свойств ( 13 ) и ( 14 ).

Обозначим через M⁷⁷ и M ^2 ^ множества интерполянтов вида ( 3 ),( 4) , которые являются дифференцируемыми функциями класса С^т и построены по сетке Д для всевозможных наборов данных У 0 ,..., Уф, удовлетворяющих условиям ( 2 ), при выборе групп S a и S is (соответственно, S a и S 2S ) в качестве конкретных реализаций групп типа S ^a и S ^s . В случаях, когда конкретное значение т несущественно или ясно из контекста, соответствующий индекс будем опускать.

На практике важна также быстрота вычисления значений сплайна F . Если в случае кубических и рациональных сплайнов для этого используются лишь четыре основные арифметические операции, то в случае интерполянтов из множеств М ^ и М -⁷ добавляется еще операция извлечения квадратного корня (не требуется вычислять значения трансцендентных функций, как, например, в случае тригонометрических сплайнов [28, 29] ).

Расчетные формулы остаются достаточно простыми. Приведем фрагмент программы на языке Си, в котором реализуется вычисление значений сплайна из множества М 1⁷ для текущего значения аргумента ж. Имеем:

N = beta * s, u=N/(1.0+N-s);

P = u - 0.5, Q = gamma *u*(1.0-u);

v=0.5+0.5*P/( sqrt(Q*Q+P*P) + Q );

N = beta * v, w=N/(1.0+N-v);

y = Y[i] + ( Y[i+1] - Y[i] ) * w;

Здесь предполагается, что заранее рассчитанные значения параметров 3 = V A и 7 ^ уже считаны из соответствующих массивов и вычислено текущее значение s.

Для сплайна из множества М ⁷2 оператор в третьей строке приведенного фрагмента следует заменить таким:

v=0.5+0.5*P/ sqrt(Q+P*P);

• 3.    Соотношения непрерывности

Получим для интерполяционного сплайна F вида ( 3 ),( 4) соотношения, при выполнении которых данный сплайн будет на отрезке [а, Ь] дифференцируемой функцией класса С 2 . Если для кубических сплайнов такие соотношения можно получить, приравнивая в каждом внутреннем узле Х _г выражения для вторых производных звеньев F _{г -1} и F [3, с. 392], то нам будет удобнее оперировать производными от логарифмов первых производных звеньев искомого монотонного интерполянта. Иными словами, рассмотрим функции, определяемые соотношениями ′′               ′

• 8г(х) = Fк(х) /F' (х)    и     S^s) = F _г (s) /F _г (s).                   (15)

Поскольку

Fг (х) = Дг Fг (s) ,     Fг (х) = Дг Fг (s) / Кг, где Кг = Хг+1 — Хг, то получаем:

8 г (х) = 8 г (s) /К г .

Следовательно, условие 8 _{г- 1} (Х _г ) = 8 _г (Х _г ) переходит в такое соотношение непрерывности:

8 г - 1 (1) К г = 8 г (0) К г - 1 .                                       (16)

Поделив обе части равенства ( 16 ) на К _г +К _{г- 1} , получаем иную форму данного соотношения:

А г 8 г - 1 (1) = М г 8 г (0) ,                                         (17)

где

_А = К г              =     К г - 1

^К г + ^К г - 1 ,             ^К г + ^К г - 1

С учетом формулы ( 4 ) для локального интерполянта имеем:

ВД = FPi (х),    где х = F- (у) , х = FPi (s), откуда последовательно находим:

^F г ^{( s )} = ^{F ( х )} • ^F - ^{( х )} • ^{F ( s )} ,

′′                 ′′ 2 ′ ² ′                            ′ ² ′                            ′′

^F г ^{( s )}   = ^{F ( х )} • ^F - (^х) • ^{F ( s ) +} IF ^{( х )} • ^F _{7 1} ^{( х )} • ^F . ^{( s ) + F}/3 . ^{( х )} • ^F - ^{( х )} • F ^ ^{( s )} ;

в результате имеем:

^S"   = ⁸ . ^{( х )} • ^F - _г ^{( х )} • ^F p _% ^{( s ) + 8} - _г ^{( х )} • ^F p _% ^{( s ) + 8} р _г ^{( s )} .                     ⁽¹⁹⁾

Для подстановки в соотношение непрерывности ( 17 ) нужны значения правой части равенства ( 19 ) в точках 0 и 1. Чтобы найти эти значения, не обязательно вычислять в явном виде значения всех фигурирующих в данном равенстве функций при произвольном значении аргумента, поскольку быстрее приводят к нужному результату следующие рассуждения.

Разложения по Маклорену нормированной функции Шрёдера и обратной к ней функции имеют вид:

Ф(х) = х + к X + ... и Ф 1 (z) = z — к X + ... ,                 (20)

где к = Ф"(0)/2. Поэтому для решения F ^ уравнения Шрёдера ( 7 ) мы имеем:

F k (х) = Ф ^— 1 (А' Ф(х)) = Ф ^{- 1} ( кх + к к х ² + . ..) = = (кх + к кх + .. .) — к ( кх + к кх + .. .) ² + ... =               (21)

= кх + к (1 — к) кх ² + ... ;

почленное дифференцирование разложения ( 21 ) дает:

F к (х) = к + 2 к к (1 — к) х + ... ,      F к (х) = 2 к к (1 — к) + ...

и, следовательно,

F к (0) = к,     F к (0) = 2 к к (1 — к),      8 к (0) = 2 к (1 — к).               (22)

Для получения соответствующих формул при значении аргумента, равном 1, перейдем к сопряженной функции F _k и воспользуемся соотношениями ( 8) ,( 12) . В случае группы типа G ^a получим:

F g (1) = 1/3,     F g (1) = 2 к a (1 -/ 3 )/3 ² ,      S _p (1) = 2 к a (1 - /3)//3,          (23)

а в случае группы типа G ^s будем иметь:

F I (1) = 7,     F ^ (1) = - 2 к s 7 (1 - 7),    S ₇ (1) = - 2 к s (1 - 7)           (24)

(значения параметра κ для каждого из этих случаев мы различаем с помощью нижнего индекса).

Далее в качестве группы типа G ^a мы будем рассматривать группу G 1^a (для которой к a = 1), а конкретный выбор группы типа G ^s пока отложим.

В силу ( 19 ) для значений S i (0) и S t (1), учитывая формулы ( 22) — ( 24 ), получаем:

ft (0) = 2(1 -ft ) - 7 •& + 2 к s (1 - 7) •& + 2(1-Д) =

= 27 ft - 27 ft + 2 к s (1 - 7) ft + 2 - 2 ft =

= 2 - 27 ft + 2(1 - 7 » )(к s - 1) ft ,

™ _ 2(1 - 3 t )     1   _{9 n}          2(1-Д) _

St(1) =            • 7t •    - 2 кs(1 -7t) •    +             = ft          ft                   ft ft

= 27/ft - 27/ ft - 2 к s (1 - 7 t )/ A + 2/3 t - 2 =

= - 2 + 27/ft - 2(1 - 7 » )(к s - 1)/ Д

(здесь ft = V 3D-

Соотношение непрерывности ( 17 ) принимает вид:

^A t (^{- 2 + 2} 7 t - i /3 t - i ^{- 2(1} - 7^ 1 ) ^{( к} s ^- ft/ft - i ) = щ ( 2 ^- 2 7 t ft ^{+ 2(1 -} 7 t ) ^{( к} s ^- 1) ft) .    ⁽² 5)

4. Уравнения для обратных наклонов

Если в случае кубических сплайнов класса С ² соотношения непрерывности служат основой при получении системы уравнений для наклонов m _t интерполяционного сплайна, то нам будет удобнее работать с обратными наклонами — величинами N _t = 1/ | m _t | (знак модуля здесь актуален для монотонно убывающих данных). После нахождения величин N _t обратный переход к наклонам m _t , разумеется, не составит труда.

Выразим отдельные величины и выражения, входящие в соотношения ( 25 ), через обратные наклоны N _t . Имеем:

Pt = mt/|At| ,  qt = mi+i/|Ai|, ft = VPt/qt = Vmt/mt+i = Nt+/12 Nt-1/2 , ft = Vft = N^ Nt 1/4 ,  7t = VPt qt = Vmt mi+i/|Ai| = Nt+1/2 N 1/2/ |At |,

7 t - i /3 t - i = (N t ^{- 1 / 2} N t Z 1 / ² / | A t - i |) /(N t ^{1 / 2} N t Z 1 / ²) = N t ^{- 1} / | A_i | ,

(︁

N t +1 / 2 N t ^{1 / 2} / | A t |)^ N t + / i² N t ^{1 / 2}) =N t ^{- 1} / | A t | .

Теперь подставим все эти выражения в равенство ( 25) (не трогая пока множители 1 - 7 _{t- 1} и 1 - 7 _t ), раскроем внешние скобки, соберем все слагаемые в одной части равенства и учтем, что A _t + ^ _t = 1:

2 - 2 A t N t ^{- 1} / | A t - i | - 2 _M t N t ^{- 1} / | A t | + 2 A t (1 - 7 t - 1 )(к s - 1) N t - ¹ / ⁴ N — +

+ 2 _M t (1 - 7 t )(к s - 1)N t + ^/4 N t^{- 1 /} 4 = 0 .

Умножим обе части полученного равенства на N _t /2:

^N t ^{- A} t / ^{| A} t - i | ^- P t / ^{| A} t | ^{+ A} t ^{(1 -} 7 t - i ) ^{( к} s ^- 1) ^N _t 3 / ^N _t —₁ ⁺

+ p t (1 - 7 t )(к s - 1)N t +^/4N t ^{3 / 4} = 0 ,  / = 1,...,n - 1.

Обсудим смысл отдельных слагаемых в уравнениях ( 26 ).

В литературе по эрмитовой сплайн-интерполяции описаны три основных метода приближенного вычисления наклонов m _i интерполяционного сплайна для случая, когда значения Y i первой производной интерполируемой функции во внутренних узлах сетки недоступны: метод среднего арифметического (Arithmetic Mean Method, AMM), метод среднего геометрического (Geometric Mean Method,

GMM) и метод среднего гармонического (Harmonic Mean Method, HMM) [30] . Они сводятся к за-

мене наклонов mi величинами т0, где [15,29,30]: т0 = Ai Ai-x + —i Ai , (AMM) (27) т0 = A- x Ar, (GMM) (28) т0 = = Ai-x Ai / A* , (HMM) (29) а A* = (Y+x -Yi-x )/(Xi+x-Xi-x).

Методу HMM соответствует такое значение обратного наклона:

| A * |      = | (Y +x - Y i ) + (Y -Y - 1 ) |

^{| A} i ^{|| A} i - 1 |           ^{( h} i ⁺ h i - 1 ) ^{| A} i ^{|| A} i - 1 |

^h i ^{| A} i ^{| + h} i - 1 ^{| A} i — x |    A i          hi

(h i + н _г - 1 ) | A i || A i- i | = i AZT i ⁺ j A “| ^;

таким образом, 2-е и 3-е слагаемые в ( 26 ) можно интерпретировать как взятое со знаком «минус» значение обратного наклона, вычисленное методом HMM.

В [4] для сплайна из множества Mfp (или M^2)указан способ приближенного вычисления наклона в узле Xi, при котором этот наклон вычисляют как значение в данном узле производной от вспомогатель- ного интерполянта вида

Е^ж) = Y i - x + (Y i +x - Y i )Ер ( ^{Г X i}-^x ) , \^Xi +x ^{- X} i - x /

где Е р е G 1^a , а параметр р задают выражением „ у (1 - ж)           _

Р =          , где ж ж (1-У)

X i - X i - 1

Y i - Y i - x

------------, У = ----------- X i +x - X i - x ’ ^У Y i +x -Y i - x

.

Действуя данным способом, находим:

E _№ ) = ^А * ^{Е р (ж)} = ^А * (1 + р^р - ж ) ₂ ;

выполнив несложные преобразования, нетрудно убедиться, что E ( i ) (X _i ) = A _{i- x} A _i / A * . Данное обстоятельство дает, кстати, прозрачную интерпретацию для метода HMM.

Обратимся теперь к 4-му и 5-му слагаемым в уравнениях ( 26 ). Заметим, что при достаточно густой сетке эти нелинейные слагаемые малы. В самом деле, разлагая Е (ж) и Е ' (ж) в точке ж = X _i по Тейлору и полагая ж = X _{i +x} , получаем:

Е (X i +x ) = Е (X i ) + Е ' (X i ) h i + Е '' (X i ) h 2 /2 + Е ''' (X i ) h 3 /6 + О (h ^    и

Е ' (X i +x ) = Е ' (X i ) + Е '' (X i ) h i + Е ''' (X i ) h 2 /2 + О (h⁰), откуда для параметров р и ^ _i находим:

Р = 1 - ^{Е ( X i )} hi + О (h ⁰ ) и _7г = 1 + —(^ h + О (h 3 ). (33) Pⁱ 2Е ' (X _i ) ^{i V i!} ’ 12Е ' (X _i ) ^{i V i! V 7}

Из формул ( 33 ) следует, что при измельчении сетки p _i ^ 1 и 7 _i ^ 1, причем 7 _i стремится к 1 значительно быстрее, чем p _i . При этом 4-е и 5-е слагаемые в ( 26 ) за счет наличия в них множителей 1 - 7 _{i- x} и 1 - 7 _i быстро становятся малыми.

Данное обстоятельство позволяет применить для решения уравнений ( 26 ) метод простых итераций [3, с. 243–244] и сделать вывод о том, что решение этих нелинейных уравнений в случае густой сетки существует и единственно (впрочем, скорость сходимости метода простых итераций невелика, и на практике, как мы увидим позже, значительно лучшие результаты дает применение метода Ньютона). Вопрос же о разрешимости уравнений ( 26 ) при больших значениях шага сетки требует дальнейших исследований.

• 5. Решение уравнений для обратных наклонов

Переходя к решению уравнений для обратных наклонов сплайна, конкретизируем выбор группы типа G ^s . Сначала рассмотрим случай группы G 2S , для которой к _s = 3.

Подставим в уравнения ( 26 ) это значение параметра к _s и выражения множителей 1 — 7 ^ - 1 и 1 — 7 ^ через обратные наклоны N t . Дополним систему соотношениями для обратных наклонов N 0 и N , (мы ограничиваемся случаем граничных условий I типа , когда заданы значения первой производной интерполируемой функции в узлах Х 0 и Х , и требуется, чтобы значения первой производной сплайна F в этих узлах были такими же: F ‘ (Х 0 ) = У д , F ' (Х _л ) = У , [5, с. 31]); тогда система уравнений для обратных наклонов примет вид

N g — 1 / | У | = 0 ,

N — А _г / | А^ 1 | — щ / | А _г | + 2 А _г Л\ 3 4 N^ t — 2 А _г N^⁴ N^⁴ / | А _г- 1 | +

+ 2 щ Л\ 3 4 N + — 2 щ Л . ' 4 a/V | А _г | = 0 ,          i = 1,...,п — 1 ,

N , — 1 / | У , | = 0 .

Данная система нелинейных уравнений допускает компактную запись в виде единого уравнения Ф (Х) = 0, где роль столбца Х играет набор значений N_o,..., N „ . Для ее решения будем использовать метод Ньютона [3, с. 249], расчетные формулы которого представим в форме:

Х ^к +1 = х ^к + _{P k} ,    _{P k} = — Ф(Х ^к )\Ф ‘ (Х ^к ),

где к — номер итерации, р _к — вектор полного шага (разность значений Х на двух последовательных итерациях), Ф ' (Х ^к ) — вычисленная для текущего значения Х ^к матрица Якоби (матрица из частных производных компонент вектор-функции Ф по компонентам ее аргумента), а обратной дробной чертой обозначена операция левого деления столбца на матрицу, то есть операция вычисления решения системы линейных алгебраических уравнений Ф ‘ (Х ^к ) р _к = — Ф (Х ^к ).

В рассматривамом случае в качестве начальных приближений к решению системы ( 34 ) естественно при i = 1,..., п — 1 использовать значения N 0 , вычисляемые по формуле ( 30) (для Ng и N , в силу ( 34) фактически известны точные значения), что мы и будем далее предполагать.

Для дважды непрерывно дифференцируемой функции Ф при условии невырожденности матрицы Якоби в окрестности точного решения метод Ньютона сходится весьма быстро (с квадратичной скоростью), но его сходимость носит локальный характер (требуется достаточная близость начального приближения к точному решению) [3, с. 250–251]. С целью обеспечить увеличение области сходимости метода Ньютона применяют различные его модификации, предусматривающие контроль нормы текущей невязки Ф (Х ^к ) и дробление полного шага, если на текущей итерации эта норма возрастает или жеубы-вает, но недостаточно быстро.

Изложим алгоритм к-й итерации применявшейся нами конкретной реализации одного из вариантов модификации метода Ньютона, предложенных в 1980 году О. П. Бурдаковым (см. [31] ); предполагаем, что заданы требуемая точность е решения уравнения Ф (Х) = 0 и априорная верхняя граница Н для величины шага. Алгоритм состоит из шести этапов:

• 1)    вычислить р _к = — Ф (Х ^к ) \ Ф ' (Х ^к );

• 2)    (условие останова): если || р _к ^ < е, то принять Х ^к + р _к за искомое приближенное значение точного решения и завершить итерации метода;

• 3)    положить р _к = р _к , если || р _к || 6 Н , и р _к = Нр _к / || р _к || в противном случае;

• 4)    взять i = 0;

• 5)    если || Ф (Х ^к + р> _к /2 ^г ) || 6 (1 — 1/2 ^{г +1} ) || Ф (Х ^к ) || , то перейти к следующему этапу, а иначе увеличить i на единицу и повторить данный этап;

• 6)    принять за Х ^{к +}1 ту из рассмотренных точек Х ^к + р _к /2 ^г , для которой значение нормы невязки является наименьшим, и перейти к следующей итерации.

Теперь заметим, что в рассматриваемом случае матрица Якоби является трехдиагональной и при i = 1,..., п — 1 i-е уравнение системы Ф ‘ (Х ^к ) р _к = — Ф (Х ^к ) имеет вид:

• ^c i ^p k,i - 1 ^{+ a} i ^p k,i ^{+ b} i Р к,г +1         ^E k,i ,

где E _kji — г-я компонента невязки, вычисленной в точке X ^к (то есть значение левой части г-го уравнения системы ( 34 ) при текущих значениях обратных наклонов N _i ), а c _i = д Фк дХ^ 1 , a _i = дФ _i /9N _i , b _i = дФ _i /дN _{i +1} . Явные выражения для этих коэффициентов таковы:

C i = A i N i 1 / 2 (N i ¹ / ⁴ N i ¹ - / ⁴ + N i ^{- 1} / ⁴ N i - ¹/⁴ / | A i - i | ) / 2N_ 1 , a i = 1 + ( 3A i N i ^{1 /} 4 N i ^{1 /} 1⁴ - A i N i ^{- 1 / 4} N i Z ¹/⁴ / | A i - 1 | + 1 / 4 1 / 4             - 1 / 4 - 1 / 4                  1 / 2

• ^{+ 3} ^ i ^N i    ^N i +1 ^- M i ^N i     ^N i +1 / ^{| A} i | )/ ^{2 N} i    ,

• 6.    Результаты вычислительных экспериментов

b i = M i N i ¹ / ² ( N i ¹ / ⁴ n + + N i ^{- 1} / ⁴ N i +1 / ⁴ / | A i | ) / 2N i +1 .

Мы уже отмечали, что для достаточно густой сетки нелинейные слагаемые в уравнениях для обратных наклонов малы. В этих условиях матрица коэффициентов системы Ф ‘ (X ^к ) р _к = — Ф (X ^k ) имеет выраженное диагональное преобладание. Отсюда следует [5, с. 60–62], что она заведомо невырождена, а для решения рассматриваемой системы можно эффективно использовать метод монотонной прогонки. После того, как обратные наклоны N _i будут вычислены, можно по явным формулам найти и сами наклоны m _i , и значения коэффициентов Д и ^ _i , чем и завершается процесс построения интерполяционного сплайна из множества M ^22 .

Подчеркнем отличие таких сплайнов от сплайнов из пространства P3\. Для последних уравнения для наклонов являются линейными, и решение системы линейных уравнений с трехдиагональной матрицей коэффициентов выполняется один раз; в случае же сплайнов из множества M ^2² такую систему приходится решать несколько раз — в зависимости от того, насколько быстро для конкретных данных сходится метод Ньютона и каково значение параметра е.

Теперь рассмотрим случай группы G 1s . Для нее к _s = 1; это означает, что в системе уравнений для обратных наклонов ( 26 ) 4-е и 5-е слагаемые обращаются в нуль, и непрерывность второй производной интерполяционного сплайна будет обеспечена, если в качестве обратных наклонов N _i взять значения N 0 , вычисленные в соответствии с формулой ( 30) .

Таким образом, интерполяция сплайнами из множества M ₁ ^Δ ₁ ² вообще не требует решения систем линейных уравнений (автор должен признаться, что этот результат, полученный 26 августа — через несколько дней после завершения вычислительных экспериментов со сплайнами из множества M ₁ ^Δ ₂ ² , стал для него ошарашивающим!).

В то же время нужно отметить, что с этой разновидностью интерполяционных сплайнов не все обстоит вполне благополучно. Они действительно успешно решают задачу монотонной интерполяции класса С 2 ; однако расчет наклона т 0 по любой из формул ( 27 ) — ( 29) основан на использовании всего трех значений интерполируемой функции: Y i - 1 , У ^ , Y i +i (и представляет собой модификацию интерполяции кубическими многочленами Бесселя; известно, что порядок погрешности при такой интерполяции составляет O(h 3 ), где h — максимальный шаг сетки [32, с. 50]). Интерполяция же сплайнами из пространства P ₃ ^Δ ₁ обеспечивает для достаточно гладкой интерполируемой функции порядок погрешности O(h ⁴ ) [5, с.33].

Рассмотрим результаты ряда вычислительных экспериментов по интерполированию монотонных функций сплайнами из множеств M ₁ ^Δ ₁ ² и M ₁ ^Δ ₂ ² .

Пример 1. Как и в [4] , выполним интерполирование на отрезке [0, 1] функции у = е ^{- Кх} , где К = 4, при граничных условиях типа I (начнем с числа п отрезков разбиения, равного 1, и будем последовательно сгущать используемые сетки, каждый раз деля отрезки разбиения пополам). Для сравнения приведем также результаты эрмитовой интерполяции данной функции (взятые из [4] ) и результаты интерполяции кубическими сплайнами дефекта 1.

Отметим, что интерполянты из пространств P ^2 и P ^1 сохраняют монотонность исходной функции лишь при п> 1. Что касается точности приближения, то поведение норм погрешностей таково:

п	1	2	4	8	16	32
P 3Δ2	0.119	0.0165	0.00161	0.000127	0.00000899	0.000000597
M 1Δ11	0.072	0.0133	0.00204	0.000283	0.00003741	0.000004786
M 1Δ21	0.059	0.0082	0.00080	0.000064	0.00000449	0.000000298
P 3Δ1	0.119	0.0219	0.00200	0.000149	0.00000969	0.000000621
M 1Δ12	0.072	0.0485	0.01014	0.001658	0.00023705	0.000031712
M 1Δ22	0.059	0.0071	0.00076	0.000062	0.00000442	0.000000296

Обращает на себя внимание высокая точность приближения, получаемая при выборе группы G ₂ ^s в качестве реализации группы типа G ^s .

Для оценивания скорости приближения вычислим для приведенных данных значения показателей затухания , введенных с этой целью К. Де Бором [32, с. 30] и определяемых так:

« rnn = (ln( H М) - ln( H ^е т|| )) / 1п(п/т) ,                         (37)

где || е _т || и || е _п | — значения норм погрешностей интерполяции для чисел отрезков разбиения, равных соответственно т и п. Результаты вычислений таковы:

т, п	1,2	2, 4	4, 8	8, 16	16, 32
P 3Δ2	— 4.88	— 4.55	— 4.31	— 4.17	— 4.09
M 1Δ11	— 4.16	— 3.67	— 3.36	— 3.18	— 3.10
M 1Δ21	— 4.87	— 4.55	— 4.31	— 4.17	— 4.09
P 3Δ1	— 4.18	— 4.68	— 4.46	— 4.26	— 4.14
M 1Δ12	— 0.97	— 3.06	— 3.08	— 3.06	— 3.03
M 1Δ22	— 5.22	— 4.39	— 4.26	— 4.14	— 4.08

Для сплайнов из множества M f'l² (а также для эрмитовых интерполянтов из множества M f'l 1 ) значения показателей затухания соответствуют погрешности O(h ³ ) (чего и следовало, как мы отмечали выше, ожидать), а для остальных интерполянтов — погрешности 0(^ 4 ).

Отметим также, что построение интерполянта из множества M ^2² при е = 10 ^{- 14} (это значение, использовавшееся во всех представленных здесь вычислительных экспериментах, лишь на полтора десятичных порядка больше е_маш — машинного эпсилон , служащего [3, с. 41—44] мерой относительной точности машинной арифметики; для чисел двойной точности в стандарте IEEE е_маш « 2.22 • 10 - ¹⁶ ) потребовало 4 итераций метода Ньютона при п = 2, 4, 8 и 3 итераций при п = 16, 32.

Пример 2. Рассмотрим с целью тестирования алгоритмов монотонной интерполяции следующую функцию:

/ (ж) = 4ж ⁹ — ж ⁷ + 4ж ³ — 6ж ² + 3ж. (38)

Данная функция на отрезке [ 0, 1] монотонно возрастает от 0 до 4, принимая при ж = 1 / 2 значение 1 / 2 . Ее интерполирование кубическими сплайнами представляет определенные трудности в плане обеспечения монотонности интерполянта, поскольку ее первая производная на данном отрезке изменяется резко неравномерно: при ж = 0 она принимает «умеренное» значение, равное 3, при ж = 1 / 2 — весьма малое значение, равное 1 / 32 , а при ж =1 — «большое» значение, равное 32.

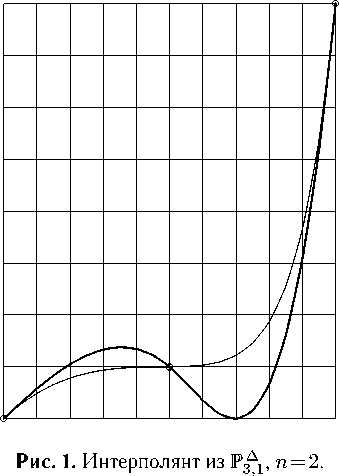
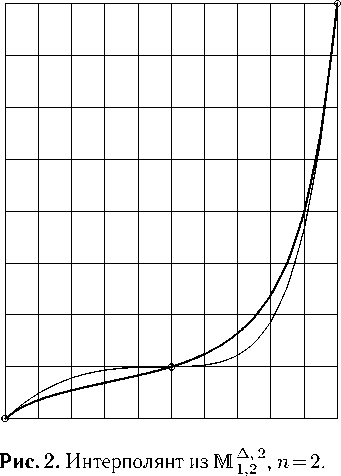
Вычислительные эксперименты по интерполированию данной функции показали, что при п = 1 и п = 2 интерполянты из пространств P3Δ2 и P3Δ1 не являются монотонными. На рисунках 1 и 2 представлены результаты интерполирования функции (38) при п = 2 сплайнами соответственно из пространства Р^ и из множества M ^22 (тонкая линия отвечает интерполируемой функции, более толстая — интерполянту).

Нормы погрешностей ведут себя так:

п	1	2	4	8	16	32	64
P 3Δ2	2.25	0.48	0.059	0.0052	0.00038	0.000026	0.00000168
M 1Δ11	0.91	1.31	0.105	0.0127	0.00159	0.000199	0.00002466
M 1Δ21	1.01	1.18	0.076	0.0061	0.00044	0.000030	0.00000193
P 3Δ1	2.25	0.65	0.079	0.0062	0.00042	0.000027	0.00000172
M 1Δ12	0.91	0.49	0.394	0.0644	0.00939	0.001267	0.00016284
M 1Δ22	1.01	0.26	0.198	0.0116	0.00040	0.000028	0.00000188

В данном случае интерполянты из множеств M ₁ ^Δ ₂ ¹ и M ₁ ^Δ ₂ ² практически не уступают по точности приближения интерполяционным кубическим сплайнам. Показатели затухания а _ттг при этом принимают такие значения:

т, п	1,2	2, 4	4, 8	8, 16	16, 32	32, 64
P 3Δ2	- 3.79	- 4.11	- 4.15	- 4.10	- 4.06	- 4.03
M 1Δ11	0.90	- 4.94	- 3.60	- 3.27	- 3.13	- 3.08
M 1Δ21	0.40	- 5.37	- 4.29	- 4.13	- 4.07	- 4.04
P 3Δ1	- 3.06	- 4.13	- 4.33	- 4.23	- 4.13	- 4.07
M 1Δ12	- 1.55	- 0.42	- 3.08	- 3.03	- 3.02	- 3.03
M 1Δ22	- 3.36	- 0.53	- 4.82	- 5.30	- 3.99	- 4.00

Вновь для интерполянтов из множеств M ₁ ^Δ ₁ ¹ и M ₁ ^Δ ₁ ² значения показателей затухания соответствуют погрешности O(h 3 ), а для остальных интерполянтов — погрешности O(h 4 ). Построение интерполян-та из множества M ₁ ^Δ ₂ ² во всех случаях потребовало 5 итераций метода Ньютона.

Пример 3. Рассмотрим следующий набор данных, взятый из работы [16] :

Х _г  1000  1250  1500  1920  1960  1980  1990  2000  2005  2011

Х_г   0.31   0.40   0.50   1.86   3.02   4.44   5.27   6.06   6.45   7.02

Здесь представлены значения численности населения земного шара (млрд человек) с 1000 по 2011 год по оценкам Бюро переписи населения США (United States Census Bureau, USCB). Эти данные являются строго монотонными, и при их интерполировании естественно, как отмечается в [16] , потребовать строгой монотонности и от интерполянта.

На рисунке 3 видно, что интерполяционный сплайн из пространства Р-^, построенный для этих данных, монотонным не является.

В то же время (Рис. 4) интерполянт из множества M ^ 2 ² (его построение потребовало 5 итераций метода Ньютона) сохраняет монотонность. В обоих случаях для задания значений производных в узлах Х 0 и Х 9 использовалась линейная интерполяция по двум узлам (характер данных это допускает).

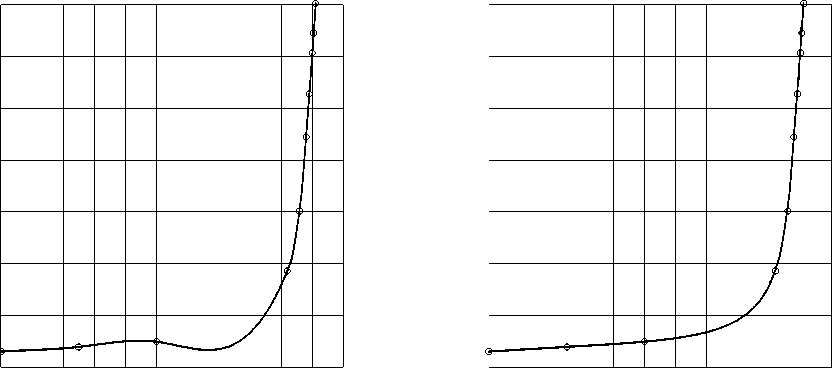
Рис. 3. Данные из [16] : интерполянт из P ₃ ^Δ ₁ Рис. 4. Данные из [16] : интерполянт из M ₁ ^Δ ₂ ²

В работе [16] эти данные интерполировались рациональными сплайнами класса С ² с двумя свободными параметрами, выбираемыми эмпирически. Построенные интерполянты также сохраняли монотонность данных, однако представленный на рисунке 4 график является более плавным; на приведенных же в [16] графиках интерполянтов на отрезке [Х ₃ , Х ₄ ] (то есть между 1920 и 1960 годом) заметна точка перегиба. Согласно [32, с. 229], точка перегиба на отрезке [Х _г , Х _{г +1} ] — чужеродная , если величины ⁵ г = ^Д г ^{— Д} г - 1 ^{и 5} г +1 = Д _г +1 — Д _г имеют одинаковый знак; в нашем же случае 5 3 « 0.026 и 5 4 « 0.042, так что упомянутая точка перегиба действительно является чужеродной.

Интерполирование этих же данных сплайнами из множества M ₁ ^Δ ₁ ² дало результат, мало отличающийся от представленного на рисунке 4. Максимальное различие между обоими интерполянтами на всем отрезке [Х ₀ , Х ₉ ] составляло менее 2 %.

Заметим также, что при построении интерполянтов из множества M ₁ ^Δ ₂ ² во всех выполненных вычислительных экспериментах метод Ньютона сходился без каких-либо осложнений, и на всех итерациях шаги метода были полными.

• 7.    Заключение

В данной работе для сплайн-интерполянтов, построенных с использованием однопараметрических групп диффеоморфизмов единичного отрезка [0, 1] и сохраняющих при строго монотонных исходных данных свойство строгой монотонности, предложены способы обеспечения гладкости класса С ² для получаемого интерполянта. Обсуждаются свойства интерполянтов предложенного вида. Приведены результаты ряда вычислительных экспериментов, подтвердивших эффективность предложенного подхода.