Морские течения и гравитомагнетизм

Выделяют три группы течений, различающиеся теми факторами, которые создают эти течения: [1]

• •    Градиентные течения, вызванные горизонтальными градиентами гидростатического давления,

• •    Течения, вызванные ветром

• •    Приливные течения,

Эти факторы могут служить причиной возникновения течений, но не могут поддерживать существование (в течении столетий) замкнутой траектории течения (поскольку противоположно направленные участки этой траектории должны подвергаться противоположно направленным воздействиям, а указанные факторы однонаправлены во всех точках траектории). Однако течения, как правило, являются замкнутыми (как можно видеть на картах – см.

рис. 1, 2 [1]). Следовательно, должны существовать внутренние массовые силы, создающие течение.

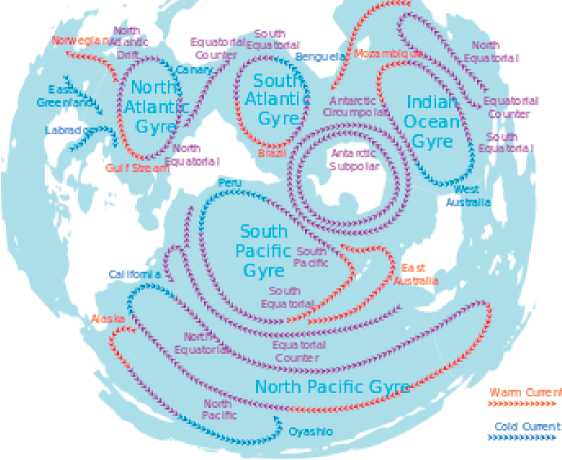
Рис. 1.

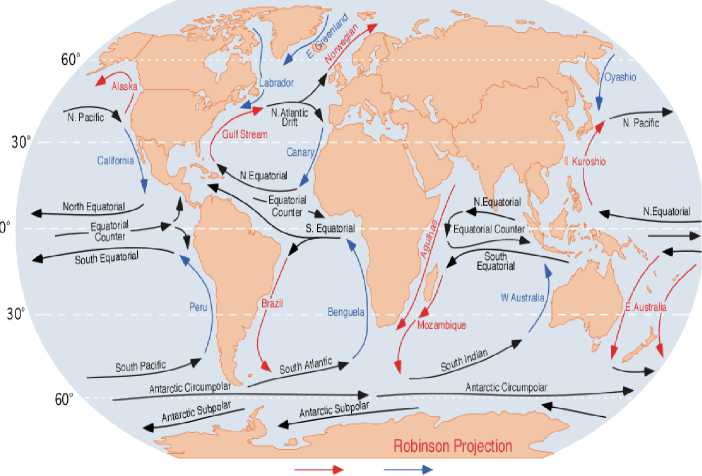
Warm Current Cold Current

Рис. 2.

Течения сохраняют конфигурацию своей траектории и форму сечения струи. Для объяснения этих явлений обычно указывают на отличия в составе и свойствах вод струи и окружающих вод. Естественнее (на наш взгляд) предположить, что эти отличия являются следствием обособленности струи, а не причиной этой обособленности. Следовательно, должны существовать силы, обеспечивающие устойчивость конфигурации и формы сечения струи.

Насколько известно автору, такие вопросы не отражены в существующих теориях и численных методах расчета океанских течений – см., например, [2, 3]. Ниже предлагается теория, объясняющая существование внутренних движущих сил и сил, обеспечивающих устойчивость течения.

Ранее автор предложил математическую модель водоворота [4]. При этом использовались уравнения гравитомагнетизма – уравнения, подобные уравнениям Максвелла для электродинамики -максвеллоподобные уравнения гравитации (далее – МПГ-уравнения). Взаимодействие между движущимися массами воды описывалось гравитомагнитными силами Лоренца (далее ГЛ-силы), аналогичными силам Лоренца в электродинамике [5]. Дальнейшие рассуждения аналогичны приведенным в [4], где, в частности, показано, что ГЛ-силы имеют значительную величину.

2.    Основная математическая модель

МПГ-уравнения для гравитомагнитных напряженностей H и плотностей массовых токов J в стационарном гравитомагнитном поле имеют вид:

div(H )= 0,(1)

rot(H) = J ,(2)

div( J) = 0,(3)

Рассмотрим течение в форме параллелепипеда, где ав - уровень водной поверхности, а оси расположены в соответствии с рис. 3.

Будем полагать, что скорость v течения направлена вдоль оси ох . В декартовых координатах уравнения (1, 2, 3) примут вид:

5Hz _^Hy = J

5y     dz     '

5Hx-^ = J

5z     5x     y ’

5Hy 5Hx = J

5x     5y     z ’

5Hx 5Hy Qh x + y + z = 0,

5x 5y 5z

5J_x 5J_y 5 J

• x. ₊ y ₊    z. = о .

5x   5y   5z

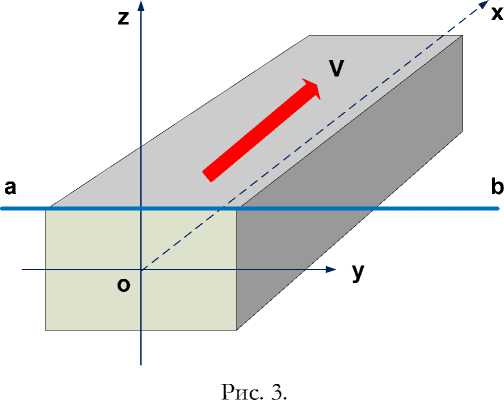
Из физических соображений ясно, что поле должно быть однородным вдоль оси ОХ, т.е. должны отсутствовать производные по аргументу x, и, следовательно, уравнения (5-9) должны быть переписаны в виде:

^ H^ -^ H y = Jx ,                         (10) x 5 y     5 z 5HT = J y ,                               (H) 5 z -^ H x = J z >                              (12) 5 y 5H QH —+ — z- = 0 ,                         (13) 5 y     5 z

J ^д = 0 .

dy

Решение этой системы уравнений может иметь следующий вид (что можно проверить непосредственной подстановкой):

Hx. = П- f2(y) • exp(n- z) ,(15)

Hy. = n f8(y) • exP(nz),(16)

Hz. = - f8'( y) • exp(nz),(17)

Jx. = n2f7(y) • exp(n z) ,(18)

J. = n2f2(y) • exP(nz),(19)

Jz = -n • f(y) • exp(n •z),(20)

где

^f 2⁽ y ) = sin ( b 3 y ) ( b l + b 2 y ⁴ ),

f 2 ‘ ( y ) =

b з cos ( b₃ y )/ b i + b _г y ⁴ )-

^{- 4 b} 2 y ³ sin ^{( b} 3 y )/ ( b l + ^b 2 y ⁴ )

f 7(y ) = b4 ,(23)

f 8(y) = exp(b5| y I) - b4 ,(24)

f8 (y) = b5 exp(b5 1 y |) ,(25)

• П, b1^₅— некоторые константы, причем

4. Анализ решения

Ь5 = -(П )(26)

Далее мы рассмотрим указанные функции при n = 0.2, b 1 = 3, b ₂ = 0.0016, b ₃ = 0.06, b ₄ = 4 .

Массовые токи J_x , J_y , J_z , не зависят от координаты х, а в зависимости от координаты у , определяются по (18-20). При этом ток J_x не зависит от у (см. (18, 23)), а вид функций (19, 20) показан на рис. 4 – см. также (21, 22).

На рис. 5 показаны массовые токи J_x , J_z , как функции координаты z . Показаны токи J_z при нескольких определенных значениях у и только одна функция тока J_x , поскольку этот ток не зависит от у .

Рассмотрим векторное поле токов J y , J z в вертикальной плоскости сечения струи. На рис. 6 представлен фрагмент этого поля у = - 15, 15 и z = [0, - 2, - 4, - 6, - 8] . Таким образом, массовые токи в струе циркулируют по вертикали. При этом в малой центральной области масса воды с большой скоростью опускается вниз, а в отдаленной, но значительной по объему области, с малой скоростью поднимается вверх. На свободной поверхности струи вдоль оси образуется углубление (см. дугу АА на рис. 6), а вдоль границ образуется возвышение (см. дуги АВ на рис. 6). Это аналогично поверхности водоворота. Вода с возвышения устремляется в углубление. Кинетическая энергия такой циркуляции расходуется только на потери от внутреннего трения. Потенциальная энергия водоворота не изменяется. Т.е. в этом случае нет преобразования потенциальной энергии в кинетическую и обратно. Однако (как указывалось в [4]) гравитирующее тело расходует свою энергию на создание и поддержание массовых токов.

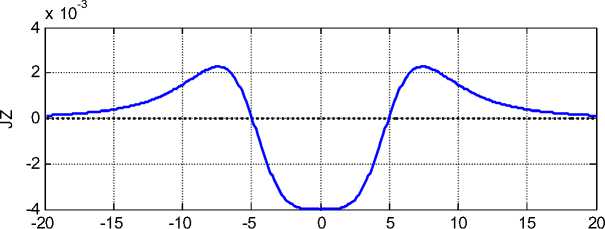
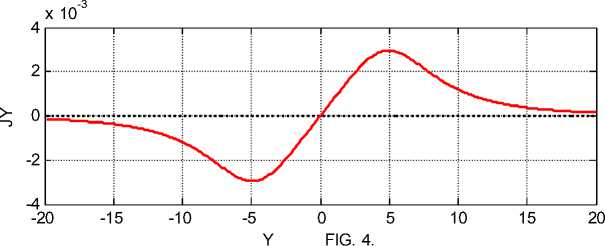
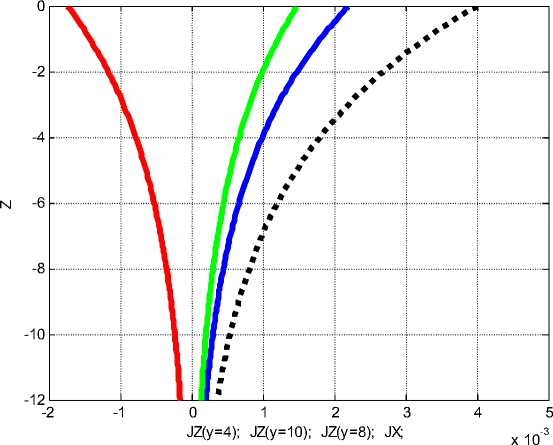
Рис. 5.

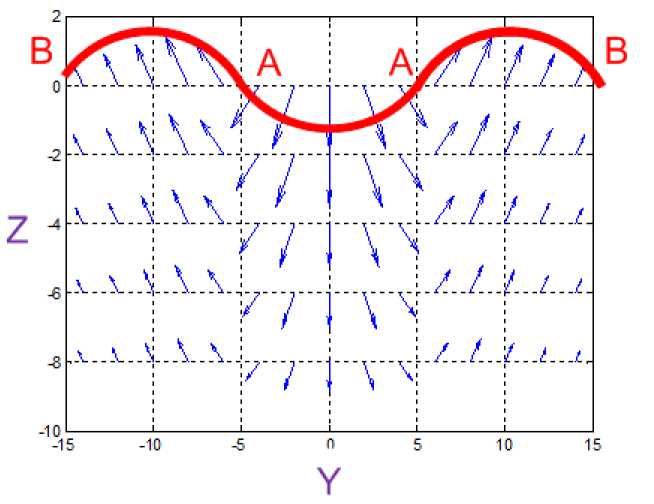
Рис. 6.

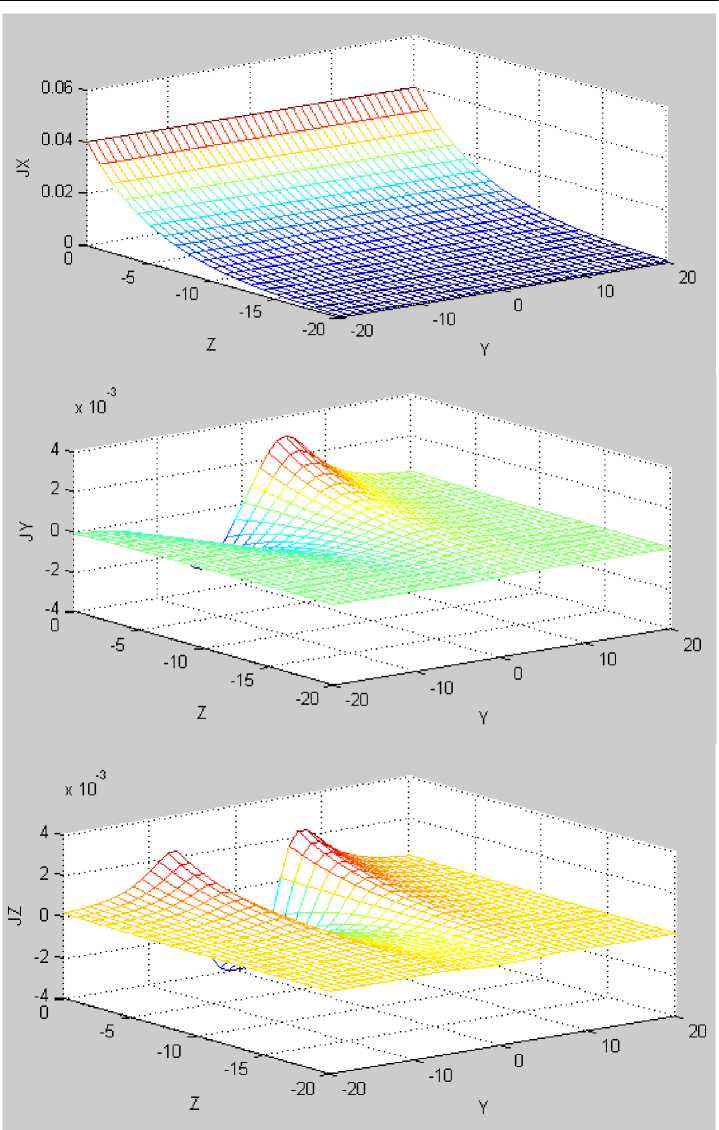
Рис. 7.

На рис. 7 показаны токи J x , J y , J_z на плоскости сечения струи. Видно, что токи J_y , направленные перпендикулярно боковой поверхности струи, близки к нулю на боковой поверхности и направлены из струи (см. также рис. 4). Это означает, что боковые воды не входят в струю, а воды струи не выходят из струи, т.е. нет обмена между водами струи и окружающими водами: струя сохраняет свой состав!

Видно, что токи Jx сохраняют свою величину на протяжении всего течения, но быстро уменьшаются с глубиной. Это соответствует, например, структуре Гольфстрима [6]. Вертикальные токи Jz также уменьшаются вертикальном размере течения.

-4

x 10 ⁴

с

глубиной и

можно

говорить о

-5 0

-з x 103

от

-20

Y

-4 0

Z -20

-20 Y

-10

Z -20

-0.005 от

-0.01

0.01

0.005

Z -20

-20

Y

Рис. 8.

Z -20

-20

Y

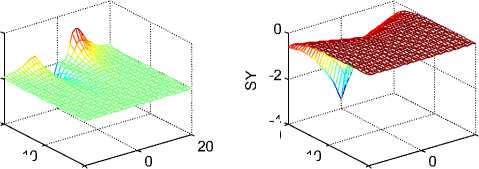
По аналогии с [7] запишем выражение для проекций вектора плотности гравитационной энергии:

^S xyz

Sx = JyHz Sy = JzHx , Sz = JxHy

^^^^^^^

^^^^^^в

J z H y

J x H z

^^^^^^в

J y H x

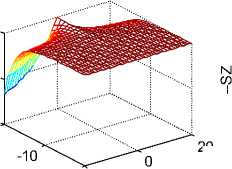
На рис. 8 показаны плотности потоков энергии

S x , S y , S_z, ( — S_z ) на плоскости сечения струи.