Multi Population Hybrid Genetic Algorithms for University Course Timetabling Problem
Автор: Meysam Shahvali Kohshori, Dariush Zeynolabedini, Mehrnaz Shirani Liri, Leila Jadidi
Журнал: International Journal of Information Technology and Computer Science(IJITCS) @ijitcs
Статья в выпуске: 6 Vol. 4, 2012 года.
Бесплатный доступ
University course timetabling is one of the important and time consuming issues that each University is involved with it at the beginning of each. This problem is in class of NP-hard problem and is very difficult to solve by classic algorithms. Therefore optimization techniques are used to solve them and produce optimal or near optimal feasible solutions instead of exact solutions. Genetic algorithms, because of multidirectional search property of them, are considered as an efficient approach for solving this type of problems. In this paper three new hybrid genetic algorithms for solving the university course timetabling problem (UCTP) are proposed: FGARI, FGASA and FGATS. In proposed algorithms, fuzzy logic is used to measure violation of soft constraints in fitness function to deal with inherent uncertainly and vagueness involved in real life data. Also, randomized iterative local search, simulated annealing and tabu search are applied, respectively, to improve exploitive search ability and prevent genetic algorithm to be trapped in local optimum. The experimental results indicate that the proposed algorithms are able to produce promising results for the UCTP.
University course timetabling problem(UCTP), genetic algorithm, fuzzy logic, local search, heurestic
Короткий адрес: https://sciup.org/15011694
IDR: 15011694
Текст научной статьи Multi Population Hybrid Genetic Algorithms for University Course Timetabling Problem
Published Online June 2012 in MECS
University course timetabling problem is difficult task faced by educational institutions. Solving a real world university timetabling problem manually often requires a large amount of time and expensive resources [1-7]. In order to handle the complexity of the problems and to provide automated support for human timetables, much research in this area has been invested over the years [3].The university course timetabling problem involves the scheduling of classes, students, teachers and rooms at a fixed number of timeslots, in a way that satisfies a set of set of constraints, which often makes the problem very hard to solve in real world circumstances [3-4].In brief there are two prominent representative instances of the UCTP problem: Curriculum based course timetabling and post enrollment course timetabling, both types of problems have been frequently solved in the past, as evidenced by many surveys [4-6]. In curriculum based timetabling, conflicts between courses are determined by the curricula published by the University. Conflicts in post enrollment timetabling are established directly by students who individually enroll into particular courses. It is very difficult to find a general and effective solution for timetabling due to the diversity of the problem, the variance of constraints, and particular requirements from university to university according to the characteristics. There is no known deterministic polynomial time algorithm for the UCTP, since it is an NP-hard combinatorial optimization problem [3] [8].
Constraints in UCTP can usually be divided into two types [1-4][9]:
-
• Hard constraints have to be satisfied under any circumstances. For example, only one course can be scheduled in rooms at any time slot. Timetables with no violations of hard constraints are called feasible solutions.
-
• Soft constraints need to be satisfied as much as possible. For example, number of course for each group should not go over two per day. Due to the complexity of the real-world timetabling problem, the soft constraints may need to be relaxed since it is not usually possible to generate solutions without violating some of
them. Soft constraints are usually used within the cost evaluation function to evaluate how good the solutions are.
A wide variety of papers, from the fields of operational research and artificial intelligence, have addressed the broad spectrum of university timetabling problems [11]. Early timetabling research focused on sequential heuristics which represented a simpler and easier method for solving graph coloring problems, the principle idea being to schedule events one by one starting with the most difficult first [12-13].Researchers have proposed various timetabling approaches by using constraint-based methods, graph-based approaches, cluster-based methods, population-based approaches, meta-heuristic methods, multi-criteria approaches, hyper-heuristic/self-adaptive approaches, case-based reasoning, knowledge-based and fuzzy-based approaches. A comprehensive review and recent research directions in timetabling can be found in [5], [10], and [14]. GAshave been used to solve the UCTP in the literature [5], [9], [15]. Rossi-Doria et al. [16] compared different meta-heuristics to solve the UCTP. They concluded thatconventional GAs do not give good results among a number ofapproaches developed for the UCTP. Hence, conventional GAsneed to be enhanced to solve the UCTP.
Population-based algorithms, particularlygenetic algorithmshave been themost commonsolutionin recent yearsfor UCTP. Therefore,inthis paper three algorithmsbased ongenetic algorithmare presented: FGARI, FGATS andFGASA.In proposed algorithms, fuzzy logic is used to measure violation of soft constraints in fitness function to deal with inherent uncertainly and vagueness involved in real life data. Also, randomized iterative local search, simulated annealing and tabu search are applied, respectively, to improve exploitive search ability and prevent genetic algorithm to be trapped in local optimum.
The rest of this paper is organized as follows. Section IIbriefly describes related work on the UCTP. The UCTP studied in this paper is described in Section III. Section IV presents theproposed methods in this paper. Experimental results the sensitivityanalysis of key parameters and comparing the proposedGAs with constructive algorithms of them are reported and discussed in Section V. Finally, Section VI concludes this paper with some discussions on the future work.
-
II. Related Works
Several algorithms have been suggested to solve timetabling Problems. The first set of algorithms is based on graph coloring heuristics. These algorithms show a great efficiency in small instances of timetabling problems, but are not efficient in large instances. Then, random search techniques, such as genetic algorithms (GA), simulated annealing (SA), tabusearch (TS), etc., were introduced to solve timetabling problems [2] [5] [17].
In general, there are two types of meta-heuristics algorithms [5]. The first type is the local area search – based algorithms and the second type are populationbased algorithms. Each type has some advantages and disadvantages. Local area-based algorithms areSA [18], a very large neighborhood search [1], TS [19], and many more. Usually, local area-based algorithms focus on the exploitation rather than exploration, which means that they move in one direction without performing a wider scan of the search space.. Population-based algorithms start with a number of solutions and refining them to obtain global optimal solution (s) inthewhole search space. Population based algorithms that are commonly used to deal with the timetabling problems are evolutionary algorithms(EAS) [20] particle swarm optimization [19], colony ANT – Optimization[21], artificial immune system [16] [20], etc.
In recent years, several researchers have used GAs forUCTP. They increased the efficiency of Gas using modified genetic operators and techniques LS [22].In general, when a simple GA is applied, it may produce illegal timetables that have duplication and / or missing events. Quality of solutions produced by populationbased algorithms may not be better than the local areabased algorithms mainly due to the fact that populationbased algorithms are more concerned with exploration than exploitation [5] [23].Population-based algorithm scans solutions in the entire search space without concentrating on the individuals of good fitness within a population. In addition, population-based algorithms may experience premature convergence, which may lead to them being trapped into local optima. Other drawback of these algorithms is requiring more time [24]. However, Gashave several advantages when compared to other optimization techniques [25]. For example, although the GAs can perform a multidirectional search using a set of candidate solutions [26].Different combinations of local and global based algorithms has been reported to solve problems in the timetabling literature [16] [20], [27]. In addition, it is also being increasingly realized that EAs without incorporation of problem specific knowledge do not perform as well as mathematical programmingbased algorithms on certain classes of timetabling problems [28]. In this paper, we want to combine the good properties of local- and global-area-based algorithms to solve the UCTP. We try to make a balance between the exploration ability (global improvement) of GAs and exploitation ability (local improvement) of LS. In addition, an external memory data structure is introduced to store parts of previous good solutions and reintroduce these stored parts into offspring in order to enable the proposed GAs to quickly locate the optimum of a UCTP.
-
III. Problem Defenition
Description of UCTP in this paper is based curriculum that generally is used in Iran. The problem consists of the following entities:
Days and timeslots: A certain number of working days per week are considered. In this paper, the number of working days is assumed 5. Each day is divided into a fixed number of timeslots, which are the same for all days. Here the number of timeslots per day is considered 9, that each of them is one hour. Therefore, the total number of timeslots is 45. Timeslots are numbered from1 to 45 as in many studies is used [3] [5] [20]. In this paper timeslots are displayed by set T = {tl, t2 , ■”,t4 5} ■
Subjects: Defines the set of course topics.
Rooms: Each room has a capacity, expressed in terms of number of available seats, and special facilities.
Curricula: A curriculum is a group of courses such that any pair of courses in the group has students in common. The main feature of courses in the same curriculumis that they should not overlap.
Professors: Each professor has a specific timetable for his/her presence in the University and specializes in offering certain subjects.
Courses: Each course has a fixed period of time and is related to the particular subject and requires that is held in room with particular capacity and facilities.
According to above entities, UCTP is allocation of timeslot, professor and the room to set of courses so that all desired hard constraints are met and soft constraints are satisfied as far as possible.
Hard constraints that must be satisfied in order to keep the timetable feasible are the following:
-
1. Courses in each curriculum must not have overlap.
-
2. Each room must not have more than one course in a specific timeslot.
-
3. Each professor must not be assigned to more than one room in a specific timeslot.
-
4. Each professor must only teach at days he/she is available at university.
-
5. A class that is assigned to a course must have facilities and capacity that the course need.
Soft constraints that should be satisfied in order the timetable to be considered of high quality are the following:
-
1. Each course is assigned to a professor that it is in his area of expertise.
-
2. Timetable of each professor should be same as the timetable that presented by professor.
-
3. Minimum and maximum number of hours of attendance of each student per day is satisfied.
-
4. Lectures belonging to a curriculum should be adjacent to each other.
-
5. A class hasn’t scheduled in the last timeslots of a day.
-
6. Minimum and maximum number of hours of attendance of each professor is satisfied.
-
7. Student presence in consecutive hours per day.
-
IV. Proposed Algorithms
In this paper three hybrid genetic algorithms are proposed, FGARI, FGASA and FGATS that are combination of genetic algorithm, fuzzy logic and local search algorithms. The difference between these algorithms is in local search algorithm of them.Infact, these algorithms are modified genetic algorithms that general pseudo-code of them has shown in figure 1.
We use the steady state genetic algorithm model as mentioned in [11], where only one child solution is generated with selection, crossover and mutation at each generation. The child then will be improved by local search. In the end, the worst population member is replaced with the new child individual. The main components of these algorithms are described in following subsections.
Initialize population
Calculate fitness of all solutions
Sort population by fitness
While termination condition not reached do
Select two parents from population by tournament selection with size 2
Create child solution using crossover with a probability- Pc
Apply mutation with a probability Pm to child solution
Apply Local Search to child solution
Replace child solution with the worst member of the population
Sort population by fitness
End while
The best solution achieved as output
Figure 1: General pseudo-code of proposed algorithms
-
A. Chromosome Representation
Encoding of chromosomes for GA model is an essentialfactor in success of a GA as it will affect not only theefficiency and performance of GA but also the speed andquality of final result.
In this paper a chromosome is represented as a 3 X Nc matrix, where CCc is number of courses. The index of columnsis the identification number of a course and content of rows ofthe matrix shows identification number of the instructor, starttimeslot and room successively. Figure 2 shows thestructure of a chromosome.
|
Ci |
Ca |
C, |
|||
|
Professor ID |
1 |
3 |
1 |
||
|
Start Timeslot ID |
23 |
12 |
30 |
||
|
Room ID |
10 |
2 |
10 |
Figure 2: Chromosome structure
-
B. Initial population
The initial population is generated so that the random properties of solutions are preserved and all hard constraints are satisfied too.
For this purpose, using the inputs of UCTP a professor-course matrix, a conflict-course matrix and a room-course matrix, a professor-timeslot matrix and room-timeslot matrix are generated.
A professor-course matrix is a Np × Nc matrix where each element in the matrix is represented by “0”, “1” or “2”. The value “0” shows that the professor cannot teach the course. The value “1” shows that the professor can teach the lesson but not expert in that course. The value “2” chows that the professor is expert in the course. Np and Nc show number of professors and number of courses respectively.
A conflict-course matrix is a Nc × Nc matrix where each element in the matrix is represented by “0” or “1. The value “0” shows that the courses have no conflict. The value “1” shows that the courses haveconflict.
A room-course matrix is a Nr × Nc matrix where each element in the matrix is represented by “0” or “1. The value “0” shows that the room is not suitable for the course. The value “1” shows that the room is suitable for the course. Nr shows number of rooms.
A professor-timeslot matrix is a Np × 45 matrix where each element in the matrix is represented by “0”, “1” or “2”. The value “0”showsthat the professor don’t attend at university. The value “1” shows that the professor attends in university but don’t desire to teach in that timeslot. The value “2” shows that the professor attends in university and desire to teach in that timeslot.
A room-timeslot matrix is a Nr × 45 matrix where each element in the matrix is represented by “0” or “1” The value “0” shows that the room is empty in the timeslot. The value “1” is not empty in the timeslot.
After defining these matrixes, courses sorted according to the number of professors that can teach them in ascending order. Then for each course are randomly selected professor, timeslot and room, respectively, so that all hard constraints are satisfied, and as follows:
-
1. Select a professor based on professor-course matrix.
-
2. Select a suitable timeslot between the timeslots of the selected professor form step 1 using professortimeslot matrix.
-
3. Select a suitable room according to room-timeslot matrix androom-course matrix.
-
C. Fitness Function
Fitness of a solution depends on the satisfying of the hard and soft constraints. In these algorithms the initial population, genetic operators and local search algorithms have defined so that all hard constraints of the all solutions satisfied. Therefore, the fitness function is depended only on meeting soft constraints.So, the fitness function is addressed only by the softconstraints.On the other hand,the soft constraints are somewhat qualitative, it is vague and difficult to measure them accurately and there are some if-then relationships between them, which can describe easily fuzzy rules. Then, we use fuzzy logic for measuring soft constrains and define proper member function for each soft constraint. The fitness function is defined as follow:
Fitness function ( I )
= ∑ Wi^ ̃ (1)
1=1
Where µ ̃ shows the value of member function of i soft constraint that has a value in range [0,1] , and wi shows the weight of i th soft constraint that is assumed 100 in this paper for all soft constraints. Therefore the worst value for fitness of a solution is 700.
-
D. Selection
In proposed algorithms, tournament selection is used. In this method, 2 solutions are selected randomly by roulette wheel. Then best solution between them is selected. The selection process is applied twice at each generation to select two parents for reproduction.
-
E. Crossover
Generally, it has been shown that the uniform crossover is more effective for many problems especially for numerical optimization problems [9] [29]. In this paper a uniform crossover operator is used with a probability Pc .Finally, if the child had violation of hard constraints; we use a repair function to improve it if possible. Otherwise crossover operation is repeated.
-
F. Mutation
In this paper random is used with a probability ^m . It randomly selects a proper timeslot randomly for subject according to course-timeslot matrix. If the course had violation of hard constraints, we use a repair function to improve it if possible. Otherwise crossover operation is repeated.
-
G. Local Search Algorithms
Three local search algorithms have been presented in this paper that based of them three hybrid genetic algorithms have been proposed. All three local search algorithms act based on following neighborhood structures:
N^ : select a professor at random and swap the timeslot of two courses that related to that professor so that hard constraints are not violated.
N 2 : Choose a single course at random and move it to another random feasible timeslot.
N 2 : select a course at random and change professor. If it is necessary change timeslot and room receptively.
N 4 : select a course randomly, and then select a course that has same length and subject with that. Finally swap timeslot of them.
Randomized Iterative local search
This algorithm is used in FGARIalgorithm. Ineach iteration of this algorithm a list with K element of neighborhood structures, which mentioned above, is generated randomly. The all neighborhoods are applied to main solution and fitness of that is measured for each neighborhood. Best solution is compared with main solution. If the best solution was better than the main solution, the main solution is replaced with best solution. Otherwise the main solution is replaced with best solution with a very low probability to prevent local optima. Pseudo-code of this algorithm is shown in figure 3.
Calculate initial fitness for S, Fitness functions)
Set best solution S^ <-S
While (not termination criterion)
Create neighborhood structure list randomly, ListBS = [A^, N2,.-,Nt] For i=l: K, where К is the total number of neighborhood structures
Apply neighborhood structure i to S. NewS,
Calculate fimess forNewSj, Fitness function(NewSj)
End for:
Identify the best solution among all the NewSj wherei E [1,..., K}, NewSBa3t If (Fitness function(NewSBsst) < Fitness function^^))
S ь NewSBa3t
SbM<- NewSBast
Else
-
8 = Fitness function(NewSBast) - Fitness function(S) Generate a random number in [0,1], R If(R
6) ' '
S <- NewS^
End if
End if
End while
-
Figure 3: Pseudo-code of randomized iterative local search algorithm
Simulated annealing algorithm
Simulated annealing algorithm is used in FGASA as local search algorithm. Simulated annealing is very sensitive to its parameters and approaches that used for determine this parameter is very important. Some of the most important of these parameters are initial temperature, final temperature and cooling method.
In this paper, to determine the initial temperature To , 100 new solutions are produced through the neighborhood structures, and then the maximum difference between the fitness of two consecutive solutions is considered as the initial temperature. The final temperature ту is assumed0.09 To . The cooling function according to the method that proposed in [14] is as follow:
= 1+ ^Tr
Where Tr shows the current temperature and p is a fixed value that is assumed 0.1 in this paper.
This algorithm is iterated once at each temperature.
Pseudo-code of this algorithm is shown in figure 4.
Calculate initial fitness for S, Fitness /unction(S)
Set best solution ^g^ <- S
Create a neighborhood structure list of 100 elements randomly, ListNSlm
Create 100 solution using iistM100, Sjti = 1...100
CalculateFitness function (SJ, f,, i = 1...100
To = max(A/j)
Tf = О.О9Го
Тт = Т0
While (not termination criterion)
Create neighborhood structure list randomly, ListNS = (NpN^... ,Nk]
For i=l: K, where К is the total number of neighborhood structures Apply neighborhood structure iV,- to S, SNew
End for:
If (Fitness function (S^^ < Fitness function(SlleBt))
S *“ Siew
^best ^New
Else
6 = Fitness function(New-SBest) - Fitness function(S)
Generate a random number in [0,1], R
-6
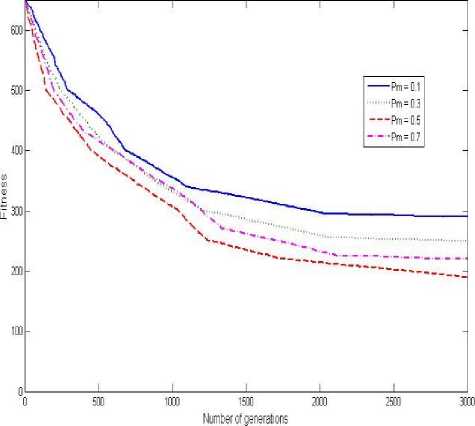
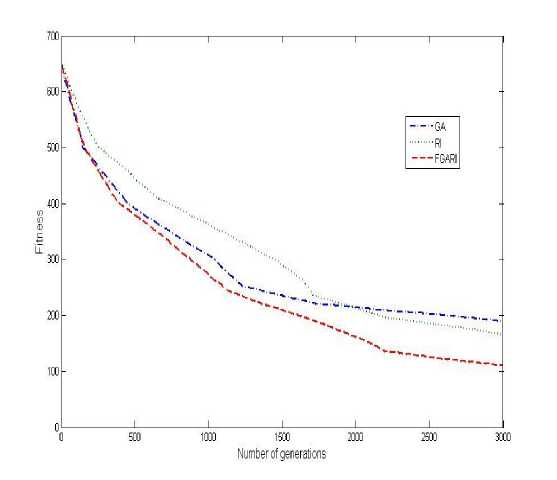
If(R 3 ^New End if End if T, Тт= 1+ Дгг End while Figure 4: Pseudo-code of simulated annealing algorithm Tabu search algorithm Tabu search algorithm is used in FGATS. The newly visited neighborhood lists are added into the tabu list (which has a fixed length). In this algorithm,a list with K element of neighborhood structures is generated randomly.Each neighborhood in the list is applied Ltimes to main solution consequently. Then thefitness of the new solution is measured. New solution is compared with main solution. If the new solution was better than the main solution, the main solution is replaced with new solution. Otherwise the main solution is replaced with new solution with a very low probability to prevent local optima. Finally the neighborhood list is added into tabu list. Pseudo-code of this algorithm is shown in figure 5. Calculate initial fitness for S, Fitness function(S) Set best solution S^ <- S While (not termination criterion) Create neighborhood structure list randomly, ListNS = {Я,,N,, .-.N^ For i=l: K, where К is the total number of neighborhood structures Apply neighborhood structure^ to S for L times, SMe„ End for: If (Fitness function (SNew) < Fitness functton(SbeBI)) *“ Siew Sept ^" Slew Else S = Fitness function(NewSgg3t) - Fitness function(S) Generate a random number in [0,1], R If(R«5) " " 8 *“ Siew End if End if Remove the first item from tabulist ifitis full Add ListNS to end of tabu list End while Figure 5: Pseudo-code of tabu search algorithm were proposed in the website of the second international timetabling competition [30] for the timetabling competition. These datasets are somewhat near to many of the real-world problem constraints and consistent with the educational system of Iran. Table 1 presents the data of these datasets in that were classified in nine different groups. Also, Table 2 demonstrates the values of proposed algorithm parameters that had been used in simulations. The values of these parameters have been determined experimentally and using the experiences of previous researchers in context the university courses timetabling. Two sets of experiments were carried out in this study. The first set of experiments are devoted to analyze the sensitivity of parameters for the performance of GA for the UCTP. The second set of experiments compare the performance of investigated GAs with or without the local search strategy on the test UCTPs. For both sets of experiments, there were 5 runs of each algorithm on each dataset and average values are used. Multi population version of proposed algorithm In order to reduce the required time for solving UCTP multi population version of proposed algorithm is expressed. In this paper two-population version is assumed. In this method genetic algorithm has been divided into two genetic algorithms with two small populations instead of one algorithm with a large population. These two algorithms run in parallel. Because diversity withinthe small populations such asalargepopulationis preserved, generated child in each generation are exchanged with each other. Pseudo code of multi population version proposed genetic algorithm is shown in figure6. For each Population i do in parallel, i=l, 2 Initialize population i Calculate fitness of all solutions Sort population i by fitness While termination condition not reached do Select two parents from population i by tournament selection with size 2 Create child solution using crossover with a probability Pc Apply mutation with a probability Pm to child solution Apply Local Search to child solution Swap generated child in populations with each other Replace child solution with the worst member of the population i Sort population i by fitness End while The best solution between populations achieved as output Figure 6 The Pseudo code of multi population version of proposed GA. V. Experimental Results In this section, we experimentally investigate the performance of the proposed methods FGARI, FGASA, and FGATS using an exhaustive simulation. The performance of these algorithms is measured in terms of best fitness and execution time. All algorithms were coded in MATLAB. All the simulations presented in this section have been conducted on datasets, which Table 1:Dataset properties Dataset number Average number of courses Average number of rooms Average number of professors 1 30 5 6 2 70 9 13 3 100 12 17 4 150 21 28 5 200 21 32 6 250 27 37 7 300 28 45 8 350 33 53 9 400 35 60 Table 2: Parameter settings in proposed algorithms Parameter Value Crossover probability 0.8 Mutation probability 0.5 Population size 100 Tabu list size 9 Neighborhood structures list size in FGARI and FGASA 9 Neighborhood structures list size in FGATS 3 L parameter in FGATS 3 Maximum number of generation 4000 Maximum number of iteration in local search algorithms Three times the numberof courses Average number of courses 200 A. Evaluation the effect of crossover probability parameter on proposed GA Performance of in genetic algorithm is very sensitive to crossover probability (PQ) parameter. To assess the impact of this parameter, the proposed genetic algorithm (without local search phase) is run with four different values (0.2, 0.4, 0.6 and 0.8) for crossover probability. Figure 2 shows the effect of changing Рс on GA. In figure 7, the horizontal axis display the number of generations and vertical axis shows the fitness of the best solution. As seen in figure 6, the ability of GA for finding the optimal solution improves when the value of ?c increases from 0.2 to 0.8. This occurs because when we choose a large value for PQ, the possibility of generating new solutions increases and search is getting wider. Figure 7: Fitness of GA algorithm under different values of P £ Figure 8:Fitness of GA algorithm under different values of Pm C. Comparison of the fitness of FGARI with GA and RI algorithms As described in section IV, FGARI is a hybrid algorithm based on GA and RI algorithms. In this experiment has shown that the proposed algorithm FGARI has better performance than its constructive algorithms (GA and RI). Figure 8 demonstrates the average fitness of each algorithm in each generation. From the slope of the GA curve in figure 8 can be concluded that the GA after a while stuck in local optimum. However, RI algorithm has the ability to achieve the optimal solution, but its convergence speed is very low. By combining GA and RI in FGARI, the speed of GA and the ability of exploitation RI have been used simultaneous. The results are shown in Figure 9 confirms this. B. Evaluation the effect of mutation probability parameter on proposed GA Mutation probability ( Pm ) is another important parameter that influence the efficiency of GA. Figure 8 shows the behavior of GA with different values ofp. From Figure 7, it can be seen that when the value of ^mincreases from 0.1 to 0.5, the performance of GA improves due to the possibility of generating new solutions increases. However, when the value of Pm is further raised, the performance of GA drops. This occurs because a large value of Pm cause a suddenly change, and after a few generations, GA may be trapped in a suboptimal state, and Hence, cannot obtain the optimal solution. Figure 9: Fitness of FGARI, RI and GA algorithms in each generation D. Comparison of the fitness of FGASA with GA and SA algorithms Figure 10 displays the performance of FGASA algorithm, which is combination of GA and SA algorithms, in comparison with its fundamental algorithms regarding the fitness. Simulation results show that combining GA and SA algorithms in FGASA reach a better solution in less time. Also, SA algorithm has low convergence speed, but don’t trap in local optimum same as RI. F. Comparison of the fitness of three proposed algorithms (FGARI, FGASA and FGATS) Figure 12 shows the efficiency of three proposed algorithm. As mentioned in section VI, the base of the three algorithms is same and the only difference is in the local search method that is used in them. As seen in Figure 10, FGATS has the best performance and FGARI has the worst performance. However the performance difference is not very significant and all three algorithms have acceptable ability to solve the UCTP. -—GA — FGASA —FGASA —FGATS 1KB 1500 2003 Number of generations Figure 10:Fitness of FGASA, SA and GA algorithms in each generation E. Comparison of the fitness of FGATS with GA and TS algorithms FGATS has been combined from GA and TS algorithms. Figure 11 shows that FGATS algorithm has generally better performance for solving UCTP than its constructive algorithms (GA and TS). 500 1000 1500 2000 291 ЗОЮ Number of generations Figure 12 : Fitness of FGARI, FGASA and FGATS algorithms in each generation Number of generations Figure 11:Fitness of FGATS, TS and GA algorithms in each generation Figure 13: Fitness of FGARI, FGASA, FGATS, RI, SA, TS and GA algorithms on each datasets of table 1 Figure 13 demonstrates the result of comparison of three proposed algorithm with their fundamental algorithm on different datasets in table 1. The horizontal axis shows the dataset number and vertical axis is the fitness of best solution that obtained by each algorithm. For achieve the results shown in figure 13, we had executed all algorithms for a specific same period of time. From Figure 13, it is seen that all algorithms have almost the same results for small datasets. But, this similarity becomes less in larger datasets. Generally, with increasing the size of datasets, fitness decrease. However FGATS has the more acceptable fitness than other algorithm particularly when the dataset is large. H. Comparison of the execution time of three proposed algorithms (FGARI, FGASA and FGATS) on different datasets Table 3 shows required time for FGARI, FGASA and FGATS algorithms to satisfy 70% soft constraints (reach fitness 210) in terms of second on each dataset of table 1. As mentioned in section VI, the base of these algorithms is same and the only difference is in the local search method that is used in them. With regarding the pseudo-code of three local search algorithms, which have been shown in figure 3, figure 4 and figure 5, the time complexity of them is same. Therefore the GA algorithm with TS can find optimal solution in less time, especially when the dataset is large. Table 3: Required time (in terms of second) of FGARI, FGASA and FGATS algorithms to satisfy 70% soft constraints Dataset number FGATS FGASA FGARI 1 79 74 73 2 302 312 320 3 598 623 631 4 1476 1682 1785 5 2191 2312 2459 6 2904 3201 3400 7 4025 4216 4561 8 5143 5418 5721 9 6230 6761 7015 I. Evaluation the performance of multi population version of proposed genetic algorithm In tables 4, 5, 6 efficiency of two population version of proposed algorithm with the centralized version according to execution time has compared. The in this table show he required run time in terms of second to guarantee 70% soft constraints on different datasets. The general properties of datasets are presented in table 3. In this experiment to assessment the performance of multi population version, the main population is partitioned into two populations with 50 members and evolved separately. As seen in tables 4, 5, 6 the required execution time in multi population version is approximately less for all datasets. Table 4: Comparison of the required execution time of multi population version of proposed algorithm with centralized version on different datasets( FGARI) Dataset Centralized version of proposed algorithm Multi population version of proposed algorithm 1 73 71 2 320 253 3 631 471 4 1785 1270 5 2459 1845 6 3400 2213 7 4561 3011 8 5721 3402 9 7051 3893 Table 5: Comparison of the required execution time of multi population version of proposed algorithm with centralized version on different datasets( FGASA) Dataset Centralized version of proposed algorithm Multi population version of proposed algorithm 1 74 70 2 312 251 3 623 469 4 1682 1193 5 2312 1803 6 3201 2150 7 4216 2987 8 5418 3368 9 6761 3822 Table 6: Comparison of the required execution time of multi population version of proposed algorithm with centralized version on different datasets( FGATS) Dataset Centralized version of proposed algorithm Multi population version of proposed algorithm 1 79 71 2 302 233 3 598 415 4 1476 973 5 2191 1579 6 2904 1982 7 4025 2721 8 5143 3043 9 6230 3557 VI. Conclusions And Future Works In this study, we proposed three algorithms FGARI (Fuzzy Genetic Algorithm guided by Randomized Iterative local search algorithm), FGASA (Fuzzy Genetic Algorithm guided by Simulated Annealing algorithm) and FGATS (Fuzzy Genetic Algorithm guided by Tabu Search algorithm) for solving UCTP. These algorithms are based on heuristics RI (randomized iterative), SA (Simulated Annealing), TS (Tabu Search), GA (Genetic Algorithm) and fuzzy logic. Due to the random nature of genetic operators in GA, classical genetic algorithms extremely violate the hard constraints during the evolution process. This makes the algorithm convergence time is too long. To solve this problem, genetic operators have been genetically modified to not allow any hard constraints are violated, in other words, the proposed algorithms work on feasible solutions and try to satisfy the soft constraints as possible. Also, the classical genetic algorithm because of its high emphasis on exploration may be trapped in local optimum. Therefore in the proposed genetic algorithms after applying the genetic operators, local search methods (RI, SA and TS) has been used to ability of exploitation of the proposed GA algorithms can be strengthened. Because the algorithm work on feasible solutions, the fitness function is depended only on meeting soft constrains. But, the soft constraints have not binary property and they are somewhat qualitative, vague and uncertain. Also, they are sometimes in conflict with each other. To overcome this ambiguity and uncertainty, the fitness of a solution in proposed algorithms is determined using fuzzy logic by a set of fuzzy rules. In order to test the performance of proposed GAs for the UCTP, experiments were carried out to analyze the sensitivity of parameters and the effect of local search algorithms for the performance of GAs based on a set of benchmark UCTP instances. Simulation results have shown that performance of GA is very sensitive to crossover Probability and mutation probability. Large value for crossover Probability (near to 0.8) and average value for mutation probability (0.4 to 0.6) are able to produce good results. The experimental results show that the proposed FGATS is competitive and works reasonably well across all problem instances in comparison with other approaches. Generally, with the help of the local search, GA is able to efficiently find optimal or near-optimal solutions for the UCTP, and hence, can act as a powerful tool for the UCTP. However, the proposed algorithms with regarding to assumed constraints and performed simulations have been shown acceptable performance for solving university course timetabling but they should be evaluated for more real environments with more constraints in future. The idea of a hybrid solution for solving UCTP is very open. For example, instead the GA in proposed algorithms optimization ant colony algorithm or multi population GA can be used. Performance of RI, SA and TS is very sensitive to neighborhood structures. We can focus on design more efficient neighborhood structure. Also, given that the proposed algorithm have been introduced to UCTP, modified version of this algorithm can designed for solving university exam timetabling problem. Many uniprocessor approaches are purposed in literature solving UCTP, multiprocessor versions of these algorithms can be considered as future work.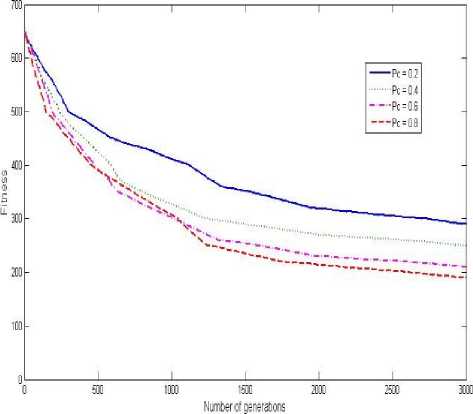
Список литературы Multi Population Hybrid Genetic Algorithms for University Course Timetabling Problem
- Abdullah S. “Heuristic Approaches for University Timetabling Problems”. PhD thesis, School of Computer Science and Information Technology, The University of Nottingham, United Kingdom, 2006.
- ShahvaliM., SanieeM., SajediH. “A fuzzy genetic algorithm with local search for university course timetabling”, pp.250-254, 2011.
- Yang S, Jat S. N. “Genetic algorithms with guided and local search strategies for university course timetabling”. IEEE Transactions on System, Man, and Cybernetics -PART C: Applications and Reviews, vol. 41, NO. 1, January, 2011.
- Abdullah S, Burke E. K, McCollum B. “Using a randomized iterative improvement algorithm with composite neighborhood structures”. Proceeding of 6th International Conference on Meta-heuristic, pp. 153–169, 2007.
- Chaudhuri A, De K. “Fuzzy Genetic Heuristic for University Course Timetable Problem”. International journal of Advance Soft Computing Application, Vol. 2, No. 1, March, .2010.
- Daskalaki S, BirbasT, Housos E. “An integer programming formulation for a case study in university timetabling”. European Journal of Operational Research, 153, 117–135, 2004.
- Khuri S, Walters T, Sugono Y. “A grouping genetic algorithm for coloring the edges of graphs”. Proceeding of the ACM/SIGAPP Symposium on Applied Computing, ACM Press, pp.422-427, 2000.
- White G, Xie B, Zonjic S. “Using tabu search with longer term memoryand relaxation to create examination timetables”. European Journal ofOperational Research, Vol.153, No.16, pp.80-91, 2004.
- Welsh D. J. A, Powell M. B. “The upper bound for the chromatic number of a graph and its application to timetabling problems”. The Computer Journal, vol. 11, pp. 41–47, 1967.
- Burke E. K, Kendall G, Soubeiga E. “A tabu-search hyper-heuristic for timetabling and rostering”. Journal of Heuristics. 9(6), pp 451-470, 2003.
- Smith KA, Abramson D, Duke D. “Hopfield neural networks for timetabling: formulations methods, and comparative results”. Computers andIndustrial Engineering,44(2):283–305, 2003.
- Cambazard H, Demazeau F, Jussien N, David P. “Interactively solving school timetabling problems using extensions of constraint programming”.Lecture notes in computer science, vol. 3616, Berlin: Springer;p. 190–207, 2005.
- Wren A. “Scheduling, Timetabling and rostering—a special relationship,the practice and theory of automated timetabling”. Lecture notes incomputer science, vol. 1153, Berlin: Springer, p. 46–76, 1996.
- Asmuni H, Burke E. K, Garibaldi J. M. “Fuzzy multiple heuristicordering for course timetabling”. Proceeding of the 5th United Kingdom Workshop on Computational Intelligence,London,pp. 302–309, 2005.
- Burke E. K., MacCloumn B., Meisels A., Petrovic S., and Qu R.“A Graph-based hyper heuristic for timetabling problems”.European J of Oper Research, 176: 177–192, 2006.
- Rossi-Doria O, Sampels M, Birattari M, Chiarandini M, DorigoM,Gambardella L, Knowles J,Manfrin M, Mastrolilli M, PaechterB,PaqueteL,St¨utzle T. “A comparison of the performance of differentmeta-heuristics on the timetabling problem”. Proceeding of 4th International Conference Practical Theory Automated Timetabling (Lecture Notes in Computer Science), vol. 2740, pp. 329–351.
- Socha K, Knowles J, Samples M. “A max-min ant system for the university course timetabling problem:. Proceeding of the 3rd International Workshop on Ant Algorithms, Lecture Notes in Computer Science, Springer Verlag, Vol.2463, pp.1-13, . 2002.
- Zervoudakis K, Stamatopoulos P. “A generic object-oriented constraint-based model for university course timetabling” .Proceeding of 3rdInternational Conference on the Practice and Theory of Automated Timetabling, Germany, Springer-Verlag. pp 28-47, 2001.
- Abdullah S., Burke E. K., and McCollum B.“A Hybrid EvolutionaryApproach to the University Course TimetablingProblem”. Proc of the 2007 IEEE Congres on EvolComput.,pp. 1764–1768, 2007.
- Alkan A., OzcanE..“Memetic algorithms for timetablingevolutionary computation”. Proc of the 2003 IEEE CongressonEvolComput., vol. 3, pp. 1796–1802, 2003.
- BroderS.“Final examination scheduling”. Comm of the ACM,7(8): 494–498, 1964.
- Ten Eikelder HMM, Willemen RJ. “Some complexity aspects of secondary school timetabling problems”. Lecture notes in computer science,vol. 2079, Berlin: Springer; p. 18–27, 2001.
- Papoutsis K, Valouxis C, Housos E. “A column generation approach for the timetabling problem of greek high schools”. Journal of the OperationalResearch Society, 54(3):230–8, 2003.
- Valouxis C, Housos E. “Constraint programming approach for school timetabling”. Computers and Operations Research, 30(10):1555–72, 2003.
- Caldeira JP, Rosa A. “School timetabling using genetic search”. In proceedings of the second international conference on the practice and theoryof automated timetabling (PATAT’97), p. 115–22, 1997.
- Fernandes C, Caldeira JP, Melicio F, Rosa AC. “Evolutionary algorithm for school timetabling”. InProceedings of the genetic and evolutionarycomputation conference (GECCO’ 99), vol. 2, p. 1777–83, 1999.
- Bufé M, et al. “Automated solution of a highly constrained school timetablingproblem-preliminary results”. Lecture notes in computer science, vol. 2037, Berlin: Springer; 2001. p. 431–40.
- Burke E. K.,LandaSilvaD. J.“The design of memetic
- algorithms for scheduling and timetabling problemsInN. Krasnogor, W. Hart, and J. Smith (eds.)”, Recent AdvancesinMemetic Algorithms, Studies in Fuzziness and Soft Computing,vol. 166, pp. 289–312, 2004.
- http://www.cs.qub.ac.uk/itc2007.


