Multiclass Arrhythmia Classification from Imbalanced ECG Data Using Encoded Transformer based CNN-LSTM Hybrid Model

Cardiac arrhythmia also commonly known as irregular heartbeats is a global health concern that affects people of all ages and socio-economic background. In 2021, 20.5 million peoples are died from heart diseases that is approximately 33% of total deaths of that year as reported [1]. Cardiovascular abnormalities or arrhythmia which led patients to serious heart attack and stroke are also responsible for these deaths. These diseases has huge impact on where healthcare systems and resources are limited and it is reported that about 80% of the total cardiovascular diseases related deaths are occurred in countries with low or medium economy [2]. Arrhythmia detection and classification has a great impact on medical progress, public health care systems and accurate treatments. Conventional methods for arrhythmia detection and classification could be time consuming and subjective because they need manual interpretation by expert medical professionals. In this revolutionary era of artificial intelligence, machine learning especially deep learning based automatic classification is a remarkable solution for such problem [3]. Recently, deep learning is an advanced sub-area of artificial intelligence that works as a robust tool for categorizing ECG signals extracting the complex features in an automatic way [4]. Convolutional neural network is a deep learning concept that has impressive results for the detection of arrhythmia more effectively that helps proper diagnosis of the patients. It can process the raw ECG data [4] and automatically extract the features more precisely without the necessity of manual interpretation.

Different researches heave been reported in the literature to classify arrhythmias using both conventional machine learning and deep learning techniques [5-19]. In conventional machine learning domain, the performance for multiclass classifier is not so satisfactory especially for larger test data. On the contrary, many recently methods utilize deep learning methods with remarkable performance for the categorization of multiclass ECG arrhythmias [8-16]. CNNs captures information of ECG signals as well as identify fluctuations in QRS complexes which are treated as small abnormalities [8]. Recently, LSTMs show their powerfulness in handling sequential data like ECG highlighting the ability to intent the vanishing gradient problem [18,19]. But these networks have some challenges in their individual form e.g. they can perform well in common types of arrhythmias but poor in rare types of classes. On the other hand, both in-beat information and beat-to-beat temporal dependencies cannot be captured without hybrid models. These challenges may lead to reduce the effectiveness and performances of convolutional and recurrent neural networks. Therefore, an effective fusion of them might combine advantages of them to boost the overall classification performance suppressing individual limitations. Furthermore, the long range dependencies in the ECG waveform can be captured by the encoded transformer module to extract efficient features. Therefore, a fusion of CNN-ET-LSTM mechanism could be a notable solution for enhancing the performance in multiclass arrhythmia classification task. Another issues to be considered that the dataset of arrhythmias is practically imbalanced, which affected the learning of the classifier. Hence, consideration of the balancing the class-wise is important. Sampling methods could be used to balance the imbalance data. Hybrid model of CNN and LSTM can capture both temporal dependencies and feature extraction. Attention mechanism could be used for improving feature extraction. Being motivated from the above issues and solution strategies, this research aims to propose a robust and accurate system for the categorization of five distinct types of arrhythmias by employing a hybrid model referred to as CNN-ET-LSTM. In this model, CNN is mainly used as a feature extractor. Batch normalization is used after each convolutional layer to stabilize the training process as well as improve efficiency. Long range dependencies and relationships in the ECG waveform are captured by the encoded transformer module. Considering the beat-wise temporal context of the signal, the LSTM processes feature sequentially. The SMOTE technique synthetically generates additional data of minority classes in order to balance the whole dataset which helps to put down the majority and minority class imbalance problem. This guarantees that the model undergoes training on an inclusive and representative dataset, preventing biases towards the majority class. Hence, the combined CNN and LSTM model with encoded transformer enhanced with the SMOTE technique for addressing class imbalance represents a robust solution for ECG arrhythmia classification. By effectively leveraging both in-beat information and beat-to-beat temporal dependencies while ensuring a balanced representation of different arrhythmia classes, this approach holds the promise of substantially enhancing the precision of arrhythmia diagnosis, ultimately resulting in improved cardiac care. The research contributions are outlined as follows:

• •    Developing a novel encoded transformer based CNN-ET-LSTM model that leverages the strengths of both CNNs and LSTMs with transformer module for ECG arrhythmia classification.

• •    A strategy for handling imbalanced datasets using SMOTE technique that presents a comprehensive solution to handle the challenges presented by class imbalance.

• •    Experimental evaluation of the suggested model on a MIT-BIH arrhythmia database is found significant with accuracy of 97.52% for five-class classification scenario comparing with existing related works for ECG arrhythmia classification.

2.    Related Works 3.    Proposed Methodology

This paper is organized as: Section 2 provides an overview of researches related to this work. Section 3 covers the proposed methodology describing the system architecture, data collection and processing, as well as performance evaluation parameters of the proposed system. Experimental results and their analysis are outlined in Section 4 along with a discussion on the findings. Section 5 presents a conclusion of the paper.

Researchers have proposed different methods to classify the types of arrhythmias. In conventional machine learning domain, the performance for multiclass problem is not so satisfactory. Vandana Singh et al. [5] employed support vector machines (SVM) classifiers to categorize four arrhythmia classes, utilizing principal component analysis (PCA) to minimize the dataset's attribute count. This classifier achieves an accuracy of 92.96%. Shivajirao M. Jadhav et al. [6] proposed some multilayer perceptron (MLP) neural network model, generalized feedforward neural networks and modular neural network (MNN) to diagnose the diseases caused by cardiac arrhythmia. Among these three networks, MLP achieves the highest accuracy of 86.67%. Many recently reported methods utilize deep learning methods satisfactorily for the categorization of multiclass ECG arrhythmias which we will discuss in this review considering the relevance with our proposal in this paper. Ali Mohammad Alqudah et al. [7] achieved an accuracy of 93.8% using CNN considering six classes of arrhythmia. U. Rajendra Acharya et al. [8] created a CNN of 9-layers to classify five arrhythmia classes, achieving an accuracy of 94.03% on the arrhythmia dataset. Hassan et al. [9] compare the performance between deep CNN and LSTM algorithm considering five classes of arrhythmia. In terms of performance metrics, CNN performs better than LSTM. Parul Madan et al. [10] created a hybrid deep learning algorithm combining 2D-CNN and LSTM for arrhythmias classification. In this technique, 2D scalogram images are produced from 1D-ECG signals from arrhythmia database for extracting feature. The overall accuracy is evaluated considering three classes of arrhythmia. Xue Xu et al. [11] established an innovative method which is the combination CNN and bidirectional LSTM to interpret the ECG rhythm. The accuracy, average sensitivity and specificity considering five classes of arrhythmia using this method are 95.90%, 95.90% and 96.34% respectively. Bahareh Pourbabaee et al. [12] focused on patients with paroxysmal atrial fibrillation (PAF). A CNN system is employed to derive and categorize data attributes with precision of 93.60%. Shalin et al. [13] used MLP and CNN to identify eight types of arrhythmias. The MLP attains an accuracy of 88.7%, while the CNN achieves a accuracy of 83.5%. Y. Xia et al. [14] proposed deep CNN to observe atrial fibrillation. It analyzes ECG segments by short term Fourier transform (STFT) and stationary wavelet transform (SWT). Wenhan Liu et al. [15] proposed multilead-CNN for detecting myocardial infarction. The system has achieved accuracy, sensitivity and specificity of 96.00%, 95.40% and 97.37% respectively. Dong et al. [16] proposed a vision transformer based categorization of arrhythmia for 12 lead ECG with 9 classes of heartbeat. The system achieves F1-score of 82.9%. Recurrent Neural Networks (RNNs) are also found suitable for the detection of heart abnormalities as they excel the sequential nature of the ECG waveform [17]. LSTMs are the modifications of RNNs that have the ability to intent the vanishing gradient problem and hence showing more potentiality in arrhythmia classification [18,19]. Few other works are mentioned in the Table 5 for performance comparison with proposed work. In our previous study [20], we have observed that effective combination of CNN and LSTM can enhance the overall performance. Furthermore, recent researches showing the promises of encoded transformer in feature extraction and selection [21] in various applications.

The motivation behind employing a CNN-ET-LSTM network in this study for categorization of ECG arrhythmias is to leverage the strengths of both CNNs and LSTMs with transformer module extracting the multifaceted nature of electrocardiogram signals. ECG signals exhibit intricate temporal patterns, necessitating a network capable of capturing long-range dependencies which is strength of LSTM networks. For identifying beat patterns within the waveform, CNNs are used because they are good at it. An important challenge when working with deep architectures is the stability of the network. Batch normalization handled this challenge and kept the network stable. The transformer module has an attention mechanism and is suitable for capturing long range relationships of the signal. The integration of these networks with an encoded transformer learns from the different representations of the ECG arrhythmias. This ensures the model has the ability to cope up with the short time and longtime patterns in the dataset as well as wide variations of irregular heartbeats. It also minimizes frequent problems in deep learning applications to ensure a more comprehensive and reliable model for classifying arrhythmia more precisely. Overall, the proposed model could be an effective tool for classifying heart abnormalities and be a better solution to this five-class classification problem.

The proposed CNN-ET-LSTM model is the combination of two powerful neural networks CNN and LSTM with a transformer module, which leverages the strength of each network. Each portion has different advantages to deal with the ECG arrhythmia data. After the step of data collection and preprocessing, the proposed model receives data as input and further converted to suitable format which is coherent with neural networks. The CNN portion identifies complex patterns and spatial characteristics of the ECG data. Sequential patterns and temporal dependencies with the data are identified by the LSTM component of the network. The harmonious combination of these components has the ability to find temporal evolution and localized problems. Through rigorous training on labeled ECG datasets, the system attains a high degree of precision in the classification of the five arrhythmias.

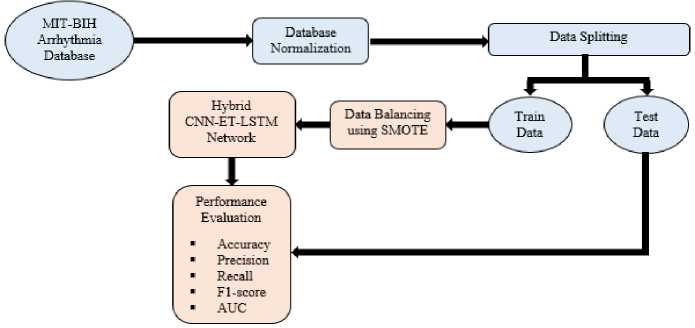
Fig.1. Proposed Methodology for the ECG based arrhythmia classification using hybrid CNN-ET-LSTM network

Fig. 1 illustrates the overview of the proposed methodology for ECG based arrhythmia classification. Firstly, the dataset is normalized first. Then the data is divided into training data and testing data. SMOTE is applied to train data for balancing. This makes the system to perform more efficiently on classes with minimum number of samples. The train data is used to train the proposed CNN-ET-LSTM model. Finally, the model's effectiveness is assessed with different types of performance parameters.

• 3.1.    Data Collection and Preprocessing

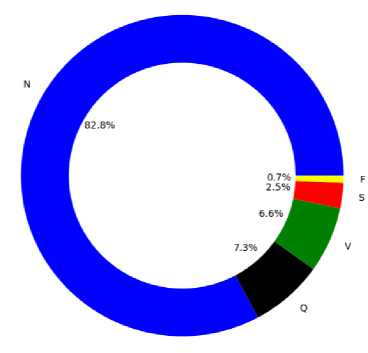
  The dataset employed in this research is a widely accepted MIT-BIH arrhythmia database [22,23] because it has rich diversity of data, high quality annotation, long duration recordings and real world data. It serves as a standardized reference dataset for assessing and contrasting the effectiveness of algorithms in the field of arrhythmia detection and classification. The data in this database was collected from real patients; it becomes a benchmark resource for examining arrhythmias within a clinical context. This means that the data reflects the variability and complexity often encountered in real-world scenarios. In Beth Israel Hospital (BIH) arrhythmia Laboratory between the year of 1975 and 1979, the database comprises 48 thirty-minute segments of two-channel ECG recordings of 47 patients [23]. 23 recordings were obtained from a diverse population, consisting of approximately 60% inpatients and 40% outpatients at Beth Israel Hospital in Boston was a part of the 4000 24-hour ambulatory ECG recordings. The remaining 25 recordings to encompass less common yet clinically significant arrhythmias were specifically selected from the same dataset that wouldn't be properly represented in a small random sample. The sampling rate of the signal is 360 Hz and amplitude rage is 10 mV. There are 109446 of cases in the whole dataset and it features five classes of arrhythmia. The percentage of each class of arrhythmia and their class label is given in Table 1.

Table 1. Percentage of each classes of arrhythmia and their class label

Arrhythmia Classes	Class Label	Percentage of Each Class
N	0	82.8%
S	1	2.5%
V	2	6.6%
F	3	0.7%
Q	4	7.3%

The data is normalized between 0 and 1 for enhancing the performance of the model, lowing instability issue as well as makes faster convergence. The non-ectopic beats (N) have the highest percentage (82.8%) where the fusion beats (F) have the lowest percentage (0.7%) in the dataset, which means it is an imbalanced dataset. But, working with imbalanced datasets is a challenge because most machine learning algorithms overlook the minority class, which results in poor performance [24]. Addressing this problem involves oversampling instances from the minority class, and a straightforward approach to adapting a model includes duplicating samples from the smaller class in the training dataset. While this technique helps equalize the class size, it does not enter any new data to the model. This goal can be achieved using a widely used data balancing techniques named synthetic minority oversampling technique (SMOTE) [25].

Applying SMOTE

(a)

(b)

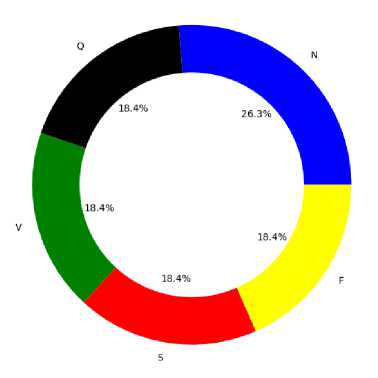
Fig.2. Percentage of records of each arrhythmia types in the database after balancing with SMOTE (a) Imbalanced data (b) Balanced data

Fig. 2 shows the effect of applying SMOTE on an imbalanced data and how the dataset looks like after data balancing. In this work, SMOTE is applied to train data only because it holds the integrity of the test data and shows real performance of the model. To balance the classes appeared in the dataset, firstly minority classes are oversampled and then reduce the majority class by under sampling. The minority classes are oversampled using SMOTE with sampling strategy of 0.5. Then the majority class is under sampled using Random-Under-Sampler with sampling strategy of 0.7. From the above figure, it is seen that there are no majority and minority classes in the balanced database. This database is suitable for training and also helpful to improve the performance especially on minority classes. The dataset was splitted into 80% of train data and 20% of test data. Five-fold cross validation technique is used for validation.

• 3.2.    Description of the Proposed CNN-ET-LSTM Model

The proposed network is the integration of CNN, encoded transformer (ET) and LSTM for the categorization of five distinct types of ECG arrhythmia using a benchmark arrhythmia database. Brief descriptions of these methods are given below.

• A.    Convolutional Neural Network (CNN)

The customized 1D CNN is architecture designed for handling one-dimensional sequences of ECG beat frame data. Unlike traditional artificial neural networks, CNNs leverage convolutional layers to automatically extract the input sequence’s relevant features [26]. This is accomplished through the application of small filters that slide over the data, capturing local patterns and encoding them into higher-level representations. The activation of these filters is governed by the learned weights, allowing the network to adapt and recognize intricate patterns within the data. As the network progresses through numerous convolutional layers, it acquires the capacity to discern increasingly complex features. The subsequent pooling layers function to down-sample the data, focusing on the most salient information while reducing computational complexity. This stepwise feature extraction process, combined with the introduction of non-linearity through activation functions, equips CNNs with the ability to effectively categorize ECG sequential data. A general architecture of CNN is shown in Fig. 3 and the layers of the CNN model are briefly described below:

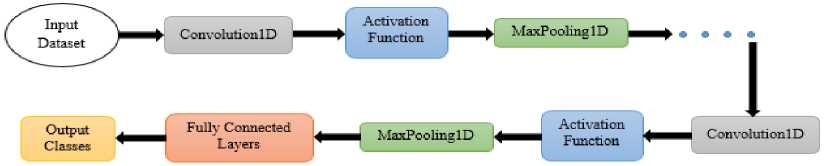
Fig.3. A General architecture of CNN.

Convolutional layer with batch normalization : The fundamental component of a 1D-CNN is the convolutional layer. Within a 1D convolutional layer, a group of filters is employed over the input ECG sequence to identify localized patterns. The output of these filters creates a feature map. Each filter learns to recognize different patterns or features. The mathematical equation of the convolution can be expressed as:

(f * g)t) = / f(^g(t - т)с/т

Where, f refers to the input sequence, g represents the filter kernel and t denotes the position in the output sequence.

Batch normalization is a method employed in deep learning to enhance the training efficiency of neural networks [42]. For a given channel's activations in a mini-batch, the normalization can be expressed as:

X =

X-^

0 2 -€

Where, x denotes input to the batch normalization layer, μ denotes mean of the batch, σ ² denotes variance of the batch and ϵ is a constant to avoid the problem caused by division by zero.

Activation Function : After the convolution operation, an activation function such as rectified-linear unit is utilized element-wise to present non-linearity. This helps the system learn more complex patterns.

Pooling Layer : It minimizes the spatial dimension of feature maps while preserving essential information. We have used a frequently used pooling technique named Max pooling, which involves selecting the maximum value within a defined window.

Fully Connected Layers : Following a series of convolutional and pooling layers, it is common to introduce one or more layers that are fully connected. These layers leverage the high-level features acquired through the convolutional layers to generate a conclusive prediction.

Output Layer : Final layer of the network, depending on the task, might use different activation functions (e.g., softmax for multi-class classification).

• B.    Encoded Transformer (ET) Module

The encoded transformer module is a pivotal advancement in deep learning [27]. The long range dependencies in the ECG waveform can be captured by the encoded transformer module. The transformer module identifies the important parts of ECG that leads better sensitivity for arrhythmia detection. Furthermore, self-attentive mechanism has against adversarial input perturbations [28]. The automatic CNN classifier usually shows higher accuracy for denoised ECG [8]. However, denoising of ECG requires additional signal processing tasks [29,30], where performance might vary among applied techniques. In this study, we have not applied ECG processing considering this issue. Rather, we have utilized the noise robustness benefits of the attention mechanism based encoded transformer adding a module to the CNN-LSTM model. The conceptual structure of transformer encoder is depicted in Fig. 4. The mathematical formulation of the key components of the module are mentioned below:

Multi-head self-attention:

• •    Let X be the input and W ® , W^K , W^v be learned weight matrices.

• •    Compute Query ( Q ), Key ( K) , and Value ( V ) matrices: Q = X-W ® ,K = X'W^K , V = X-W^v

QKT

• •    Compute scaled dot-product attention scores: Attention = softmax (   ) V

• •    d_k represents the dimension of the Key vectors.

Addition of residual connection and layer normalization:

Layer- . =LayerNorm( X +Attention)

Position-wise feedforward neural network:

• •    Let W 1 , b 1 and W 2 , b₂be the learned weight matrices and biases.

• •    Compute feedforward neural network output: FFN =ReLU( X-W 1 + b 1 )-W 2 + b 2

Another residual connection and layer normalization:

Layer 2 =LayerNorm(Layer 1 + FFN)

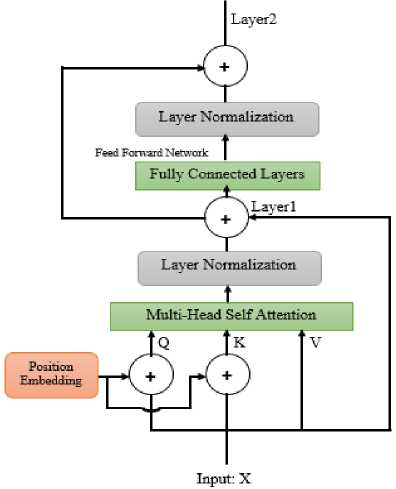
Fig.4. Encoded transformer module

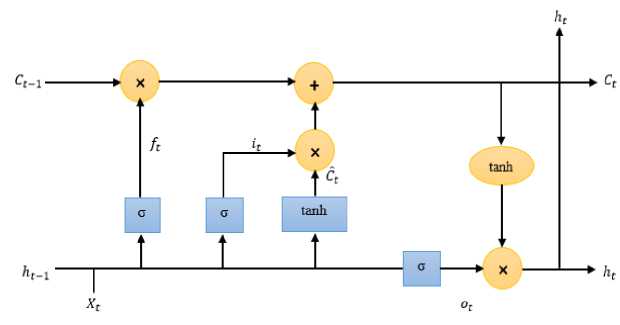
Fig.5. A general architecture of lstm cell

• C.    Long Short-Term Memory (LSTM) Layers

LSTM networks represent a specialized type of RNN designed to effectively model sequential data [31]. In the environment of temporal data, such as financial market trends or physiological signals, LSTMs can discern patterns and anomalies that might span over a considerable duration. By training on labeled data, LSTM networks learn to map input sequences to their respective classes, making them exceptionally adept at tasks like sentiment analysis, speech recognition, and various forms of time series classification. Their adaptability and capacity for handling complex temporal relationships have solidified LSTMs performance in the field of machine learning, particularly for tasks involving sequential data. A general structure of LSTM cells is portrayed in Fig. 5.

LSTM architecture: A standard LSTM network comprises of multiple LSTM cells arranged in a sequence. The output at time t of one LSTM cell is fed as input at time t +1 to the next LSTM cell. The overall output can be taken from the last LSTM cell to the final hidden state. An example of a simple architecture for a single-layer LSTM architecture is given by:

• •    Input Sequence (X 1 ,X 2,.......... ,X_t )

• •    LSTM Layer (with multiple LSTM cells, each processing X_t )

• •    Output (can be taken from the last time step or from a fully connected layer)

For more complex tasks or deeper architectures, multiple LSTM layers on top of each other or combined with other types of layers (e.g., dense layers or other types of recurrent layers).

Gates interpretation:

• •    Input Gate (i_t ): Measures the extent to which new data C_t will be included to state of the cell.

• •    Forget Gate (f_t ): Governs how much of the prior cell state (C_t-1) will be retained.

• •    Output Gate (o_t ): Decides how many of the cell state will be exposed as the hidden state.

• •    Cell Gate (C_t ): Determines the new data that will be included to the state of the cell.

LSTM cell: The core unit of an LSTM is called an LSTM cell. An LSTM cell maintains a hidden state h_t and a cell state C_t , which get updated at every time step t based on the input X_t and the prior states h_t-1 and C_t-1. The computations within an LSTM cell are defined by the following equations:

Input Gate, it = a(WuXt+bu+Whiht-i+bhi)(3)

Forget Gate, ft = a(WifXt+bif+Whfht-i+bhf)(4)

Cell Gate, C =tanh(WicXt + bic+Whcht-i+bhc)(5)

New Cell State, Ct =ft О Ct-1+itOC(6)

Output Gate, Ot = a(WloXt+bio +Whoht—1+bho)(7)

New Hidden State, ht=otOtanh(Ct)(8)

Here, a represents the sigmoid activation function, О signifies element-wise multiplication, and W along with b are matrices of weights and vectors of biases utilized for different gates.

• D.    Design of the CNN-ET-LSTM Network

The proposed model leverages both the strengths of CNN and LSTM with an encoded transformer to identify temporal dependencies and local patterns in the ECG data efficiently. Every portion of the model has different strength to analyze the ECG signal. CNN part is good at identifying local patterns of the ECG signal. The transformer encoder finds long range dependencies and the LSTM recognizes temporal dependencies of the data. This makes the model to classify arrhythmia with a wide range of variation of ECG data. The combination of these components could be a powerful tool to categorize distinct irregular heartbeats automatically and fasten the processing time for this task that revolutionized the cardiac healthcare systems, patients with arrhythmia and their diagnosis.

• Fig. 6 shows the illustration of the introduced CNN-ET-LSTM network using the given arrhythmia dataset for ECG arrhythmia categorization. The combined network has four CNN layers, one transformer module, two LSTM layers, four dense layers and one softmax function output layer. Each CNN layer block contains one convolution, batch normalization, ReLU function and one pooling layer. The first convolution layer uses filters of 64, kernels of 6, size of pool of 3 and strides of 2. The second convolution layer uses filters of 128, kernels of 3, size of pool of 2 and strides of 2. The third convolution layer uses filters of 128, kernels of 2, size of pool of 2 and strides of 2. The fourth convolution layer uses filters of 64, kernels of 2, size of pool of 2 and strides of 2. The intermediate output shape is (11, 64) after the convolution

• 3.3.    Performance Evaluation Matrices

block. The model uses embedded layer which has 64 dimensions, 2 attention heads that indicates multi-head attention mechanism and feed forward network with 4 hidden layers. The output shape of the transformer module is (11, 64). The first LSTM layer has 128 of units with rate of dropout of 20%. The second LSTM layer has 64 of units with rate of dropout of 20%. The number of units in four dense layers are 200, 100, 50 and 5 respectively. Five classes of data are grouped in the output layer. The total parameters of the proposed model are 296,713. The model is expected to be robust with data diversity than a simpler architecture without ET module that might struggle to generalize. The hyperparameters are tuned on trial and error basis to achieve an optimum performance. The summary in terms of layer type, output shape and parameters of introduced network is demonstrated in Table 2.

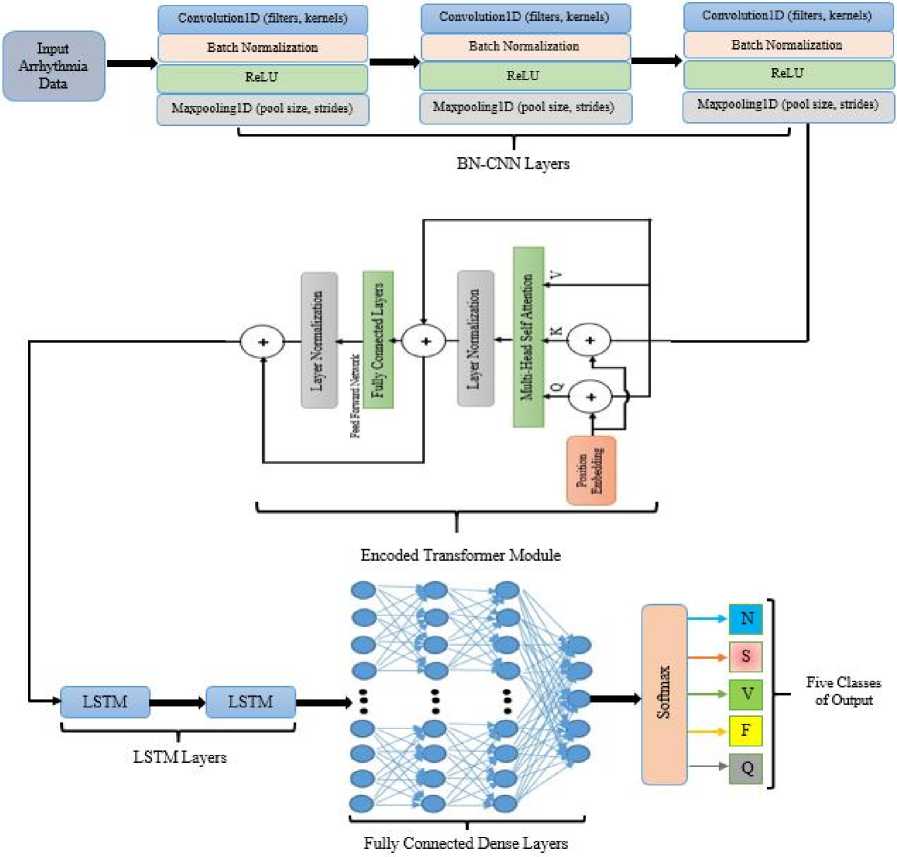
Fig.6. Architecture of the proposed CNN-ET-LSTM network for 5-Class ecg arrhythmia classification

The overall performance of the proposed hybrid CNN-ET-LSTM network for the classification of ECG arrhythmias is assessed in terms of accuracy, precision, recall, AUC and F1-score to assess the effectiveness of the model. These metrics provide insights into how well the model is performing in terms of classifying instances into the output classes and hence universally used to evaluate performance of such classifiers [32].

Accuracy: Accuracy is the ratio of accurately predicted instances among the total cases in the dataset.

Accuracy =

TP+TN

TP+TN+FP+FN

Precision: Precision is the proportion of true positives to the total of true positives and false positives. It emphasizes minimizing false positives.

Precision =

TP

TP+FP

Table 2. Layer-wise information of the proposed CNN-ET-LSTM architecture

Layer	Output Shape	Parameters
Input Layer	(1, 188)
Convolution1D	(182, 64)	448
BatchNormalization	(182, 64)	256
MaxPooling1D	(91, 64)	0
Convolution1D	(89, 128)	24704
BatchNormalization	(89, 128)	512
MaxPooling1D	(45, 128)	0
Convolution1D	(44, 128)	32896
BatchNormalization	(44, 128)	512
MaxPooling1D	(22, 128)	0
Convolution1D	(21, 64)	16448
BatchNormalization	(21, 64)	256
MaxPooling1D	(11, 64)	0
Transformer Module	(11, 64)	34052
LSTM	(11, 128)	98816
LSTM	64	49408
Dense	200	13000
Dense	100	20100
Dense	50	5050
Dense	5	255
Total Parameters: 296713
Trainable Parameters: 295945
Non-trainable Parameters: 768

Recall: Recall is the proportion of instances of true positives to the total instances of true positives and false negatives. It emphasizes minimizing false negatives.

TP

Recall = -!—                                     (11)

TP+FN                                                 v '

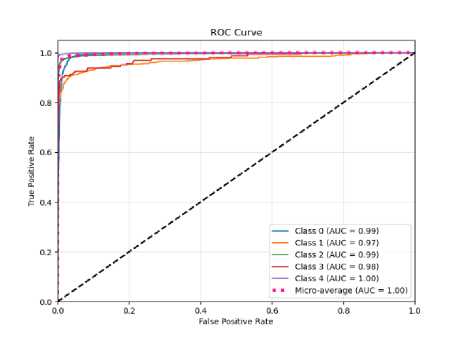
AUC: The area under the ROC curve (AUC) is a measure of a model's ability to distinguish between classes, where ROC (Receiver Operating Characteristic) curve is a plot of the true positive rate (TPR) versus false positive rate (FPR) at different thresholds. It illustrates the trade-off between sensitivity and specificity. The formulas for TPR and FPR are:

TPR =

TP

TP+FN

FPR =

FP

FP+TN

F1-score: F1-score is sub-contrary of precision and recall. It balances the parameters precision and recall.

F1-score

2xPrecistonxRecall (Precision+Recall)

Where, TP = Truly Positive, TN = Truly Negative, FP = Falsely Positive, FN = Falsely Negative instances, respectively.

4.    Experimental Result Analysis and Discussions

In this study, the MIT-BIH arrhythmia dataset was used to evaluate the effectiveness of the designed CNN-ET-LSTM network. Firstly, the dataset was split into 80% of train data and 20% of test data. SMOTE is used to maintain the imbalance problem of train data. The 5-fold cross-validation technique is considered using the training data. The experiment was done with epoch numbers of 60, 80, 100 and 120 to observe the consistency of performance of the network under different number of epochs. The model performance was evaluated with different matrices and further compared to other existing models. The model is implemented with TensorFlow in Keras and Python package on Intel 2.2 GHz Core i7 processor and performed using GPU NVIDIA GTX 1050 GeForce with RAM of 16 GB.

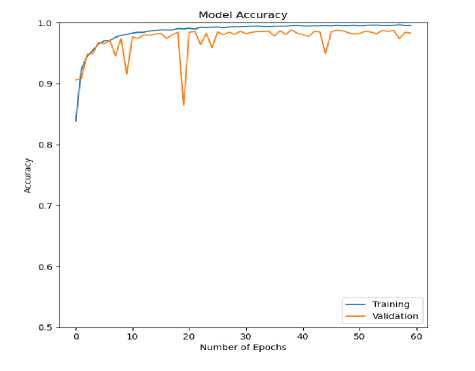
We have conducted an ablation study before reaching the final CNN-ET-LSTM model. Firstly, we have combined the CNN and LSTM network. Then we have added the batch normalization (BN) layers [33] to the CNN-LSTM previous network in order to see the impact of batch normalization. The BN-CNN-LSTM model accelerates the training process and also improves stability. There occurs a slight improvement in performance matrices when batch normalization layer is added to CNN with LSTM. Finally, we included the encoded transformer module to the BN-CNN-LSTM network. The model becomes more effective in terms of performance parameters if attention mechanism is introduced. Encoded transformer is suitable for handling imbalanced data and flexible with different input data types. To get the optimum results with the proposed CNN-ET-LSTM model, the hyperparameters are tuned before final selection. We have used ‘Adam’ optimizer tuning learning rate of 0.0001 to 0.01 and finally select 0.001 to get the best results. Batch size of 32 is used with the trial of 16, 64 and 128. The dropout rate also tuned from 0.2 to 0.5 and elect the value at 0.4. The filter size and kernel size of the convolutional layers also tuned with different size before final seection. The model is tested under different number of epochs to find the optimal epochs thus ensuring model reliability. Early stopping concept has been used to avoid the overfitting problem. This led the proposed CNN-ET-LSTM method has best results among all. A summarized result when the number of epochs are 60 is shown in Table 4. In summary, the hybrid model CNN-ET-LSTM includes three different components to form an effective solution for arrhythmia classification. Each component has distinct role for the classification of arrhythmia. The CNN component extracting the spatial features from signal. LSTM capturing the temporal dependencies and encoded transformer added the attention mechanism for bettering the representation. The final model is obtained adding components that improves the performance in different steps. A summarized result when the number of epochs is 60 is shown in Table 3.

Table 3. Performance comparison during the ablation study to reach the best model

Case (Model)	Accuracy (%)	Precision (%)	Recall (%)	F1-score (%)
CNN-LSTM	96.12	96.50	96.11	96.25
BN-CNN-LSTM	96.58	96.93	96.57	97.73
CNN-ET-LSTM	97.52	97.80	97.52	97.62

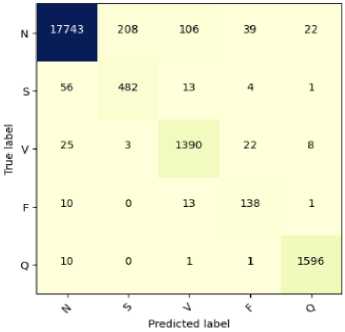
Confusion matrix

Classification accuracy is: 97.52%

(a)

Confusion matrix Classification accuracy is: 97.21%

(b)

Confusion matrix Classification accuracy is: 97.18%

(c)

Confusion matnx Classification accuracy is: 96.72%

(d)

(a)

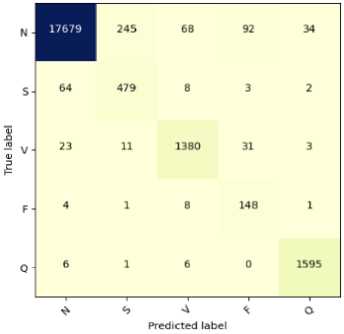
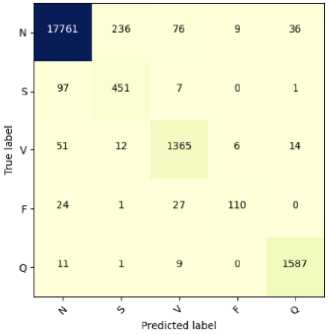
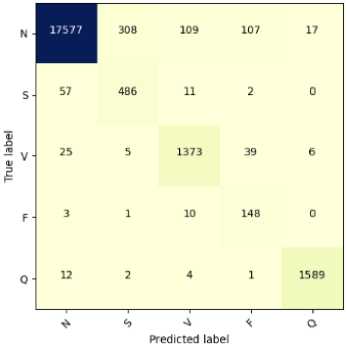
Fig.7. Confusion matrix for the classification of ECG arrhythmias based on proposed CNN-ET-LSTM network with different number of epochs (a) 60 (b) 80 (c) 100 and (d) 120

(b)

(c)

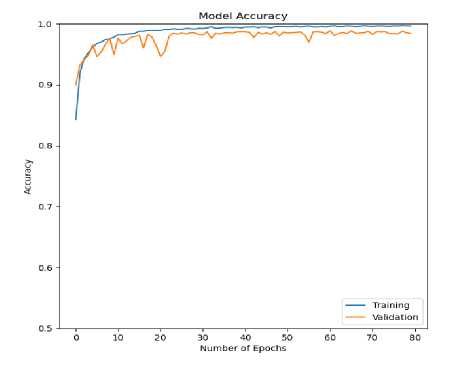
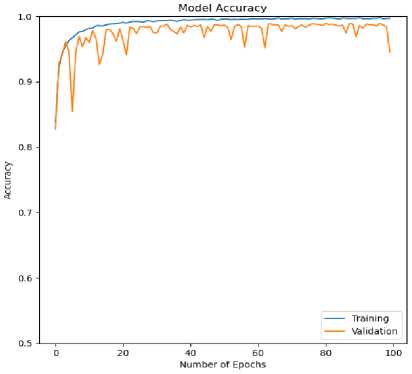
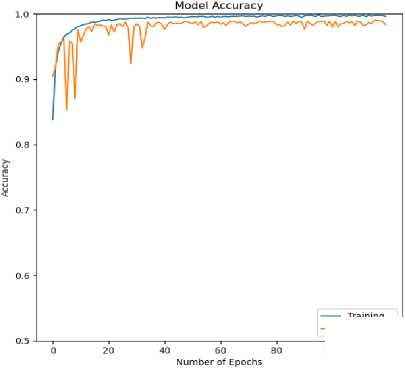
Fig.8. Accuracy (training and validation) curve for ECG arrhythmia classification based on the proposed CNN-ET-LSTM network with different number of epochs (a) 60 (b) 80 (c) 100 and (d) 120

---- Training

---- Validation

(d)

(a)

(b)

(c)

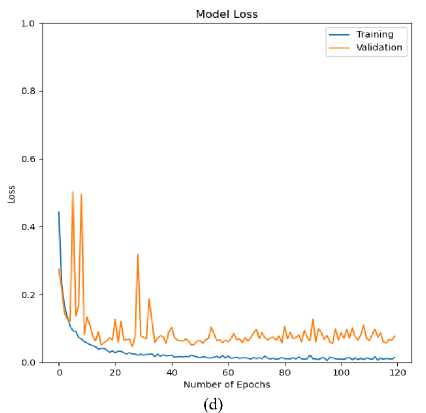
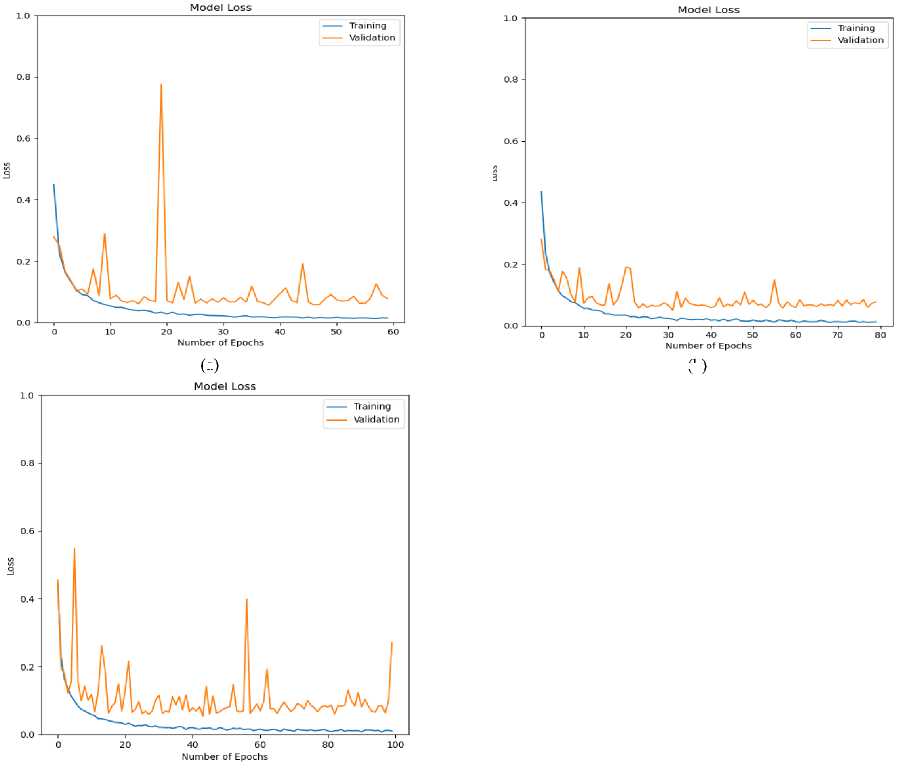
Fig.9. Loss (training and validation) curve for ECG arrhythmia classification based on the proposed CNN-ET-LSTM network with different number of epochs (a) 60 (b) 80 (c) 100 and (d) 120

The overall effectiveness of the suggested system is summarized and numerically shown in Table 4. The system has accuracy of 97.52%, precision of 97.80%, recall of 97.52%, and F1-score of 97.62% when the epoch numbers of 60. At epoch numbers of 80, these values are 97.21%, 97.73%, 97.20%, and 97.39% respectively. At epoch numbers of 100, the values of performance matrices are 97.18%, 98.40%, 97.17%, and 97.25% respectively. Epoch numbers of 120 has the accuracy of 96.72%, precision of 97.48%, recall of 96.71%, and F1-score of 96.97%.

Table 4. Performance of the proposed CNN-ET-LSTM network

Performance Matrices	Number of epochs = 60	Number of epochs = 80	Number of epochs = 100	Number of epochs = 120
Accuracy (%)	97.52	97.21	97.18	96.72
Precision (%)	97.80	97.73	97.40	97.48
Recall (%)	97.52	97.20	97.17	96.71
F1-score (%)	97.62	97.39	97.25	96.97

(a)

(b)

(c)

(d)

(a)

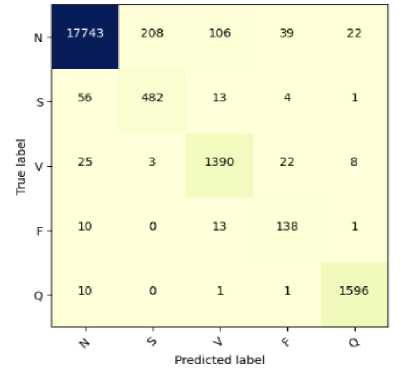
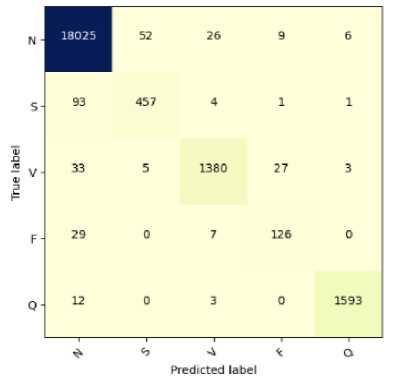
Fig.11. Confusion matrix for ECG arrhythmia classification based on proposed CNN-ET-LSTM network (a) with SMOTE (b) without SMOTE

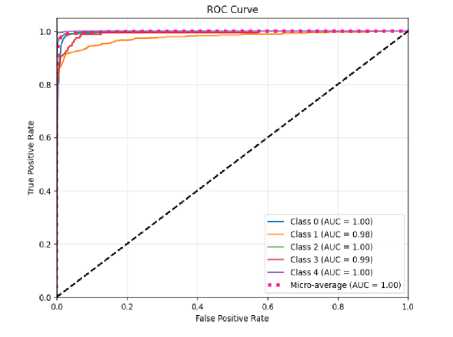
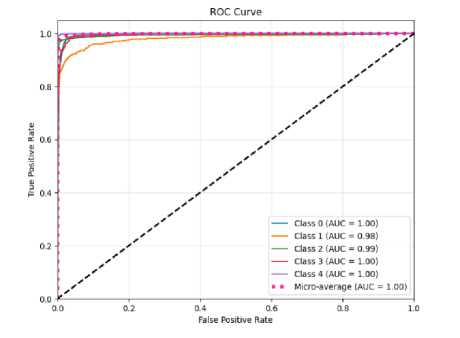
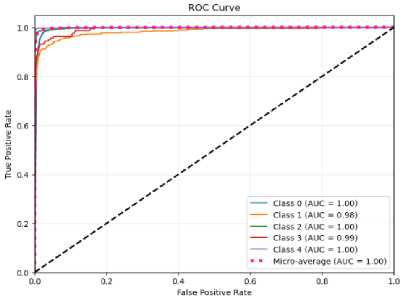
Fig.10. The ROC curve of the proposed CNN-ET-LSTM network with different number of epochs (a) 60 (b) 80 (c) 100 and (d) 120

(b)

We have conducted a performance comparison analysis among the proposed model and the related published works with similar data. It should be mentioned that the test data size of this study is 20% of the original raw data, which is larger comparing many related studies. The proposed system comparatively performs better in terms of different performance indices as shown in Table 5. The systems [8, 31, 34] have moderately higher performance. Proposed system of Xue et al. [11] exhibits significant performance parameters with the accuracy of 95.90%, precision of 96.34%, recall of 95.90%, and F1-score 95.92%. As shown in the table, the value of these parameters of our proposed system are 97.52%, 98.80%, 97.52%, and 97.62% respectively which is better than mentioned related systems. Therefore, the proposed model could be an effective tool for classifying heart abnormalities and be a better solution to this five-class classification problem.

Table 5. Performance comparison of the proposed system with related works

Reference	Architecture	Classes	Accuracy (%)	Precision (%)	Recall (%)	F1-score (%)
Acharya et al. [8]	1D-CNN	5	94.03	-	96.71	-
Xue et al. [11]	CNN-BiLSTM	5	95.90	96.34	95.90	95.92
Kachuee et al. [34]	1D-CNN	5	93.42	94.30	93.42	93.43
Pyakillya et al. [35]	1D-CNN	4	88.52	91.35	88.52	88.58
Milad et al. [36]	2D-CNN	4	89.04	89.43	89.33	88.85
Zhu et al. [37]	CNN-FWS	2	90.05	-	88.90	90.20
Proposed Work	CNN-ET-LSTM	5	97.52	97.80	97.52	97.62

5.    Conclusions

Cardiac arrhythmia is a global health concern as it can affect people of all ages and all over the world especially where the healthcare resources are limited. Therefore, automatic detection and classification of ECG arrhythmia hold immense significance globally. We propose a novel deep CNN-ET-LSTM model to automatically categorize five distinct types of arrhythmias. The database used in this research work is the renowned MIT-BIH arrhythmia dataset which have noise inherently because the collect from real-world as well as have the power line interference and motion artifacts. This makes the dataset more realistic and demonstrates the model robustness. SMOTE is used to composure the problem caused by class imbalance of train data that helps better performance on classes with the least number of instances. The proposed system shows the accuracy of 97.52%, precision of 97.80%, recall of 97.52% and F1-score of 97.62% with raw blind test data. With applying SMOTE, the proposed system showed better performance on class S, V, F and Q but lower performance on normal class. As future perspective, we will consider adding other significant classes of arrhythmias, using different arrhythmia dataset, more suitable balancing technique and varying the number of CNN layers of the model in real world noisy environment. We are planning to develop hardware prototype to deal with real life clinical applications. These would be contemplated in future work. Overall, the proposed model can be used for clinical applications toward better cardiac healthcare.