Начально-краевая задача электродинамики для дефектного ферритового тела

Начально-краевые задачи электродинамики, не предполагающие сокращающуюся гармоническую зависимость электромагнитного поля от времени, необходимы как для общего описания, так и для конкретных расчетов нестационарных электромагнитных полей. Нестационарные электромагнитные поля возникают в электротехнических установках при переходных процессах; также они используются в неразрушающем контроле проводящих изделий [1]. С этим обстоятельством связана актуальность исследования начально-краевых задач электродинамики, в том числе в проводящих магнитных средах. В частности, необходимо доказывать существование и единственность решения таких начально-краевых задач, это служит базой для численных методов.

Ранее широко исследовались внутренние начально-краевые задачи электродинамики для ограниченных областей [2; 3]; наиболее существенные результаты были получены для областей с границами класса С ^{( 2 )} [3]. Однако в электротехнике и особенно в неразрушающем контроле актуальны не только внутренние начально-краевые задачи, но также и задачи сопряжения, в постановке которых граничные условия связывают поле снаружи проводящего тела с полем внутри тела: именно эта связь (безусловно, физически реальная) делает неразрушающий контроль возможным, позволяет судить о внутренней структуре проводника по внешнему полю.

Начально-краевые задачи сопряжения для магнитных сред были рассмотрены ранее применительно к дефектному ферромагнитному металлу [4] и магнитному диэлектрику, имеющему структурные нарушения [5]. Однако в электротехнических устройствах используются также ферриты, представляющие собой магнитные полупроводники. Ферритовые сердечники в трансформаторах, дросселях и иных стабилизирующих устройствах регулярно подвергаются воздействию нестационарных электромагнитных полей при случайных изменениях силы тока в обмотках; кроме того, феррит может быть целенаправленно подвергнут воздействию нестационарного электромагнитного поля для выявления его структурных нарушений [1].

Таким образом, исследования начально-краевых задач сопряжения применительно к ферритовым телам актуальны; в частности, актуально доказательство существования и единственности решения этих задач.

• 1    Постановка задачи

Для множества вещественных чисел примем стандартное обозначение R . Соответственно, трехмерное геометрическое пространство отождествим с декартовой степенью R³. Упорядоченный набор трех пространственных координат точки будем обозначать r .

Предположим, что феррит занимает ограниченную область Ос R³; граница области О представляет собой кусочно-гладкую поверхность. Дефектные области О , , О₂,...,О k имеют кусочно-гладкие границы; замыкания этих областей включаются в О и не пересекаются: О i сО , О i п О j = 0 при i * j .

Ферриты представляют собой магнетики с магнитной проницаемостью ц, существенно превосходящей 1. В то же время ферриты являются полупроводниками. То есть в этих материалах наличествуют как свободные электроны, благодаря которым феррит обладает ненулевой электропроводностью о, так и связанные электроны, обеспечивающие во внешнем электрическом поле поляризацию достаточно сильную, чтобы диэлектрическая проницаемость ферритов е существенно превышала 1.

К дефектам приводят технологические недочеты изготовления ферритов: неравномерное перемешивание шихты — смеси порошков исходных оксидов, из которых изготовлен феррит; последующее некачественное прессование и спекание порошков. В результате этих недочетов и возникают дефектные области, на границе которых электрические и магнитные свойства ферритов резко, скачкообразно изменяются. Это проявляется в координатной зависимости электропроводности, диэлектрической и магнитной проницаемости феррита.

В рамках рассматриваемой задачи примем естественное предположение, что электропроводность, диэлектрическая и магнитная проницаемость феррита не зависят от времени. Как функция пространственных f k ^

координат о ( r ) > 0, непрерывна в областях Q i и Q \ I uQ i I , причем мо-

\ i=1       / жет быть непрерывно продолжена с каждой из этих областей на ее границу, оставаясь при этом положительной. Кроме того, е(r)> 1, ц(r)> 1, причем функции е(r) и ц(r) непрерывны в Qi и Q \fuQi J и также допускают непрерывное продолжение с каждой из этих областей на границу, оставаясь при таком продолжении больше 1. При переходе же через границы Qi функции о(r), е(r) и ц(r) терпят разрыв. Снаружи ферритового тела, то есть в точках, внешних по отношению к Q, о( r ) = 0 и е( r ) = ц( r ) = 1.

Будем предполагать, что сторонний ток сосредоточен в ограниченной области T ; замыкания областей Q и T не пересекаются: Qn T = 0 . Как функция пространственных координат r и времени t , плотность стороннего тока J ( r , t ) дважды непрерывно дифференцируема при r е T и t >  0; кроме того, J ( r ,0 ) = 0 ( 0 — обозначение нулевого вектора). В точках, внешних по отношению к T , J ( r , t ) ^ 0 .

Электромагнитное поле внутри и снаружи ферритового тела удовлетворяет системе уравнений Максвелла:

d E

5t dH d t

е0е( r )

о ( r) rot H --У- E

е0е( r)

—

е0е( r )

,

Ц д Ц ( r )

rot E

где E и H — соответственно напряженности электрического и магнитного поля; е ₀ и ц ₀ — соответственно диэлектрическая и магнитная постоянные.

В точках гладкости границ областей Qi и О электромагнитное поле удовлетворяет условиям сопряжения для двух сред, не являющихся иде альными проводниками:

F . = F

E T ,int     E T ,ext

,

• ¹¹    T,int    ¹¹ T,ext

где индекс т обозначает касательную компоненту вектора; int и ext — обозначение предела соответственно изнутри и снаружи области.

Электромагнитное поле в начальный момент времени t = 0 определя- ется начальными условиями:

E ( r ,0 ) = E о ( r ) H ( r ,0 ) = H о ( r ) .

Начальное магнитное поле должно удовлетворять условию div(p(r)H0 (r)) = 0, где частные производные, входящие в дивергенцию, в общем случае следует понимать как обобщенные. Заметим, что в силу уравнений (1) выполнение этого тождества для магнитного поля при t = 0 влечет за собой его выполнение при t > 0 [4; 6]. В остальном выбор E 0 ( r ) и H0 (r) может быть произвольным в рамках функционального класса, определяемого для постановки задачи.

Для решения задачи (1)-(3) функциональный класс выберем следующим образом. В любой фиксированный момент времени t > 0 векторные поля E (r, t) и H (r, t) должны принадлежать пространству H (rot,R3) — пространству векторных полей, квадратично суммируемых в R3 вместе со своими обобщенными роторами [3-5]. Кроме того, при t > 0 E (r, t) и

H (r, t) должны быть дифференцируемы по времени в смысле сходимо- сти по среднеквадратичной норме в R 3 :

E (r, t + At)-E (r, t) A t

- ^E' , ( r - t )

^ 0,

A t ^ 0

H (r, t + A t)-H (r, t) A t

- h;( r, t)

^ 0,

A t ^ 0

где индекс 2 означает среднеквадратичную норму на R3 .

Покажем, что в такой постановке у начально-краевой задачи (1)-(3) существует единственное решение, непрерывно зависящее от начальных условий.

2 Основные теоремы

Для исследования начально-краевой задачи (1)-(3) проведем исследование свойств дифференциального оператора Ji, который на каждую упорядоченную пару векторных полей (u;v)е(H(rot,R3)) действует следующим образом:

_х f 1          ^         1        )

A ( u ; v ) = —rot v--u ;-- rot u I .

sns

£0£

ЦдЦ

Для того чтобы сформулировать свойства пространства H ( rot,R³ ) и оператора A , введем следующие обозначения. H ' — пространство непрерывно дифференцируемых в R³ векторных полей, квадратично суммируемых вместе со своими роторами. K — пространство векторных f k ^ полей, непрерывно дифференцируемых в областях Q i , Q \ I uQ i I и

I i = 1         /

R³ \ Q , допускающих непрерывное продолжение вместе со своими производными с каждой из этих областей на ее границу, удовлетворяющих граничным условиям вида (2) и, кроме того, квадратично суммируемых в R³ вместе со своими роторами. L ₂ — пространство векторных полей, квадратично суммируемых на множестве, указанном в скобках после L ₂ .

A

A

A' — дифференциальный оператор, действующий, как и оператор A , по формуле (4), но на меньшем пространстве K .

Ранее была доказана серия теорем, касающихся H ( rot,R³ ) [4].

Теорема 1. Н ’с K с H ( rot,R³ ) с L ₂ ( R³ ) , причем H ' — плотное подпространство L ₂ ( R³ ) .

Теорема 2. Если последовательности u n е H ( rot,R³ ) и rot u n сходятся по норме L ₂ ( R³ ) , соответственно к u и v , то u е H ( rot,R³ ) и v =rot u .

Теорема 3. Для любого векторного поля u е H(rot,R3) существует последовательность un е H', сходящаяся по норме L2 (R3) к u, для ко- торой rotun сходится к rotu .

Воспользовавшись теоремами 1-3, можно доказать следующую теорему.

Теорема 4. Оператор A имеет плотную в ( L ₂ ( R ) ) область определения и является минимальным замкнутым расширением оператора J 1' .

Ранее аналогичное свойство оператора J 1 было доказано для случаев ферромагнетика [4] и магнитодиэлектрика [5]. В рассматриваемом случае дефектного ферритового тела имеет место иной характер зависимости коэффициентов в выражении (4) от пространственных координат, так как электрические и магнитные свойства предполагаются уже другими. Однако рассуждения, методы и приемы, с помощью которых доказывается теорема 4, совершенно аналогичны тем, которые были использованы ранее; поэтому теорему можно принять как уже доказанную.

Теорема 4 обосновывает выбор пространства

H ( rot,R 3 ) для поста-

новки исследуемой начально-краевой задачи: оператор Aˆ является минимальным замкнутым расширением оператора A‘, в то время как A‘ определен на пространстве K , учитывающем граничные условия задачи. При этом основные теоремы, касающиеся существования и единственности решения задачи Коши в абстрактном нормированном пространстве, доказаны исключительно для замкнутых операторов [1].

Теорема 5. Для любой упорядоченной пары (f,g)e(L2(R3)) и для любого p > 0 у уравнения A(u;v)-p•(u;v) = ( f;g) в пространстве

( H ( rot, R³ ) ) 2

существует единственное решение. Это решение удовле- творяет неравенству

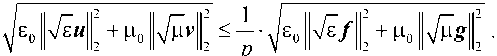
Доказательство. Рассматриваемое уравнение с оператором шем в эквивалентной форме:

A запи-

J-rotv + o( r) u + e0 p e( r) u = -e0e( r) f (r) trotu + Цо p p( r) v = -RoR( r) g (r)         .

Для полей u , v e H ( rot,R³ ) справедливо следующее равенство [4]:

J ( v ( r ) rot u ( r ) - u ( r ) rot v ( r ) ) dV = 0 .                  (7)

R3

Путем умножения первого и второго уравнения системы (6) соответственно на u и v , последующего сложения уравнений и интегрирования по R³ , в силу (7), получаем равенство

£ o p || Vs u |₂ + Ц о p|| W ^v ||₂¹ J^( ^r ) u ( ^r )|^{2 dV} =

о

^-e o J ^e ( ^r ) ^f ( ^r ) ^u ( ^r ) ^{dV -} P o j p ( ^r ) g ( ^r ) v ( ^r ) ^dV .

R ³

R ³

В полученном равенстве учтено, что о ( r ) ^ 0 только в О . Заметим, что левая часть полученного равенства неотрицательна. Следовательно, в силу неравенства Коши — Буняковского для интегралов и сумм,

e0p|| Vsu |2 +Р0 p|| W v||2 + J^( r ) u ( r )|2 dV =

о

e0 J s(r) f (r)u(r)dV + P0 J p(r)g(r)v(r)dV

R3R3