Наглядность как один из методов активизации познавательной деятельности в процессе изучения математики

EDN: DQMUQV

Введение. Наглядность – это один из принципов обучения. Под наглядностью понимают свойство, которое выражает степень доступности и понятности психических образов объектов познания для познающего субъекта.

Целью данного исследования является определение возможностей применения наглядных методов обучения для повышения уровня познавательной деятельности студентов в процессе изучения дисциплины «Математика» на экономических специальностях.

Объект исследования – процесс обучения математике студентов экономических направлений и специальностей в вузе. Предметом же служат содержание, методы и формы изучения математики с использованием наглядных представлений решений задач профессионально направленного содержания.

Методы исследования. Для достижения поставленной цели потребовалось решить следующие задачи:

• -    провести анализ теоретических и методических аспектов наглядности в педагогической и методической литературе;

• - разработать технологию обучения математике с использованием наглядных методов для обучающихся экономического профиля;

• -    определить особенности применения метода наглядности при решении математических задач;

• -    привести примеры использования метода наглядности для решения некоторого класса задач экономического содержания;

• - на практических занятиях по математике проверить эффективность использования метода наглядности в усвоении учебного материала обучающимися;

Для решения поставленных задач рассматриваемого данного исследования произведен анализ дидактической, психологической, методической литературы, в том числе учебно-методических пособий по математике для обучающихся экономического профиля, а также эмпирическое наблюдение за усвоением учебного материала с использованием наглядных методов при решении профессионально-направленных задач.

История вопроса. Для начала следует учесть принцип полезности, предполагающий отбор только того учебного материала, который имеет для обучающихся практическую ценность. Кроме того, необходимо обеспечить энциклопедичность и взаимную связность знаний, при этом информация представляется в виде целостной системы. Бесспорно, следует стремиться к чёткому разграничению знаний в темах и материалах. Это необходимо, чтобы обучающиеся имели возможность лучше понять и усвоить информацию. Самую важную роль играет последовательность в обучении, так как новые знания должны опираться на ранее полученные. Ещё один важный момент заключается в том, что взаимосвязанные темы рекомендуется изучать одновременно, что способствует улучшению понимания изучаемого материала. Усвоенные знания должны надолго оставаться в памяти, для этого следует уделять внимание стимуляции самостоятельного мышления обучающихся и развитию их способностей. Необходимо найти баланс между памятью, разумом и речью, чтобы знания были не только усвоены, но и легко воспроизводимы вербально. Особое внимание следует уделять повторению изученного материала и применению его на практике в целях закрепления полученных знаний. То есть соблюдение дидактических принципов и применение рациональных методов обучения выступают в качестве основных условий эффективной организации учебного процесса. Классики мировой и отечественной педагогики – И.Г. Песталоцци, Я.А. Коменский, А. Дистервег, Дж. Локк – считали, что принцип наглядности обучения является одним из основополагающих в дидактике. Работы В.П. Беспалько, Н.М. Шахмаева, В.Г. Болтянского1 и др. посвящены разработке теоретических положений и условий применения средств наглядности в процессе обучения. Теоретические положения и условия применения средств наглядности нашли свое отражение в публикациях Ю.О. Овакимяна, И.А. Зимней, И.С. Якиманской, М.А. Холодной, С.И. Архангельского2 и др. В России педагогами с конца восьмидесятых годов прошлого века начинают осваиваться и применяться активные методы обучения [Гаджиев М. Ш., с. 19]. Такие психологи, как В.В. Давыдов, П.Я. Гальперин, Р. Арн-хейм, В.П. Зинченко3 и др., описали особенности зрительного восприятия знаковой информации. Принцип наглядности нашёл своё применение в практике преподавания различных дисциплин. Од- ной из таких дисциплин является математика. Наглядность помогает обучающимся сформировать первое представление о предмете, а затем развить способность логического мышления и закрепить полученные знания. В целях подготовки обучающихся к реальной трудовой деятельности, следует связать в их сознании понятия и выводы с понятными образами соответствующих объектов [Знаенко Н.С., с. 10].

Использование наглядности в процессе обучения принесёт положительные результаты, если с её помощью обучающиеся смогут выделить и осмыслить главные характеристики объектов и предметов.

• •    Натуральная (естественная) наглядность основывается на непосредственном взаимодействии с реальностью, что обеспечивает максимальную достоверность представления материала.

• •    Изобразительная наглядность – методика визуальной демонстрации. Этот метод предполагает показ видимых образов: плакатов, карт, портретов, моделей, изображений и символов, опытов, технических установок, также сюда относятся презентации, кино/видео материалы и т. п.

• •    Символическая наглядность – широко применяется в обучении математики: чертежи, графики, схемы, таблицы, она помогает работать с абстрактными понятиями, преобразовывать их и применять. Наглядность в обучении математики можно поставить на первое место, так как она способствует облегчению процесса усвоения знаний и развитию критического мышления, а также обеспечивает творческий подход к решению задач [Миракова Т.Н., с. 28]. Современные образовательные технологии значительно расширяют возможности использования наглядности [Максименко Н.В., с. 3119]. Цифровые платформы, такие как Moodle или GoogleClassroom, интерактивные доски, виртуальная и дополненная реальность позволяют создать динамические и интерактивные образы, которые усиливают образовательный эффект. В связи с этим именно при изучении математики принципы наглядности находят весьма широкое применение. Они играют ключевую роль в повышении качества усвоения новой информации, развитии умственных способностей обучающихся и расширении педагогических возможностей преподавателя.

Основная задача наглядности заключается в генерации актуальных знаний на базе имеющегося опыта. Образное мышление способствует формированию оригинальных концепций через анализ накопленной информации [Пономарева С.Я., с.195].

Креативный подход к рассмотрению графических материалов содействует решению математических задач и уравнений. Образное восприятие благоприятно влияет на обучение и снижает психологическое напряжение. Эффективное применение визуального метода требует регулярных тренировок и развития творческого потенциала.

Наглядность, будучи фундаментальным принципом обучения, активизирует мыслительную деятельность, память и воображение. Образы объектов становятся наглядными только при их осмыслении и сопоставлении с имеющимися знаниями. При этом формируется целостность восприятия учебного материала, что делает процесс обучения более глубоким и эффективным. Интеграция современных технологий с традиционными методами обучения позволяет максимально использовать потенциал наглядности для формирования профессиональных компетенций.

Математические концепции тесно переплетаются с визуальными представлениями. Базовые понятия (расстояние и числовые вычисления) берут начало из реальных ситуаций. Это определяет значимость наглядности при изучении и преподавании математических дисциплин [Худенко В.Н., с. 368].

Визуальный подход к обучению помогает раскрыть взаимосвязи математических объектов. Человеческое мышление опирается на образное восприятие, поэтому инструменты наглядного метода эффективны не только при решении геометрических задач, но и при решении задач из других разделов математики [Белов С.В., c.18].Например, в алгебраических вычислениях и статистическом анализе диаграммы демонстрируют корреляции между параметрами, а графическое отображение информации помогает обнаружить закономерности и отклонения. При изучении сложных разделов (теории чисел или математического анализа) преподаватели активно применяют схемы, рисунки и условные обозначения для упрощения восприятия материала [Попова И.А., с. 67].

Визуализация математических концепций расширяет горизонты познания и делает учебный материал доступнее. Если при взаимодействии педагога с аудиторией возникают сложности в восприя- тии информации, наглядность помогает преодолеть эти преграды. Внедрение визуальных элементов требуется начинать на начальном этапе образовательного процесса. Данная задача сопряжена с серьёзными трудностями, поскольку развитие образного мышления происходит постепенно. Педагоги при использовании наглядности сталкиваются с рядом затруднений. Основные сложности связаны с подбором эффективных инструментов и адаптацией методик под индивидуальные особенности обучающихся. Главная цель применения наглядности – увеличение интереса к дисциплине и улучшение качества усвоения материала. При отсутствии положительного эффекта от визуализации её интеграция в образовательный процесс теряет смысл.

Следует отметить, что вопросы совершенствования математической подготовки студентов, в частности, использование наглядных методов в процесс обучения, по-прежнему актуальны и рассматриваются в работах многих учёных, где описаны разные педагогические подходы к изучаемой проблеме [Борбоева Г.М., с. 54]. Например, исследования А.С. Гребенкиной показали, что для визуализации целесообразно в процессе математической подготовки студентов технических специальностей использовать автоматизированные компьютерные системы [Гребенкина А.С., с. 178].

В настоящей же работе предлагается рассмотреть применение наглядного метода обучения дисциплине «Математика» для обучающихся экономических направлений и специальностей Приволжского государственного университета путей сообщения и представить некоторые аспекты, связанные с построением курса математики с учётом особенностей мышления обучающихся.

Материалы исследования. Знакомство с задачами экономического содержания у обучающихся начинается при сдаче единого государственного экзамена по профильной математике в 11 классе. Как правило, подобные задачи общепринято решать с помощью наглядных методов обучения, например, с помощью составления таблицы, или как мы предлагаем решать такие задачи, используя принцип наглядности «кирпичи в аренду» (рис. 1).

В вузе задачи экономического содержания рассматриваются в разных разделах математики. Принцип наглядности целесообразно использовать при решении, например, задач, предполагающих построения математических моделей. В качестве примера рассмотрим решение задачи линейного программирования графическим методом.

Задача : для изготовления двух видов продукции А 1 и A 2 используют три вида ресурсов B 1 , B 2 и B 3 . Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции и прибыль, получаемую от реализации единицы продукции A 1 и A 2 , заданы в таблице 1.

Таб. 1 . Запасы ресурсов, число единиц ресурсов и прибыль, получаемая от реализации единицы продукции (Resource stocks, the number of resource units and the profit earned from the sale of a unit of production)

	В 1	В 2	В 3	Прибыль
А 1	7	4	3	12
А 2	8	9	1	10
Запасы	474	396	174

Необходимо составить такой план производства продукции, при котором прибыль от её реализации будет максимальной.

Составим систему ограничений для х 1 -числа единиц продукции A 1 и х 2 - числа единиц продукции A 2 , запланированных к производству.

'7 X j + 8 x ₂<  474

4 x i + 9 x 2 <  396

<3Xj + x2 < 174

• ^X i >  0

Lx2 > 0

при этом функция Z = 12 х 1 +10 х 2 должна принимать максимальное значение.

Рис. 1 . Пример решения задачи с помощью наглядных методов обучения (An example of a solution using visual learning methods)

Сначала найдём множество решений системы неравенств. Рассмотрим 1-е неравенство и заменим его точным равенством 7х1 + 8х2 = 474. Это уравнение прямой в плоскости х1Ох2. Строим ее по двум точкам: (0;59,25) и (67  ;0)

Так как точка О (0;0) удовлетворяет первому неравенству

7х1+8х2≤474(7·0+8·0≤474), то и все точки полуплоскости, на которые прямая 7х1+ 8х2= 474 делит плоскость х1Ох2 и которая содержит точку О (0; 0) будут также удовлетворять первому неравенству. Аналогично находим решение всех остальных неравенств и пересечение всех полуплоскостей, определяющих множество решений системы ограничений. Это будет выпуклое множество – многоугольник ОАВСД.

Пусть Z= 120, тогда прямая будет иметь вид :12 x 1 +10 x 2 =120. Далее найдём координаты вектора.

gradZ =

'dZ d Z

I ;л dXj  dx2

, следовательно, gradZ = {12;10}.

Построим этот вектор на координатной плоскости (рис. 2). Так как в направлении вектора grad Z функция Z возрастает, а в противоположном направлении убывает, то, перемещая прямую Z = 120 в направлении grаd Z, мы будем переходить от меньших значений Z к большим.

Рис.2 . Графический метод решения (Graphical solution method)

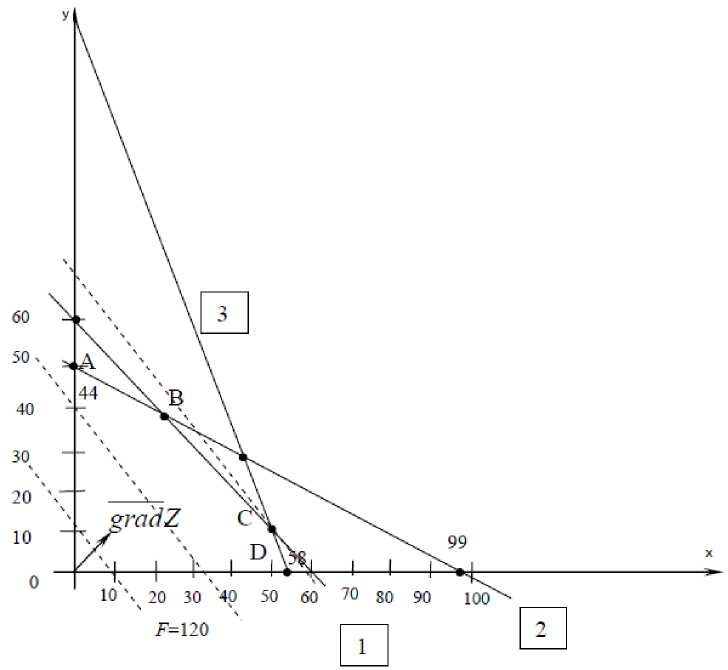
Точка С области ОАВСД наиболее удалена от начала координат в направлении grаd Z. Следовательно, в этой точке функция Z имеет наибольшее значение. Решая систему уравнений прямых 1 и 3, найдём координаты точки С.

'7 % ! + 8 x₂ = 474    ' 7 X j + 8 x₂ = 474

^1

3 X j + x₂ = 174      I x₂ = 174 — 3 X j

> I

'7 x + 8(174 — 3 X !) = 474

_ X₂ = 174 - 3 X j

>

'7 X j + 1392 — 24 X j = 474    '— 17 X j = — 918

1                                                >;

X₂ = 174 — 3 X j              | X₂ = 174 — 3 X j

> I

L ^X 2

= 54

= 12

Подставим найденные координаты точки С в функцию Z.

Итак, Zmax = Z ( C ) = Z (54;12) = 12·54+10·12 = 768.

Можно сделать вывод, что продукции вида А 1 следует производить 54 ед., вида А 2 –12 ед., при этом максимальная прибыль от реализации составит 768 ед.

Предложенным методом данная профессионально направленная задача решается при изучении дисциплины «Математика» в разделе «Аналитическая геометрия на плоскости».

Рассмотрим симплекс метод решения этой же задачи. Расширенная система задачи имеет вид:

7 x₁ + 8 x ₂ + x₃ = 474

< 4 x + 9 x ₂ + x₄ = 396

3 Xj + x2 + x5 = 174

Заносим её в исходную симплекс-таблицу (рис. 3).

Рис. 3 . Начальная симплекс-таблица (The initial simplex table)

[12     10 О О 0

Б	СЕ	^1		^3		^5	в	61
^3	0	7	8	1	0	0	474	67^
---	0	4	9	0	1	0	396	99
	0		1	0	0	1	174	58
Аг		-12	-10	0	0	0	0

Последний столбец подготовлен для оценочных отношений, необходимых при расчёте наибольшего возможного значения вводимой в базис переменной. Последняя строка таблицы является строкой оценок разложения векторов условий по базису опорного решения. Оценка разложения вектора условий A j по базису опорного решения находится по формуле

m

• A,. = YC^x. - c, j               Б ij        j

i =1

В последней строке таблицы с оценками в столбце "B" записываем значение целевой функции на начальном опорном решении Z(X 0 ):

m

Z ( X _o) = ^ C_Bb_i = 0 • 474 + 0 • 396 + 0 - 174 = 0.

i =1

Начальное опорное решение не является оптимальным, так как оценки Aj = - 12, A₂ = - 10 для векторов-условий А 1 и А 2 противоречат признаку оптимальности (в задаче на максимум все оценки должны быть неотрицательными).

Вводим в базис вектор с наибольшей (по модулю) отрицательной оценкой, т.е. вектор А 1 .

Выводим из базиса вектор с минимальным оценочным отношением для первого столбца. Вы числяем оценочные отношения ^^ = -1-.

^ai 1

Минимум оценочного отношения 0 i 1 достигается в третьей строке:

^ = min

474 396 1741        Г 5

----,---,      = min 67 —,99,58

7     4     3 I          I 7

Следовательно, выводим из базиса вектор A 3 . Выполняем преобразование Жордана-Гаусса с разрешающим элементом a 13 =3:

Рис. 4 . Вторая симплекс-таблица (The second simplex table)

12 ЦО О О О

Б	СБ	41	4.	4S	4д	45	41	01
43	0	0	17/ /з	1	0	-7/ /з	68	12
44	0	0	23/	0	1	-4/ /з	164	~ /23
41	12	1	и / 3	0	0	1/ /3	58	174
Аг		0	-6	0	0	4	696

Получаем второе опорное решение X=(58, 0, 68, 164,0) с единичным базисом Б=(A 1 ,A 3 ,A 4 ). Оценки разложения векторов - условий по базису опорного решения находим аналогично 1-му шагу.

Полученное решение не является оптимальным, т.к. вектор A 2 имеет отрицательную оценку

Д2 = -6.

Для улучшения решения вводим в базис вектор A 2 . Вектор, выводимый из базиса, определяем по минимуму оценочного отношения для второго столбца:

= min <

68  164  58

= mn 12,21 —,174

I       23

= 12.

Т.е. выводим из базиса вектор А 3 . Выполняем преобразование Жордана-Гаусса с разрешающим элементом a 12 =17/3 (рис. 5):

Рис. 5 . Третья симплекс - таблица (The third simplex table)

Б	С’Б	^1	^2	^3	Л	^5	^i
^2	10	0	1	з/ /17	0	-7/ /17	12
	0	0	0	_23/ /17	1	31/ /17	72
^1	12	1	0	_ 1/ /17	0	8/ /17	54
А»		0	0	18/ /17	0	26/ /17	768

Получение решение X* = (54, 12, 0, 72,0) является оптимальным, т.к. для всех векторов – условий, не входящих в базис, оценки положительные. Значение целевой функции при этом равно Z(X*) = 768.

Симплекс-методом данная задача решается при изучении дисциплины «Математика» в разделе «Линейная алгебра». Таким образом, одна и та же профессионально направленная задача решается с помощью двух различных наглядных методов, затем при изучении раздела «Дифференциальное исчисление функций нескольких переменных» данная задача решается аналитическим методом.

Результаты исследования. В результате проведённого исследования определён концептуальный подход к обучению математике для студентов экономического профиля, основанный на использовании наглядного моделирования учебного материала. Обучающиеся учатся строить математические модели, овладевают математическими приёмами и методами решения поставленных задач, при этом накапливаются математические знания, необходимые выпускникам для решения задач уже в будущей профессиональной деятельности [Архипова Н.А., а)], [Архипова Н.А., б)].Кроме того, используя в процесс обучения математике наглядные методы, мы способствуем тому, что у обуча- ющихся развивается логическое мышление, повышается познавательная активность и мотивация к изучению дисциплины. Практическая значимость данного исследования заключается в том, что предложенные подходы (наглядные методы решения экономических задач) могут быть использованы в процессе обучения математике учащихся школ и студентов экономических направлений и специальностей вузов.

Выводы. Таким образом, в данной статье представлена специфика применения наглядных методов в организации учебного процесса. Кроме того, продемонстрировано, как методы наглядности работают при изложении изучаемого материала по математике. Опыт показывает, что решения задач, представленные в виде таблиц, схем или рисунков, дают лучший результат в усвоении математики обучающимися.