Напряженно-деформированное состояние двутавровой балки с дефектом стенки в виде круглого выреза

Применение двутавровых балок широко распространено в строительстве. Двутавровая балка имеет оптимальное сечение при работе на изгиб за счет максимального удаления материала от центра тяжести, что значительно повышает момент сопротивления.

В настоящее время имеется некоторое количество работ, посвященных расчету двутавровых балок с круглыми вырезами по всей длине балки. Наиболее распространены работы А.С. Притыкина и А.И. Лавровой [1-4], А.И. Мишичева [5]. Результаты этих работ справедливы для балок со строго выраженной симметрией.

Актуальность данной работы заключается в рассмотрении влияния одиночного круглого выреза, расположенного на разных расстояниях от торца балки, что создает отсутствие симметрии дефекта относительно центра балки. Как известно, наличие отверстий, выступов, углублений и других резких изменений геометрии создает «очаги» концентрации напряжений вследствие резкого изменения направления и сгущения потоков силовых линий [6].

Целью данной работы является моделирование двутавровой балки с отверстием в стенке в программном комплексе ANSYS и анализ напряженно-деформированного состояния при расположении отверстия на разном расстоянии от опоры.

В качестве сечения балки использован двутавр 40Б1 по ГОСТ Р 57837-2017 длиной 6 м, выполненный из стали класса С345. Твердотельное моделирование двутавровой балки без дефектов и с отверстием в стенке двутавра выполнено в AUTOCAD . Размер круглого выреза стенки принят диаметром 112 мм. Произведено рассмотрение четырех вариантов балок: без дефекта, а также с дефектом в виде круглого выреза на расстоянии 0,5, 1,5, 3,0 м от опоры. Схема балки с вырезами изображена на рисунке 1.

Решение задачи выполнено с учетом физической нелинейности материала (задана билинейная модель с изотропным упрочнением для стали С345) и геометрической нелинейности (учет больших перемещений функцией Large Deflection ). Опирание балки осуществлено на участки длиной 200 мм (моделирование колонны), поэтому длину балки увеличим на 200 мм с каждой стороны. При таком методе решения заданный пролет сохраняется, но опорные участки решаются более приближённо к действительности.

*    - 1 образец без круглого быреза

4------ ^------ , 500	30 1500	00
	) 2образец              (	) 3 образец                            (	j 4 образец
V------		6000

Рис. 1. Схема балки с вырезами

В качестве закреплений применены шарнирно-неподвижные опоры (Displacement), ограничивающие перемещения по всем осям, но позволяющие поворот. В качестве загружения на балку задана нагруз- ка, распределенная на площадь верхнего пояса P = 0,242 МПа и собственный вес балки. Расчетная схема для второго образца (отверстие на расстоянии 0,5 м от опоры) изображена на рисунке 2.

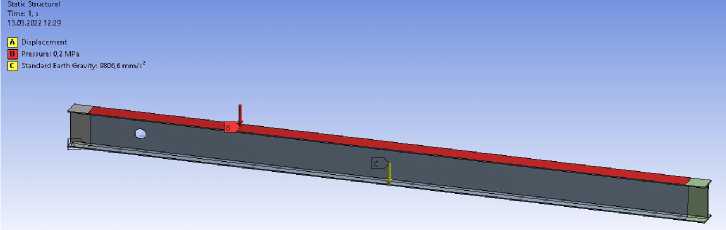
Рис. 2. Расчетная схема для балки с отверстием на расстоянии 0,5 м от опоры

По результатам расчета получены следующие вертикальные перемещения (прогибы): для балки без дефектов (рис. 3), для балки с отверстием в стенке на расстоянии 0,5 м от опоры (рис. 4), для балки с отвер- стием в стенке на расстоянии 1,5 м от опоры (рис. 5) и для балки с отверстием в стенке на расстоянии 3,0 м от опоры (рис. 6).

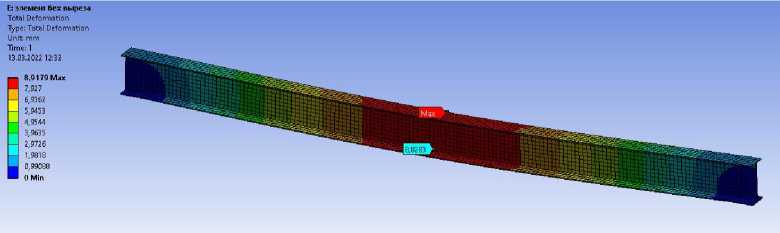
Рис. 3. Значения вертикальных перемещений двутавровой балки без дефектов

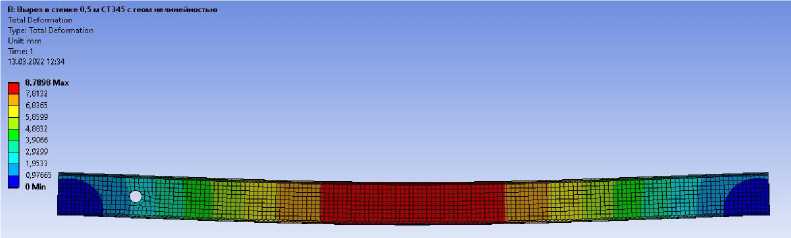
Рис. 4. Значения вертикальных перемещений двутавровой балки с круглым вырезом на расстоянии 0,5 м от опоры

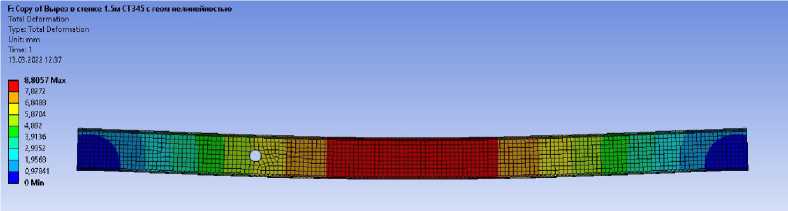
Рис. 5. Значения вертикальных перемещений двутавровой балки с круглым вырезом на расстоянии 1,5 м от опоры

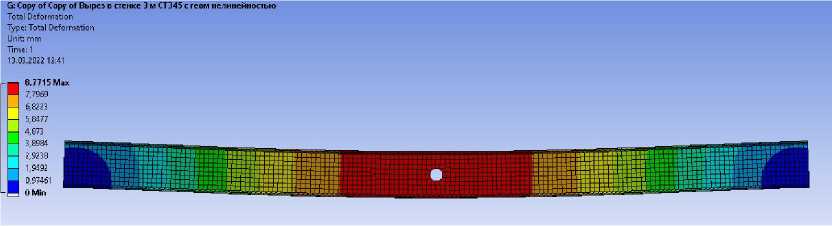
Рис. 6. Значения вертикальных перемещений двутавровой балки с круглым вырезом на расстоянии 3,0 м от опоры

Установлено, что в целом наличие круглого выреза в стенке балки не оказывает существенного влияние на изменение максимального значения перемещений (вертикальных прогибов).

По результатам расчета также получены следующие эквивалентные напряжения для балки без дефектов (рис. 7), для балки с отверстием в стенке на расстоянии 0,5 м от опоры (рис. 8), для балки с отверстием в стенке на расстоянии 1,5 м от опоры (рис. 9) и для балки с отверстием в стенке на расстоянии 3,0 м от опоры (рис. 10).

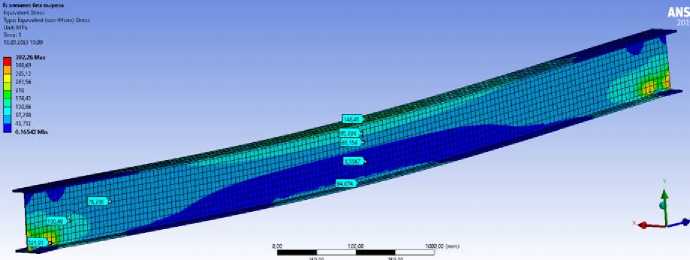
Рис. 7. Эквивалентные напряжения в балке без дефектов

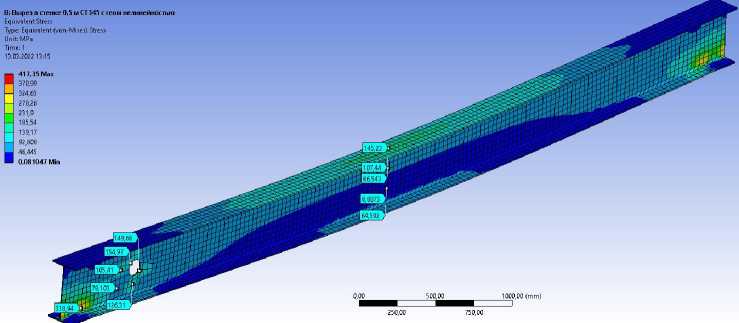
Рис. 8. Эквивалентные напряжения в балке с круглым вырезом на расстоянии 0,5 м от

опоры

Рис. 9. Эквивалентные напряжения в балке с круглым вырезом на расстоянии 1,5 м от

опоры

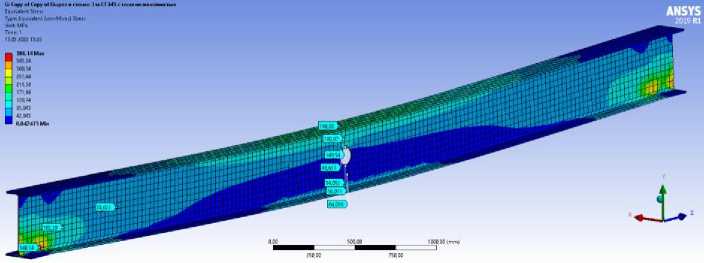
Рис. 10. Эквивалентные напряжения в балке с круглым вырезом на расстоянии 3,0 м от опоры

Выявлено, что почти во всех контрольных точках (кроме точек около круглого выреза) наблюдаются примерно одинаковые значения напряжений. В то же время, в районе выреза напряжения меняются. Например, в верхней точке выреза напряжения составляют 155, 151, 148 МПа соответственно. Поскольку в балках на срез в основном работает стенка, при приближении выреза к опоре логично увеличение напряжений, хотя тоже не очень значительное.

Как и предполагалось в цели работы круглый вырез действительно является концентратором напряжений. При пере- распределении максимальные значения напряжений концентрируются в области дефекта стенки балки. Напряжения в области круглого выреза увеличиваются более чем в два раза относительно того самого участка, но при отсутствии дефекта (увеличение составляет от 75 МПа до 155 МПа).

Выводы. В данной работе было выполнено сравнение напряженно-деформированного состояния шарнирно-опертой двутавровой балки без дефектов и с дефектом стенки в виде круглого выреза, расположенного на разных расстояниях от опоры. Были получены результаты пере- мещений и напряжений в четырех образцах балок, произведен анализ полученных результатов.

Установлено, что в целом наличие круглого выреза не существенно влияет на вертикальные перемещения (прогибы) и напряжения точек вне области выреза.

Также полученные данные подтверждают, что круглый вырез является концентратором напряжений. Значения напряжений в области концентратора увеличивают свое значение более чем в два раза (с 75 МПа до 155 МПа) относительно того же участка, но без выреза.