Напряженно деформированное состояние толстостенной трубы из упругого композиционного в среднем изотропного материала

DOI:

Решение задачи Ляме для толстостенного цилиндра нашло широкое применение в инженерии и строительстве [3]. Кроме того, в настоящее время данная задача находит широкое применение в расчетах и оптимизации конструкций радиационно-тепловых экранов ядерных реакторов, их тепловых и биологических защит и т. д. [1]. Определение напряженного состояния трубы под внутренним давлением является неотъемлемой частью методик анализа дефектности трубопроводной системы [2].

Однако, несмотря на значительный интерес к этой задаче, ее решение для композиционного материала даже в случае упругости его компонент отсутствует. В частности, она может найти применение при расчете НДС труб из керамических материалов.

До настоящей статьи все решения краевых задач для композиционных тел выполнялись с явным использованием гипотезы о малости представительного объема композиционного тела по сравнению с его размерами. В данной статье впервые эта гипотеза отсутствует, вместо этого авторами явно применены гипотезы Фойгта и Рейсса к решению двух отдельных оценочных краевых задач и последующим усреднением полученных величин напряжений и деформаций.

Основные уравнения и гипотезы

Предполагается, что композиционный материал состоит из n компонент, k-я компонента которого (к = 1, n) имеет различные модули упругости Ek и одинаковые коэффициенты Пуассона

n

¹ X ⁿ к =1

ν_k (где ν _k – коэффициенты Пуассона компонент). Относительная объемная n

доля каж-

дого материала у _к ( 0 < у _к <  1 , Х у _к = 1 ). Будем обозначать через R ₁ и R 2 радиусы внутренней и внешней границ сечения цилиндра соответственно (рис. 1). При решении задачи будем использовать результаты для толстостенного цилиндра, изложенные в [3, с. 90–93].

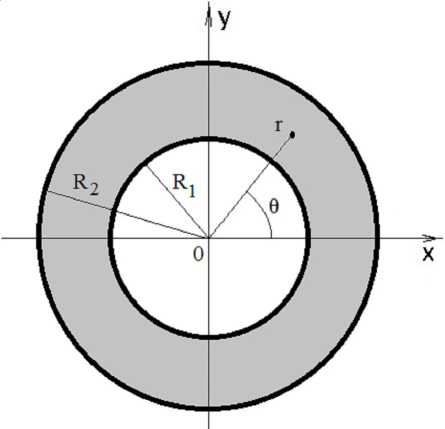
Рис. 1. Толстостенный цилиндр

Гипотеза об однородности деформаций. Плоская деформация

В данном разделе проведем первый этап решения поставленной задачи, заключающийся в использовании гипотезы Фойгта о том, что при простейшем на гр ужении в материале имеет место однородная деформация, то есть для любого k -го слоя ( k = 1, n ) [4, с. 4]:

ε rr , k = ε rr ,   ε θθ , k = ε θθ ,   ε r θ , k = ε r θ .

Кроме того, из независимости решения от угла θ следует, что ε _{r θ} = 0 .

В полярной системе координат в случае плоской осесимметричной деформации уравнение совместности деформаций имеет вид [3, с. 90]:

θθ

-

ε _rr

∂ r

-ε θθ _{= 0,} r

а уравнения состояния определяются обобщенным законом Гука [3, с. 32]:

где σ _{rr , k} , σ_{θθ, k} – нормальные компоненты напряжений k -го слоя ( k = 1, n ).

Непосредственно из (3) можно сразу же получить связь между средними значениями напряжений и деформаций по реализации модулей упругости композита. Поскольку извест но , что относительная объемная доля каждого материала с модулем упругости E_k равна γ _k ( k = 1, n ), то из (3) следует очевидное равенство:

где nnn

( E ) V = ∑ γk ⋅ Ek , σrr > V = ∑γk ⋅σrr,k , σθθ > V =∑γk⋅σθθ,k . k=1                             k=1

Учитывая, что при гипотезе Фойгта ε _rr ≡ ( ε rr _V и ε θθ ≡ ε θθ ) _V , то для решения поставленной оценочной задачи остается расшифровать, что представляют собой σ _rr ) V и ( σ θθ V .

1 ∂ϕk rr V∂

Далее, подставляя (3) в (2), используя выражения σ _{rr k} = ^k , σ_{θθ k} =     ^k , получим уравне-

, r ∂r , ние для определения функции напряжений Эри ϕk k-го концентрического слоя (k = 1,n) [3, с. 90–91]:

∂ ³ ϕ _k 1 ∂ ² ϕ _k 1

3+      2 - 2

∂r3    r ∂r2    r2 ∂r решением которого является функция ϕk = C1,k ln(r) + C2,k r2 + C3,k .

Таким образом, напряжения в k -м слое ( k = 1, n ) примут вид:

σ rr , k

C

=   ¹ ₂ ^{, k} + 2 C 2, k

r

σ θθ , k

C

-   ¹ ₂ ^{, k} + 2 C 2, k .

r

Из (1) и (3) следует, что для любых к и m ( k , m = 1, n ) выполнено:

rr

1 + v

E k

1 + V

^ст rr , к

— VСT66,к ) =

1 + v

^ 66 ~~F~ E_k

Em

1 + V

^СТ rr , m

—

F

Em

^ст 66 , m

— VO" I rr,m .

Решая уравнения (6) относительно ст rr к и Ст бб к , будем иметь:

Ek ст rr, к           ст rr, m ,

E _m

Ek ст66,к =      ст66, m ,

E _m

и с учетом (5) получим соотношения для коэффициентов функции ф к :

Ek             Ek

C 1, к   р C 1, m ,   C 2, к   р C 2, m •

Em          Em

Таким образом, нормальные напряжения на внешней и внутренней границах примут вид:

^C 1,1

^ст rr ,1 r 2

+ 2 E^L C.

E n

э „ ст

2, n ,      rr , n

F. 1

= -nC.    + 2 C

E ₁    1,1   2

r

2, n .

При граничных условиях ст rr 11

I r = R

= ст R

и

^ст rr , n l r = R ₂

= ст R из (9) получим:

R 1² - E n -ст R 1

= E n

- C 1,1 + 2 - R 1² - E 1 - C 2, n

,

Откуда следует

R ₂² - E . -ст„ 2       1 R ₂

= E n - C 1,1 + 2 - R 22 - E 1 - C 2, n .

^C 1,1 = I ^ст R ₁

—

E

—1--ст

E n

R ² J R 2²

R 1² - R 22

—

^R 1^2,

С2 =

2, n

R_x^г - En

1    _{E 1}

2 - ( R

^-ст R 1

—

R ₂ ² - ст

R 2

—

R 1

.

Из (5), (8), (9) и (10) получаем

/

ст„_к = rr , k

V

E к ст к

R 1

E ₁

—

E

—--ст„

E ^{R 2}

n

R 1² - R ₂ ² 1

R 2²

—

R 1²

r ²

+ 2

2 E

R, - — -ст„

1 E     R 1

/

^СТ 66 , к

—

V

E

—- сто

R 1

E ₁

—

E

—--ст„

E R 2

n

R 1² - R

^R 2²

—

2 ^R 1^{2 r 2}

+ 2

—

2 E

R_? —- -ст„

2              R 2

R 1² -

2 - R 12	n - R 2 )
E ^--стК	— R 2 - E
E     R 1 2 - ( R	2 E 2 — R 22 )

,

- -ст_К

R ₂ n

.

Очевидно, поскольку и первым, и по сл едним с лоем могут быть любые материалы со своими модулями упругости E i и E j ( i = 1, n , j = 1, n ), то (11) необходимо переписать в виде:

σ rr,k,i, j

f Ek      Ek     ) R 2 - R ₂ 2 1

Or--- °R --У---

V Ei R   E j   R ² J R 2 - R r 2

2 E k         2 E k

R,   Op — R^   О

1 E    R1     2 E ij

2 • ( Rx — R 2² )

σ θθ , k , i , j

' E L _{О —} E L • _О ) Rx • ^R 22 ± E R E     ^{R 2} I R ₂² — R² r²

V ¹              j У 2        1

+ 2

2 E k

R ¹ ^ E "^{O R} i

i

2 E k

R.       о p

2 E     R 2

j

2 • ( R x² — R 2² )

Далее, домножая на (12) y к ( к = 1, n ) и суммируя по к , получаем:

/о - .\ = E\ rr ,i , j V            V

E

V ¹

R 2 • ^О R _— R 2 • ^{О R 2}

Or ) R ² R ² 1      , _x¹ E ² E

R ₂    R ₁ R ₂     1                          i             j

E j ) R 2² — R x² r² E ^Vv     2 • ( R ₁ ² — R ₂ ² )

σ θθ , i , j

V

2 σ R 1        2 σ R 2

R,Rn fОR Оa r;.r22 1            1 E - Ej

• ■ V I E "X J RRR ⁺ 2'  2-( R ,- — R -)

ij          12

Домножая результат на у_t, суммируя по индексу i , индексу j , окончательно определяем (° rr^V и ^°_ее^ V :

далее домножая на у j и суммируя по

/

где

( ° rr\

° ° ее \

R

V

R

V

.° R 1

—

V

—

( °

R 1

\ ^R ₁ • ^R 2 ^{1       R} 1 ° R ₁ ^R 2 ° R ₂

о n )— 5----5—7 + 2---- f—z----— ,

^R 2' R² _ R²_r²        1- ^R 2 -R 2

^R 2 ^R 1 r             R4 ^R 2 / у

R 1² . R 22 1 , „ ^R 1² .° R 1 ^{— R} 22 .° R 2

• — ° ) + 2

^{R 2} 'r ₂ ² — R ₁ ² r²        2 - R — R ₂ ² )

A у

n

A

—1

R

= yn ^ E X

V A=1

у

Из (4) с учетом (13) для гипотезы Фойгта получаем:

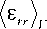
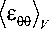
^{( 1} + v ) E_R

^{( 1} + v ) E_R

⁽° R

—

V

—

(°.

, ) R ,² - R 2² 2 R ²' R 2² — R ₁ ² r²

+ 2- ( 1 — 2-v )

^R -^{2 -}° R 1 ^{— R} 22 ^-° R 2 J 2- ( R 1² — R 2² )    ^J

. ) R .² - R 2² 2

^{R 2}' R 2² — R ₁ ² r²

+ 2 ( 1 — 2-v ) -

^R 1^{2 -}° R 1 ^— R 2 ^{2 -}° R 2 2- ( R 1² — R 2² )

\

у

Гипотеза об однородности напряжений. Плоское напряженное состояние

В данном разделе проведем второй этап решения поставленной задачи, заключающийся в использовании гипотезы Рейсса о том, что при простейшем нагружении в м атериале имеет место однородное напряженное состояние, то есть для любого к -го слоя ( к = 1, n ) [4, с. 5]:

orr,k = orr, oee,k =oee, Оre,k = ore .

Кроме того, из независимости решения от угла 0 следует, что о r _g = 0 .

В полярной системе координат в случае плоского осесимметричного напряженного состояния уравнение совместности деформаций в терминах напряжений имеет вид [3, с. 90]:

дoee  v 6° rr дr      дr

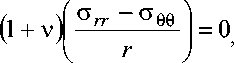
а уравнения состояния определяются обобщенным законом Гука [3, с. 32]:

° rr = ,     2 ^(e rr , k ^{+ Ve} 00 , k ) ,

1 — V

° 00 =       2 ^(e 00 , k ^{+ V S} rr , k ) ,

• 1    — V

где e _rr , k , ^s ee , k - нормальные компоненты деформаций k -го слоя ( k = 1, n ).

Разделив оба уравнения (17) на E k , домножив их на у _k ( k = 1, n ) и суммируя по k из (17), получаем:

n

- 1

n

E _R 1

E _R

•О rr

,    2 ^{( е} rrX ^+V^^S00 r ) ,

1 — V

•° Q0   ₁     2 ^(e "0 r ^+V^^S rr r ) ,

1 — V

где EL = Ej" I , ^e rrk = £ y k -e V k = 1 E k J                 k = 1

Так как при гипотезе Рейсса o rr

n rr,k , ^ee)r = EYk "e00,k .

k = 1

= (o ,^_r и o _ee = (o ₀₀) _r , то для решения второй оценочной зада

чи остается расшифровать, что представляют собой (e _rr^_R и (e₀₀^ _r .

Подставляя в (17) выражения o rr =¹ ^^ , о, r d r функции напряжений Эри ф [3, с. 90-91]:

д ² ф

₆₆ = — y , получим уравнение для определения

⁰⁰ д r²

д 3ф + 1 д 2ф   1 дф = о дr3 r д r 2 r 2 д r решением которого является функция ф(r) = C1 ln(r) + C2 r2 + C3.

Таким образом, напряжения имеют вид:

o rr = C1 + 2 C 2, °00=— C1 + 2 C 2.(20)

rr

При тех же, что и в первой задаче, граничных условиях °Д_R = oR и orr| _r = oR из (20) получим [3, с. 92]:                                                      12

C1 =(o R,—o R 2 ) R12 _R22 ,

^R 2 ^R 1

C = ^R ,2 ^o R 1 ^{— R} 22 ^o R 2

• ²     2 • ( R ,² — 2 R ₂ ² ) .

Из (15) и (17) следует, что для любых к и m ( k , m = 1, n ) выполнено:

^С ее

^С rr

E k	( 8 rr , к		rr , m	+ V8 00 , m ) ,
1 — V2 E k 1 —V2		IV 8 00 , к ) 1 — V 2 + V8 rr , к ) =, m 2 1 — V
	(8 00 , к		^ее , m	+ V8 rr , m )-

Решая уравнения (22) относительно 8 _rrk и е₆₆ к , будем иметь:

8„_к rr , k

= E m 8

E k

rr , m ,

⁸ ее , к

E _m „  ⁸I

E k

ее , m .

Кроме того, из (21) и (22) можно получить:

⁸гг к rr ,

• 1    + VZ

=----- (с„

R 1

E _k

—

^С R 2 )

R 1² • R 2

R 2

—

R 1

r ²

1 — V R 12 C

⁺" E T 'H R

R 1

—

—

^R 2 ^С R 2

• 2    R 2² ) ,

⁸ ее , к =

—

1 + V /

^(С R , E _k

—

^С R 2 )

R 1² • R 2

R 2

—

R 1² r ²

1 — v R 12 C

⁺ E . 'T R

R 1

—

—

" ^R 22 ^С R 2

2 R 2² ) .

Домножив оба уравнения (24) на у _к ( к = 1, n )

и

выражения для деформаций (8 r^ и (8 ₆₆) :

суммируя по k , получаем искомые средние

1 + V

^(с R

—

^С R 2 )

R 1² • R 2

—

R

R 2

—

2 R 1² r ²

+

1 — V

R 12 C

E /T R

R 1

—

—

1 + V

(с

R 1

—

^С R 2 )

R 1² • R 2

R

R 2

—

R ₁ ² r ²

+

1 — V R 1 С

R 1

^R 22 ^С R 2

2 R 22 ) ,

—

^R 22 ^С R 2

(Е^   ⁽ R ,² — ² R 2² ) ^-

Далее с помощью (18) вычисляем (с rr^R

и

<^С R 1

—

^С R 2 )

R" • R 2

R 1

—

R 2

—

^R 1^{2 r 2}

^С R 2 )

R 12 • R 2

R 2

—

^R 1^{2 r 2}

1 — V R ^C R

•  (< 2R22) •

^R1 ^C R 1 ^{— R} 2 ^С R ₂

( R 1² —2 R 2² ) .

—

R₂ ²с„ 2     R ₂

—

Решение краевой задачи для трубы из композиционного материала

Очевидно, необходимо предположить, что искомые средние деформации (8 rr,, ^8 ₆₆) и напряжения (с rr ^, (с₆₆) определяются выражениями:

(⁸ rr ^ = а^⁸ rr^ +⁽ 1^— а)^ ⁸ rr^R ,

а^8ее)V +(1 — аМ8ее)R,

( ^с rr )=^а(^с _гг\ ⁺⁽1^—а)^^с rx ,

(Сее) = а^Сее \ +(1 — аМСее) R, где а (0 < а < 1) - вещественная константа. Определяя среднее интегральное по возможным значениям а, можно получить из (27) простейшее выражение, называемое в теории композиционных материалов приближением Хилла:

(^S rr^ = 2 '(( ^Е rrX + (^е п\ ) , (^е ее) = 2 " (( ^е ее К ⁺(^Б ее) r ) ,                           ⁽²⁸⁾

(° rr ) = 2 '⁽(° rX ⁺ (° rr R ) ) , ° '- ) = 2 • ⁽(° ее 7 ⁺ (° ее ) r ) .

Устремляя R ₂ ^ да при ° _R = 0 , можно перейти к рассмотрению композиционной в среднем изотропной плоскости с отверстием, тогда для нее из (13), (14) и (25), (26) можно получить:

(° „\. = EV^ ■= ,

R 1²                 E V

• 7Г,  (°ее 7 = ^— E^ "° r ,

•

R 1^{2 ,} r ²

•

^R 1²

2 , r

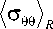
-° R ,

^R 1²

2 . r

^ ° Xr = ° R ,

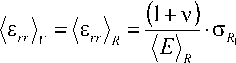
R²   / \    / \      ( 1 + v )

-r T, (See7 =7ее) r =- ,.   '° r ,

•

R 1² r ^{2 .}

Подставляя (29) в (28), получаем, что эффективные деформации по Хиллу в композиционной плоскости с отверстием совпадают со средними по Фойгту и Рейссу, а эффективные напряжения зависят от отношения средних модулей упругости по Фойгту и Рейссу (рис. 2):

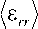
^{( 1} + v ) E_R

•° R ,

•

R

—

^{( 1} + v )

•

r

R

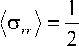
r

^{1 +}

V

V 1

•° R ,

•° R ,

R 1

r 2 ,

•

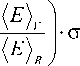
R 1² r ²

.

R 7

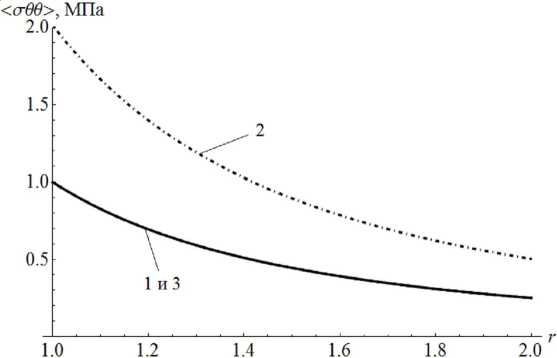
Рис. 2. Непрерывное распределение эффективных напряжений (°_ее^ по (30) в плоскости из композиционного линейноупругого материала с отверстием радиуса R ₁ = 1 м в зависимости от концентраций компонент двухкомпонентного материала с давлением внутри отверстия p = —° _Ri = 10 6 Па с модулями упругости компонент Е , = -10¹⁰ Па , Е ₂ = -10 9 Па при Y , = Y , Y ₂ = 1 — Y : 1 — Y = 0 ; 2 - Y = 1/2 ; 3 - Y = 1

Выводы

Впервые решена краевая задача для твердого композиционного тела без использования нелокальных гипотез о малости объема композиционного материала, для которого устанавливаются эффективные характеристики.

В связи с особенностями постановки задачи в случае композитного материала нет возможности отдельно рассматривать плоское напряженное состояние и плоскую деформацию поперечного сечения трубы, и оба этих состояния будут участвовать в оценке напряженно-деформированного состояния изучаемого объекта согласно стандартным гипотезам Фойгта и Рейсса.