Напряженное состояние системы "кимберлит - вмещающие породы - закладочный массив" трубки "Интернациональная" АК «АЛРОСА»

1. Динамическое проникание твердого тела в грунт

Уравнение динамического проникания твердого тела с осью симметрии в грунт [1, 2] имеет вид du m = Fc,             (1)

dt где m - масса тела; u - скорость; Fc - сила сопротивления прониканию.

Пусть на каждую точку тела, соприкасающуюся с грунтом, действует удельное усилие ac, направленное по нормали, и удельное усилие Т с, направленное по касательной к поверхности в этой точке (рис. 1). Введем две системы координат: фиксированную Ox, связанную с поверхностью грунта, и локальную rO z , связанную с движущимся телом.

Тогда сила сопротивления примет вид

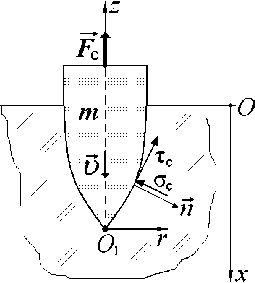
Рис. 1 . Схема удельных усилий сопротивления грунта, фиксированная и локальная системы координат

F_c =— J ( т cos а + a sin a )dS ,    (2)

S где S – площадь поверхности тела, соприкасающаяся с грунтом; tga = f '(z); f(z) - переменный радиус образующей тела.

Выражение (2) преобразуем к виду

x(t)

F_c =- 2 n J ( т _с + a _cf')fdz .       (3)

Отметим, что уравнение (1) с правой частью (3) является практически точным, здесь не было сделано пока никаких предпо-

виде проин-

ложений. Основной проблемой является задание удельных усилий Т_с и а, .

• 2.    Простейшая модель проникания тела в грунт

Максимально простой вариант выражения (3) заключается в следующем: пренебрегаем трением т_с = 0 , а сопротивление грунта прониканию     полагаем     постоянным:

а = const .

Тогда уравнение (1) преобразуется к виду mdU = - Sm (x )а = -nf2 (x )а ’   (4)

dt где Sm - площадь миделевого сечения (поперечного сечения тела на уровне поверхности грунта).

В данном варианте текущая сила сопротивления грунта определяется средним давлением О, и площадью миделя, и она не зависит от формы поверхности тела, уже внедренного в грунт.

Представив ускорение в d" = 1 d и2), уравнение (4) можно dt 2 dx тегрировать:

• ¹    m ( и ² ( x ) - г /² ) = ^{a V} ( x X

x                                     ,

V ( x ) = J S m ( x ) dx 0

где V ( x ) - текущий объем кратера (котлована) (рис.2); и - начальная скорость удара.

Пусть тело достигло глубины L и остановилось: и ( L ) = 0, тогда

• 1    mu₀ ² = W ( L ) = а V ( L ),        (6)

• 3.    Учет динамического сопротивления

где W(L) - работа, совершенная силой сопротивления грунта при образовании кратера (котлована) глубиной L .

Соотношение (6) представляет собой энергетическое равенство начальной кинетической энергии тела работе по образованию кратера. В этом смысле удельная величина сопротивления грунта прониканию О_с является энергией, затраченной на образование единицы объема кратера W / V .

Очевидно, что соотношение (6) дает завышенные значения глубины проникания, так как при оценке сопротивления грунта не учитывались трение и инерционные силы.

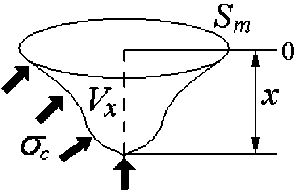
Рис. 2. Схема проникания тела при постоянном сопротивлении грунта без учета трения

Более точный подход к решению задачи проникания твердого тела в грунт должен учитывать трение Т_с и более сложный закон сопротивления σ . Представим удельное сопротивление прониканию в виде суммы собственного (статического) а_о и инерционного (динамического) сопротивления [3]:

а = о0 + kpU,           (7)

где k = sin² а - коэффициент формы; р -плотность грунта.

В этом случае уравнение движения примет вид

1      d                  xx

-^m , U ) = ^{- 2 n} J | Х + ^{( а} 0 ^{+ k} P^U ) f ^{fdz (8)} 2   dx           0

Уравнение (8) интегрируется в конечном виде для тел с простой геометрией, например для конуса или цилиндра с конической головкой. Если рассматривается задача об ударном вытрамбовывании котлована, то трением можно пренебречь, что еще больше упрощает анализ.

• 4.    Задача о забивке сваи в грунт при многократном ударе

Рассмотрим задачу о забивке дизель– молотом длинной сваи в грунт при многократном ударе (рис.3). Задается масса сваи m и молота M, при n-м ударе задается высота падения молота H . В ходе решения требует- ся определить общую глубину погружения сваи хП и погружение ее за один удар Ln.

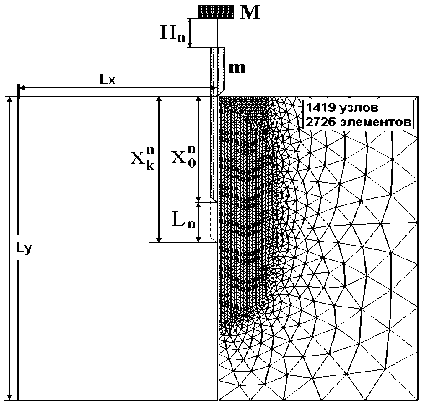
Рис. 3. Схема динамической забивки длинной сваи (параметры – слева) и разностная сетка для расчета процесса проникания численным методом [4, 5] (справа)

Скорость падения молота в момент соприкосновения со сваей без учета сил трения в системе при n -м ударе определяется по высоте его падения:

и n = jh; . (9)

Из закона сохранения импульса (предполагается, что коэффициент восстановления удара равен нулю - неупругий удар) следует начальная скорость внедрения сваи при n-м ударе составляет

„n _ UПМ ^и п

(m + М )

.

Будем полагать удельное усилие трения постоянным, т = const , а головную часть сваи - конической с углом 2 а . Тогда закон движения сваи (8) можно записать в форме линейного неоднородного дифференциального уравнения относительно квадрата скорости:

—(и²) = A + Bx + С и ²,        (11)

dx f П\ в 4nRT с 4-Rip, (12) m + М    m + М    m + М где R - радиус цилиндрической части сваи.

Решение уравнения (11) с начальными условиями и ( х = х П ) = U n имеет вид

° ² = ( A + B + Bx П + U n )>xp( C ( x - x ⁿ n )) —

-

ABB

(— +— x +— x )

C C ²   C

откуда с учетом условия остановки сваи u ( x = x n ) = 0 можно получить соотношение для определения положения сваи xⁿ после n -го удара:

( AC + B + BCx П + Cu )²)exp( C ( x" n - x П )) =

= AC + B + BCx n

Соотношение (14) не позволяет получить конечное выражение для xⁿ , поэтому упростим уравнение (11), учитывая влияние инерционной составляющей сопротивления в среднем,

^— ( u ²) = A + Bx + ¹ C ( U n )².      ⁽¹⁵⁾

dx              2

Уравнение (15) легко интегрируется, что позволяет получить достаточно простое и физически ясное решение для приращения глубины проникания сваи при n -м ударе:

L = xn - xП =

₌ ( m + М )( и П )² (16) 4 n R ( R ( ^ o + - k PU )²) + x T )

При первых ударах для малых значений xⁿ ( x ¹ = 0 ) основное сопротивление оказывает лобовая коническая часть сваи. С ростом глубины проникания основную роль начинает играть сопротивление трения на боковой поверхности сваи, которое для длинных свай может на порядок превышать лобовое сопротивление.

Очевидно, что для одинаковых начальных скоростей сваи u n = const с ростом глубины ее проникания x ! (увеличением количества ударов n ) приращение глубины проникания L при n -м ударе падает по гиперболическому закону.

• 5.    Примеры расчета

Рассмотрим некоторые численные примеры расчета по предлагаемой методике. На рис. 4 (группа кривых 2) показаны зависимости общей осадки сваи от количества ударов для следующих параметров задачи: R = 10 см;

α = 30°; m + M = 30 кН; σ = 0,5 МПа; γ _грунта = 2,0 г/см³.

Там же показаны зависимости осадки сваи за один удар от номера удара (группа кривых 1).

Полученные зависимости качественно хорошо согласуются с результатами расчетов по программному комплексу [4, 5].

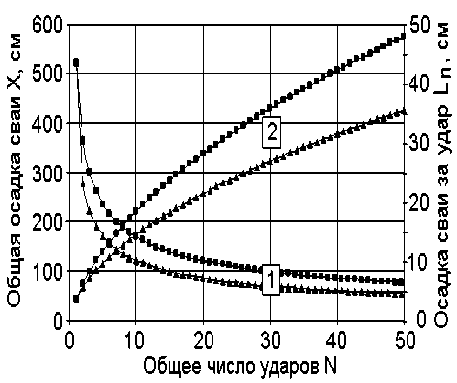
Рис. 4. Зависимость п араметров осадки сваи от количества ударов: τ = 0,05 МПа (квадрат); τ

= 0,1 МПа (треугольник)

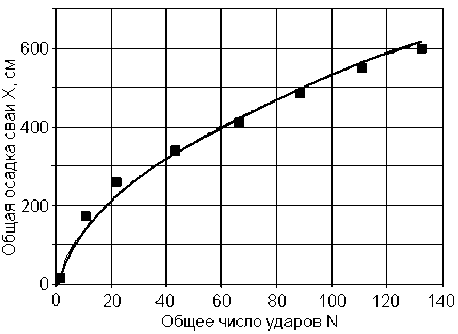
Рис. 5. Зависимость общей осадки сваи от количества ударов: численное решение двухмерной динамической задачи (квадрат); приближенная методика (линия)

Постановка задачи численного моделирования в рамках двумерной нестационарной упругопластической контактной задачи приведена в [4], численная схема реализована в виде пакета прикладных программ PILE GROUND [5].

На рис. 5 показаны сравнительные результаты расчета по предлагаемой прибли- женной методике с результатами численного моделирования, требующего больших вычислительных затрат.

Параметры расчета по приближенной методике: вес сваи 20 кН; вес копра 10 кН; диаметр сваи 40 см; удельный вес грунта 1,8 гс/см³; начальная скорость удара 3 м/с; удельное сопротивление грунта (статическое) σ =

0,17 МПа; удельное трение τ = 0,065 МПа.

Для расчетов по программе PILE GROUND были приняты следующие параметры грунта: сцепление c = 2 кгс/см²; угол внутреннего трения ϕ = 15⁰; коэффициент Пуассона µ = 0,33; начальный объемный модуль K = 59 кгс/см².

• 6.    Заключение

Предложена инженерная методика расчета проникания сваи в грунт при многократном ударе, позволяющая с минимальными затратами оценить влияние основных параметров процесса на динамику ударного погружения.

При глубинах более 3–4 м величина осадки сваи за один удар сильно уменьшается и не превышает 5–10 см. Показано значительное влияние трения на затраты энергии при ударной забивке длинных свай на глубину 5– 10 м, когда количество ударов может достигать нескольких сотен.