Научное обоснование замены макрокинетической задачи микрокинетическим уровнем решения при моделировании процесса сушки дисперсных материалов в псевдоожиженном слое

Псевдоожиженный слой обладает рядом уникальных свойств, обеспечивающих ему многочисленные приложения: высокая теплопроводность, теплоотдача, низкое внутридиффузионное сопротивление при работе с дисперсным материалом, эффективное использование рабочего объема, простота конструкции аппарата, легкость ввода и вывода материала и др. Эти достоинства псевдоожиженного слоя делают его особенно привлекательным для проведения процессов сушки. Сушка в псевдоожиженном слое дает наилучшие результаты в смысле равномерности обезвоживания. При этом практически устраняется комкование и прилипание материала к внутренним частям сушильной камеры.

Объектами процесса сушки являлись хлебопекарные дрожжи, свекловичный жом, а также другое сырье растительного происхождения с развитой поверхностью межфазового влагообмена в процессе обезвоживания. Движение теплоносителя через слой дисперсного материала показано на рис.1 [1].

Принято считать, что в псевдоожиженном слое все частицы находятся в одинаковых гидродинамических условиях. Интенсивное перемешивание частиц гарантирует и одинаковые массообменные условия [2].

1X5

Рис. 1. Общая схема процесса: 1 – теплоноситель; 2 – газораспределительная решетка; 3 – сушильная камера; 4 – ожиженная частица; 5 – отработанный теплоноситель

На основе макроскопического подхода выполнена количественная оценка массообменного условия.

Пусть h - высота псевдоожиженного слоя, S - площадь поперечного (проходного) сечения рабочей камеры. Выделим на высоте x элементарный объем высотой ∂ x и рассмотрим совокупность материальных потоков в нем. Масса влаги (в кг), входящая и выходящая из сечений x и x + ∂ x за время дт , составит:

д m ( x, т ) = u c ( x, т ) S дт ; (1)

д m ( x + д x, т ) = u c ( x + д x, т ) S дт , (2) где u - скорость сушильного агента в слое, м/с; u = const; c ( x , т ) - концентрация влаги в сушильном агенте, кг.

За то же самое время ∂τ в элементарном объеме произойдет съем влаги с дисперсных частиц в размере дm0(x,т) = в\с0(x,т) - c(x,т)]Sдxдт , (3)

где в - коэффициент массоотдачи влаги с поверхности дисперсной фазы в объем сушильного агента, м/с; c ₀( x, т ) - текущее содержание влаги в частицах, находящихся в элементарном объеме.

Тогда изменение массы влаги в элементарном объеме составит дМ (x ,т) = д m (x ,т) -

-д m ( x + д x , т ) + д m ₀ ( x , т ).

На основании (1) - (4) запишем дМ (x ,т) = un( x,т) Sdт - uc (x + д x ,т) х х Sdт + в\ c0( x ,т) - c (x ,т)] S д x дт.

Используя разложение в ряд Тейлора [3] c ( x + д x , т ) в окрестности точки x и одновременно деля правую и левую части (5) на Sдxдт , имея в виду, что по определению

дМ(x,т)/S8 xдт = д c / дт,

получим

—) =__uг c(x ^т ) + _Д co(x. _{r )} - cx- т )]. (₆) ∂τ       ∂ x

Уравнение для изменения концентрации влаги в дисперсных частицах в элементарном объёме [4] примет вид, в предположении об интенсивном перемешивании твёрдой фазы в нём дCо(X,T) = -k [c о (x, т) - c (x, т)],         (7)

∂τ где к - коэффициент сушки, 1/с.

Будем иметь в виду, что в течение процесса c ₀ >>c , поэтому система (6) - (7) может быть существенно упрощенa до квaзинесопряженного видa

=_uд^fcт> + Pcо( x ,т);(8)

∂τ∂

^ =-кс(x,т)(9)

∂τ c очевидными граничными условиями c (x ,0) = п (0, т ) = 0;(10)

йо(О,т) = c^.(11)

Из (9) и (11) следует, что п0(x,т) = c^ exp(-кт) .(12)

На основании (12) задача (8) и (10) зaпишется в виде

8 c ( x , т ) _      8 c ( x , т )

8 т            д x

+ Pc exp( - кт), c (x ,0) = п(0,т ) = 0.(14)

Введём относительные переменные:

X = x / h ; 9 = к т ;

H = u /(kh); C (X, 9) = c (x, т) / c^, и с достаточной степенью точности для инженерных расчётов в « к, тогда задача (13) и (14) в безразмерном виде будет

откуда

A -— 1/ln(1 — 5 ) ,

9 C ( X , 9 )      .9 C ( X , 9 )       .

---= - A ---+ exp( -° ) , (15)

9 9           9 X

C ( X ,0) = C (0, 9 ) = 0 . (16)

Решение (15)-(16) получаем интегральным преобразованием Лапласа по переменной 9 , причём в пространстве изображений получим

~

A dC(,s) + SC~(X, s)Г = 0, dXs

N(0, s) = 0,(18)

где s и N ( X , s ) - изображения 9 и N ( X , s ) . Решение (17) и (18):

~        1

N(X’s) = "7—K[1-exP- , s)L

s( s + 1)

Переходя для (19) к оригиналу, имеем

выражение

N ( X , 9 ) = 1 — exp — 9 ) - 1 -

—

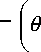
- К1— A Л

exp -

—

( 9 — - ) A

,

которое является решением поставленной задачи, причём 1 (...) есть функция Хевисайда. Из (20) следует, что на выходе из слоя сушильного агента относительная концентрация влаги в нем составит

N (1, A -¹) = 1 — exp — A -¹) .                 (21)

Зададимся приемлемой величиной изменения концентрации 5 (на практике эта величина составляет « 0.1 % ) на выходе, то есть

или в размерном виде

— > 10 ³ . (22) h / и

Условие, что отношение обратной величины коэффициента сушки ко времени пребывания сушильного агента в аппарате с псевдоожиженным слоем должно быть больше 10 ³ , означает правомерность того, что все частицы псевдоожиженного слоя будут находиться в равных массообменных условиях.

Если проводить и теплообменную аналогию, то можно получить такого же приблизительно вида условие, как и (22), в котором вместо коэффициента сушки будет фигурировать, например, приведённый коэффициент теплоотдачи.

Таким образом, обосновано рассмотрение вопроса на уровне отдельной частицы в псевдоожиженном слое, поскольку вся совокупность частиц находится в равных гидро- и тепломассообменных условиях.