Наведение управляемого летательного аппарата по методу трех точек

Баллистика – наука, изучающая движение тел в пространстве под действием различных сил, таких как гравитация, сопротивление воздуха и многое другое. Одним из основных методов, используемых в расчете баллистической траектории ЛА, является метод трех точек. В этом методе тело рассматривается как движущееся между тремя точками: начальной точкой – пунктом управления, промежуточной точкой – летательным аппаратом и конечной точкой – целью [2].

Чтобы рассчитать траекторию тела, необходимо знать начальную скорость, угол наклона начальной скорости, расстояние между точками, ускорение свободного падения и другие параметры. Используя эти данные, можно определить время полета тела, максимальную высоту, на кото- рую оно поднимется, и другие характеристики движения.

Метод трех точек является одним из самых простых и точных методов расчета траектории тела в баллистике. Он широко используется в различных областях, таких как артиллерия, ракетная техника, авиация и космонавтика [1].

Суть метода

Метод трех точек, также известный как «метод совмещения» или «метод накрытия цели» – это способ управления полетом летательного аппарата (ЛА), при котором он постоянно должен находиться на линии, соединяющей точку старта и цель. Это означает, что начальное положение ЛА, его конечное положение (цель) и точка управления (место оператора) должны быть на одной прямой.

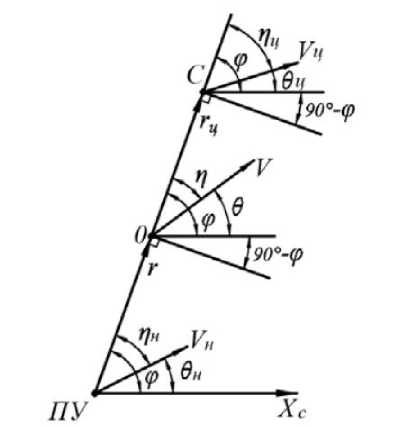
Рис. 1. Схема наведения методом совмещения

В общем случае, положение цели и пункта управления может меняться. Например, при наведении управляемой ракеты “воздух-воздух”. В некоторых случаях пункт управления остается неподвижным, а цель перемещается. Также возможно, что пункт управления движется, а цель остается неподвижной.

Графическое построение кинематической траектории при наведении методом совмещения представлено на рисунке 2 [3].

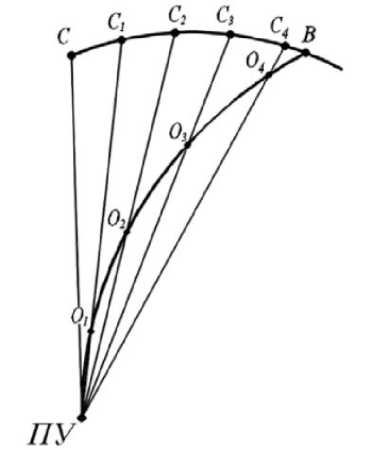
Рис. 2. Кинематическая траектория

Математический расчет

Система дифференциальных уравнений для ЛА:

dV dt

= Vcos6;

dy

— = Vsm6;

R     -^       ^s:^.;

m      2m

d9 dt

Ra mV

c “ aSpV  gcos6

2m       V '

Учитывая, что цель летит равномерно и прямолинейно:

dx _ dt = ^Чц ;

^ = o .

Расчёт времени схода с направляющих t d и скорость схода с направляющих V d :

^Ч д = t" s(^{sin 9} д + Ар cos 0 д ^)]Ч;

А

=1

__________2£н__________

^^- ^-g^(sine g ⁺f mp cose p )

Заданы начальные условия, соответствующие моменту схода ЛА с направляющих:

t = t д ; V = V д ; θ = θ д ; y c = L н · sin θ д ; x c = L н · cos θ д

Заданы начальные условия для цели:

t=t 0 ; V ц = V ц0 ; θ ц = 0 или θ ц = π; y сц = y сц0 ; x сц = x сц0

Расчет активного участка наведения:

При построении кинематической траектории следует соединить прямыми соответствующие положения цели и пункта управления. Центр масс ЛА все время находится на линии «пункт управления–цель»

Динамическую точность будем характеризовать минимальным расстоянием между ЛА и целью в процессе наведения:

^г = ^(^ с ц ^-^ с ⁾² + (У с ц ^-У с ⁾².

Из угловой скорости линии визирования, находим требуемый угол возвышения ЛА:

йф Ч cos (6 + 2 - ф) Ч cos (0ц + 2 — ф) dt            г                     гц

/Ч cos (^ + Ч-

0треб = arccos -------------

-

-•г)-е-’>

Угол атаки – α, с помощью которого можно влиять на угол возвышения находится:

а =

d0 , dt+5

cos 0

Й-

d0

где 77 = dt

⁰ треб ⁰ h .

_R_ c^'

тЙ + 2m

На угол атаки накладывается ограничение:

|а| < адоп, где αдоп = 25° - максимально допустимый угол атаки.

Для определения нормальной перегрузки n y используется соотношение:

/?а +Y

пу =

тд

В начале наведения, когда r/r ц << 1, получаем траекторию наведения, близкую к кривой погони, так как η ≈ 0 и вектор скорости ЛА направлен примерно на цель. В конце наведения, когда r/r ц ≈ 1, получается траектория, близкая к траектории параллельного сближения, поскольку в этом

У случае sin п ~ —"—.

J            Уsmnц

Нормальное ускорение ЛА, наводимого на цель по методу трех точек, зависит:

• -    от величины пути цели до ЛА; чем больше дальность стрельбы, тем меньше

кривизна кинематической траектории; с приближением цели к ЛА потребные нормальные перегрузки ЛА увеличиваются;

• -    от скорости цели; с увеличением скорости цели нормальные кинематические ускорения возрастают во всех случаях стрельбы.

Начальные данные, принятые для расчета, приведены в приложении.

Результат для первого случая (V ц =70, θ = 0) приведен на рисунках 3-6.

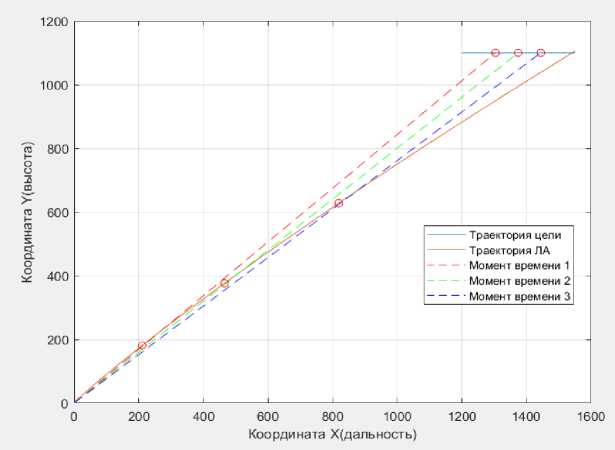
Рис. 3. Зависимость высоты от дальности

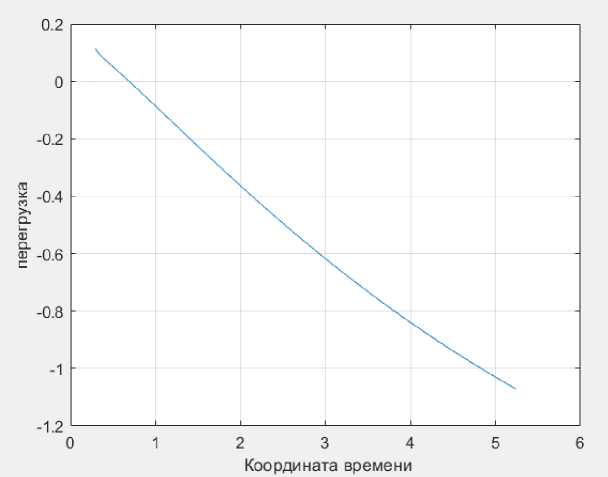
Рис. 4. Зависимость перегрузки от координаты времени

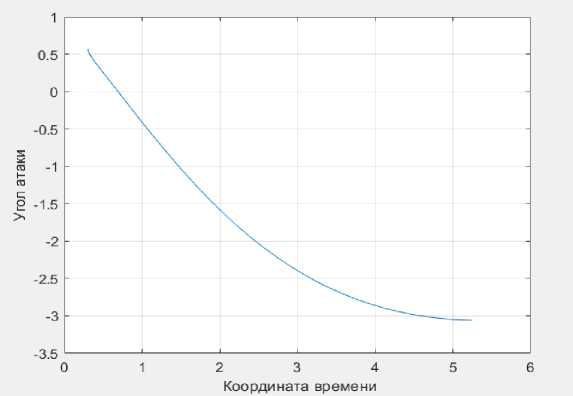
Рис. 5. Зависимость угла атаки от координаты времени

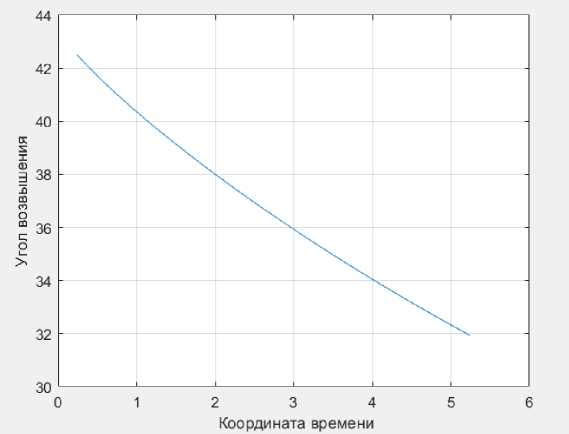
Рис. 6. Зависимость угла возвышения от координаты времени

Результат для второго случая (V ц = 70, θ = π) приведен на рисунках 7-10.

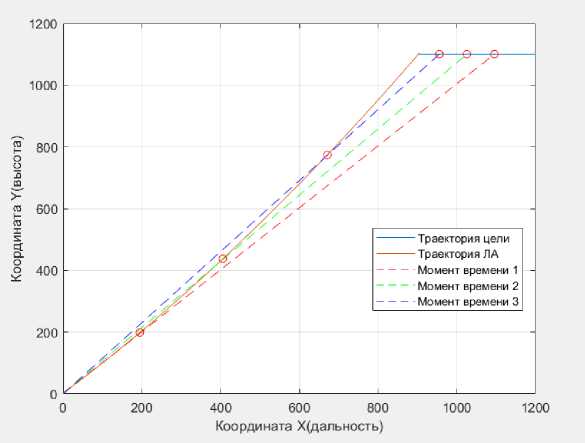
Рис. 7. Зависимость высоты от дальности

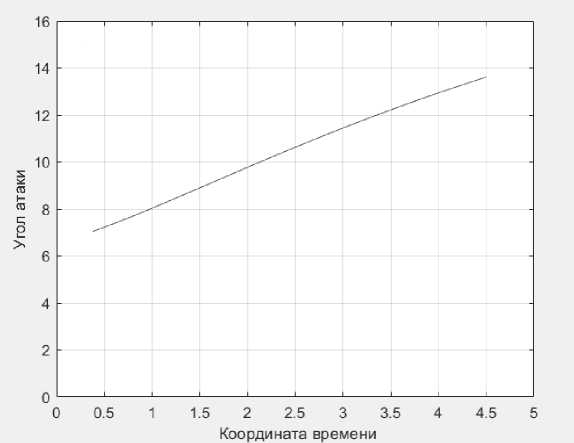
Рис. 8. Зависимость угла атаки от координаты времени

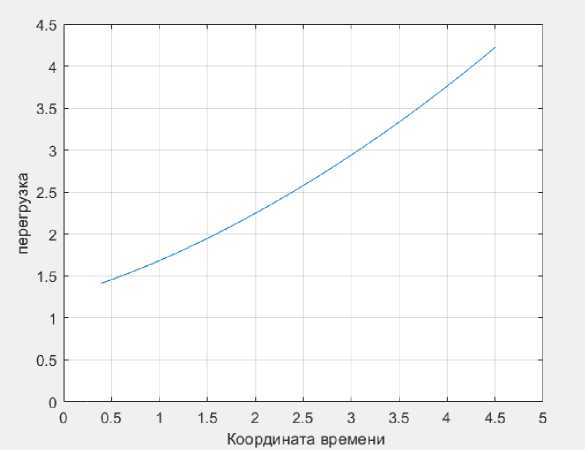
Рис. 9. Зависимость перегрузки от координаты времени

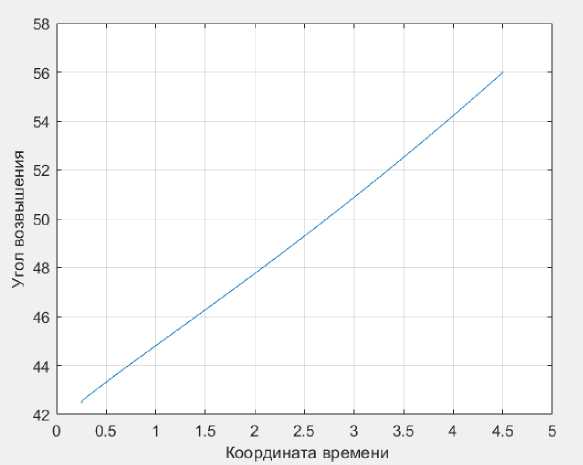
Рис. 10. Зависимость угла возвышения от координаты времени

Вывод

В процессе выполнения данной работы с помощью метода «трёх точек (метода совмещения)» удалось построить траекторию полёта ЛА и цели, с нанесением трёх лини визирования. Для решения дифференциальных уравнений ЛА использовался метод Рунге-Кутты. В ходе моделирования было выявлено, что с увеличением скорости значительно возрастет как промах, так и перегрузки у ЛА. Однако перегрузка так же зависит от угла атаки ЛА и чем он сильнее изменяется, тем больше перегрузка.

ПРИЛОЖЕНИЕ А

Программа в Matlab для решения получения зависимостей угла возвышения, перегрузки, угла атаки от координаты времени и высоты от дальности clc; clear;

g=9.81;

m0=195;

mk=75;

Q=8.5;

S=0.034;

x_aim(1)=1200;

y_aim(1)=1100;

v_aim=70;

teta_aim=0;

h=0.01;

cx=0.3;

A=2;

cy=1;

lnn=3;

uuu=2500;

f=0.15;

R=Q*uuu;

m(1)=m0;

y(1)=lnn*sin(pi/2);

x(1)=lnn*cos(pi/2);

alpha(1)=atan(y_aim(1)/x_aim(1));

tetta(1)=alpha(1);

p(1)=1.23*exp(-y(1)/10000);

t(1)=sqrt(2*lnn/(R/m0-g*(sin(tetta(1))+f*cos(tetta(1)))));

v(1)=R/m0-g*(sin(tetta(1))+f*cos(tetta(1)))*t(1);

rr(1)=sqrt(x_aim(1)-x(1))A2+(y_aim(1)-y(1))A2;

r(1)=sqrt(x(1)A2+y(1)A2);

rc( 1)=sqrt(x_aim(1)A2+y_aim(1)A2);

tetaTreb(1)=acos(v_aim*cos(teta_aim+pi/2-alpha( 1))*r(1)/(v(1)*rc( 1 )))-(pi/2-alpha( 1));

ataka(1)=0;

ataka2 (1)=ataka(1)*57.29;

tetta2(1)=tetta(1)*57.29;

ny(1)=(R*ataka(1)+1/2*cy*ataka(1)*p(1)*v(1)A2*S)/(m(1)*g);

t(2)=t(1)+h;

y_aim(2)=y_aim(1);

x_aim(2)=x_aim(1)+v_aim*h;

xn=x(1);

yn=y(1);

vn=v(1);

tetan=tetta(1);

pp=p(1);

mm=m(1);

aaa=ataka(1);

[delx, dely, delv,delteta] = kuku(xn,yn,vn,tetan,mm,pp,aaa);

x(2)=x(1)+delx;

y(2)=y(1)+dely;

v(2)=v(1)+delv;

m(2)=m(1)-Q*t(2);

p(2)=1.23*exp(-y(2)/10000);

tetta(2)=tetta(1)+delteta;

r(2)=sqrt(x(2)A2+y(2)A2);

rc(2)=sqrt(x_aim(2)A2+y_aim(2)A2);

alpha(2)=atan(y_aim(2)/x_aim(2));

rr(2)=sqrt((x_aim(2)-x(2))A2+(y_aim(2)-y(2))A2);

tetaTreb(2)=acos(v_aim*cos(teta_aim+pi/2-alpha(2))*r(2)/(v(2)*rc(2)))-(pi/2-alpha(2));

ataka(2)=(tetaTreb(2)- tetta(2))/h+(g*cos(tetta(2))/v(2))/(R/(m(2)*v(2))+(cy*S*p(2)*v(2))/(2*m(2)));

if abs(ataka(2))>0.436;

if ataka(2)>0

ataka(2)=0.436;

else ataka(2)=-0.436;

end end ny(2)=(R*ataka(2)+1/2*cy*ataka(2)*p(2)*v(2)A2*S)/ (m(2)*g);

ataka2(2)=ataka(2)*57.29;

tetta2(2)=tetta(2)*57.29;

i=2;

while rr(i)

i=i+1;

t(i)=t(i-1)+h;

y_aim(i)=y_aim(i-1);

x_aim(i)=x_aim(i-1 )+v_aim*h;

xn=x(i-1);

yn=y(i-1);

vn=v(i-1);

tetan=tetta(i-1);

pp=p(i-1);

mm=m(i-1);

aaa=ataka(i-1);

[delx, dely, delv,delteta] = kuku(xn,yn,vn,tetan,mm,pp,aaa);

x(i)=x(i-1)+delx;

y(i)=y(i-1)+dely;

v(i)=v(i-1)+delv;

m(i)=m(1)-Q*t(i);

p(i)=1.23*exp(-y(i)/10000);

tetta(i)=tetta(i-1)+delteta;

r(i)=sqrt(x(i)A2+y(i)A2);

rc(i)=sqrt(x_aim(i)A2+y_aim(i)A2);

alpha(i)=atan(y_aim(i)/x_aim(i));

rr(i)=sqrt((x_aim(i)-x(i))A2+(y_aim(i)-y(i))A2);

tetaTreb(i)=acos(v_aim*cos(teta_aim+pi/2-alpha(i))*r(i)/(v(i)*rc(i)))-(pi/2-alpha(i));

ataka(i)=(tetaTreb(i)- tetta(i))/h+(g*cos(tetta(i))/v(i))/(R/(m(i)*v(i))+(cy*S*p(i)*v(i))/(2*m(i)));

if abs(ataka(i))>0.436;

if ataka(i)>0

ataka(i)=0.436;

else ataka(i)=-0.436;

end end ny(i)=(R*ataka(i)+1/2*cy*ataka(i)*p(i)*v(i)A2*S)/(m(i)*g);

ataka2(i)=ataka(i)*57.29;

tetta2(i)=tetta(i) *57.29;

%fprintf('%d %d %d\n',ataka(i),tetta(i),tetaTreb(i))

end disp(rr(i-1))

k1=(x_aim(150)/y_aim(150));

k2=(x_aim(250)/y_aim(250));

k3=(x_aim(350)/y_aim(350));

yy=1:y_aim(i);

xx=k1*yy;

xx2=k2*yy;

xx3=k3*yy;

figure(1);

plot(x_aim,y_aim,x,y,xx,yy,'r--',xx2,yy,'g--',xx3,yy,'b--',x(150),y(150),'r--o',x(150),y(150),'r--o',x(250),y(250),'r--o',x(350),y(350),'r--o',x_aim(150),y_aim(150),'r-- o',x_aim(250),y_aim(250),'r--o',x_aim(350),y_aim(350),'r--o');

xlabel ('Координата X(дальность)');

ylabel('Координата Y(высота)')

hold on;

grid on;

figure(2);

plot(t,ataka2);

xlabel (' Координата времени');

ylabel('Угол атаки');

hold on;

grid on;

figure(3);

plot(t,tetta2);

xlabel (' Координата времени');

ylabel('Угол возвышения');

hold on;

grid on;

figure(4);

plot(t,ny);

xlabel (' Координата времени');

ylabel('перегрузка');

hold on;

grid on;

function [delx, dely, delv, delteta] = kuku(xn,yn,vn,tetan,mm,pp,aaa);

R=21250;

cx=0.3;

A=2;

cy=1;

g=9.81;

h=0.01;

S=0.034;

xa=xn;

ya=yn;

va=vn;

tetaa=tetan;

ataka=aaa;

xaA=va*cos(tetaa);

yaA=va*sin(tetaa);

vaA=R/mm-(cx+A*ataka^2)*S*pp*va^2/(2*mm)-g*sin(tetaa);

tetaaA=R*ataka/(mm*va)+cy*ataka*S*pp*va/(2*mm)-g*cos(tetaa)/va;

xb = xa + xaA*(h/2);

yb = ya + yaA*(h/2);

vb = va + vaA*(h/2);

tetab = tetaa + tetaaA*(h/2);

xbB=vb*cos(tetab);

ybB=vb*sin(tetab);

vbB=R/mm-(cx+A*ataka^2)*S*pp*vb^2/(2*mm)-g*sin(tetab);

tetabB=R*ataka/(mm*vb)+cy*ataka*S*pp*vb/(2*mm)-g*cos(tetab)/vb;

xc = xa + xbB*(h/2);

yc = ya + ybB*(h/2);

vc = va + vbB*(h/2);

tetac = tetaa + tetabB*(h/2);

xbC=vc*cos(tetac);

ybC=vc*sin(tetac);

vbC=R/mm-(cx+A*ataka^2)*S*pp*vc^2/(2*mm)-g*sin(tetac);

tetabC=R*ataka/(mm*vc)+cy*ataka*S*pp*vc/(2*mm)-g*cos(tetac)/vc;

xd = xa + xbC*h;

yd = ya + ybC*h;

vd = va + vbC*h;

tetad = tetaa + tetabC*h;

xbD=vd*cos(tetad);

ybD=vd*sin(tetad);

vbD=R/mm-(cx+A*ataka^2)*S*pp*vd^2/(2*mm)-g*sin(tetad);

tetabD=R*ataka/(mm*vd)+cy*ataka*S*pp*vd/(2*mm)-g*cos(tetad)/vd;

delx=h/6*(xaA+2*(xbB+xbC)+xbD);

dely=h/6*(yaA+2*(ybB+ybC)+ybD);

delv=h/6*(vaA+2*(vbB+vbC)+vbD);

delteta=h/6*(tetaaA+2*(tetabB+tetabC)+tetabD);

end