Некоторые аспекты прогнозирования бизнес-процессов с использованием методов анализа временных рядов и стандартных программных средств

В связи с тем, что экономические и другие условия с течением времени изменяются, то для устойчивой работы и развития предприятий постоянно существует необходимость прогнозирования этого влияния.

Методов прогнозирования существует большое разнообразие, но все они преследуют одну и ту же цель – предсказание событий, которые произойдут в будущем, чтобы учесть их при разработке планов и стратегии развития. Например, предприятия пищевой, легкой промышленности должны прогнозировать выпуск и реализацию своей продукции; университет интересует - сколько студентов, магистрантов поступят в следующем году.

Существует два общеизвестных подхода к прогнозированию: качественный и количественный. Методы качественного прогнозирования очень важны, когда недоступны количественные данные. Как правило, они носят весьма субъективный характер. Методы количественного прогнозирования позволяют предсказывать на основе данных в прошлом, то есть, опираясь на методы статистики. Эти методы делятся на две категории: анализа временных рядов и методы анализа причинноследственных зависимостей [1].

Методы анализа временных рядов позволяют предсказать значение числовой переменной на основе ее прошлых и настоящих значений.

Методы анализа причинно-следственных зависимостей дают возможность оценить факторы, влияющие на значение прогнозируемой переменной. К ним относятся: методы множественно-регрессионного анализа с запаздывающими переменными, экономическое моделирование, анализ лидирующих индикаторов и других экономических показателей. Рассмотрение этих методов выходит за рамки данной статьи, поэтому основное внимание далее обращено на методы прогнозирования на основе анализа временных рядов.

Объекты и методы исследований

Как известно, временной ряд – это набор числовых данных, полученных в течение последовательных периодов времени.

Постулат, лежащий в основе анализа временных рядов, гласит то, что факторы, влияющие на исследуемый объект в настоящем и прошлом, будут влиять на него и в будущем. То есть, основная цель анализа временных рядов заключается в определении, идентификации и выделении (фильтрации) факторов, имеющих значение для прогнозирования. Для достижения этой цели разработаны математические модели исследования колебаний компонентов, входящих в модель временного ряда. Наиболее распространенной из них является классическая мультипликативная модель, использующая периодические данные – ежегодные, ежеквартальные или ежемесячные [1,2]. Ее основными компонентами являются: циклический, нерегулярный и сезонный компоненты, а также тренд.

Результаты и их обсуждение

Классическая мультипликативная модель временного ряда выражает то, что наблюдаемые значения являются произведением ее основных компонентов, иначе

Y i = Т i × С i ×Х i ,              (1)

где Y i - наблюдаемое значение в i-м периоде времени, например, в i-м году, Т i -значение тренда, С i - значение циклического компонента, Х i - значение случайного (нерегулярного) компонента в этом i-м году.

Если бы присутствовали значения сезонного компонента, то формулу (1) необходимо было бы дополнить соответствующим значением S i , то есть

Y i = Т i × С i ×Х i × S i .         (2)

По определению тренд описывает долговременное возрастание или убывание данных; сезонный компонент – четко выраженные периодические колебания данных, проявляющиеся ежегодно; циклический – повторяющиеся колебания, как правило, имеющие такие фазы, как: пик, спад, дно и подъем (рост). Нерегулярный компонент, в отличие от предыдущих, не является систематическим и отражает случайные колебания данных временного ряда, возникающие после учета систематических эффектов.

Из неоднократных наблюдений автора следует, что основными причинами коле- баний тренда являются: изменение технологий, рыночных цен, происходящих в течение нескольких лет; колебания сезонного компонента, имеющих место в силу изменения социального поведения, погодных условий и т.п. в течение года или меньших периодов; колебания циклического компонента – по причине разнообразных факторов, влияющих на экономическую активность в течение более длительных периодов - от нескольких до десятка лет. Нерегулярные, то есть несистематические компоненты, зависят в основном от случайных колебаний данных, разных непредвиденных событий, например, наводнений, землетрясений, длительность которых относительно непродолжительная. Результаты указанных наблюдений хорошо согласуются с [2].

Для иллюстрации указанной выше мультипликативной модели построим по известному временному ряду, отражающему ежегодные доходы реальной организации, полученные в течение 1992 – 2011 гг. (табл. 1), диаграмму их разброса и найдем линию тренда (рис. 1).

Таблица 1 - Данные временного ряда «Доходы организации»

Воспользуемся стандартными компьютерными средствами, в частности, табличным

Годы Доходы (тыс. тенге) Годы Доходы (тыс. тенге) 1992 581.4 2002 1301.3 1993 581.7 2003 1440.5 1994 590.6 2004 1661.2 1995 620.4 2005 1769.8 1996 700.0 2006 1850.6 1997 781.1 2007 1954.3 1998 891.5 2008 2023.5 1999 993.0 2009 2079.3 2000 1110.5 2010 2145.8 2001 1149,0 2011 2429.6 процессором MS Еxcel.

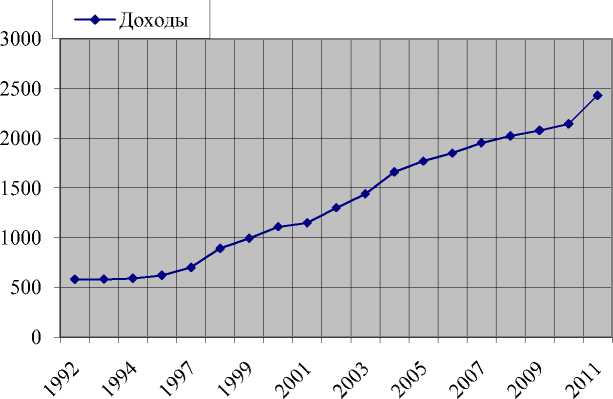
Рисунок 1 - Линия тренда временного ряда доходов.

Из представленной зависимости на рисунке 1 следует, что характерными компонентами для нее являются: циклические (ежегодные), иррегулярные (случайные) и значение тренда. Тренд на указанном графике очевиден, поскольку наблюдается возраста- ние данных, а не их колебания вокруг горизонтальной линии.

Итак, на первом этапе анализа временных рядов построением графика мы выявили зависимость данных от времени и наличие их долговременного возрастания, то есть тренд. В принципе могло бы быть и убывание данных, но и это не меняет возможности применить различные методы прогнозирования на основе ежегодных данных.

Следует заметить, что выше при анализе временного ряда фигурируют фактические данные по доходам рассматриваемой организации, хотя следовало бы их скорректировать, определив реальные доходы с учетом коэффициента изменения потребительских цен за указанный период 19922011 гг. Известно, что величина коэффициента изменения потребительских цен измеряет среднее изменение стоимости фиксированной «корзины» товаров, услуг первой необходимости, предоставляемых городским жителям, т.е. фактические доходы, приведенные в таблице 1, следует умножить на указанный коэффициент. Это необходимо в случае решения конкретной экономической задачи, бизнес-процесса. Но для рассмотрения методологии анализа временных рядов и компьютерных средств принципиального значения не имеет.

Если тренд отсутствует, то можно применить для сглаживания данных метод скользящих средних или экспоненциального сглаживания, позволяющий создать искусственный долговременный тренд [2]. На практике для получения скользящих средних удобно воспользоваться программой MS Еxcel. При этом чтобы сгладить временной ряд, необходимо усреднить исходные данные, а затем построить график временного ряда, используя Мастер диаграмм. Для вычисления скользящих средних применяется простая формула = СРЗнач (указываем диапазон ячеек, содержащих данные по усредняемым годам). Для усреднения удобнее использовать нечетные периоды, например: 3, 5 или 7 лет. Для вычисления экспоненциального сглаживания используется процедура: Сервис

Анализ данных Экспоненциальное сглаживание. Коэффициент сглаживания обычно берется W=0.5 или W=0.25.

Следует особо подчеркнуть, что для кратковременного или долгосрочного прогнозирования среди компонентов временного ряда чаще всего используется тренд [4]. При этом важным является выявление модели тренда, которая в практическом большинстве может быть: линейной, квадратичной или экспоненциальной.

Модель линейного тренда является наиболее простой. Уравнение линейного тренда выражается как:

Ÿi = β o + βi Xi,              (3)

где βi - наклон линии в уравнении линейной регрессии, βo – ее сдвиг; Xi - значения переменных.

Модель квадратичного тренда или, иначе полиноминальная второй степени, является простейшей нелинейной моделью. Уравнение квадратичного тренда имеет вид:

Ÿi i = β o + β 1 Xi + β 2 X i ²,             (4)

где βo - оценка отклика Y 1 , β 1 - оценка линейного эффекта; β 2 - оценка квадратичного эффекта.

Модель экспоненциального тренда выражается как:

Yi=βoβi Xi               (5)

Для того чтобы это выражение свести в линейной регрессии и иметь возможность применить метод наименьших квадратов, следует выполнить над (5) логарифмическое преобразование по основанию 101. Тогда имеем:

Log Yi = log (βoβi Xi) = log βo + log βi Xi = log βo + Xi log βi(6)

Приведя выражение (6) к независимой переменной, получим

Log Ÿi i = βo + β1 Xi ,(6а)

где βo - оценка величины log βo, т.е. 10^βi=ßi, β - оценка величины log β 1 , или 10^β1=ß1

Таким образом, Ÿi = ßoβ1 Xi(6б)

Легко заключить, что (ß 1-1 ) *100% - это ежегодный уровень роста доходов в %.

После вычислений с помощью MS Еxcel уравнения (3), (4), (6) по данным приведенного выше временного ряда имеют вид:

Для линейного тренда Yi = 498,656 + 45,485 Xi(7)

Для квадратичного тренда Ýi = 513,52 + 40,686 Xi + 0,253 Xi2(8)

Для экспоненциального тренда Ÿi = 550,174 * 1,052 Xi(9)

Параметры сдвига в уравнениях (7),(8),(9) составили при условии, что начало координат - 1992 г., а шаг изменения переменных Х равен одному году, соответственно в тыс. тенге: 498,656, 513,52, 550,174 и представляют собой прогнозную величину дохода по отношению к базовому году.

Что касается процедур использования MS Еxcel.

Для построения диаграммы разброса необходимо открыть рабочую книгу (назовем, например, Prognoz.xls); на листе Данные, выбрать команду Вставка → Диаграмма, вызываем Мастер диаграмм и далее щелкнем на корешке вкладки Стандартные, а затем выберем пункт Точечная в раскрывающемся списке Тип; выберем верхнюю (первую) диаграмму с описанием: «Точечная диаграмма позволяет сравнить пары значений», а затем Далее > Диапазон данных, (введите в окне редактирования Диапазон ссылки на соответствующие ячейки). Установите переключатель Ряды в положение В столбцах, щелкните на кнопке Далее >. Заголовки. Введите в окне редактирования Название диаграммы строку Диаграмма разброса, в окнах редактирования Ось Х и Ось Y – соответствующие параметры и единицы измерения. По очереди щелкните на корешках вкладок Оси, Линии сетки, Легенда и Подписи данных. Установите соответственно флажки и переключатели Далее > Поместить диаграмму на листе в положение Отдельном и Готово.

Для применения метода наименьших квадратов исходные данные временного ряда необходимо предварительно обработать [4].

В случае построения линейного тренда для того, чтобы добавить закодированную переменную Х, вставьте в рабочий лист столбец, содержащий целые числа, начиная с нуля. В нашем примере временного ряда цифра 0 соответствует 1992-му году, а 2011- му г. –19. Эти числа лучше всего вставлять с помощью команды Правка > Заполнить > Прогрессия. С этой целью выделим ячейку, например, В1 и выберем команду Вставка > Столбец. В этом пустом столбце запишем в В1 строку Коды, в ячейку В2 запишем 0, выделим ее и выберем команду Правка > Заполнить > Прогрессия. Установим переключатель Расположение в положение По столбцам, а переключатель Тип в Арифметическая. Введем в окно редактирования Шаг число 1, что означает ежегодно, а в окно Предельное значение – 19, завершим ОК.

Чтобы добавить переменную для квадратичного тренда, поступим аналогично, но в рабочий лист добавляем столбец, содержащий формулы, возводящие значения закодированной переменной Х в квадрат. Выделим ячейку, например, С1 и выберем команду Вставка > Столбцы. Запишем в нее строку Квадраты, введем в ячейку С2 формулу « =В2^2 » и скопируем во все нижележащие ячейки вплоть до строки 21.

Чтобы добавить переменную для экспоненциального тренда поступаем также, но в рабочий лист вставим столбец, содер- жащий формулы, вычисляющие значения закодированной переменной Х. Для этого в ячейку С1 запишем строку LOG 10, в ячейку D2 формулу «= Log10(C2)» и также скопируем ее во все нижележащие ячейки до строки 21.

Для вычисления линейного тренда с помощью метода наименьших квадратов над предварительно подготовленными данными выполним команду Сервис > Анализ данных. В этом окне выберем Регрессия >, введем в диалоговом окне Входной интервал Y диапазон ячеек, например, Е1:Е21. затем Входной интервал Х – ячейки В1:В21. Установим флажок Метки, в окне редактирования введем Уровень надежности 95. Установим переключатель Параметры вывода в положение Новый рабочий стол и введем название диаграммы. Далее установим флажок Остатки и График остатков. ОК.

Для построения диаграммы разброса и графика тренда воспользуемся описанной выше процедурой, лишь с той разницей, что в диалоговом окне Линия тренда, щелкнув на корешке вкладки Тип, выберем вариант Линейная, в группе Построение линии тренда (аппроксимация и сглаживание) - Автоматическая.

Вычисление квадратичного тренда выполняется аналогично линейному, но находясь в диалоговом окне, Линия тренда > Тип, выбираем вариант Полиномиальная.

Для вычисления экспоненциального тренда, как и в предыдущем случае, в окне Линия тренда > Тип, выбираем вариант Экспоненциальная.

Построение линии тренда с использованием MS Еxcel показало, что экспоненциальная модель аппроксимирует временной ряд почти также, как и линейная, и квадратичная модели. Скорректированный коэффициент для нее R2 = 0,96, в то время как для линейной модели равен 0,966, а в среднем для всех указанных моделей составляет R2 = 0,96.

Кроме визуальной оценки и сравнения скорректированных коэффициентов R2 в качестве инструмента для определения качества модели можно применить различные способы. Из них заслуживает внимания способ выбора модели на основе вычисления разностей первого, второго порядка, а также относительных разностей. Суть их следующая:

• 1.    Если исходные данные хорошо аппроксимируются линейной моделью, то разность первого порядка должна быть постоянной, т.е. разности между двумя последовательными значениями данных

• 2.    Если исходные данные хорошо аппроксимируются квадратичной моделью, то разность второго порядка должна быть постоянной, т.е. разности между двумя последовательными значениями разностей первого порядка должны быть одинаковыми (Y 3 - Y 2 ) – (Y 2 - Y 1 ) - (Y 4 – Y 3 ) - (Y 3 - Y 2 ) = … = (Y n – Y n-1 ) - (Y n -1 – Y n-2 ).                 (11)

• 3.    Если исходные данные хорошо аппроксимируются экспоненциальной моделью,

должны быть одинаковыми

Y 2 - Y 1 = Y 3 - Y 2 = Y n – Y n -1 .      (10)

то относительная разность должна быть постоянной, т.е. относительные разности между двумя последовательными наблюдениями должны быть одинаковыми

(Y 2 - Y 1 ) / Y 1 * 100% = (Y 3 – Y 2 ) / Y 2 * 100%*= (Y n – Y n -1 ) Y n -1 / 100%. (12)

Вычисленные с использованием MS Еxcel разности первого, второго порядка, а также относительные разности по соотношениям (10) – (12) на основе рассматриваемого временного ряда, поместим в таблицу 2.

Таблица 2 - Разности временного ряда доходов

Годы	Доход	Разность первого порядка	Разность второго порядка	Относительная разность в %
1992	581.4	0.3	8.6	0.000516
1993	581.7	8.9	20.9	0.0153
1994	590.6	29.8	49.8	0.050457
1995	620.4	79.6	1.5	0.128304
1996	700	81.1	29.3	0.115857
1997	781.1	110.4	-8.9	0.141339
1998	891.5	101.5	16	0.113853
1999	993	117.5	-79	0.118328
2000	1110.5	38.5	113.8	0.034669
2001	1149	152.3	-13.1	0.13255
2002	1301.3	139.2	81.5	0.10697
2003	1440.5	220.7	-112.1	0.153211
2004	1661.2	108.6	-27.8	0.065374
2005	1769.8	80.8	22.9	0.045655
2006	1850.6	103.7	-34.5	0.056036
2007	1954.3	69.2	-13.4	0.035409
2008	2023.5	55.8	10.7	0.027576
2009	2079.3	66.5	217.3	0.031982
2010	2145.8	283.8		0.132258

Для наглядности определения аппроксимации временного ряда данных построим графики изменений разностей для рассматриваемых моделей – линейного, квадратичного и экспоненциального тренда (рис. 2). При этом для большей визуализации экспоненциального тренда увеличим масштаб относительных разностей на порядок. Как видим, все указанные тренды: линейный (Ряд1), квадратичный (Ряд2) - удовлетворительно аппроксимируют динамический ряд, но несколько меньшие изменения относительных разностей дает экспоненциальный тренд (Ряд3).

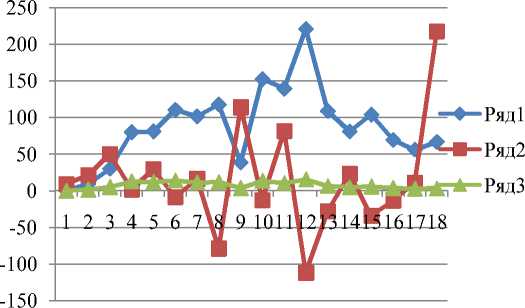
Рисунок 2 - Графики изменения разностей моделей трендов.

Одновременно, из зависимостей разностей для всех моделей следует, что значения временного ряда данных в определенные периоды времени сильно коррелируют как с предыдущими, так и с последующими значениями. При этом следует помнить, что автокорреляция первого порядка оценивает степень зависимости между последовательными значениями временного ряда, второго порядка – оценивает тесноту связи между значениями, разделенными двумя временными интервалами; автокорреляция р-го порядка представляет собой величину корреляции между значениями, разделенными р-времен-ными интервалами. Следовательно, альтернативным способом выбора модели, лучшим образом аппроксимирующим временной ряд данных и дающим возможность более объективно оценить прошлое и получить более точный прогноз, служит авторегрессионная модель [3]. Авторегрессионная модель может быть представлена как:

• - первого порядка

Y i = А 0 + А 1 Y i -1 + b i (13) - второго порядка

Y i = А 0 + А 1 Y i - 1 + А 2 Y i -2 + b i (14) - р-го порядка

Y i =А 0 +А 1 Y i - 1 +А 2 Y i -2 +•••+А р Y i -р +b i (15)

Здесь Y i - наблюдаемое значение временного ряда в i-й момент; Y i - 1 ,Y i -2 , Y i –р -наблюдаемые значения в соответственно (i– 1), (i–2), (i–Р) - моменты времени; А 0 -фиксированный параметр, оцениваемый с помощью метода наименьших квадратов, А1, А 2 ,•••,А р - параметры авторегрессии, вычисленные с помощью метода наименьших квадратов: b i , - случайный компонент с нулевым математическим ожиданием и постоянной дисперсией.

Отметим, что авторегрессионная модель первого порядка напоминает модель простой линейной регрессии; модели второго и р-го порядка - множественной регрессии.

В регрессионных моделях параметры регрессии принято обозначать символами: β0, β 0 , •••, β к , а их оценки - б 0 , б 1 , •••, б к .; в авторегрессионных моделях аналогичные параметры обозначаются символами: А 0 , А 1 , А 2 , •••, А р , а их оценки - а 0 , а 1 , а 2 , •••, ар.

В авторегрессионной модели первого порядка рассматриваются только соседние значения временного ряда; в модели второго порядка – оценивается зависимость и корреляция, как между соседними, так и между последовательными значениями, разделенными двумя временными интервалами; в модели р-го порядка - рассматриваются и оцениваются зависимости и корреляция также, как и для второго порядка, но кроме того еще и между значениями, разделенными тремя, четырьмя и так далее, вплоть до р-временных интервалов.

Выбрав модель авторегрессии и применив метод наименьших квадратов для вычисления регрессионных параметров, следует оценить ее адекватность. Для этого можно использовать либо авторегрессионную модель конкретного порядка, либо сразу построить модель с несколькими параметрами и затем исключить из нее те, которые не несут статистически значимого вклада. В последнем случае оценивается t-критерий значимости параметра Ар, имеющего наивысший порядок, т.е.

t = (а р – А р ) / S ср , (16)

где А р - значение параметра, имеющего наивысший порядок в регрессионной модели, ар - оценка параметра авторегрессии А р , имеющего наивысший порядок; S ср - стандартная ошибка ар.

Для предсказания значений на J лет вперед на основе предыдущих «n» интервалов используем уравнение

Ÿ n+j =a 0 +a 1 Ÿ n+j -1+a 2 Ÿ n+j -2+•••+a р Ÿ n+j -p, (17) где а 0 , а 1 , а 2 , •••, ар параметров А 0 , А 1 , А 2 , •••, А р ; J - номер года в будущем; Ÿ n + j - p -предсказанное значение Y n+ j -p для j -p > 0, Y n+ j – p ; Y n + j – p – наблюдаемое значение Y n + j – p для j -p <= 0

Из выражения (17) ясно, чтобы предсказать значения временного ряда с помощью авторегрессионной модели третьего порядка необходимо использовать лишь последние три наблюдаемых значения Yn, Y n-1 , Y n-2 , а также оценки параметров А 1 , А 2 , А 3 , То есть, для прогнозирования значения временного ряда на три года вперед, уравнение (17) примет вид

Ÿ n+3 = a 0 + a 1 Ÿ n+2 + a 2 Ÿ n+1 + a 3 Y n (18)

Аналогично можно записать значения временного ряда для прогнозирования на 2 года

Ÿ n+2 = a 0 + a 1 Ÿ n+1 + a 2 Y n + a 3 Y n -1 (19) и на год вперед

Ÿ n+1 = a 0 + a 1 Y n + a 2 Y n-1 + a 3 Y n -2 (20)

Заключение

Практика показывает, что использование авторегрессионной модели, хотя и является при прогнозировании весьма непростой и трудоемкой процедурой, но представляет очень полезный инструмент аппроксимации и предсказания значений временного ряда. Для подавляющего числа практических задач прогнозирования оказывается вполне достаточным использование моделей линейного, квадратичного или экспоненциального тренда. Повысить качество аппроксимации, т.е. уменьшить скорректированный показатель R2, дает возможность построение линии тренда с использованием интерполяции полиномом высшего порядка (более чем второй степени). Табличный процессор MS Еxcel позволяет использование полиноминальной аппроксимации до шестой степени.