Некоторые аспекты проведения промежуточной аттестации по дисциплине «Математика» при балльно-рейтинговой системе оценивания

EDN: ZKWFKS

Введение. С 30-х гг. прошлого века в российских вузах используется система оценивания, согласно которой уровень овладения знаниями по дисциплине определяется лишь результатами сдачи студентом экзамена (зачета) в конце семестра. Очевидными недостатками такой системы выступают полная зависимость обучающегося от экзаменующего его преподавателя; невозможность обратной связи и корректировки методов и темпов ведения учебных дисциплин; проблема повторных промежуточных аттестаций. В настоящее время практически во всех российских вузах применяется балльно-рейтинговая система оценивания индивидуальных достижений обучающихся (БРС), сменившая традиционную систему, и имеющая перед ней ряд преимуществ, основное из которых – повышение качества образования за счет регулярной и добросовестной учебной работы студента в течение всего семестра. БРС оценивания состоит из двух составляющих. Первая – накопительный характер оценки, выставляемой студенту по итогам семестра, основную часть которой он получает за текущую учебную работу. Вторая составляющая – рейтинг студента, являющийся интегральным показателем успе- ваемости по всем дисциплинам и характеризующим успешность освоения образовательной программы в целом. В данной работе авторы рассматривают вопросы, касающиеся промежуточной аттестации по дисциплине в семестре. И, хотя в условиях действия БРС на итоговый контроль отводится всего 40 баллов из 100, значение его нельзя недооценивать.

История вопроса. Проблемы контроля качества образования и оценивания знаний студентов вуза по отдельной дисциплине рассматриваются многими российскими и зарубежными исследователями. В частности, М.М. Иванова, В.В. Желонкин и Е.А. Алешин в работе [Иванова М.М., с. 92] поднимают вопрос подбора диагностического инструментария, соответствующего требованиям федеральных государственных образовательных стандартов, анализируют имеющиеся подходы к оценке качества образования, делают попытку подобрать адекватные формы и методы оценивания результатов освоения основной образовательной программы. В работе Н.Н. Мальцевой и В.Е. Пенькова [Мальцева Н.Н., с. 139] анализируются различные подходы к самому понятию БРС, выделятся ее недостатки, предлагаются конкретные меры по совершенствованию БРС для более объективной оценки сформи-рованности компетенций у студентов вузов. М.Ю. Прахова и соавторы [Прахова М.Ю., с. 17] предлагают свою концепции БРС, позволяющую повысить эффективность образовательного процесса и обеспечивающую преимущества как студентам, так и преподавателям и будущим работодателям. Автор работы [Якубчик П.П., с. 29] приводит пример оценки степени освоения студентами отдельной дисциплины, дает оценку эффективности этой системы на практике. Заметим, что указанные авторы основное внимание уделят процессу формирования оценки за текущую работу студента в семестре, лишь вскользь упоминая формирование оценки на экзамене (зачете). Так, Н. М. Меженная [Меженная Н.М.], в целях унификации учебного процесса в рамках модульно-рейтинговой системы, проектирует единые критерии оценивания контрольной работы по дисциплине «Теория вероятностей», анализируя типичные ошибки, допускаемые студентами при решении. Н.Н. Кислова и С.А. Леонов [Кислова Н.Н., Леонов С.А. с. 34] освещают вопросы организации внутренней системы оценки качества образования, указывают ключевые направления, в которых осуществляется контроль качества образования. Ю.В. Гуменникова и соавторы [Гуменникова Ю.В., с. 29], [Гуменникова Ю.В., Золкин А.Л., Богданов М.Р., Узденова М.Б.] подробно рассматривают этапы проектирования и применения накопительной оценочной системы по дисциплине «Математика», в которой баллы за текущую работу не являются обязательной составляющей итоговой оценки, а служат дополнением к баллам, полученным на экзамене. Б.А. Сазонов [Сазонов Б.А., с. 28], анализируя зарубежные БРС, в качестве основной формы итогового контроля по дисциплине рекомендует комплексное тестирование, состоящее из нескольких разделов: общие понятия, основная часть и решение проблемы. Часть ответов студентов проверяется автоматически, по результатам компьютерной обработки, оставшаяся часть -преподавателями соответствующей кафедры, но не теми, что вели дисциплину в семестре. Целью такой ротации является обеспечение анонимности проверяемых работ и, следовательно, объективности оценивания. Вышеуказанный регламент проведения экзамена не всегда можно осуществить в российских вузах, в частности, технических: на выпускающих кафедрах специальную дисциплину может вести единственный преподаватель, которого подчас некем заменить на экзамене.

Материалы исследования. В Приволжском государственном университете путей сообщения (При-вГУПС) студентами технических специальностей дисциплина «Математика» изучается на протяжении четырех семестров, промежуточная аттестация в виде экзамена предусмотрена во втором и четвертом семестрах. Рассмотрим основные принципы формирования экзаменационных билетов для проведения промежуточной аттестации во втором семестре и результаты применения предложенной методики на примере специальности 23.05.06 «Строительство железных дорог, мостов и транспортных тоннелей».

Методы исследования: непосредственное наблюдение, анализ письменных работ и устных ответов обучающихся, анализ количественных и качественных показателей успеваемости.

Результаты исследования. Из ста баллов за освоение отдельной дисциплины в семестре на долю баллов итогового контроля приходится лишь сорок, но недооценивать их значение нельзя - баллы позволяют повысить оценку по дисциплине и значение итогового рейтинга в целом. В мировой практике оценивания студентов основной формой итогового контроля является комплексное тести- рование, однако по ряду причин этот способ не всегда удобен, а в ряде случаев невозможен. Авторы настоящей работы предлагают при разработке экзаменационных билетов придерживаться приведенной ниже схемы.

Первая часть заданий билета оценивается максимум в пять баллов и позволяет проверить знания основных понятий дисциплины. Это могут быть вопросы, требующие короткого письменного ответа. Если брать второй семестр изучения математики в техническом вузе, то в первой части билета мож но предложить следующие определения:

• -    предел последовательности, предел функции при х ^ а и х ^ ~;

• -    непрерывность функции в точке и на интервале;

• -    производная функции;

• -    экстремум функции, точки перегиба графика функции;

• -    первообразная и неопределенный интеграл;

• -    определенный интеграл;

• -    несобственный интеграл и пр.

В основной части билета (двадцать баллов) студенту предлагается для решения несколько типо вых задач по всему пройденному в семестре материалу. Приведем примеры таких заданий:

1. Вычислите предел:

lim x ———1

x — 3 x — 2

x + x

• 2.    Найдите асимптоты графика функции

y = x — 1

и схе-

ма-

тично постройте ее.

• 3.    Вычислите у для функции _у = ^    .

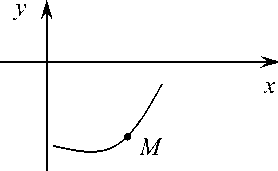
• 4.    Укажите знаки у , у , у в точке М для функции f ( x ) , изображенной на рисунке 1.

• 5.    Вычислите неопределенный интеграл:

  J

  
  

cos 3 x

7 ln³ ( 2 x — 6 ) ( 2 x — б )

dx .

• 6.    Выберите и и dv и укажите du и v для интеграла: J x ⁴ • ln 3 xdx .

• 7.    Найдите площадь заштрихованной фигуры, изображенной на рисунке 2.

  Рис. 1.

  
  
  

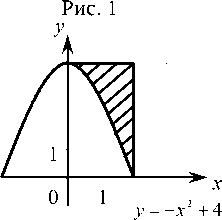
Рис. 2.

Третья часть билета (15 баллов) проверяет готовность студента применить приобретенные знания по дисциплине для решения конкретных проблемных задач, по возможности, связанных с его будущей профессиональной деятельностью. Примеры таких заданий для обучающихся специальности «Подвижной состав железных дорог» приведены Н. А. Архиповой и соавторами в работах [Архипова Н.А., с. 16 а), с. 18 б)]. Для студентов специальности «Строительство железных дорог» можно рекомендовать следующие проблемные задачи:

• 1.    Над центром строительной площадки радиусом 12 м. висит электрическая лампа. Найдите высоту подвешивания этой лампы, обеспечивающую максимальное освещение оборудования, находящегося на краю площадки.

• 2.    Определить размеры прямоугольного сечения балки моста, вырезанной из круглого бревна диаметром d, чтобы её сопротивление на изгиб было наибольшим. Сопротивление балки считать пропорциональным произведению ширины сечения на квадрат его высоты.

Результаты промежуточной аттестации студентов по математике в ПривГУПС во втором семестре 2023-2024 уч. г., проведенной по предложенной методике, показаны в таблице 1. Количество студентов специальности 23.05.06, прошедших промежуточную аттестацию, составило 124 человека.

Таб. 1. Результаты промежуточной аттестации во втором семестре (The results of the intermediate assessment in the second semester)

Количество баллов итогового контроля	От 0 до 10 баллов	От 11 до 20 баллов	От 21 до 30 баллов	От 31 до 40 баллов
Количество студентов (чел.)	29	38	37	20

Рассчитав такие параметры, как качество успеваемости и качество знаний, видим, что абсолютная успеваемость составила 76, 61%; качество знаний – 45,97%; степень обученности – 50%.

Выводы. Применение БРС оценивания индивидуальных достижений студентов приводит к повышению эффективности обучения и качества математических знаний. Проведение промежуточной аттестации по дисциплине является важным этапом ученого процесса, способствующим систематизации и обобщению полученных в семестре знаний. Предложенный вариант семестрового контроля позволяет динамично контролировать качество учебного процесса, способствует объективности оценивания и приобретению обучающимися прочных базовых знаний по математике.