Некоторые свойства аналитического функционального элемента
Автор: Кибирев Владимир Васильевич
Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths
Рубрика: Функциональный анализ и дифференциальные уравнения
Статья в выпуске: 1, 2019 года.
Бесплатный доступ
В данной статье для функций многих комплексных переменных вводится понятие аналитического функционального элемента и аналитичности функции в n- мерной точке. Далее излагаются некоторые свойства теории функции многих комплексных переменных и рассматривается их применение в теории дифференциальных уравнений. Точно так же, как и для функций одного комплексного переменного, применяя интегральную формулу Коши, вводятся различные утверждения и следствия из них. Для доказательства некоторых теорем используются равномерно сходящиеся ряды аналитических функций.
Аналитический функциональный элемент, аналитическая функция, полицилиндрическая область, полицилиндр, интегральная формула коши, сходимость рядов, аналитическое продолжение, модуль аналитического функционального элемента, элементарная окрестность точки, граничное расстояние точки
Короткий адрес: https://sciup.org/148308924
IDR: 148308924 | DOI: 10.18101/2304-5728-2019-1-22-30
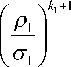
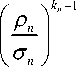
Список литературы Некоторые свойства аналитического функционального элемента
- Владимиров В. С. Методы теории функций многих комплексных переменных. М.: Наука, 1964. 412 с.
- Привалов И. И. Субгармонические функции. М.; Л., 1937. 200 с.
- Фукс Б. А. Введение в теорию аналитических функций многих комплексных переменных. М.: Наука, 1962. 420 с.
- Шабат Б. В. Введение в комплексный анализ. М.: Наука, 1976. Ч. 2. 400 с.
- Янушаускас А. И. Аналитические и гармонические функции многих переменных. Новосибирск: Наука, 1981. 183 с.
