Непрерывная параметризация срединной поверхности эллипсоидальной оболочки и ее геометрические параметры

DOI:

При реализации численных методов [1;4;8;9;11] определения напряженно-деформированного состояния (НДС) оболочечных конструкций различных конфигураций необходимо располагать аналитическими уравнениями срединной поверхности и ее геометрических параметров, определяющих квадратичные формы поверхности [2; 10]. Определение срединной поверхности эллипсоидальной оболочки параметрами декартовой системы координат OXYZ приводит к неопределенности значительного количества точек поверхности на линии пересечения срединной поверхности плоскостью OXZ. При определении НДС оболочек используются криволинейные системы координат с базисными векторами, меняющимися от точки к точке, компонентами в которых определяются векторы перемещений произвольных точек оболочки, производные от которых являются основой для нахождения компонент тензоров деформаций в рассматриваемых точках. В работе получены неортогональные базисные векторы и их производные в этом же базисе для произвольной точки оболочки, расположенной на расстоянии ( от соответствующей точки срединной поверхности. Срединная поверхность представлена радиус-вектором, компоненты которого являются функциями параметров эллиптических кривых, полученных от пересечения поверхности плоскостью OXZ и плоскостями, перпендикулярными оси ОХ. Приведена параметризация срединной поверхности эллипсоидальной оболочки с неопределенностью, возникающей только в одной точке. Определены базисные векторы произвольной точки эллипсоидальной оболочки и получены производные этих векторов в базисе рассматриваемой точки. Эти величины необходимы для использования в прочностных расчетах тонкостенных элементов инженерных сооружений [3;5-7; 12].

а2

№ с2

где а, Ь, с — отрезки, отсекаемые на осях Ox, Оу, Oz.

Координата z срединной поверхности определяется выражением

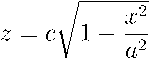
У² №'

из которого видно, что производные координаты z будут иметь области неопределенностей.

При представлении срединной поверхности эллипсоидальной оболочки в декартовой системе координат с ортами % , j , к , векторным уравнением [5; 6]

^ =    + у”] + z к ,

производные радиуса-вектора также будут иметь области неопределенности, поэтому необходимо представлять радиус-вектор поверхности в параметрической форме.

На рисунке 1 представлена срединная поверхность эллипсоида в декартовой системе координат. Эллиптическая кривая в вертикальном сечении xOz (рис. 1) может быть записана в параметрическом виде х = а • sin Т, z = с • cos Т, где Т — параметр, изменяющийся в пределах 0 < Г < 2 (рис. 2).

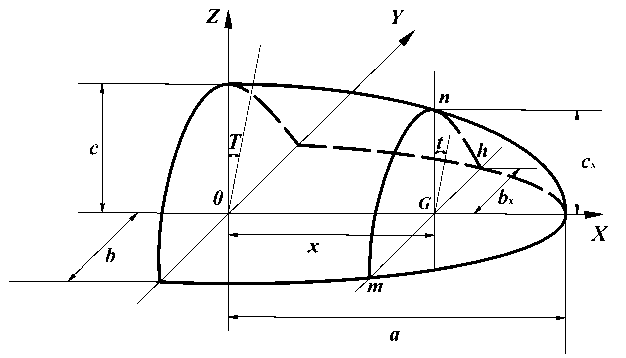
Рис. 1

Координаты эллиптической кривой в сечении эллипсоида плоскостью хОу (рис. 1) определяются параметрическими выражениями х = а • sin Т,

у = b ■ cos Т.

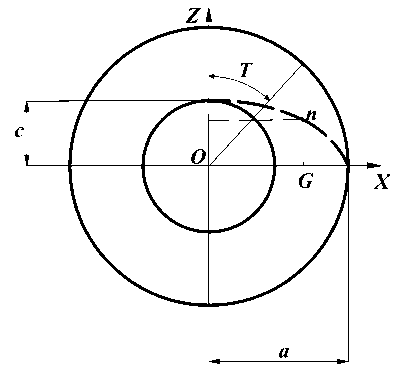
Рис. 2

В сечении срединной поверхности эллипсоида mnh, отстоящем на расстоянии ж от начала координат (рис. 1), с координатами вершин эллипсоидального сечения, определяется на основе (4)-(5) выражениями b_x = b ■ cos Г, с_х = с • cosT, эллиптическую кривую между точками К и Н можно записать в параметрическом виде:

у = b_x sin t,     z = с_х cos t,                              (6)

где параметр t изменяется в пределах — ^ < £ < ^ (рис 3).

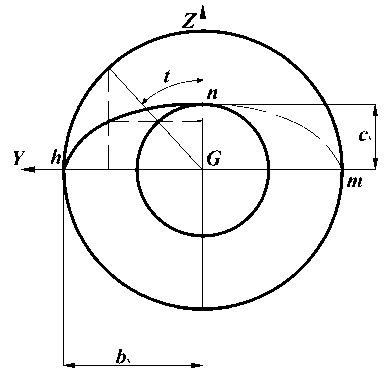
Рис. 3

Используя соотношения (4), (5) и (6), радиус-вектор произвольной точки М срединной поверхности эллипсоида можно записать выражением

^ = а • sin T~i + b • cos Т sin t~3 + с • cos Т cos t к .                 (7)

Векторы, касательные к срединной поверхности эллипсоида в точке М, определяются дифференцированием (7)

о| = Нт = а • cos T~t — b • sin Т sin t~3 — с • sin Т cos t к ;

«2 = R,t = b ■ cos T cos t j — c • cos T sin t к .

Нормаль к срединной поверхности определяется векторным произведением йу X 0>2 |ot х 02,

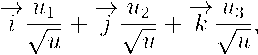
где «1 = Ьс ■ sin Т ■ cos Т ; г/.₂ = ас • sin t ■ cos² Т; u₃ = ab ■ cos t ■ cos² T; u = \/u² + u² + o².

• 1.    Геометрические параметры произвольной точки эллипсоидальной оболочки

Положение произвольной точки эллипсоидальной оболочки, отстоящей на расстоянии £, от срединной поверхности, определяется радиусом-вектором

= 7^ + £,оз.

(Ю)

Векторы локального базиса произвольной точки определяются дифференцированием (10)

7? ^{= rE}t ⁼ R,t + ^з,т — «т + £аз,7;

Тз = R^t — R,t + £^зу = оз + £,оз^;

9з = R^ = 4.(И)

Используя (8), (9), соотношения (11) можно представить в матричном виде

{У} = [т(тлу]{7};   {^} = М"Ч^}-(12)

3x1        3x3    3x1        3x1     3x3 3x1

где{?}^т = {#.92,й;{г} = ССз,кУ

3x13x1

Производные базисных векторов произвольной точки можно представить компонентами в этом же базисе

{ЙУ = У.гН -} = ЫМ-УУ} = М(У};

3x1     3x3 3x1     3x3 3x3 3x1    3x3 3x1

Йй = ыП} = МН-ДУ} = М{У};

3x1    3x3 3x1    3x3 3x3 3x1 3x3 3x1

Ы) = Ы{й} = ЫН^УЙ} = Щ{У};

3x1    3x3 3x1    3x3 3x3 3x1    3x3 3x1

где {7/г}^т — {Тпт, д^т, Уз/г}; Vgff — {71у,771>7зу}; {М}^г — {7nt> 92,tL 77t}; [д,т], 3x1                         3x1                       3x1                         3x3

[т₍], [Ду] ^— матрицы, элементы которых являются производными элементов матрицы [т]

3x3 3x3                                                                                  3x3

по параметрам Т, t, к соответственно.

Как видно из соотношений (7), (8) и (11), неопределенность в значениях геометрических параметров эллипсоидальной оболочки имеет место в точке, определяемой параметром Т = ^. Следовательно, при определении напряженно-деформированного состояния эллипсоидальной оболочки следует исключать часть оболочки в окрестности этой точки.