Нестационарная диффузионная задача для сильно-точных катодов плазмотронов. Постановка и метод решения

Одной из актуальных задач в физике и технике сильноточных плазменных систем (СПС) является проблема повышения ресурса катодных узлов, функционирующих в экстремальных условиях по уровням тепловых потоков и плотностей тока [1]. В последнее время для решения данной проблемы широко используются твердотельные электроды, легированные эмиссионно-активирующими компонентами с малой работой выхода электронов [2]. Однако во время работы из-за высокотемпературной диффузии и интенсивного испарения активаторов снижаются эксплуатационные характеристики катодов данного класса. Исследование динамики этих процессов для оптимизации функциональных режимов СПС представляет собой сложную многопараметрическую задачу.

Постановка задачи

Обобщенная диффузионная задача основана на решении системы из трех нестационарных уравнений в двумерном приближении в цилиндрических координатах с нелинейными граничными условиями: уравнений теплопроводности для всей электродной структуры (катода - тугоплавкой вставки и медного корпуса узла - обоймы), непрерывности тока и диффузии для катода (рис. 1 в [3]). Тепловая задача позволяет определить температурные поля катода T1(r,z) и обоймы T2(r,z) для корректного учета зависимостей коэффициента диффузии D(T) и скорости испарения w(T) при решении уравнения диффузии. Решение тепловой задачи для составного катодного узла представлено в [4].

Двумерное нестационарное уравнение диффузии с учетом нелинейной зависимости коэффициента диффузии от температуры записывается в виде:

^ =¹Д _rD ( t ^ LM d ( t fl 91 r 9r ^v '9r 9 z        d z

D ( T ) = D o exp( - Q^ ).

kT

Граничные условия к (1) поставлены следующим образом:

• а)                      n ( r, z, 0) = n o

• б)                    n ( r, L i , t ) = n ₀ ,       0 <  r <  R i

  в)

  г)

  
  

  D ( t ) ^{8n ( r} A t >  d z

  
  

  ' (1 - n )( n / n м )^2/3w( T ), ( n / n м )^2/3w( T ),

  
  

  0 <  r <  r ₀

  ^r 0 <  ^r <  ^R 1

  
  

  d n (0, z , t ) = 0

  9z         '

  
  

  0 < z <  L 1

  
  

d n ( Rz , t )

д)      - D ( T )    I ¹ ’ >  = ( n / n м )^2/3w( T ),     0 <  z <  L c

9 r dn (R1,z, t) = 0

L c <  z <  L 1 .

9 r          '

Здесь n ( r,z,t ), D ( T) , D ₀, n ₀, Q a - соответственно концентрация, коэффициент диффузии, фактор диффузии, исходная концентрация и энергия активации легирующего элемента (присадки), n _м - концентрация частиц основного металла (матрицы) катода, w( T) - скорость испарения, р -доля атомов присадки, возвратившихся на катод из приэлектродной области в результате ионно-атомного рециклинга [5].

Метод решения

Уравнение диффузии (1) в рассмотренной выше постановке аналитически не решается, так как является квазилинейным уравнением с переменными коэффициентами. Поэтому для численного решения применяем локально-одномерную схему прогонки метода конечных разностей [6]. Чтобы обойти трудности, связанные с выбором системы единиц измерения, а также в целях универсализации решения, исходное уравнение приводим к безразмерному виду:

d y d -5 y 1 d -5 y — = G i — ^{( D} Y) + G 2 ^{( rD} Y), от оz оz r о r о r

D = exp( - QI kT ),

где y = n I n 0,       т = 11 т 0,         z = z IL.,   r = r IR1,

D = DID 0 ,    G = D o T 0 IL 2 ,    G ₂ = D o T 0 I R^ .

Остановимся на некоторых особенностях поставленной задачи. В данном случае использование явных схем нецелесообразно, так как D(T) является быстроменяющейся функцией и условие устойчивости таких схем т < h2 / 2maxD(T) требует очень малого шага т по времени. Поэтому расчет необходимо вести по безусловно устойчивым неявным схемам с ве- сом 8 > 0,5 [7].

Используя пространственно-временную сетку, введенную при решении тепловой задачи [4], с учетом переменности коэффициента D (T), производные уравнения аппроксимируем следующим образом (для уп рощения записи знак «тильда» опускаем):

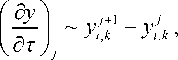
^d _D d y d z d z

~---- h11 L

^{( D} i + 1I2

1A r d r

9y rD dr

~---- h 2IR

^D k + 1I2

y + i ^- y - D y ^- y - 1 )

h11 L1        i-1/2 h11 L1

yk + i ^- yk  _n    yk ^- yk - 1 Y

Di,+ h2IR1      k-ш  h2IR1

^{+      ( D} k - 1I2 "  yk , k ^{+ D} k + 1I2 ' y r , k ),

^{2 r} k

• y_t - y^

где y _k = —--- k-¹- - левая разностная производная в точке yk ;

• ^r , k       h ₂I R₁

• y_{r k} = yk^£+1—yk- - правая разностная производная в точке yk .

• ^r , k       h ₂I R ₁

Коэффициенты D ₍ ik ) _ 1 / 2 = D ( x ,k — 0,5 h 1 , 2 ) , D ₍ ik ) ₊ 1x2 = D ( x ,k + 0,5 h 1 , 2 ) выбираются из условий второго порядка аппроксимации на полушаге пространственной сетки в точках ( x ,_k - 0,5 h ₁ , ₂) и ( x ,_k + 0,5 h ₁ , ₂) соответственно. Это позволяет устранить немонотонность в решении сеточных функций, появляющихся при использовании полных шагов на пространственной сетке. Применяемая схема является абсолютно устойчивой, монотонной, непрерывно дифференцируемой и имеет погрешность аппроксимации 0 ( т + h ² ).

Уравнение (2) в разностном виде запишется:

y{ ^{+ 1} - yJ = G 1 [ D i + 1/2 ( y^ - yJ ^{+ 1}) - D - 1/2 ( yj + — yJ ^{+ 1}) ] / ( h i / L ) +

+ G 2 [ D k + 1/2 ( J - y k ^{+ 1}) - D k - i/2 ( y k ^{+ 1} - y j + i ) ] /( h 2 / R i )² +             (3)

⁺ ~ ^{( D} k - 1/2 ' yr , k ⁺ D k + 1/2 ' yr , k )•

• ^{2 r} k

Применяя локально-одномерную схему, вместо уравнения (3) после- довательно решаем одномерные задачи с соответствующими граничными условиями yj+1 - yJ = G1 [Di+1/2 (y^ - y;+1) - Di-1/2 (yj+1 - yi-11)] /(h1 / L1)2

y k ^{+ 1} - y k = G 2 [ D k + 1/2 ( y k + 1 - y k ^{+ 1}) - D k - 1/2 ( y k ^{+ 1} - y k + 1 ) ] / ( h 2 / R 1 )² +

G

~   ⁽ D k - 1/2 ' y r , k ⁺ D k + 1/2 ' y r , k )

2 rk соответственно по координатам z и r.

Расчет по координате z

После несложных преобразований уравнения (4) имеем:

D i - 1/2 • y i - 1 ¹ - ( D i - 1/2 + D i + 1/2 + 1/ N ² G 1 ) y j ^{+ 1} + D i - 1/2 y. + 1 = y j /( N ² G 1 ) .

Обозначив

Ai = Di-1/2, Bi = Di+1/2, Ci = Di-1/2 + Di+1/2 +1/(N2G1),F = yj /(N2G1), получим разностное уравнение вида:

,h< - C i y i ^{+ 1} + By /' =- F i .

Решение системы алгебраических уравнений такого типа подробно рассмотрено в [4]. Здесь остановимся на деталях аппроксимации граничных условий данной задачи.

После обезразмеривания граничное условие на рабочем торце электрода в разностном виде запишется следующим образом:

• - ^{(1 -} П ^)w 0 L 1 W⁽ N , к ) • y N ^{+ 1} ₀ <  _r <  _r

y N ^{+ 1} - y N - 1 ₌ l     D о n 0 ^/3 n м ^/3 D N - 1/2 ( y N )^1/3 ,           ⁰

^h 2 / ^L 1      I _ ^W0 ^L 1^{W( N} , ^k ) • y N ⁺¹    _r , _r< n

On ^1/3n^2/3O     (v^J Y/³, ⁰      <  ^1.

I D 0 n 0 n м D N - 1/2 ^{( y} N )

Подставив yN1 = aNyN'' + PN в уравнение, находим значение концен- трации yNJ на новом временном слое:

(1 - п ) D N - 1/2 • P n

0 < r < Г), r0 < r < R1,

y^JN + ¹

(1 - « n ) d n - 1/2 + P 1 W( N , k )/( y N )^1/3,

_____________ DN - 1/2 • Pn _____________

(1 - «n ) dn-1/2 + P1W( N, k )/(yN )1/3, где Pi = w0hi/(Dоn01/3nм2/3) - безразмерный параметр; w0 - скорость испарения присадки при температуре Т0.

Расчет по координате r

Подставляя в уравнение (5) выражения соответствующих производных из (3), получим yk+1 - yk = TTGhr [ Dk+i/2( yk+1 — yk+1)—Dk-i/2(yk+1 - yt\) ]+

⁽ h 2 / Ri)

+E D k - i/2 ( У к ^{+ 1} — y k - 1 ) + D k + i/2 ( y k + 1 — y k ^{+ 1}) ] .

2 k ( h ₂ / R _i)

С учетом соотношения M2 = i/(h2/Ri)2 имеем yk+i -yk = G2M2 {Dk+i/2(yk+1 — yk+i) — Dk-i/2(yk+i — j1) +

+E D k - i/2 ( y k ^{+ 1} - j ) +D k + 1/2 ( y k + - y k ^{+ i}) ] } .

2 k

Раскрывая скобки, приведя подобные члены и обозначив

A k = (2 k- 1) D k- 1/2 , B k = (2 k+ 1) D k+ 1/2 ,

C k = (2 k+ i) D k+ 1/2 + (2 k- i) D k— 1/2 + 2 k/ ( G 2 M ²),

F k = 2 ky k / ( G 2 M ²) , M=R 1 /h 2 , получим систему разностных уравнений для значения искомой функции y _k на новом временном слое t = t _{j+ 1}

A    - Ckyf + Bkyk+1 =- Fk ,0 < k < M, где Fk - известная функция, определяемая по значениям функции на предыдущем слое .

На внутренней границе ( k = 0) определяются начальные прогоночные коэффициенты а ₁ и р ₁ .Так как на оси симметрии радиальный поток ра

, ,                 1 д , ^5п.              _ вен нулю, в уравнении диффузии член--(rD —) при r^0 является r д r    д r неопределенностью типа 0/0. Раскрывая эту неопределенность

Id            д 2и lim-—(rD дп) = 2 D ^п r^0 r 5r дr        дr2

на оси симметрии для прогонки по r, получаем следующее разностное уравнение:

y 0 ^{+ 1} - y 0j = 2 G 2 D 0 ₊ 1/2 ( y -+ ¹ - 2 y 0 ^{+ 1} - y /^{+ 1})/( h 2 / R i )².

Поскольку y-jk1 = yj+i, получим y0j+i - y0j= 4M2 G2D0+1/2(yij+i - yk+i).

Сравнивая с y0+i = a1 yJj+1 + в1, находим ai = 4M2G2D0+1/2 /(1 + 4M2G2D0+1/2), в1 = у0 /(i + 4M2G2D0+1/2).

Краевое условие на цилиндрической поверхности в разностном виде запишется как

УМ"’ - УМ-1 _ w0R х w(М, z)yM"’ r _ R h 2/ R,      D0 n 0/3 n     Dm-1/2( УМ )1/3,      ”

^y M - 1 = ^a M ^yM + P m •

Исключая yM11, находим граничное значение искомой функции j+1  ______________DM-1/2 " Pm_______________

D m - 1/2 (1 — « м ) + P 2 w( М , z ) / ( y M )^1/3

с обозначениями

^P 2 = ^W 0 ^h 2 ^{/( D} 0 n 0 n м ), ^D M - 1/2 = ^{( D} M - ^D M - 1 ^)/2.

При прогонке по локально-одномерной схеме разностные уравнения (4) и (5) преобразуем к алгебраической системе вида

Ai,k y(i,k)-1 — Ci,k yi,k+Bi,k y(i,k)-1      Fi,k с условиями Ai,k > 0, Bi,k > 0, Ci,k > Ai,k+Bi,k разрешимости системы данным методом. Далее, решение задачи находим по известной формуле [7]:

У» = a (i,k) y (i,k)+ 1 + в (i,k)+ 1 ,     i = 0,1,2,..., N - 1; k = 0,1,2,..., M -1

_ Ал       R _F,k - Дв

« ⁽ i,k ^{) + 1} = Ck - A a _k ’      ^в i,k ^{) + 1} = Ck - a. «к"

• i ,    k           i , k i , k                                            i , k           i , k i , k

Значения начальных прогоночных коэффициентов a и p i определяются на внутренних граничных условиях катода. Затем из других граничных условий вычисляются значения сеточных функций y N,M и по формуле (6) - все остальные значения y _ik . Переход от времени t к t+ 1 реализуется через последовательное чередование прогонок по координатам z, r . В результате получается двумерное распределение концентрации актива -тора в объеме цилиндрического катода в зависимости от времени работы плазменного устройства.

Математическое моделирование процессов тепломассопереноса проводится в следующей последовательности. Сначала решается тепловая задача в предположении постоянства эмиссионных характеристик катода. Затем, используя поле температур в системе «катод - обойма», решается уравнение диффузии по составленному выше алгоритму.

Заключение

Поставлена и решена в двумерном приближении задача тепломассопе-реноса эмиссионно-активирующих элементов термокатодов цилиндрической геометрии. В совместной постановке решены нелинейные уравнения теплопроводности и протекания тока, диффузии и испарения легирующих компонентов. В задаче строго сформулированы граничные условия, учтены нелинейные зависимости коэффициента диффузии и скорости испарения активатора от температуры. Численный алгоритм позволяет рассчитать поля температур T 1, ₂( r , z ) и концентрации n ( r , z , t ), исследовать динамику выхода активатора из катодов плазменных устройств в широком диапазоне изменения их рабочих параметров.