New mathematical model for the Russian population projections

Бюллетень науки и практики / Bulletin of Science and Practice

UDC 519.248                                        

Population projections are necessary for various administrative areas of state and regional development, for pension policy and public finance planning, for the design and implementation of immigration policies at the national level, for marketing research, and for insurance management. Assumptions about future demographic changes are useful to estimate the future need for food, water, energy, and services, and also to develop social development programs. Besides projections of the future demographic situation has been attracting more attention, thanks to concerns about the possible long-term effects of aging, HIV, AIDS, and COVID.

The actuality of this research is also explained by the fact that the significant changing of the demographic situation in Russia is the result of serious social and economic transformations that have occurred in society over the past several decades. An effective and modern method of research demographic processes and solve global problems of development is mathematical modeling.

In work [1] we represented the analysis of different famous demographic models creating by scientists around the world. As this research showed, in the mathematical demography, deterministic models with discrete and continuous time, and stochastic models with discrete time are more popular [2], [3], [4], [5], [6]. However, as we know, all demographic processes happen in continuous time and are stochastic. The advantage of stochastic models is accounting for the deviation of the frequencies of demographic events from their probabilities. The survey reveals that work with stochastic models is problematic. The main obstacle is difficulties in accounting demographic uncertainty and uncertainty of demographic and economic variables. Thus, the creation of stochastic models and methods of their research methods require development.

In this work, we proposed a new mathematical model for population projections and a new method of research. We considered an autonomous non-Markov queuing system with two types of customers. We indicate the main definition of the process of functioning of this queuing system.

Mathematical model

The autonomous queuing system receives only two types of customers. The customers of the first type are interpreted as a female person and the customers of the second type - as a male person. Their service time is the person’s life expectancy, S i ( x ) and S 2 ( x ) are the survival function for women and men respectively. The process of servicing customers is the following. At first. each customer occupies a free server and is on it for the service time, the duration of which is random. Durations of servicing various customers are stochastically independent, have the same distribution determined by the function S ; ( x ). After completing the service, the customer leaves the system.

For each customer in the system, we define the age x >0. It’s the length of the interval from the time ( t – x ) of the beginning of its service to the current time t . Each first type customer of age x at time t with intensity b ( x,t ) creates a new application. And the probability of this event is b ( x,t )A t + o (A t ), and the probability of generating two or more customers is an infinitely small quantity of a higher order than At. This generating new customer takes a free server and begins the process of its service creating the customers of a new generation. In terms of demography, function b( x , t ) is the birth rate of women of age x in year t (fertility function) and the arrival rate of customers is the process of the birth of children.

We denote as N i ( x i , x 2 , t ) and N 2 ( x i , x 2 , t ) the number of the first and second type customers in the system at time t . Here x is any nonnegative real number. A limits 1

lim —NAx,x + Ax,t) = ^x,t),

Дх->оДх

Нт —N2(x,x + Ax,t) = t](x, t) дх->о Ax will be called the stochastic densities ξ(x,t) and η(x,t) of the number of customers at age x at time t. It’s obvious that

E^x.t) = g(x,t),

Erjtx,^ = m(x,t).

The functions m ( x , t ) and g ( x , t ) define the average characteristics of the stochastic densities ξ( x , t ) and η( x , t ) respectively.

In work [1] we presented a new virtual phase method and a modified method of asymptotic analysis. Using these new methods we solved the problem of investigating the random functions ξ( x , t ) and η( x , t ), and identified their Gaussian distribution with all parameters (first and second moments). But we noticed that the formulas for finding the average characteristics of the random functions ξ( x , t ) and η( x , t ) are similar to Lotka’s model [2] and the component method in continuous time [7], [8]. As shown in our research, such a queuing system sufficiently and adequately simulates the process of changing the age structure of the population and can be used to analyze demographic situations [1]. Now we show the results to the analysis of the population growth in Russia.

Application of the results for the Russian population projection

We take a group of all women and a group of all men of Russia. Our mathematical model is defined by survival functions S i( x ), S 2 ( x ), and b ( x , t ). In terms of demography, these are a female survival function and a fertility function.

We choose the survival functions S i ( x ) and S 2( x ) as a Gompertz-Meikem model [9]. We think that a probability of a girl born is r = 0,488 and a probability of a boy born is ( 1-r ) = 0,512. And we write the function b ( x , t ) in the form

b(x, t) = rj(t№(x, t), where V (t) is the total fertility rate and ^(x,t) is the probability density of distribution for reproductive age of the woman. Focusing on the instability of the demographic process, it is important to select for some other invariant. We found that such an invariant is the distribution of probabilities of reproductive age indicators, which allows the instability of determining the stability of only one parameter — the total fertility rate η(t). We defined that the distribution of the probabilities of reproductive age is invariant from 2000 to 2020, and we can write the function ^(x)=^(x,t) as the density of the bi-parametric Y-distribution

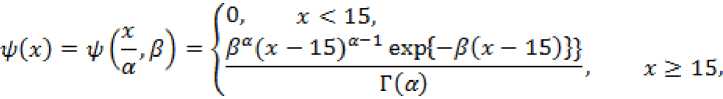
where Г(«) = J™ x^a *e ^Xdx , a > 0. Estimates of parameters a and ft are found using the X ² – method.

We made a forecast of the population in Russia, based on the assumptions about the dynamics of the total fertility rate. The initial conditions are the values of the number of women and men in cc) |

Russia in 2019 according to The Demographic Yearbook of Russia [10]. We assume the total fertility rate ( t ) will be changing from 1,504 to 2,5 in the period from 2020 to 2120. Applying our mathematical model and formulas for the calculation of the average characteristics, we obtain the following values of the average number of populations of Russia by sex in the long run (see figure 1 and figure 2).

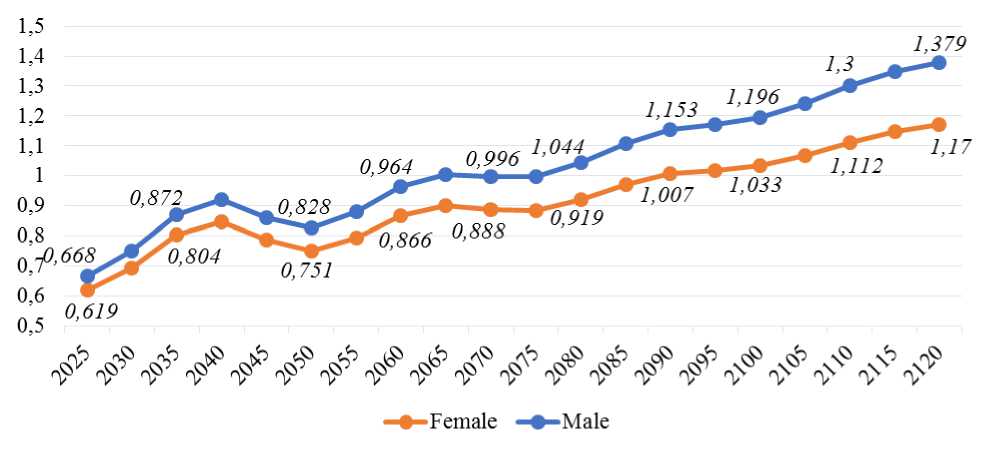
Figure 1. Fertility scenario to 2120 (in millions)

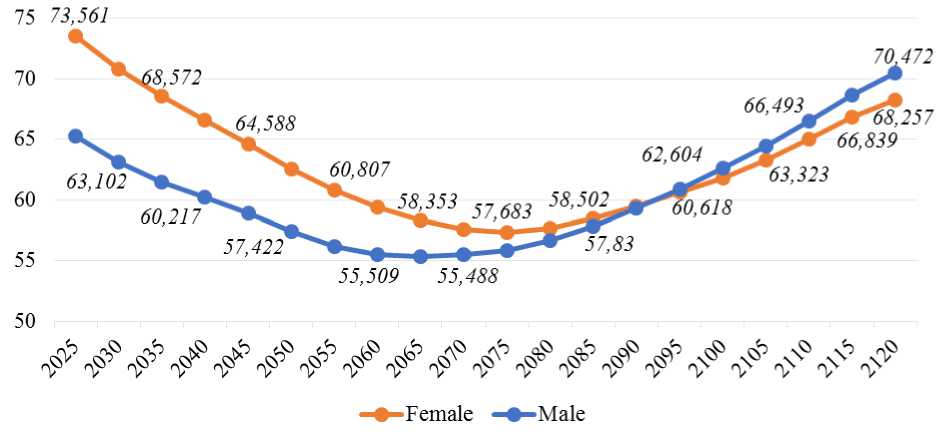
Figure 2. Scenario for Russian population projection to 2120 (in millions)

To check the adequacy of the model and its forecasts, we calculated the values of the age structure of the Russian population for the past years and compared them with real statistics. As the study has shown, there is, of course, a small error in the forecast, but the error is observed only in the last age group and is no more than 5%.

The optimistic scenario assumes that the crisis phenomena in fertility and mortality will largely disappear in a few years, and that demographic development will go smoothly. However, as can be seen from the above results, the optimistic assumption regarding the total fertility rate gives not entirely optimistic results. As can be seen from the graph, the population size in the considered period of time will continue to decline for another 50 years.

A way out of the demographic crisis is possible by the restoration of a stable positive natural population growth or large-scale immigration, which may entail new problems. And the improvement of population reproduction is possible only by ensuring a decent level and quality of life for people.

Therefore the proposed autonomous queuing system with an unlimited number of devices and the developed method of its investigation is an effective tool for estimating long-term population size and for analyzing the demographic situation that has developed.

Conclusion

The article proposes a new stochastic model of demographic growth in the form of an autonomous non-Markov queuing system with two types of customers. In research, we used the virtual phase method and the modified method of asymptotic analysis. We found the main probabilistic characteristics of the number of served customers in the system and was proofed that their asymptotic distribution is Gaussian.

This mathematical model has been applied to the analysis of the population growth in Russia. We have built a scenario for population projections to answer the question of how the Russian population will grow in the period from 2020 to 2120.

The created mathematical model can be modified and can be applied to predict the demographic situation in any country and in the world as a whole, to forecast the population size with considering the age structure, marital structure, and social status, migration processes. The projection of any country’s population plays a significant role in the planning as well as in the decision-making for socioeconomic and demographic development. Mathematical modeling provides an invaluable tool for making assumptions explicit, highlighting key factors determining policy needs, and providing quantitative predictions for the effectiveness and cost-effectiveness of disease control policies.