Non-linear waves in coaxial cylinder shells containing viscous liquid inside with consideration for energy dispersion

Волновые процессы в упругих, вязкоупругих и нелинейных вязкоупругих оболочках, не взаимодействующих с вязкой жидкостью, рассмотрены в работах [1–4], а при взаимодействии оболочки с вязкой жидкостью, но без учета волновых явлений — в [5–7]. Исследование волновых процессов в соосных вязкоупругих оболочках с конструкционным демпфированием при наличии вязкой жидкости, заполняющей пространство между оболочками, отсутствует.

Цель данной работы — получение уравнений, описывающих динамику системы соосных цилиндрических оболочек с учётом вязкой несжимаемой жидкости между оболочками с помощью асимптотических методов, и решение связанной задачи гидроупругости с соответствующими граничными условиями.

Рассмотрим бесконечно длинные соосные упругие цилиндрические оболочки, между которыми находится вязкая несжимаемая жидкость.

В случае осесимметричного течения уравнения движения и уравнения неразрывности вязкой несжимаемой жидкости записываются в цилиндрических координатах r , 9 , x (ось x совпадает с осью симметрии оболочек) в виде [8]:

д V    д V     д V 1 дp   fд2 V 1 д V  д2 VV

—- + Vr—- + Vx—- + —- = vl —^ +--- + —r —r д t      д r      дx p д r    l д r2 r д r дx2 r2

д V д V д V 1 дp   fд2 V   1 д Vд

+ V.+ Vx+     = vl x ++ x д t       д r      дx   p дx    l д r2   r д rд д V V д V

++ д r   rд

На границах с оболочками выполняются условия прилипания жидкости, которые при использовании для описания движения сплошной среды подхода Лагранжа выглядят следующим образом:

V + Um «V_ - W. V -W. , д x         д r        д t

SV      SV SU ⁽¹)

V_x + U⁽ⁱ⁾ —x- - W⁽ⁱ⁾ —x- = £ U_ при r = Ri- W ⁽‘) . д x        д r д t

Здесь: t — время; V_r , V_x — проекции вектора скорости жидкости на оси цилиндрической системы координат; p — давление; p — плотность жидкости; v — кинематический коэффициент вязкости; индекс ( i ) указывает на принадлежность величины внешней ( г = 1) или внутренней ( i = 2) оболочкам; U ⁽ i ) — продольное упругое перемещение оболочки в направлении оси x ; W ^{( 1} ) — прогиб, положительный к центру кривизны оболочки; R 1 — внутренний радиус внешней оболочки; R ₂ — внешний радиус внутренней оболочки ( R 1 = R ₂ +5 ) ; 5 — толщина слоя жидкости в кольцевом поперечном сечении трубы.

Запишем уравнения движения элемента цилиндрической оболочки в перемещениях в предположении, что оболочка деформируется согласно модели Кирхгофа-Лява, а ее материал нелинейно-упругий с кубической зависимостью интенсивности напряжений ст i от интенсивности деформаций e i [9]:

ст i = E ⁽ i ) e i - m ⁽ i ) e ³ , (3)

где E ⁽ i ) — модуль Юнга, m ⁽ i ) — константа материала, определяемая из опытов на растяжение или сжатие.

Кроме этого учтем конструкционное демпфирование материала оболочек, характеризуемое величиной, пропорциональной д W⁽ i )/д t , добавляемой к даламберовой силе инерции [10]

₍ i ) P 0 i ) h 0 i )           E ( i ) д W ^{( i )}

^e g   ^R ( i )  ^ (1 ...   )   ^д t

Здесь e g ) — коэффициент демпфирования; p 0) — плотность материала оболочки; p 0 i ) — коэффициент Пуассона; R ⁽‘) — радиус срединной поверхности оболочки; h 0i ) — толщина оболочки ( h 01) /2 = R ⁽¹⁾ - R 1 , h 0²⁾/ 2 = R ₂ - R ⁽²⁾ ); c 0 i ) = ^ E ⁽ i)J ^p 0 i ⁾ ( 1 - o 0 i ⁾² ) ] — скорость звука в материале оболочки.

С учетом (3), (4) уравнения для описания динамики геометрически нелинейных оболочек записываются в виде [9, 10]:

2           ..х^П2

дU(i)    1 ( дU(i))    (дW(i))      h*i)2 (д2W(i))

---+ - --- + ---- + -⁰— -- ^ -Оо i )^т д x    2 | д x J | д x J 24 | д x ² J ⁰ R ⁽ i )

3x(3))

-

q ( i ) x

f д U ⁽ i ))    _A x д U ⁽ i ) W ⁽ i ) f д U ⁽ i )    W ⁽ i ) )       f W ⁽ i ) Г               д ² U ⁽ i )

l I -(1 + О0 H--^rl ---Mi)l I ^-p°i)h0i l дx  J v ’  дx  R() l дx    R() J ( R() J               д t

E (i) h 0 ' )	/ h 0 ' )2 д 2	[д ‘	W (i)	" д U(i ) )" 1 + д x J	ц * ' ) [ д U ( i )     1 - -^-0- <-----+ — R ( ' ) I  д x     2
1 -ц 0)2	\ 12 д x2		3x 2
	4 m (i) h 0 ' )	1	и (')	2д иV) ? /	( i )A д UW (i) 1 +ц0 ) я nd) ' д x R ( )
	31 -p 0 i )2 R (i)		r	, д x J (

E⁽* )

₊о (**) ^{д 2} W⁽' ) _+е< *) ^р" h 0 ^{+Р о} h ⁰     д t ²        g    R ( ' )

д x

д x

д U ⁽*⁾

д U ⁽ⁱ⁾

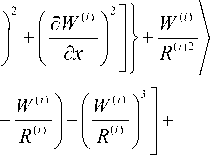
д W ⁽ⁱ⁾

р0' ’ (1 ц'2)    аI

= qn (-1)'

где q x' ⁾ , q n — напряжения, действующие на оболочку со стороны находящейся между оболочками жидкости, приложенные к невозмущенной поверхности оболочки ( W ⁽ ' ) « R ⁽ ' ) ), которые определяются формулами

q

( ' ) = x

pv

( д V д V ) x I r

( д r   дx J

r = r (i)

q

. д V-P+2Pv дr J r = R(i)

.

Принимая за характерный линейный размер длину волны 1 и считая, что соосные оболочки изготовлены из одного и того же материала (что позволяет опустить индекс ( i ) у величин E , m , р ₀, ц ₀, е g ), перейдем в уравнениях (5) к безразмерным переменным:

W ( ' ) = wmu 3 ' ) ,      U ( i ) = u m u^,

C            X *     c 0           * x t = . t , x = . ,      c 0 =      /     2 V                  (7) l               1            \P 0 ( 1 -ц 0 )

Положим

И                w I -m- = е = о (1),   —m— = O (1), 1                   UmR( ) h(i) h- = O (е3/2),   е8= O (е3/2), lg R(i)                 h)n               w — = O (е1/2),   -0-y = O (е),    -m = O (е1/2), 1                  R( )               -m                            (8) E = O (е),   -m = O (е3/2),   -m- = O (е), m                1                   R(i) где е « 1 — малый параметр задачи, заданный с точностью о(1).

Применим метод асимптотических разложений, вводя независимые переменные £ и т в виде

Г       *     _ V*

с,= x - Ct ,

т = е t ,

где c — безразмерная неизвестная скорость волны, т — внутренняя переменная; зависимые переменные представим в виде разложения по малому параметру е :

11 ⁽ ' ) — 11)‘ ) 4- Р/7⁽ ' ) 4-             11)‘ ) — И)'‘ ) 4- Р/7⁽ ' ) 4-                                                       П 0^

— 1       — 10 । е — 11 । ’’’,        u 3       u 30 । е u 31 । ... .                                                  (^ '■')

Подставляя (7)-(9) в уравнения (5), в нулевом приближении разложения по е получим систему линейных уравнений, из которой следует wml umR (‘)

⁽ ' ) и ( о⁾=цо— 30 I 0 д^

и определяется безразмерная скорость волны c2 = 1-Ц2.

Из следующего приближения асимптотического разложения с учетом (11) и (12) находится система уравнений:

²// i ^{)                  2} i ) Я²// i ⁾         /?⁽ i ⁾     Ц²л/1-  ² 4⁴1J) i ⁾

^д u 10  , u m У ^{1 Ц} 0 ^{д u} 10 ^{д u} 10  , ¹ R __    ^У^{1  Ц} 0 ^{д u} 10

д^дт l s 2 д- дХ s( l j 2 д- ⁴

—

11 1      [ sumP0h0°c0 2^ /1-М 2 1 Ц0 L qx

Ц

R ^ д q,

l д^

( —Г¹

2 2 m I u m ] Л	1 U     2)     ц2 P u ‘0'	] 2 д 2 u *0)	R (i)	2 Цо	д 3 u (0)
E s ( l J (	1 ^ 0 + ^ 0 ) y1 ^ 0 1 ( д^	j д^ 2	s g l s	2	д^ 3

При отсутствии жидкости правая часть уравнений (13) равняется нулю, и система распадается на два одинаковых уравнения, представляющих модифицированные уравнения Кортевега-де Вриза-Бюргерса для ^д u ⁽0) М = ^wmm^u 30) /( ^ 0 u m ^{R( i )} ) .

Для определения правой части уравнения (13) введем безразмерные переменные и параметры

V r =       l V r ,

V =    = o (H,

R 2

V = w — v , x m о x , 5

r — R ₂

X = wk = wkRk = O f±) , 5    R ₂ 5    (vj

. C 0           с,            ^pv c 0 lw m p.

t t, x x, p.

l                l5

5 5 R    R .        .. .

— =--- = v — « 1, v « 1, X « 1.

l    R 2 ll

Подставляя (14) в уравнения гидродинамики (1) и граничные условия (2), представим безразмерные скорости и давление в виде разложений по малому параметру X (здесь и далее верхний индекс указывает на номер приближения):

v_x = Vx + X v + ..., v_r = v_r + X v + ..., P = P + X P + ....

xx x     rr r

В нулевом приближении по v величина 5/l® 0 (см. (14)). Тогда, считая (5/l)(5с0/v) « 1, имеем ползущие течения [11, 12]), и в качестве нулевого приближения по X получим уравнения гидродинамики, совпадающие с классическими уравнениями гидродинамической теории смазки дp 0   п дp 0   д2 v0      дvr1   дv0,

---= 0,   ---= —X-,   —- + —x = 0 д r          дx    д r       д rд и граничные условия

° д u ° Л         * 1        °     д u      0 Л* Л vr =—     , vx = 0 при r = 1,    vr =— -ТТ-, vx = 0 при r = 0(17)

д t                                         д t

Из решения задачи (16), (17) следует:

р ” = 12f [ff^ui!!—^uxl) dx 1 dx, J LJ ( дt*     дt* J avx.

^{д r} J r =1

?vx 1 д r   .

-I r =0

.*

Ч¥ I dx* .

Учитывая переменные (9), (10) и найденные величины (11) и (12), из (18) получим

⁰—²   /З/¹)    1/²⁾²   u m Т?*¹)»*¹)    Т?(²)и(²)

^р = ¹²У¹   Ц 0 J ( u 30   u 30 ) d S = ¹² ^ 0\¹ ^ 0 w l ( ^{R u}10   ^{R u}10 ) .                    ⁽¹⁹⁾

Далее, с принятой для s, v, X точностью из (6) найдем напряжения, действующие на оболочки со стороны жидкости ql =

wc₍, д v ⁰

pv "У"

0   д r      „

-I r =1,0

, q n =-pv w m c^ l-P ⁰ ( i = 1,2), 5 5

и следовательно, выражение в правой части уравнения (13) преобразуется к виду:

( - 1) ' 6 _Ц 0

pl    v | 1 + R(i)| p0h0° 5cД 2     5 J

" R ⁽¹⁾ д и/" R ⁽²⁾ д u ₁₀ ⁽²⁾ " ""5   д!    ""5   д!

Учитывая, что 1/2 ^ ц0R(1) /5 (так как ц0R(i) /5 = O(y 1)» 1), можно отбросить первое слагаемое в круглых скобках. С принятой точностью по у, б положим R(1) ® R(2) = R, h01 ® h01 = h0. Подставляя (20) в уравнение (13), окончательно получим д2u(0) + um л]1 о 2 дu(0) д2u(0) + £f R '" ц0У1 -Ц2 д4и0‘0' д!дт +7Б 2 ди д!2 +Б(-J     2     д!4""

-

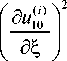
д ² и )

D II² Я³*/ i )                 Л 1        £>У         М  Л      Ди⁽¹⁾   Ди⁽²⁾

^-б g

^R ° 0 ^д u 10  , / .у-1r,,   I ¹ , ^R I ^p l    ^v  I ^R || ^{д u} 10     ^{д u} 10 I _ n

+ ( - 1) 6 Ua + Ua                                      = 0

l б 2 д! ^{3           0} 1 2    ⁰ 5jp ₀ h ₀ 5 c ДбДд! д! J

При отсутствии жидкости (p = 0) последнее слагаемое выпадает, и система уравнений превращается в независимые модифицированные уравнения Кортевега-де Вриза-Бюргерса для дu1(0) /д!, имеющие точное частное решение. Замены д и (1)

—1 = c 311),   П = С1!,   t = c 2 т, д!

где c 1 , c ₂, c ₃ — постоянные коэффициенты, позволяют записать систему уравнений (21) в виде:

дф ^{( 1} )        _w дф ^{( 1} ) д ³ ф ^{( 1} )         ,     ,2 дф ^{( 11}

—— + 6 ф ^{( 1} ) —— + ^-т-- 6g. ( ф ( 1 )) —-- G,

St          др    др^{3      1V} ’ др ²

д ² ф ^{( 1 )} др ²

+ ( - 1) ^{1 - 1} ( ф ⁽¹⁾

-ф ⁽²⁾ ) = 0.

Постоянные c1, c2, c3 определяются из уравнения (21) при подстановке в него (22) и имеют вид r f 1 R Ipl   v f R I c2 = 6p0l-+Ц0-        ---l-l, c1

< 2      5Jp ₀ h ₀ 5 c ₀ б^5 J

1 1 1^^

^ ^{R J} 0 071 -^ 0

c^     2 l б c3 = 6— /—=—. При этом использованы c1 V1 -u2 um

обозначения:

2 c 3 ^c 1 _ r

' 0           6g1, c 2

^Б g

R 0 0 c 2 l б 2 c ₂

Если не учитывать рассеяние

энергии в оболочках, то есть положить б g = 0 ( g ₂ = 0), получим уравнения

«фИ + 6ф" ) ^ф-! -дЛ_ - 6а,(ф - ' ))² дф^- + ( - 1) - -1 (ф™-ф '2)) = 0 ^ = 1,2).            (24)

д t         дп    дп ^{3       Ц 7} дп          ^{v 7}

Проблемы распространения волн в вязкоупругих и нелинейно вязкоупругих тонкостенных конструкциях, в том числе цилиндрических оболочках, без взаимодействия с вязкой несжимаемой жидкостью рассматривались ранее с позиции теории солитонов [13, 14]. Наличие жидкости потребовало разработки новой математической модели и проведения компьютерного моделирования процессов, происходящих в исследуемой системе.

Для оболочек, подчиняющихся гипотезе Кирхгофа-Лява, и при условии осевой симметрии задачи имеем следующие связи между компонентами деформаций бx, бy, соответственно, в продольном и окружном направлении по отношению к срединной поверхности цилиндрической оболочки, прогибами и перемещениями в продольном направлении [9, 10]:

д U ⁽¹⁾ д ² W ^(п 1 ( д U ⁽¹⁾ д ² W ⁽ⁱ⁾ Y 1 ( д W ⁽¹⁾ Y _{( 1 )} --z 1 +—I-- z 1— I +I I , s y

- R r W"   ( ¹ = I.²).

д x      д x ²     2 ( д x      д x ² )   2 ( д x )

где R ⁽¹) — радиус срединой поверхности соответствующей оболочки, z — текущее расстояние от нее. Зададим зависимости компонент напряжений ст _x , ст y и деформаций в виде уравнений квадратичной теории вязкоупругости [15], полагающей линейную упругость объёмных деформаций:

E f-( i )     -( i )]      E        л"₽( t -^T)fl гД^ )W i ’-Ут

^(s x +P o S y J "?— ^a.L e     I ^{1 +} a ^(s u ) ) e x d ^T ,

¹ ^ o                      ¹ ' ^ 0                 ^x

E _;( ^s y ) +0 o ^s x^{1 )} ) ^-T E -^aJ t e ^P t -^f^{1 +} a ^s ( ^s U¹ ) ) ²) e y ) ^{d T} . 1 -p 0 y               1 ■ p ^J- "                          ’ y

Здесь: E — модуль Юнга; ц0 — коэффициент Пуассона материала оболочек (считаем материалы одинаковыми); t — время; а, P, a — вязкоупругие параметры материала; s2 — квадрат интенсивности деформаций; ex , ey — компоненты девиатора деформаций

⁽И^{2      4}((_с⁽ ) \2      с⁽ )       с⁽     )           )     ² с⁽ )    ¹ г⁽ )          )     ² с⁽ )    ¹ г⁽ )

( ^s и ) =3 ( ( ^s x ) ⁺ ( ^s e ) ^-s x ^s y )    e x =J ^s x "  3 ^s y ,    e y =J ^s y "  ^ ^S x .              ( ^2/ )

Разлагая функции

( 1 ⁺ a ( ^s U ° ) ² ) ex , ( 1 ⁺ a ( ^s U ° ) ² ) e y¹ )

из (26) в ряд Тейлора по степеням ( t -т )

при условии вt»1 и сохраняя два члена разложения, получим приближенные уравнения состояния оболочек [4]

CT x )

7 E T ( s x ) +^ 0 s y ) ) + P ^{1 -}^ 0

2 s (0 - 1 _e<0 + aU ( ^{1 )2} e (o) x    y    ux

CT y )

T E r ( ^sY+O 0 ^s x^{1 )} ) + P ^{2 s}Y ^{- 1 s1} + a ( ^s V)¹ e yV ) 1 -^ 0                    L 3 3 v /

где введен оператор P такой, что

P f

E

¹ + ^ 0

Гад f

Ip ² д7

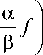
По найденным напряжениям (28) вычислим усилия и моменты [10]

h 0 /2                            h 0 /2                             h 0 /2                               h 0 /2

N = f ст, dz ,     N = [ ст dz ,     M_x = [ ст_х zdz ,     M = Г ст zdz

xx  yy  xx   y  yz

- h 0 /2                         - h 0 /2                          - h 0 /2                            - h 0 /2

и подставим (28), (29) в систему уравнений динамики оболочек [10]

д N

x дx

(д-Ц- = -rf p0"0 1Л     qx д t

д ² M x д x²

1 д Гд W

+ — N + — |-- N

R

д x l д x

^-p 0 ^h0V ^д^ ~Г = ^- d n ^{( - 1) 1} ' д t

.

Для исследования уравнений динамики вязкоупругих оболочек в (27)-(30) положим um- = s = o(1),  5m- = о(s),  a = O(s-1), a = O(1), « £1 = O(s),  RI = O(s1/2),  h^l = O(s).    (31)

l                      R ⁽¹⁾                                    P                p ² l                  l                     R ⁽¹⁾

Подставляя (7), (9), (10) в уравнения (27)–(30) с учетом оценок (31), получим нулевое приближение разложения по б — линейную систему уравнений, из которой следует связь wm   (i)

R ( i ) u 30

= Ц 1

um ^1 i а^

I ¹           \^a I /I     2/!       A»

^Ц 1 = I ^Ц 0 + тО ^{— Ц} 0⁾тт I / I ^{1 —} T⁽¹ — W^TT

V ³ p J/ V     ³          p .

и определяется безразмерная скорость волны

c

^{1 —} 3 ^{(1 — Ц} 0 ) e ^{(1 -Ц} 1²⁾ .

Из следующего приближения по б , с учетом (32) и (33), находятся уравнения для определения

Учитывая результаты, полученные ранее для q_x ^{( i )} , q_n , окончательно получим

( i ) u 10 .

д 2 и 10), + u m c д и ^ ^{д2 u (}0) д^дт l б 2 д^ д^ ²

,/^{д 11} )

V д^

11R i + -I — б V l V

I ² д и

J д^ ²

1² „2 c д ⁴ u (0)

I ^Ц 1 2 д^ ⁴

—

—

2 a I um- 1 (1 —Ц о )

3 б V l J

a 1 + ц/ + (1 + Ц 1 ) 4

e

c

1 ^a c₀                        2₂ д³ u ⁽0)

з-тО-m)»+Ц1+ Ц)т^т-+

+ ( — 1) ^{i — 1} -^{p l}—— 3ц, f 1 + 2ц, R I R fl^ u isl p ₀ h 0 5 c _о б ¹ V 5 J 5 V д^

—

д и1о   = о д^ J .

Легко видеть, что замена (22) позволяет записать систему уравнений (34) в виде дф(0 . ^дф0) дУ

+ 6 ф ⁽)        + 3

д t        др др

—

6 ^ 1 ( Ф ⁽ ' ) ) ²

дф ⁽ ' ) др

—

2 ( i )

= 2 д^-+иг ( ф ^(1> др

— ф ⁽²⁾ ) = 0.

Постоянные c ₁, c ₂, c ₃ определяются по формулам:

c ₁

1/3

1 1 1 ² 2

^c"> ^б

V R J c Ц 1

p l

V

c ₂=

Р о h 0 ^{5 c} 0 ^б

„ I          ^R I ^R

^{3 Ц} 1 I ¹ + ^2ц    I ,

V       5 J 5

c ₃

= 6 c 2 2l б c1 cum

.

Можно учесть,что 2 ц1 ^ » 1, и 1 отбросить. При этом вводятся обозначения

22 z _ cз c1 2 a | um | 6c,----— c 2 3 б V l J

^{(1 — Ц} 0 )

a 1 + ц/ + (1 + Ц 1 ) 4 в c

2 ^{1 a c} 0                        2x

^C 2 = ^c 1 7T2’T^{(1 — Ц} 0^{)(1 +Ц} 1 ^+Ц 1 ).

3 p l Б

Уравнение (35) полностью совпадает с уравнением (23), учитывающим конструкционное демпфирование материала оболочки. При описанном подходе нельзя полагать с ₂ = 0 ( a = 0), если сохраняется физическая нелинейность, и невозможно получить уравнения вида (24), так как в этом случае и с 1 = 0.

При ф ⁽¹⁾ =ф ⁽²⁾ уравнение (35) распадается на два одинаковых уравнения, представляющие собой модифицированное уравнение Кортевега-де Вриза–Бюргерса, имеющие точное решение

ф ^{( i )} =

3 — = 2

^/c 1 — 6 к^о" 1 ■ th | kx +

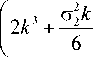
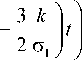
6 ст 1

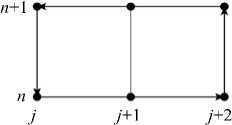
Рис. 1. Базовый контур для уравнения (40)

разностная схема метода конечных объемов, автоматически обеспечивающая выполненние интегральных законов сохранения по областям, составленным из базовых конечных объемов.

Для того чтобы воспользоваться предложенным подходом, запишем уравнение (35) в интегральной форме

J - (3 ф ⁽ ‘ ⁾² - 2 о 1 ф ⁽ ‘ ⁾³ + ф ⁽ ‘ ) _nn -ст ₂ ф ⁽ ‘ ) _n ) dt + ф ⁽ i ) d n + 30

+JJ(-1)*-1(ф(1) -ф(2))dtdn = 0 О для любой области О с контуром дО. Для перехода к дискретной формулировке сопоставим u(i)” = ф(i)(tn, Пj) и выберем в качестве базового контур, показанный на рисунке 1.

Добавим интегральные соотношения

J u(i),dt = u (i)(tn+1, n) - u(i)(tn, n), tn n J+1

J u ⁽ i\ d n = u ⁽ i ) ( t , n j +1 ) - u ⁽ i ) ( t , n j ),

n J

j

J ^{u nn d} n = ^{u (} i \ ⁽ t , n j +1 ) ^{- u( i )}n ⁽ t , n j )• n j

Используя для интегрирования по времени и четным производным по n формулу трапеций, а по нечетным производным по n формулу среднего значения, и полагая tn +1 - tn = т , nj+1 - nj = h , перепишем соотношения (40), (41):

3 n            n + + 1            1 n                n + + 1  \                   1 n            n + + 1             ->n                n + + 1\

3 u ^{( / )} J + 3 u ^{( / )} J - 3 u ^{( i )} J + 2 - 3 u ^<0 J + 2 I- o _x 1 2 u ^{( i )} J + 2 u ^{( i )} j - 2 u ^{( i )} j + 2 - 2 u ⁽ i ) j + 2 1 +

+(u(i) n + w(i) n+1 -w(i) n ,-u® n+1Л-а, (un n + uw n+1 -w(i) n , -uw n+HV- + nnJ       nnJ         nnJ+2       nnJ+2       2      nJ       nJ         nJ+2       nJ+2

+ ( u^{( i )} " +; - u^{( i )} " +1 ) ■ 2 h + ( - 1Г1 ( u ⁽¹⁾ n +1 + u ⁽¹⁾ " +1 - u ⁽²⁾ n +1 - u ) ■ h т = 0,

(i) n+1        (i) n т (i)n+1(

( u tj + u tj ) ■ 2 = u j ^- u j ,

(i) n (i) n h — ,,(i)n ,,(i)n u n J+1 u n J 2 u J+1 u J

• (i)    n 9 A — u( i) n(

nn J +1              n J +2        n J .

Вводя сеточные операторы сдвига 91, 0n по переменным t, n, соотвественно, запишем уравнения в операторной форме:

- (1 + 9 1 -9 n -9 1 9 n ) ° (3 u ⁾² -о , 2 u ⁽ⁱ⁾² + u ^'^ -o₂ u ^{( i )}n ) ■ ^ + + ( 9_n9 ₁ - 9_n ) ° u ^{( i )} ■ 2 h + ( 9_n9 ₁ +9_n ) ° ( - 1) i -¹ ( u ⁽¹⁾ - u ^<2) ) ■ h т = 0, ( 9 ₁ + 1) ° u^{( i )} _t -| = ( 9 ₁ - 1) ° u^{( i )} , ( 9 n + 1) ° u (i)^ h = ( 9 n - 1) ° u^{(i )} , 9 n ° u^{( i} V 2 h = ( 9 n - 1) ° u ^{( i )}n .

Выбирая допустимый лексикографический порядок, проведём сортировку сначала по функциям unn > un > ut > u , а затем по переменным 9n > 91. Таким образом построим базис Грёбнера или инволютивный базис [17]. В результате получим следующую разностную схему для уравнения (35), аналогичную схеме Кранка-Николсона для уравнения теплопроводности:

u ( i ) n ⁺¹ — u ( i ) "   , ( u ( i ) ² n +1 — u ( i ) ² " ч ) + ( u ( i ) ² n +i — u ( i ' ) „    ( u ( i ) ³ n +1 — u ( i ) ³ n +1 ) + ( u ( i ) ³ n +i — u ( i ) ³ " +i )

+3                                 +2g                                  + т                            4 h                       2                  4 h

( u ( i ) " +2 — 2 u ( i ) " ₊⁺1 + 2 u ( i j ¹ + u ( i ) " +2 ) + ( u ( i ) n+ 2 — 2 u ( i ) " ₊ 1 + 2 u ( i j + u ( i ) " —2 )

+--л--

4 h ³

⁺G 2

( u ( i ) n +1 + 2 u ( i ) " -¹ + u ( i ) "[ ) + ( u ( i ) n +1 + 2 u ( i ) n + u ( i ) n +1 )           1 u "> ■ +1 + u'" n+1 + u” > ■ +1 + u¹” - +,

= 0.

2 h                      ⁺ ( - 1)              2

Результаты проведенного компьютерного моделирования описываемых уравнениями (35) волновых процессов, возникающих в соосных облочках, содержащих в зазоре жидкость, представлены на рисунке 2 в виде графиков для безразмерных величин ф ⁽¹⁾ , ф ⁽²⁾ , определяющих продольную деформацию. Расчеты позволяют сделать следующие выводы:

• -    наличие жидкости между оболочками приводит к возникновению волны деформации не только во внешней оболочке, но и во внутренней, в которой в начальный момент деформации равнялись нулю (Рис. 2, б) ;

• -    во внешней и внутренней оболочках устанавливается волна деформации с постоянной амплитудой, скоростью распространения и локальным всплеском на переднем фронте, что соответствует решению типа «уединеной волны», которое не описывается аналитически.

Проведенные исследования направлены на развитие математических моделей, адекватно описывающих реологические свойства крови, лимфы и других биологических жидкостей. Использование данных моделей, в свою очередь, позволит существенно расширить возможности анализа экспериментальных данных по кровотоку, лимфотоку, пульсовым волнам и тому подобному, динамика которых носит существенно нелинейный характер, что имеет принципиальное значение для развития диагностических методов в современной медицине. Моделирование позволило выявить особенности поведения волн деформаций в геометрически и физически нелинейных вязкоупругих соосных цилиндрических оболочках, содержащих вязкую несжимаемую жидкость между ними.

Использование базиса Грёбнера для генерации разностной схемы при численном решении задачи Коши для системы двух нелинейных уравнений в частных производных третьего порядка по пространственной переменной позволило получить результат расчета без вычислительных осцилляций (см. Рис. 2).

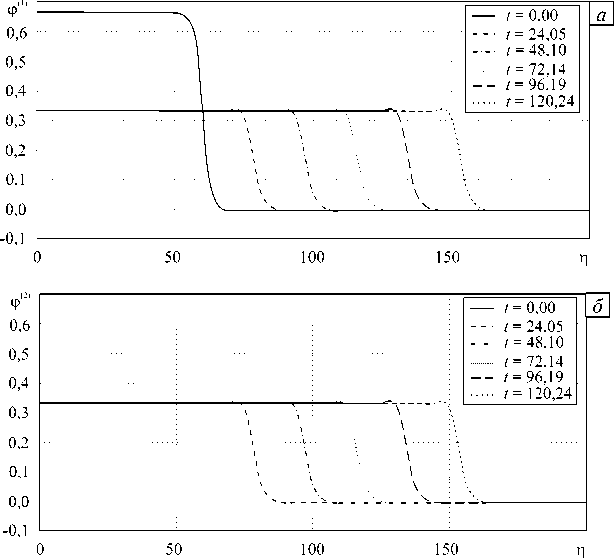
Рис. 2. График численного решения уравнения (35) с начальным условием (39) при g ₁=1,0, g ₂=1,0, к = 1/3 в различные моменты времени: ф ⁽¹⁾ ( а ); ф ⁽²⁾ ( б )

В результате возникает нелинейная волна деформации во внутренней оболочке, не имевшая место в начальный момент времени, и амплитуды волн деформации в соосных оболочках со временем начинают совпадать, при этом влияние жидкости постепенно исчезает. Совпадающие амплитуды в два раза меньше исходной амплитуды волны деформации внешней оболочки в начальный момент времени, а форма волны сохраняется. Эту конструкцию можно толковать как трехслойный пакет, заполнителем которого является жидкость.

Работа выполнена при финансовой поддержке РФФИ (проект № 13-01-00049-а) и гранта Президента РФ (проект МД-1025.2012.8).