Novel Approach of Designing Multiplier-less Finite Impulse Response Filter using Differential Evolution Algorithm

Published Online April 2012 in MECS

Finite duration Impulse Response (FIR) filter has found enormous applications in the field of communication and signal processing for a number of encouraging features associated with it like phaselinearity, guaranteed stability [1,2] etc. However, the applicability of this type of filter is heavily challenged by its equivalent Infinite duration Impulse Response (IIR) structure because of the hardware efficient construction of the latter [3,4]. Therefore in order to make FIR filter hardware friendly, a number of research articles have been published in the past [5-9] and a good number of works are still being carried out.

Different approaches have been proposed in the literature for reducing the computational complexity of FIR filter. However, major emphasis has been put forward by quantizing each of its impulse response coefficient by means of sum of power of two (SPT) terms, as far as the survey result of hardware efficient FIR filter design is concerned [10-12]. This special architecture enables the FIR filter to carry out the operation of multiplication only through the use of delay elements and adders and thus reduces the hardware complexity significantly.

The area of signal processing and mostly the design of digital filter is being currently influenced by a number of evolutionary computational mechanisms. The success of these schemes over orthodox optimization technique has already been firmly established in [13] which has inspired the researchers to think about intelligent optimization to be deployed in wide area of science and engineering. As a matter of fact, the techniques like Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Differential Evolution (DE) have been popularly used in designing FIR and IIR filter over the last few years or so [14-17]. Amongst them, DE has particularly developed unique interest amongst researchers because of its inherent simple yet effective construction along with its limited number of control parameters [18-22]. This has triggered the applicability of DE even if in most challenging scenarios.

Proper selection of filter hardware is necessary for building the designed system robust against any impairment. Therefore the optimization between the system complexity and achievable response is a matter of great concern to the system designers and thus demands for considerable attention. DE, being a powerful evolutionary optimization tool, combined with the concept of coefficient quantization has been jointly exploited in this paper to minimize the required hardware of FIR filter. The impact of filter order and total number of quantization levels on its response have been examined thoroughly by considering different values for those parameters. Finally, the proposed architecture has been designed using VHDL code and subsequently been compared with other discrete coefficient existing FIR models to prove the superiority of our algorithm.

The entire paper has been organized as follows: Section II briefly describes the theory behind DE with a special emphasis to each of its different steps. Section III demonstrates the proposed novel algorithm with significant mathematical explanations. Simulation results and critical analysis with other state-of-the-art techniques have been illustrated in Section IV, followed by a conclusion in Section V.

• II.    Theoritical Background of Differential Evolution Algorithm

  Differential Evolution (DE) algorithm has emerged as a very competitive form of evolutionary computing for more than a decade ago. The first written article on DE appeared as a technical report by R. Storn and K. V. Price in the year 1995 [19]. In quick times, DE has turned out to be one of the best evolutionary optimization algorithms for solving real valued test function. Afterwards, researchers have carried out a number of modifications on classical DE to come up with techniques like Fuzzy Adaptive DE (FADE) [23], Self Adaptive DE (SADE) [24], Opposition-based DE (ODE) [25], DE with global and local neighborhoods (DEGL) [26] , JADE [27] and so on which prove themselves to be superior to conventional one in various respects.

DE is very simple yet robust, powerful, stochastic, population based and easy to use optimization algorithm, which has been developed to optimize real parameter and real valued functions. General problem formulation for DE is for an objective function f:R^D ^R ; the proper selection of x*e X such that f (x*) (x) for all xe X .The distinct idea behind DE is a new scheme for generating trial parameter vectors x . Therefore this algorithm can optimize any function with D real parameters for any positive integer number D. Before the execution of the algorithm, size of the population should be selected properly. Population size (P) does not change during the minimization process.

The name of the algorithm is chosen as Differential Evolution (DE) to signify a special type of differential operator in it that has been utilized to create new offspring from the parent chromosomes without adopting classical crossover or mutation. By performing an extensive test bed it has been found that this optimization technique converges at a faster rate than any other globally acclaimed optimization techniques [20-21]. DE can be implemented very easily using very few parameter tuning which makes the algorithm reasonably popular very soon.

Differential Evolution algorithms can be divided into four steps, namely Initialization, Mutation, Recombination, and Selection.

• A. Initialization

This step indicates the beginning of the search algorithm. Initially, the values of the parameter vector are chosen randomly in such a way that it can cover the entire parameter space. In case the distribution of random variable is unknown, uniform probability distribution for random variables is normally assumed without the loss of any generality. For x^ denoting the Ith element of the jth member of population at first iteration, its value must be within the upper and lower bound of the random variable and can be written as [18, 22]:

x^L<х_идu (1)

B.Mutation

The step of mutation actually expands the search space by evolving offspring from the parents. However, unlike traditional Evolutionary Algorithms (EA), the DE variants perturb the population members of current generation with the scaled differences of randomly selected and distinct population members from the previous generation. Therefore no separate probability density function has to be used for generating the offspring [18].

Specifically, from the i^th member of the current population x t^ , a mutant or donor vector v_t , _G+1 is created in the process of mutation. Depending upon the generation of the donor vector from the parameter (or target) vector, different variants of DE has been developed.

The general convention used in the literature is DE/p/q/r, where p represents a string denoting the vector to be perturbed, q is the number of difference vectors considered for perturbation of r stands for the types of crossover being used i.e. either exponential or binomial.

In the DE/rand/1 scheme the mutant vector of the next generation v_tiG+1 is generated according to the following equation [18-20]:

V t⁽ G + l) rand/1 = ^xP1^(G) +F. ^[xp ₂ ⁽G) ^-xp ₃(G ^)]

Here F is called the Weighting Factor and running index 'i ' is different from other three indices like p 1 , p₂ and p 3 . Consequently, DE scheme requires minimum 4 no of population for every iteration.

DE/rand to best/1 follows the same procedure as that of DE/rand/1. The only difference is that the donor vector v_ti G ₊₁ is created using any two randomly selected parameter vectors and the best member of the current generation. Mathematically, this can be outlined as follows [22, 25]:

V [^(G + V) randtobest/1

= x_i(G)+A.[x_bes t (G)-x_i(G)] ⁺ F. [ ^xp1^{(G) -x}p ₂ ^(G)]

For the scheme of DE/best/1 and DE/best/2, donor vector of any generation can be generated without using the corresponding parameter vector. The mutant vectors for these two schemes can be written respectively as [2326]:

V t (G + l) best/i ^{— x}best^(G) + F. [x_pl(G) ^- x_p2(G)]

V [^{(G + 1)}best/2 ^{— x}best^{(G) + F} . ^[xpl^{(G) + x}p2^(G) -x_p3(G) - x p4 (G)]

In (4) and (5), x_best (G) identifies the member from the G^th generation which shows the maximum fitness. The concerned population member 'i ' and the four other members from the same generation i.e. p 1 , p 2 , p 3 and p 4 are entirely different from each other.

For the scheme of DE/rand/2, in order to construct donor vector, five such distinct parameter vectors and two Weighing Factors ( F_l , F₂ ) are needed. The equation governing the generation of mutant vector is having the form [18, 22]:

^ i⁽ G + 1) rand/2 —X pi⁽ G) + F i .[X p2⁽ G)

-X p ₃(G)]+F 2 .[X p4 (G)-X p _S(G)]

C. Recombination

Recombination incorporates successful solutions from the previous generation. It plays a significant role to increase the potential diversity of the population member. At the end of this step, the trial vector u_i , _G+l is developed from the elements of target vector x^_G and the elements of donor vector v^_G+l. Elements of donor vector enter the trial vector with probability CR. The trial vector can be constructed according to the following equation [19-21]:

u_M(G + 1) — [

' ?ц(6 + 1); rand ji rand V ij (G + 1); rand ji >CR andj * I rand

In the above equation, rand ji is a random value in the range [0, 1] and I_rand is a random integer from [1, 2…….D]. CR denotes recombination or cross-over probability and certainly is in the range [0, 1]. This, in turn, makes sure that the trial vector u_i , _G+l gets at least one parameter from the mutant vector v_i ^ _+l .

D. Selection

This is the final step of the evolutionary algorithm. Comparing the values of trial vector u_iiG with the target vector x_iG it can be decided whether or not the trial vector will be able to be a member of the next generation. This can be mathematically formulated as follows [25,26]:

x ; (G + 1) —

fu j (^G + ^1); 5(u i (^{G + 1}))<5(^x i (^{G + 1}))

I x i (G);         ^(x_i(G⁾)>l(x_i(G + 1⁾)

Where 3(Y_i(G)) identifies a cost function related to the problem of interest associated with the i^th vector Y_i(G) at iteration ‘G’.

If the trial vector u_iiG+l yields smaller cost function than target vector x_i , _G then the value of trial vector is assigned to x^_G+l ; otherwise the old value of the target vector will be sustained. Mutation, Recombination and Selection process will continue until any termination criteria is reached. If the termination criteria can not be achieved even after the execution of maximum number of iterations, the member of the population having the least functional value is chosen as the optimized solution to the concerned problem.

• III.    Mathematical Formulation of the Proposed Approach

This work actually deals with designing a discrete coefficient FIR filter under several constraints like maintaining the required specification of filter response as specified by user, using minimum number of hardware elements, minimizing the number of non-zero coefficient in the impulse response and so on. In connection to multiplier-less filter design, an L-length FIR filter with power of two coefficients may be mathematically represented as:

W — Z£;0ckn2-k , n — 0,1,2.......L - 1 (9)

In the above equation, the term ‘Δ’ , also called word length (WL) of filter coefficient, gives a measure of the total number of quantization levels used during the process of quantization and c _kn is nothing but a binary mask for generating the discrete coefficients from a limited set of values available for construction. For a particular sample n 0 , this may have the form as:

^Cn₀ ^— [ ^co,n_o ^cl,n₀^c2,n₀ .....^сД,п₀ ]; ^ck,n₀ ^B ^{— {} 0, ^1} , ke {0,1,.....,Д - 1} and n_o e {0,1,.....,L - 1}

Hence the proper assignment of individual c_{kn o} is the key that governs the frequency characteristics as well as the hardware requirement of the FIR filter. More interestingly, these two issues are contradictory to each other and thus require thoughtful and logical considerations. For a fixed Δ, there are 2^Δ numbers of all possible combinations of mask vectors in a set M, all of which may or may not be required for constituting the final response. This necessitates a search for obtaining the most favorable collection of mask vectors [C_k , _n] V k e {0,1,2, ,Д - 1} and ne {0,1, ,L - 1} from the set M.

In recent years, the approach for searching the most suitable vectors from a collection of potential vectors has been modified tremendously through the innovation of a number of artificially powerful mechanisms. Amongst them evolutionary computation demands for particular concentration because of its several attractive attributes. This study involves one of the most popularly employed evolutionary techniques, named as Differential Evolution (DE), for optimizing the discrete FIR coefficients. By using general notation, this may simply be outlined as:

h Lpt (n) = 0[cX „ ] = 0[2_k{h^L(n)}];

V k e {0,1,2,.....,Д - 1} and ne {0,1,.....,L - 1} where the symbols О and 2 signify the optimization and quantization operations respectively.

Interchanging the order of operations in (11) can sometimes be regarded as an alternative approach of having optimally selected discrete coefficient FIR filter. The necessary design rule has been outlined as:

h Lpt (n) = 2_k№^L(n)}];

V k e {0,1,2,.....,Д - 1} and ne {0,1,.....,L -1}

One prominent difference can be pointed out between the two optimization approaches as described in the above equations, namely Approach 1 (Quantization prior to optimization) and Approach 2 (Optimization prior to quantization). In (11), optimization is performed on already quantized coefficients and thus through the process of optimization it has the effect of reducing the initial quantization error incurred at the very beginning. Therefore, the optimum outcome is expected to approximate the ideal or near-ideal solution in an accurate sense. However, approach 2 begins with optimizing the filter coefficient and is incorporating the quantization process at the final stage. Therefore it suffers from serious quantization error which has almost no chance to get minimized. On the other hand, approach 2 may provide some coefficient value less than 2- (Δ-1) after carrying out the search mechanisms. After passing through a uniform quantizer, they would finally result in zero-valued coefficients and therefore reduce the hardware cost noticeably.

Nevertheless, both of these two procedures call for applying an optimization over a Δ (for approach 1) or L (for approach 2) dimensional search space. The use of Differential Evolution (DE) optimization for this specific purpose additionally includes some fundamental steps, more commonly observed in any evolutionary programming, like initialization, mutation, cross-over or recombination and selection. The potential solution vector X f V i e P of the concerned problem is accepted in the process of initialization from a D-dimensional search space ^^D where P is the set of population members and D is either equal to Δ or L, depending upon the selected approach.

The immediate next step of initialization is called mutation in which the entire search region is explored intensively. The mutant vector for the next generation Y^1 is generated from the parameter vector Xp of the current generation. The mutant vector further undergoes through the process of cross-over (recombination) and selection to finally end up with the potential parameter vector for the next iteration. However, the creation of parameter vector for the next iteration from that of present generation is largely monitored by the rules adopted during mutation, cross-over and selection. Thus for kth mutation rule, lth cross-over rule and mth selection scheme; the formal mathematical notation of evolutionary optimization mechanisms can be described V i e P and V у e G as:

mJxf^Y^1(13)

6i[Yis+1]=Zf+1(14)

@m[xf,Zf+1]=Xf+1(15)

Use of DE under scheme 1 would result in an optimally selected binary matrix Copt whose each row identifies the mask coefficient for a single coefficient of impulse response, as shown in the following equation:

,where the asterisks stands for optimization.

In (13), each of C J V i e {0,1,2,.....,L - 1} is a row vector having Δ elements. However, optimization under scheme 2 only considers L-dimensional vector as its agents and therefore would result in an optimum solution as:

M_op t = [h f h l h ..... h^]                 (17)

• IV.    Results

In this work, a recent population based optimization algorithm has been used for the coefficient quantization of low-pass FIR filter. As any population-based strategy consumes considerable amount of time in locating the optimum solution, the researchers have placed their doubts in incorporating such methods in practical signal processing applications. This has been one of the biggest challenges for us particularly when it is applied for the purpose of reducing the computational complexity. The inclusion of DE in this specific problem of signal processing has been justified by showing the variation of averaged cost function with the number of iterations for two different approaches in Fig. 1, keeping the size of population fixed at 100.

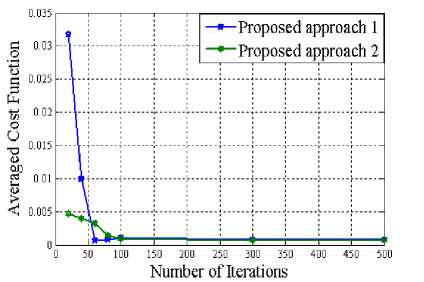
Figure 1. Convergence behavior of proposed approaches

From the plot of Figure 1, it can be clearly inferred that our proposed method does not necessitate the use for a significantly large number of iterations to converge. More specifically, around 60 (for approach 1) and 100 (for approach 2) iterations are needed for locating the most favorable solution. Although, the initial cost function is comparatively large for approach 1, it diminishes abruptly beyond a certain number of generations. Therefore, the possibility of not finding the optimal solution through our proposed approaches does not arise at all.

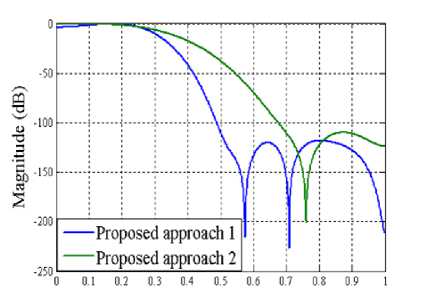
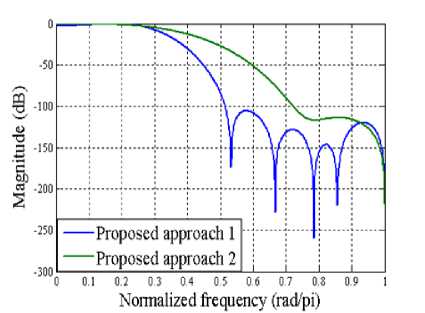
After comparing the two approaches of discretecoefficient FIR filter design by means of their computational time; the quality of the solution obtained by them is another important issue to be addressed. The resulting frequency response of the proposed multiplierless FIR filter, achieved through two different approaches, has been plotted in Figure 2 for three distinct lengths of the filter. The word length of the impulse response coefficient has been kept at 8 to show the competency of our proposed algorithm to exhibit the required specification even with a smaller WL. The pass-band and stop-band edge frequency are located at 0.25 rad/pi and 0.5 rad/pi respectively and the allowable pass-band ripple and stop-band attenuation has been selected as 1 dB and 50 dB respectively in the entire design.

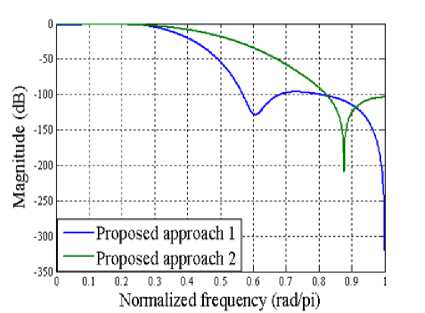
(a) Length=15

Normalized frequency (rad/pi)

(c) Length=29

Figure 2. Frequency response of the designed filter (WL=8)

It can be unambiguously noticed that irrespective of the filter order, the proposed approach 1 which involves quantization prior to optimization would result in better frequency response, particularly in the transition and stop-band region, as compared to approach 2. Additionally, the pass-band responses of designed filter remain almost identical regardless of the sequence of selecting optimization and quantization. The numerical values of transition-band and stop-band attenuation has been listed in TABLE 1 at some distinct frequency points for three different length of multiplier-less low-pass FIR filters, considered in this paper.

TABLE 1. Numerical values of Attenuation in db

Length		15		22		29
Approach		1	2	1	2	1	2
Frequency points (rad/pi)	0.3	5.092	3.349	7.723	4.934	10.3	6.471
	0.4	20.19	8.633	30.24	12.72	40.93	17.32
	0.5	53.59	18.46	83.35	27.07	109.4	37.31
	0.6	127.4	34.32	108.2	51.09	133.3	69.58
	0.7	97.59	57.67	131.2	90.1	154	110.3
	0.8	99.96	90.38	155.1	116.5	118.3	122.3
	0.9	114.7	124.8	126.1	116	128	111.2
	1.0	319.7	103.9	207.6	217.8	210.7	123.6

(b) Length=22

The numerical entries of TABLE 1 firmly establish the superiority of approach 1 than approach 2 in designing low-pass FIR filter, as far as their transition and stopband attenuation values are concerned. However, the selection of suitable filter order seems to be an essential issue since the choice of higher order filter always costs more hardware usage. In addition to this, for a particular filter order, the choice of word length plays an essential role in determining associated hardware cost. Higher the word length, more is the accuracy and thus demands more hardware elements. The impact of these two factors on the hardware complicacy has been thoroughly studied in this work by considering three different lengths and four distinct word lengths for each of the three lengths examined in this paper.

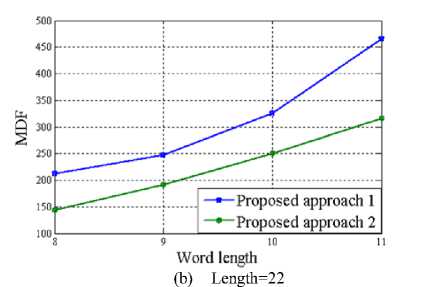
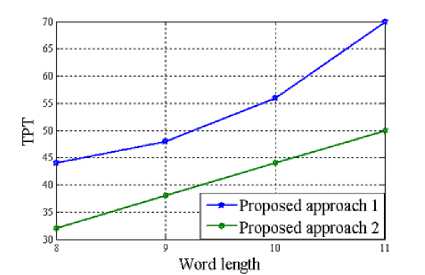
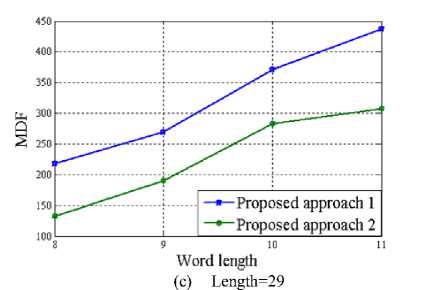
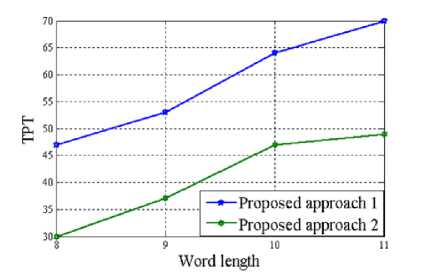
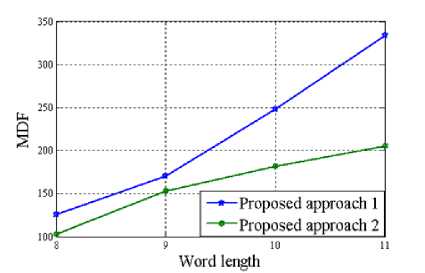
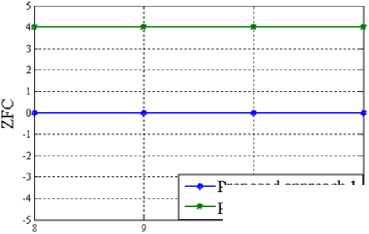
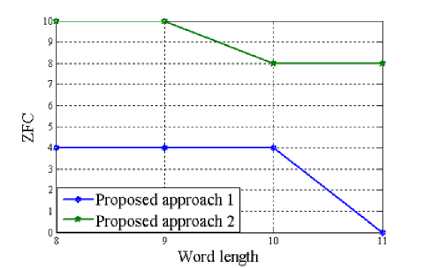
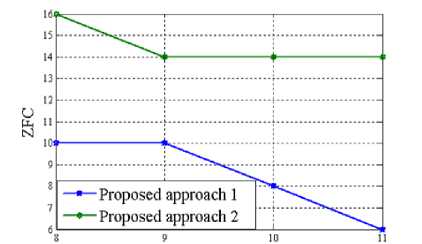
Since the proposed multiplier-less FIR filter has been implemented by means of sum of power of two (SPT) terms; a number of performance parameter has been taken into account for calculating the associated hardware cost of the design. This includes total number of power of two terms (TPT), multiplier delay flip-flop (MDF), multiplier adder (MA) and zero-valued filter coefficients (ZFC). The variation of these parameters with the word length of the FIR filter has been presented pictorially in Figure 3 through 6 for length 15, 22 and 29 of the designed filter respectively.

Proposed approach 1

Proposed approach 2

9                         10

Word length

(a) Length=15

(b) Length=22

(c) Length=29

Figure 3. Variation of TPT with Word length of the proposed multiplierless FIR filter

(a) Length=15

Figure 4. Variation of MDF with Word length of the proposed multiplier-less FIR filter

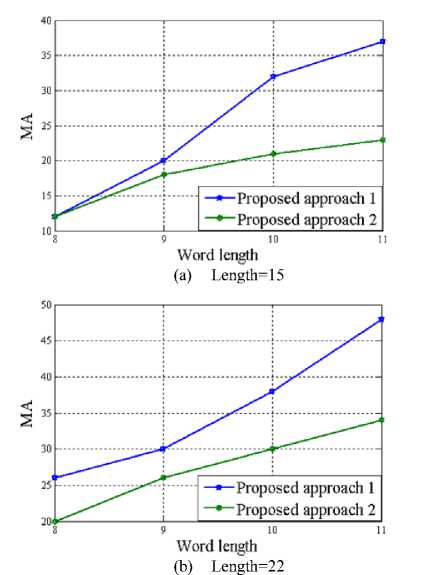
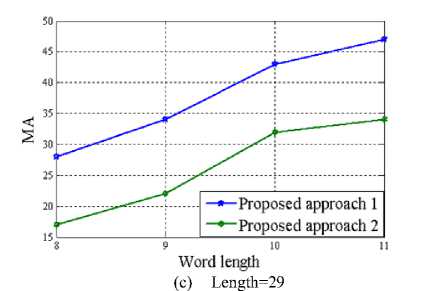
Figure 5. Variation of MA with Word length of the proposed multiplierless FIR filter

Proposed approach 1

Proposed approach 2 io

Word length

(a) Length=15

(b) Length=22

and MA when compared with approach 1 for any specific value of word length. Total number of zero-valued filter coefficient (ZFC) in the impulse response also serves as a useful measure in evaluating its performance for high speed application. As obvious, more ZFC implies less mathematical computations and thus supports the designed architecture to be employed in complicated circuits. Approach 2 continues to outperform approach 1 in connection to this parameter also; as it always incorporates more ZFC than our first approach by a considerably large margin.

While dealing with the design of hardware efficient multiplier-less FIR filter structure in this work, the requirement of different types of hardware blocks has been treated as a useful measure for comparing their architectures. Since the conventional multipliers of filter model have been eliminated by simpler structures in this particular design; the requirement of alternative hardware for multipliers like delay elements, full-adders and subtractors may become helpful in evaluating the hardware complicacy of the designed filter. In order to critically analyze the system complexity from this viewpoint, the proposed filter along with the other existing multiplier-free FIR filters have been developed by means of hardware description language. The VHDL code has been synthesized using Xilinx Synthesis Technology (XST) with a product version of ISE 12.3 and executed in Intel(R) Core(TM) i3 processor with 2 GB RAM and 32-bit operating system. To be specific, the hardware cost of the proposed multiplier-less filter of length 22 and 29 have been subsequently been compared with that of other existing multiplier-free FIR models of same or approximately same length. The summary of the entire synthesis report has been listed in TABLE 2 and TABLE 3 respectively.

Word length (c) Length=29

Figure 6. Variation of ZFC with Word length of the proposed multiplier-less FIR filter

TABLE 2. Comparative Analysis Amongst Various Multiplier-free FIR Filters In Terms of Hardware Cost After Realization Through XST (Length of the Proposed Filter=22)

Method	Word length	I/O Buffer	Full adder	Subtractor	Delay
Kaakinen [8]	10	3	17	1	25
Yu [9]	9	3	14	1	27
	10	3	17	1	25
	11	3	20	1	26
Proposed approach 1	8	3	9	1	26
Proposed approach 2	8	3	9	1	23

Looking at the above diagrams, the supremacy of approach 2 can well be revealed as far as their design complexity is concerned. Figure 3 to 5 clearly indicate that approach 2 is always in need of fewer TPT, MDF

TABLE 3. Comparative Analysis Amongst Various Multiplier-free FIR Filters In Terms of Hardware Cost After Realization Through XST (Length of the Proposed Filter=29)

Method	Word length	I/O Buffer	Full adder	Subtractor	Delay
Saramaki [5]	11	3	14	1	39
Yao [6]	13	3	18	1	38
Jheng [7]	12	3	17	1	39
Proposed approach 1	8	3	14	1	30
Proposed approach 2	8	3	11	1	27

Looking at the numerical entries in the above tables, a number of promising outcomes can be drawn. Critical analysis of these experimental findings reveal the hardware efficiency of the proposed design in a better way. It can be well observed that blocks like I/O buffers and subtractors remain fairly insensitive to the choice of the adopted method of designing hardware friendly FIR filter along with their specifications. However, the usage of full adder and delay elements seems to be a determining factor in selecting the suitable filter architecture. In connection to this, our approach of favoring optimization techniques like Differential Evolution (DE) in finding the optimal filter coefficients proves itself to be very much proficient than other state-of-the-art conventional approaches. Irrespective of the filter length, both of our approaches require less number of full adders and delay blocks than other promising findings available in literature. It has already been demonstrated previously in this article that our second approach proves to be more hardware efficient than the first one while the later exhibits better low-pass characteristics than the former. This inspection proves to be accurate after the realization of the designed filters through XST. Additionally, the significant contributions made by the above two tables lies in the fact that the process of quantization prior to optimization, i.e. approach 1, apart from showing better low-pass nature results in a FIR filter design which outperforms the other existing models in terms of hardware complexity as well. If further reduction in hardware seems to be essential, then one can think about incorporating approach 2 in this regard.

• V.    conclusion

System designers often face problems in realizing complicated digital circuits as trade off between system complexity and achievable performance becomes inevitable. In this paper, two flexible approaches have been adopted by incorporating Differential Evolution algorithm for designing multiplier-less low-pass FIR filter. Experimental results reveal the pre-eminence of the proposed design strategies over the existing techniques from two different angles. Both of the proposed methods for designing multiplier-free FIR filter proves themselves to be superior than many existing well-recognized approach of such design. In addition to this, the proposed technique imposes a flexibility between obtainable response and necessary hardware requirement and therefore emerges as a challenging solution in the area of multiplier-less FIR filter design.