Новые подходы к оценке и прогнозу заболеваемости энтеровирусной (неполио) инфекцией в Российской Федерации с использованием математических моделей

Глобальной проблеме изучения энтеровирусной (неполио) инфекции (ЭВнИ) уделяется большое внимание [1, 2]. Ей посвящены работы ведущих отечественных и зарубежных ученых1 [3, 4]. Мировой и российский опыт, объем накопленных знаний ставят вопросы научного и рационального использования их для эффективного воздействия на эпидемический процесс. Значимость ЭВнИ определяется высокой интенсивностью, повсеместным распространением, высокой долей вспышечной заболеваемости, конта-гиозностью и летальностью [5–7], высокой устойчивостью неполиомиелитных энтеровирусов (НПЭВ) во внешней среде [8], отсутствием средств специфической профилактики [9, 10]. В Российской Федерации эпидемиологический надзор за ЭВнИ регламентируется санитарными правилами «Профилактика энтеро-вирусной (неполио) инфекции»2 и методическими указаниями «Эпидемиологический надзор и профилактика энтеровирусной (неполио) инфекции»3. До 2017 г. реализованы две ведомственные целевые программы Роспотребнадзора, в настоящее время осуществляется программа на 2018–2022 гг.

Однако динамика заболеваемости ЭВнИ в РФ до настоящего времени имеет существенную тенденцию к росту. По мнению одних авторов, это связано со сменой доминирующих вирулентных вариантов НПЭВ [11, 12], по мнению других - с улучшением регистрации заболеваемости и качества лабораторной диагностики⁴ [13].

Таким образом, разработка новых подходов к изучению заболеваемости ЭВнИ приобретает для РФ особое значение [14–17]. Отчетливой и значимой задачей в совершенствовании эпидемиологического надзора в части совершенствования его информационной подсистемы является широкое использование методов математического моделирования [18, 19].

Цель исследования – изучить основные проявления эпидемического процесса энтеровирусной (не-полио) инфекции в Российской Федерации за 14 лет (2006–2019 гг.) с использованием математических моделей.

Материалы и методы. Базой для анализа заболеваемости ЭВнИ за указанные период явились: форма федерального статистического наблюдения ф. № 1 «Сведения об инфекционных и паразитарных заболеваниях», месячная; форма федерального статистического наблюдения ф. № 2 «Сведения об инфекционных и паразитарных заболеваниях», го-довая⁵.

В работе использованы описательно-оценочные эпидемиологические методы исследования (статистическое наблюдение, основанное на изучении отчетно-учетной документации, ретроспективный эпидемиологический анализ). В ходе ретроспективного эпидемиологического анализа изучены абсолютные показатели заболеваемости населения, интенсивные показатели заболеваемости энтеровирусными инфекциями (случаев на 100 тысяч населения), интенсивность эпидемического процесса, многолетняя и внутригодовая динамика. Для расчета интенсивных показателей использовали данные Федеральной службы государственной статистики о численности населе- ния, опубликованные в Единой межведомственной информационно-статистической системе (ЕМИСС)6.

Для построения линий трендов подбор коэффициентов в математических моделях определяли по методу наименьших квадратов. Использовали перечисленные ниже аппроксимации:

• –    линейная: y = a · x + b ;

• –    логарифмическая: y = a · Ln ( x ) + b ;

• –    степенная: y = bx^a ;

• –    экспоненциальная: y = b · e^{a · x} ;

Подбор оптимальной математической модели осуществляли с использованием трех статистических показателей: коэффициента детерминации, критерия Фишера, стандартной ошибки для оценки y .

Для оценки выраженности тенденций эпидемического процесса в многолетней динамике использовали показатели среднегодового темпа прироста. В связи с тем что рассматриваемые временные ряды не превышали 14 наблюдений (период наблюдений 14 лет), применяли методы непараметрической статистики. Наличие и степень линейной зависимости между двумя множествами данных рассчитывали с помощью коэффициента корреляции Спирмена. Периодичность подъемов и спадов заболеваемости была наглядно продемонстрирована с использованием периодограмм и рассчитана с применением одномерного спектрального анализа Фурье. При высокой корреляции (коэффициент при определенном синусе или косинусе) можно сделать выводы о наличии строгой периодичности в данных, на соответствующей частоте. Поскольку функции синусов и косинусов независимы (или ортогональны), можно арифметически сложить квадраты коэффициентов для каждой частоты, чтобы получить искомую периодограмму.

Значения периодограммы можно интерпретировать как дисперсию (вариацию) данных на соответствующем периоде. Значения периодограммы (на оси ординат) вычисляются как:

22 N

Pk = sin-коэффициентk + cos-коэффициентk ■ —, где синус, косинус - функция циклической компоненты временного ряда; Pk - значения периодограммы на частоте vk, и N - общая длина ряда. Для наглядности частота на оси абсцисс преобразована в период: Tk = 1/vk. Расчет коэффициентов производился путем построения модели линейной множественной регрессии, где зависимая переменная – наблюдаемый временной ряд, а независимые переменные или регрессоры – функции синусов всех возможных (дискретных) частот. Наиболее эффективным решением данной задачи и явился алгоритм быстрого преобразования Фурье.

Внутригодовую динамику заболеваемости ЭВнИ оценивали на основании помесячного распределения случаев заболеваний на территории Российской Федерации в период наблюдения с 2013 по 2019 г. Для расчета эпидемического порога использовали методику, предусмотренную МР 3.1.2.0118-17.3.1.2⁷. Для анализа временных рядов ежемесячной заболеваемости – классическую сезонную декомпозицию – метод Census I. В основе метода лежит предположение, что временной ряд включает в себя четыре различные компоненты: сезонная компонента (обозначается St , где t – момент времени), тренд ( Tt ), циклическая компонента ( Ct ) и случайная, нерегулярная компонента, или флуктуация ( It ). Разница между циклической и сезонной компонентой состоит в том, что последняя имеет регулярную (сезонную) периодичность, тогда как циклические факторы обычно обладают более длительным эффектом, который к тому же меняется от цикла к циклу. В методе Census I тренд и циклическую компоненту обычно объединяют в одну тренд-циклическую компоненту ( TCt ). Конкретные функциональные взаимосвязи между этими компонентами могут иметь самый разный вид. Однако можно выделить два основных способа, с помощью которых они могут взаимодействовать: аддитивно и мультипликативно:

• –    аддитивная модель: Xt = TCt + St + It ,

• –    мультипликативная модель: Xt = Tt · Ct · St · It , где Xt обозначает значение временного ряда в момент времени t .

В вычислительном отношении процедура метода сезонной декомпозиции (Census I) следует стандартным формулам [20].

Результаты и их обсуждение. По данным официальной статистики заболеваемость ЭВнИ в РФ за 14 лет (2006–2019 гг.) характеризовалась неравномерным распределением и выраженной тенденцией к росту (рис. 1).

Среднемноголетний уровень (СМУ) составил 7,25 ⁰/ 0000 (СКО = 4,1 ⁰/ 0000 , медиана 5,9 ⁰/ 0000 , межквартильный интервал от 4,28 ⁰/ 0000 до 9,82 ⁰/ 00000 ), среднегодовой темп прироста 4,4 % (угол наклона линейного тренда 34 ° ). Подъемы заболеваемости зарегистрированы в 2009 г. (4,72 ⁰/ 0000 ), в 2013 г. (11,22 ⁰/ 0000 ) и в 2017 г. (16,32 ⁰/ 0000 ), при этом каждый последующий подъем превышал предыдущий. Возникновение локальных минимумов регистрировали в 2010 г. (2,91 ⁰/ 0000 ), в 2014 г. (6,35 ⁰/ 0000 ) и в 2015 г. (5,36 ⁰/ 0000 ).

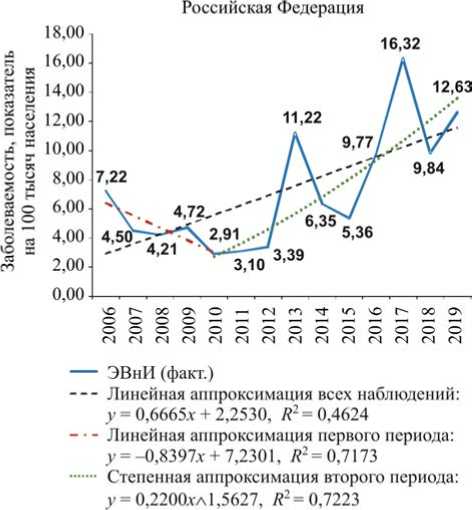
Рис. 1. Многолетняя динамика заболеваемости энтеровирусной (неполио) инфекцией в Российской Федерации (2006–2019 гг.), случаев на 100 тысяч населения

Использование стандартного эпидемиологического подхода к оценке заболеваемости для изучаемого периода времени свидетельствовало о том, что применяемые математические модели (линейная, логарифмическая, степенная, экспоненциальная) неудовлетворительно аппроксимировались на данный временной ряд (табл. 1) и свидетельствовали как минимум о двух периодах с разнонаправленными трендами.

По нашему мнению, это обусловлено тем, что начиная с 2009 г. в РФ изменились подходы к регистрации случаев ЭВнИ, поскольку с вступлением в силу МУ 3.1.1.2363-088 стало обязательным лабораторное подтверждение не только групповых, но и спорадических случаев заболевания, что отразилось на качестве лабораторной диагностики ЭВнИ. Исходя из этого, приемлемую математическую модель, определяющую направление и темп роста заболеваемости, можно получить, разбив временной ряд на два периода (относительно минимального показателя в 2010 г. ‒ 2,91 0/0000). Первый период с 2006 по 2010 г., второй ‒ с 2010 по 2019 г. При этом для оценки заболеваемости выбран временной отрезок с 2010 по 2019 г. как более оптимально соответствующий уровню заболеваемости по степенной аппроксимации (табл. 2).

С учетом недостаточно большого 9-летнего (2010–2019 гг.) периода наблюдения показательными величинами описательной статистики были приняты величина медианы заболеваемости, которая составила 6,35 ⁰/ 0000 , и межквартильный интервал ( IQR ) с диапазоном 3,38–9,84 ⁰/ 0000 .

Анализ заболеваемости с использованием данного подхода установил, что среднемноголетний уровень заболеваемости ЭВнИ в РФ составил 8,09 ⁰/ 0000 , среднегодовой темп прироста – 17,7 % (угол наклона линейного тренда 50 ° ). В соответствии со степенной функцией развитие эпидемического процесса ЭВнИ в этом периоде характеризовало его как неуправляемый и предполагало неблагоприятный прогноз.

Таблица 1

Математические модели динамики заболеваемости энтеровирусной (неполио) инфекцией в Российской Федерации (2006 – 2019 гг.)

Тренд	Математическая модель	Коэффициент детерминации R 2	F -критерий	Стандартная ошибка для оценки y
Линейная аппроксимация	y = 0,6665 x + 2,2530	0,4624	10,3216	3,1292
Логарифмическая аппроксимация	y = 2,6436Ln ( x ) + 2,4950	0,2491	3,9807	3,6982
Степенная аппроксимация	y = 3,5140 x 0,3228	0,2027	3,0514	0,5158
Экспоненциальная аппроксимация	y = 3,2716e0,0870 x	0,4298	9,0461	0,4362

Таблица 2

Математические модели динамики заболеваемости энтеровирусной (неполио) инфекцией в Российской Федерации (2010–2019 гг.)

Тренд	Математическая модель	Коэффициент детерминации R 2	F -критерий	Стандартная ошибка для оценки y
Линейная аппроксимация	y = 1,1757 x – 3,0816	0,6055	12,2809	3,0473
Логарифмическая аппроксимация	y = 10,4144Ln ( x ) – 14,8374	0,6054	12,2759	3,0477
Степенная аппроксимация	y = 0,2200 x 1,5627	0,7223	20,8058	0,3513
Экспоненциальная аппроксимация	y = 1,3230e0,1732 x	0,6966	18,3699	0,3671

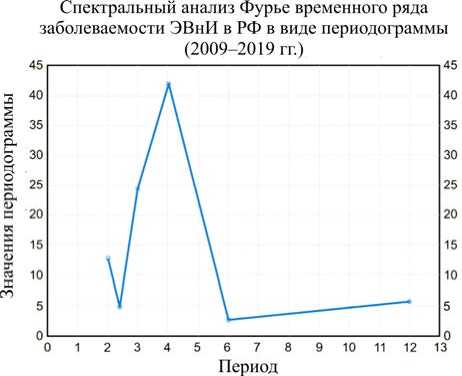
Рис. 2. Периодограмма заболеваемости энтеровирусной (неполио) инфекцией в Российской Федерации (2009–2019 гг.): ось OX – периодичность в годах, ось OY – дисперсия данных на соответствующем периоде

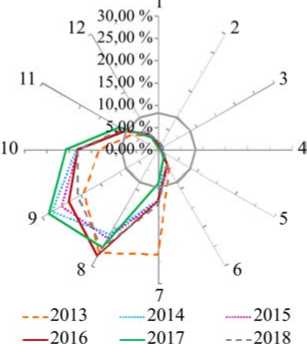
Рис. 3. Внутригодовая динамика энтеровирусной (неполио) инфекции в Российской Федерации, в долях от заболеваемости за год (2013–2018 гг.), в лучах линейно-круговой диаграммы месяцы с января (1) по декабрь (12)

При сравнении показателей заболеваемости всего временного ряда (2006–2019 гг.) и временного ряда 2010–2019 гг. среднегодовой темп прироста (4,4 % против 17,7 %) и угол наклона линейного тренда (34 ° против 50 ° ) имели статистически значимые отличия ( х ² = 11,08; d.f. = 1; p = 0,0009).

Для изучения периодичности во временном ряду заболеваемости ЭВнИ был использован спектральный анализ Фурье с целью определения корреляции функций синусов и косинусов различной частоты с наблюдаемыми данными (рис. 2).

При изучении многолетнего уровня заболеваемости ЭВнИ (2006–2019 гг.) спектральный анализ Фурье выявил четырехлетнюю периодичность. Локальные минимумы следовали после локальных максимумов также с периодичностью в четыре года.

Заболеваемость ЭВнИ характеризовалась выраженной летне-осенней сезонностью (рис. 3).

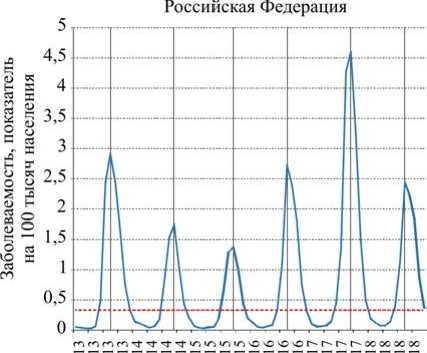
Месяцы наблюдения (2013-2018 гг.)

--- Заболеваемость ЭВнИ

........ Медиана заболеваемости ЭВнИ

Рис. 4. Годовая динамика заболеваемости энтеровирусной (неполио) инфекцией в Российской Федерации (2013–2018 гг.), случаев на 100 тысяч населения

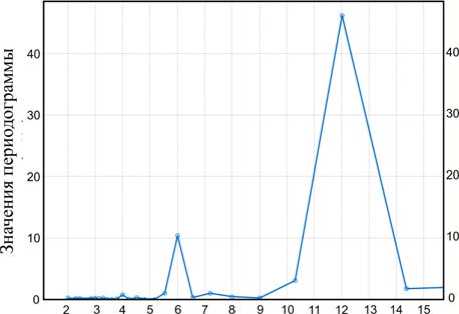
Период

Рис. 5. Периодограмма помесячной заболеваемости энтеровирусной (неполио) инфекцией в Российской Федерации (2013–2018 гг.): ось OX – периодичность в годах, ось OY – дисперсия данных на соответствующем периоде

Сезонный подъем заболеваемости ежегодно начинался в июле и заканчивался в ноябре, максимум заболеваемости приходился на август и сентябрь (рис. 4). По среднемноголетним данным на сезонный период заболеваемости ЭВнИ (с июля по ноябрь) приходилось 89,5 % заболевших. Удельный вес заболевших за счет влияния сезонных факторов составил 82,0 %.

Спектральный одномерный анализ Фурье временного ряда месячной заболеваемости выявил ярко выраженную 12-месячную периодичность, что свидетельствовало об отсутствии значительных сдвигов начала и окончания эпидемического подъема (рис. 5).

Сезонная составляющая при классической сезонной декомпозиции данного временного ряда (метод Census I) как при аддитивной, так и при мультипликативной моделях демонстрировала ежегодное максималь-

Таблица 3

Сезонные составляющие ежемесячной заболеваемости энтеровирусной (неполио) инфекцией в Российской Федерации (2013–2018 гг.)

Месяц Сезонная составляющая при мультипликативной модели Сезонная составляющая при аддитивной модели Январь 14,5887 –0,708005977 Февраль 8,8814 –0,73590166 Март 6,4100 –0,746689643 Апрель 7,4807 –0,74039556 Май 11,0901 –0,708328827 Июнь 39,1541 –0,498259943 Июль 143,0773 0,413094759 Август 307,2373 1,71443414 Сентябрь 314,4177 1,68170537 Октябрь 216,7095 0,913272973 Ноябрь 92,1674 –0,05959021 Декабрь 38,7857 –0,525335427 ное влияние сезонного фактора на увеличение показателя в июле, августе, сентябре и октябре (табл. 3).

Найденная периодичность оказалась универсальной по отношению ко всему временному ряду, однако при этом каждый год может иметь индивидуальные особенности начала и окончания эпидемического подъема. Для расчета эпидемических порогов для наблюдаемых периодов были использованы ретроспективные значения вне сезонных эпидемических подъемов заболеваемости. Был выбран способ первичного разделения временных периодов по уровню заболеваемости на круглогодичную заболеваемость и сезонные подъемы по медиане всего массива данных. Данный способ широко распространен в практике анализа временных рядов заболеваемости, проводимого Всемирной организацией здравоохранения, поскольку на медиану, в отличие от других средних величин (среднее арифметическое, среднее геометрическое, среднее гармоническое), не оказывает существенного влияния пик уровня заболеваемости.

Произведя расчет верхних толерантных пределов (табл. 4), установили, что величина эпидемического порога с января по май не превышала 0,443 ⁰/ 0000 . Минимальное значение приходилось на апрель - 0,178 ⁰/ 0000 . В июне показатель был максимальным и составил 0,575 ⁰/ 0000 . Особо отметим, что уровень заболеваемости в ноябре превышал не только общее медианное значение, но и в четырех случаях из шести – максимальный эпидемический порог. В связи с этим был сделан вывод о включении ноября в число месяцев сезонного подъема заболеваемости, несмотря на низкие значения его сезонной составляющей.

Таблица 4

Эпидемические пороги заболеваемости энтеровирусной (неполио) инфекцией, рассчитанные по данным ежемесячной заболеваемости в Российской Федерации в 2013–2018 гг., случаев на 100 тысяч населения

Месяц	2013	2014	2015	2016	2017	2018	Среднемесячный уровень	Верхний толерантный предел	Медиана
Январь	0,052	0,138	0,074	0,117	0,101	0,192	0,112	–	0,10937
Февраль	0,038	0,106	0,037	0,049	0,057	0,126	0,069	–	0,05281
Март	0,03	0,077	0,029	0,042	0,059	0,075	0,052	–	0,05076
Апрель	0,031	0,041	0,045	0,058	0,076	0,075	0,054	–	0,052
Май	0,064	0,061	0,049	0,083	0,144	0,132	0,089	–	0,074
Июнь	0,476	0,173	0,192	0,327	0,443	0,394	0,334	–	0,36
Июль	2,426	0,808	0,637	1,1	1,356	1,118	1,241	–	1,109
Август	2,913	1,528	1,288	2,722	4,271	2,444	2,528	–	2,583
Сентябрь	2,449	1,744	1,374	2,4	4,598	2,222	2,465	–	2,311
Октябрь	1,654	1,036	1,001	1,805	3,231	1,834	1,76	–	1,729
Ноябрь	0,757	0,432	0,443	0,753	1,481	0,862	0,788	–	0,755
Декабрь	0,33	0,21	0,193	0,312	0,498	0,361	0,317	–	0,321
Помесячная заболеваемость с порогом по медиане всего массива данных							Медиана (все месяцы, 2013–2018)		0,328
Январь	0,052	0,138	0,074	0,117	0,101	0,192	–	0,443	–
Февраль	0,038	0,106	0,037	0,049	0,057	0,126	–	0,322	–
Март	0,03	0,077	0,029	0,042	0,059	0,075	–	0,195	–
Апрель	0,031	0,041	0,045	0,058	0,076	0,075	–	0,178	–
Май	0,064	0,061	0,049	0,083	0,144	0,132	–	0,355	–
Июнь	э	0,173	0,192	0,327	э	э	–	0,575	–
Июль	э	э	э	э	э	э	–	–	–
Август	э	э	э	э	э	э	–	–	–
Сентябрь	э	э	э	э	э	э	–	–	–
Октябрь	э	э	э	э	э	э	–	–	–
Ноябрь	э	0,432	0,443	э	э	э	–	–	–
Декабрь	э	0,21	0,193	0,312	э	э	–	0,503	–

П р и м е ч а н и е : э – месяц с превышением эпидемического порога.

Выводы. Таким образом, заболеваемость ЭВ-нИ за изучаемый период времени (2006–2019) в РФ характеризовалась двумя разнонаправленными трендами, имела четырехлетнюю периодичность, выраженную летне-осеннюю сезонность (коэффициент сезонности – 82 %). Эпидемический процесс характеризовался неуправляемостью и неблагоприятным прогнозом. Анализ проявлений эпидемического процесса ЭВнИ в многолетней динамике при ее неравномерном распределении по годам установил целесообразность использования математических моделей, аппроксимированных на отдельные временные отрезки. Среднемноголетний уровень заболеваемости за период наблюдения 2010–2019 гг. составил 8,09 °/оооо, среднегодовой темп прироста -17,7 %, угол наклона линейного тренда - 50°. Показатели, характеризующие выраженность тенденции в многолетней динамике заболеваемости, рассчитанные на основе математического моделирования, статистически значимо отличались от таковых, полученных путем расчета средних величин (χ2 = 11,08; d.f. = 1; p = 0,0009).

Повышение качества эпидемиологической диагностики энтеровирусной (неполио) инфекции на популяционном уровне предполагает и обосновывает широкое включение математических моделей в методику эпидемиологического обследования при оценке проявлений эпидемического процесса в многолетней динамике, а также при оценке пространственной характеристики эпидемического процесса.

Финансирование. Работа выполнена в рамках реализации отраслевой научно-исследовательской программы Роспотребнадзора «Проблемно-ориентированные научные исследования в области надзора за инфекционными и паразитарными болезнями на 2016–2020 годы» и предусмотрена п. 1.5.2. (рег. номер в ЕГИСУ НИОКТР АААА-А16-116061710036-0) и п. 3.1.11. (рег. номер в ЕГИСУ НИОКТР АААА-А16-116061710033-9) программы.