О двух характерных примерах в теории автоматического управления

Бугров А. Н., Жарков А. Н., Козлов А. Н. О двух характерных примерах в теории автоматического управления // Системный анализ в науке и образовании: сетевое научное издание. 2022. №4. С.1-7.

URL:

ABOUT TWO CHARACTERISTIC EXAMPLES IN THE THEORY OF AUTOMATIC REGULATION.

Bugrov Alexsej N.1, Zharkov Andrey N.2, Kozlov Oleg A.3

1PhD in Physical and Mathematical Sciences, associate professor;

Dubna State University;

19 Universitetskaya Str., Dubna, Moscow region, 141980, Russia;

2Student;

Dubna State University;

19 Universitetskaya Str., Dubna, Moscow region, 141980, Russia;

3Student;

Dubna State University;

19 Universitetskaya Str., Dubna, Moscow region, 141980, Russia;

Педагогическая практика фиксирует значительные трудности, которые испытывают современные студенты, начинающие изучать такие насыщенные математикой предметы, как теория автоматического управления. И хотя этот предмет не освоить без знания ряда разделов высшей математики: интегрального и дифференциального исчислений, высшей алгебры, а также механики, электротехники и др., не стоит сбрасывать со счетов и стремление педагогов высшего образования сделать это вхождение менее напряженным и более комфортным, а, следовательно, более продуктивным.

Одним из таких приемов, значительно упрощающих трудности начального освоения предмета студентами, может служить «задачный подход», широко используемый на кафедре САУ Института САУ Университета «Дубна». Подход заключается в том, что первоначальное ознакомление студентов с учебной дисциплиной осуществляется на характерных примерах-задачах, демонстрирующих основную проблематику и инструментарий дисциплины, которую надо освоить.

В работе приводятся два характерных примера, которые могут быть использованы в качестве тех, на которых можно демонстрировать проблематику и инструментарий теории автоматического управления (регулирования). Сравнивается степень сложности этих примеров для усвоения, предпочтение отдается примеру, описывающему функционирование поплавковой камеры карбюратора.

Специалистами по автоматическому управлению считается, что первым автоматическим регулятором промышленного назначения является центробежный регулятор для стабилизации скорости вращения рабочего вала паровой машины, разработанный предположительно в 1784 году шотландским инженером Джеймсом Уаттом. На первенство в нише промышленных регуляторов мог бы претендовать и поплавковый регулятор уровня воды в паровом котле, изобретенный Иваном Ползуновым в 1765 году, и уже эксплуатируемый к 1784 году на Колыванских Заводах Алтая. Поплавок “измерял” уровень жидкости и посредством рычагов воздействовал на клапан, регулирующий подачу воды в паровой котел. Однако, если центробежный регулятор Уатта оказывал регулирующее воздействие на выход объекта управления – скорость вращения вала парового двигателя (паровой машины), то регулятор уровня Ползунова регулировал внутренний показатель состояния паровой машины – уровень жидкости в паровом котле.

Для начального ознакомления студентов, изучающих теорию автоматического регулирования (управления), можно использовать как первый – центробежный регулятор

Уатта, так и второй -регулятор уровня жидкости Ползунова. Однако, на наш взгляд, целесообразно начинать с примера, обладающего большей простотой и наглядностью, а значит и большей доступностью для восприятия студентами и, следовательно, большей педагогической ценностью. Сравнивая сложность описания и, следовательно, сложность для усвоения представленных примеров студентами, на наш взгляд, рационально обратиться к третьему характерному примеру устройства автоматического регулирования -поплавковой камере карбюратора, выполняющую ту же задачу, что и регулятор уровня жидкости Ползунова, широко применяемую в карбюраторах двигателей внутреннего сгорания. А именно регулирование уровня жидкости в сосуде, в данном случае топлива в поплавковой камере карбюратора.

Карбюратор – устройство для подготовки топливно-воздушной смеси для двигателя внутреннего сгорания, был изобретен в 1814 году П. Кристофоресом. Патент на карбюратор был получен У. Барт-нером в 1838 году. Один из первых автомобилей с карбюраторным двигателем был построен макленбургским механиком З. Маркусом в 1864 году.

К настоящему времени современный карбюратор – достаточно сложная система, выполняющая ряд функций при функционировании двигателя внутреннего сгорания. Однако его непременным компонентом является поплавковая камера, служащая для регулировки уровня топлива, снабженная поплавком и запорной иглой, весьма схематично изображенная на рис. 1.

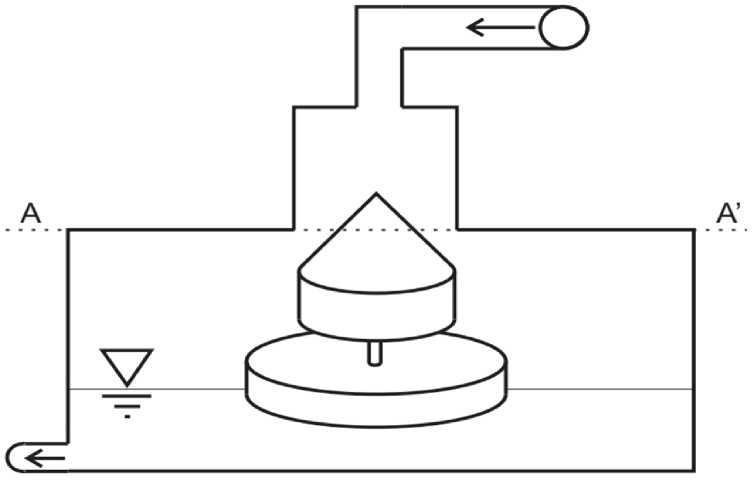
Рис. 1. Схематичное представление поплавковой камеры карбюратора

Принцип работы поплавковой камеры карбюратора достаточно прост – при повышении уровня бензина поплавок всплывает и посредством запорной иглы перекрывает площадь верхнего входного отверстия, тем самым препятствует дальнейшему повышению уровня топлива. При снижении уровня происходит обратное действие – верхнее входное отверстие приоткрывается и увеличивается приток бензина в поплавковую камеру.

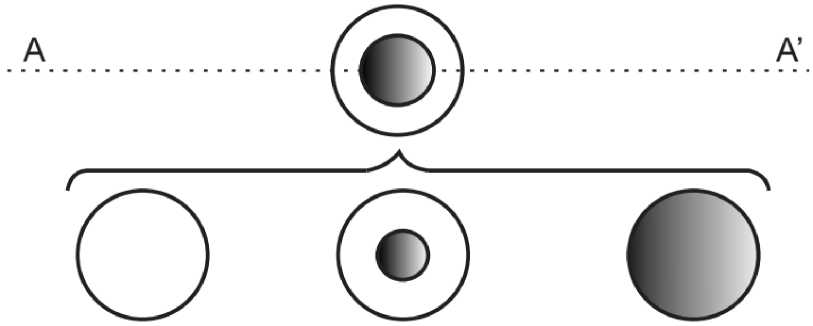
Рис. 2. Степень перекрытия запорной иглой входного отверстия поплавковой камеры. Правое положение -отверстие полностью перекрыто, среднее -частично, левое - полностью открыто

На рисунке показана степень перекрытия запорной иглой входного отверстия поплавковой камеры карбюратора в зависимости от уровня топлива а, следовательно, и положения поплавка. Такое поведение поплавка и запорной иглы приводит к появлению контура отрицательной обратной связи в системе и наделяет эту систему (емкость поплавковой камеры – поплавок – запорная игла – верхнее отверстие) регуляторными свойствами.

Для построения математической модели поведения уровня топлива в поплавковой камере карбюратора изобразим процессы, в результате которых уровень топлива изменяется за небольшой промежуток времени Δ t :

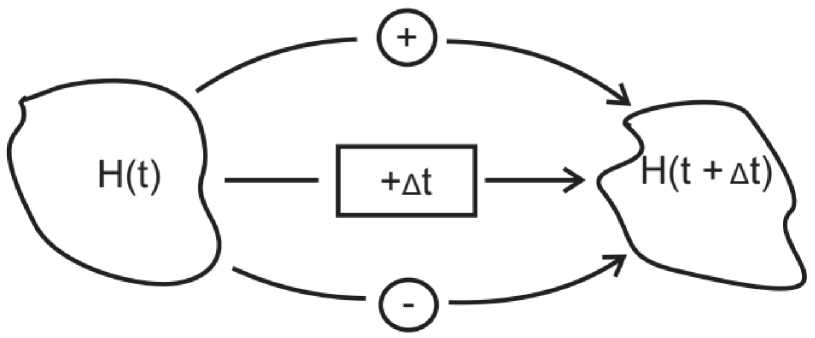
Рис. 3. Условное изображение процессов, изменяющих уровень топлива в поплавковой камере карбюратора за небольшой промежуток времени Δt. Знаком «+» помечено поступление топлива от бензонасоса через запорное устройство: «входное отверстие» плюс «запорная игла», в результате чего уровень топлива в поплавковой камере повышается. Знаком «–» помечено поступление топлива из поплавковой камеры в двигатель внутреннего сгорания, в результате чего уровень в поплавковой камере понижается

Для формулировки математической модели записываем баланс массы топлива на промежутке времени от t до t + Δ t , где Δ t << 1 достаточно мало:

Масса топлива в момент времени t +Δ t - Масса топлива в момент времени t = Поступление топлива за Δ t из бензобака - Расход топлива за Δ t в двигатель внутреннего сгорания (1) и выразить эти величины через параметры поплавковой камеры и характеристики процессов поступления и расхода топлива. Баланс массы топлива в левой части предыдущего равенства на промежутке времени от t до t + Δ t выражается достаточно просто, и он равен величине:

ρS дна H(t+Δt) - ρS дна H(t),                                      (2)

где ρ – плотность топлива, S дна – площадь дна поплавковой камеры, H ( t ) – уровень бензина в момент времени t. Поступление топлива из бензобака через верхнее отверстие может быть описано с помощью геометрических характеристик запорной иглы, форма которой принимается в виде конуса и величины уровня бензина либо в терминах рабочего интервала изменения уровня бензина H min < H(t) < H max :

πR 0 ²(1 - ((H- H min )/( H max – H min ))²)uΔtρ,                              (3)

где R 0 – радиус верхнего головного отверстия, u – скорость (расход) поступления топлива из бензобака, принимаемая постоянной величиной и определяемой производительностью бензонасоса автомобиля.

Расход топлива за время Δt, поступающего в двигатель внутреннего сгорания, определяется формулой Торричелли:

Κj2gH(€)S_OTBMp,                                (4)

где g – ускорение свободного падения, Κ – коэффициент, характеризующий внутреннее трение топлива, , S отв – площадь придонного отверстия поплавковой камеры, ρ – плотность топлива.

Собирая все слагаемые описывающие баланс и переходя к пределу при A t стремящемуся к нулю, получаем уравнение, описывающее поведение уровня бензина:

S дна^ к -К: -гН ■ J--,- nR o ²(1-((H- H mn )/(H max - H min ))²)u

при соответствующем начальном значении уровня топлива:

H (0) =H ₃                                       (6)

Идентификация предлагаемой модели состоит в задании конкретных числовых параметров рабочего диапазона изменения уровня бензина H min , H max , геометрических характеристик поплавковой камеры, скорости поступления топлива из бензобака- напора, создаваемого бензонасосом. Геометрические характеристики поплавковой камеры задаются из приблизительных представлений о размерах поплавковой камеры. Основное требование к задаваемым параметрам заключается в том, чтобы значение правой части дифференциального уравнения, описывающего поведение уровня f(H) при минимальном уровне бензина H min было положительным, а при максимальном уровне H max было отрицательным. Последнее условие очевидно выполняется, так как при верхнем значении уровня топлива из рабочего диапазона верхнее отверстие закрыто и топливо не поступает в поплавковую камеру. Интерпретация этих условий очевидна: при минимальном значении уровня бензина и близких к нему значениях поплавковая камера должна заполняться, а при максимальном значении уровня бензина должна опорожняться. В силу непрерывности правой части уравнения модели (4) будет существовать такое значение уровня бензина H min <  H s <  H max при котором правая часть f(H s ) будет равна нулю. Эту величину достаточно просто вычислить приближенно при заданных параметрах модели с помощью известных методов определения нулей непрерывной функции, например методом деления отрезка пополам. Найденное значение уровня бензина H s соответствует такому состоянию уровня бензина, когда количество топлива поступающего в камеру двигателя внутреннего сгорания будет равно количеству топлива, поступающего из бензобака.

Таким образом рабочий интервал [ H min , H max ] разбивается величиной H s на два подинтервала: на первом подинтервале [ H min , H s ] в силу уравнения динамики уровня топлива имеем -7     а на втором

Нетрудно увидеть, что это обстоятельство обеспечивает устойчивость стационарного решения H(t)=H s .

После формулировки нелинейной задачи, описывающей поведение уровня топлива в поплавковой камере, можно осуществить расчет этого поведения, например процесс заполнения камеры бензином. Расчет можно осуществить, например, с помощью метода Рунге – Кутты 4 порядка точности. Повышенная точность определяется нелинейностью задачи. Результаты расчета динамики уровня бензина при заданных параметрах, описывающих геометрию поплавковой камеры карбюратора и скорость поступления бензина из бензобака приводятся на рис. 4.

Рис. 4. Динамика уровня бензина в поплавковой камере карбюратора при заполнении топливом

Из результатов расчета видно, что уровень бензина не превышает стационарного значения H s в случае исправной поплавковой камеры карбюратора. Поэтому рабочий интервал [ H min , H max ] измене-

Сетевое научное издание «Системный анализ в науке и образовании» Выпуск №4, 2022 год ния уровня следует заменить на диапазон [ H min , H s ]. Ситуация H(t) > H_s возможна лишь в случае неисправности механизмов поплавковой камеры и носит название «перелив» и свидетельствует о неисправности карбюратора.

Представляет интерес изучение реакции уровня бензина на резкое нажатие водителем дроссельной заслонки - педали газа, которое приводит к резкому уменьшению уровня с последующим его восстановлением. Это воздействие можно описать добавлением к уравнению в правой части дополнительного слагаемого – иглообразной функции* (термин, используемый в теории импульсных функций), являющейся моделью обобщенной функции Дирака:

S дна Κ j2gH (t)5_BT1 + πR 0 ²(1-((H- H min )/( H max - H min ))²)u – сδ(t*),¹ (7)

где с – величина изменения уровня топлива при резком нажатии водителем педали газа, не превышающая уровень топлива H s , t * – момент времени нажатия на педаль газа. Тогда график изменения уровня бензина примет вид:

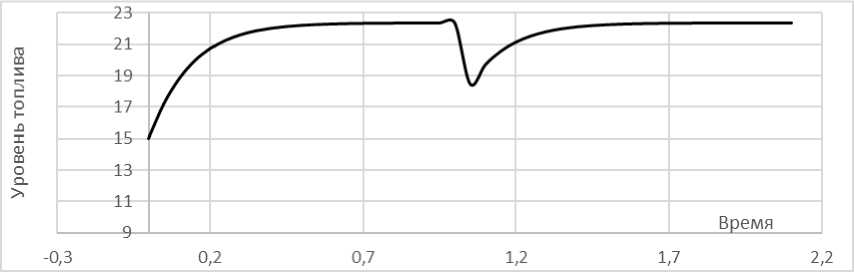
Рис. 5. Динамика уровня бензина в поплавковой камере карбюратора при резком нажатии водителем дроссельной заслонки - педали газа, который демонстрирует работу карбюратора при резком нажатии водителем дроссельной заслонки - педали газа, которое приводит к резкому уменьшению уровня с последующим его восстановлением

Линеаризация уравнения движения поплавковой камеры в окрестности стационарной точки H s приводит к хорошо известному уравнению динамического звена первого порядка, устойчивого при отрицательном значении производной правой части по переменной – уровень топлива при H=H s .

Поплавковая камера карбюратора, её описание функционирования представляет, на наш взгляд, удобный пример для начального освоения предметной области автоматического регулирования (управления), в отличие от более сложного примера – паровой машины с центробежным регулятором Уатта. Действительно, математическое описание её функционирования приводит к системе обыкновенных дифференциальных уравнений:

d2»       »   .              ma .

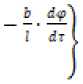
m —7 = nuo ■ sin

• cos cp --— • sin

/57= ki-cosp -F

Относительно переменных:

– угла отклонения тяг грузиков центробежного регулятора от вертикали, масса которых равна m , – угловой частоты рабочего вала паровой машины. В (8) n – передаточное число шестереночной передачи, g – ускорение свободного падения, b – коэффициент трения подвижной втулки регулятора по его валу, k – некоторый коэффициент пропорциональности, J – момент инерции маховика, F – величина, определяемая нагрузкой. По поводу формулировки системы обыкновенных дифференциальных уравнений (8) [1].

Система обыкновенных дифференциальных уравнений путем введения нового переменного – угловой скорости вращения вала центробежного регулятора, приводится к нормальной форме:

dr *

dTp          ₂   .                  g . b

— = n • to ■ sin ф ■ COS ф ---sin ф — — • w dr                              i           mi '

du ki             F

— = — cos ф — —.

J

dr

и подвергается известной процедуре: отыскивается стационарное решение системы P = У , = 0, Ш = Ш и далее устанавливаются условия устойчивости этого стационарного решения. Именно этот подход был реализован И. А. Вышнеградским. Результатом его исследования послужили знаменитые тезисы и диаграммы, которыми до сих пор пользуются проектировщики паровых машин [2]. И. А. Вышнеградским были найдены достаточные условия устойчивости стационарного решения в линейном приближении. Эти исследования приводят к изучению устойчивости характеристического полинома 3 степени, стандартным образом, формулируемым по линейному приближению системы (9).

Все это налагает определенные требования на математическую подготовку обучающегося по сравнению с определением устойчивости стационарного решения Hs поплавковой камеры карбюратора. Однако при более углубленном изучении вопросов функционирования автоматических устройств регулирования центробежный регулятор Уатта становится незаменимым в качестве иллюстрации потери устойчивости при изменении (либо неправильном выборе параметров при проектировании) параметров паровой машины. В математике, а точнее в теории обыкновенных дифференциальных уравнений, это явление потери устойчивости решения при изменении параметров устройства носит название «параметрической бифуркации». Последняя связывается с именами А. Пуанкаре (1854-1912) и А. А. Андронова (1901–1952). Для иллюстрации потери устойчивости путем бифуркации при изменении значений параметров в теории обыкновенных дифференциальных уравнений принято рассматривать пример однопараметрического семейства векторных полей на плоскости, записываемой в комплексной форме:

— = zUw + E + CZZ) dt                            ^,

где z = x + iy комплексная координата на плоскости R² , рассматриваемой как плоскость комплексной переменной z , Ci) И c – вещественные ненулевые постоянные, E – вещественный параметр [3]. Наша практика показывает, что подобный пример иллюстрации явления бифуркации достаточно сложно воспринимается студентами инженерных специальностей с относительно скромной математической подготовкой и, соответственно, математической практикой по сравнению со студентами – математиками, прикладными математиками.

Более эффективным, на наш взгляд, является использование центробежного регулятора Уатта в качестве компьютерного тренажера. А именно, меняя параметры паровой машины и регулятора-массу грузиков, коэффициенты трения, угловую скорость паровой машины и т.п. мы можем добиваться как устойчивого стационарного режима, так и потери его устойчивости. Потеря устойчивости может проходить как мягко с появлением слабой вибрации - автоколебаний, так и жестко – паровая машина «идет в разнос». В этом случае в системе в результате срыва стационарного равновесия и жесткой потери устойчивости реализуется такой режим, который не является автоколебательным. Подобный компьютерный тренажер для освоения работы паровой машины с центробежным регулятором Уатта и визуализации динамических портретов режимов работы в том числе и их бифуркаций в системе паровая машина- центробежный регулятор был реализован в [4] под руководством одного из соавторов данной работы.