О единственности обобщенных решений систем дифференциальных уравнений c постоянными коэффициентами

Произвольный линейный дифференциальный оператор с постоянными коэффициентами в R ⁿ будем записывать в виде

P ( D ) = X p j D^{j ,} P j e C,

JJ sm dlj\ где D = ij^—a,j=(ji’^’j«) ,1A=j+„+ j«,i = 'A-1, о j1 „.a

51         5n a § = (^1,„, ^n) — некоторая фиксированная система координат в Rn.

Пусть z = ( z ₁, „ , z_n ) — точка n -мерного комплексного пространства

Сn.

Многочлен p(z) = ЕPjZJ,zJ = zJ „zJnn называется характеристическим по отношению к оператору P (D). Алгебраическое многообразие в N с Cn, образованное корнями многочлена p (z), также называется ха- рактеристическим.

Рассмотрим произвольную однородную систему линейных дифференциальных уравнений с постоянными коэффициентами.

P ii ( D ) u i +„ + P is ( D ) U s = 0,

Pti (D) Ui + „ + Pts (D) Us = 0, где Pij (D), i = 1, t, j = 1,5 — произвольные линейные дифференциальные операторы с постоянными коэффициентами, а числа t и s — произвольны.

Такую систему мы будем записывать в матричной форме:

P ( D ) u = 0,                            (2)

где u = (u₁, „ ,u_s) — неизвестная вектор-функция.

Рассмотрим Жевреевские пространства финитных функций и сопряженные пространства. Для любого B >  0 и в >  1 через Dp^,в обозначим пространство бесконечно дифференцируемых функций в Rⁿ с носителями, принадлежащими компакту F, и конечной нормой вида:

,,       max|^D^ ⁽ ; )|

^{11 и} = p Bj ■

'

Пусть (D1 ) — сопряженное пространство, норму в этом пространст ве мы будем обозначать через ||-|j^B

Рассмотрим класс основных функций D ^ = I B > 0 D ^*B .

Введем в нем счетное число норм

И Г .B = 1 ■ k = 1.2. ^

Обозначим через UFβ пространство линейных непрерывных функционалов над пространством DFβ .

По свойству линейного непрерывного функционала каждый элемент Up непрерывен по некоторой форме ||-|| ^e ' B .

Определение 1 . В [1] характеристическим множеством системы (1) и оператора P ( D ) называется алгебраическое многообразие

N = { z е C n ;rang p ( z ) <  s } .

где p ( z ) — матрица. полученная заменой операторов P ij ( D ) многочленами py ( z ) .

Пусть N — некоторое алгебраическое многообразие. Пространство Cⁿ вложим в C^{n + 1} с помощью отображения z ^ ( 1.z ) . Пусть H(N)— совокупность всех однородных многочленов в C^{n + 1}. отображающихся в нуль наN .

Определение 2 . Любая точка вида ( 0.z ) . z e Cⁿ. в которой обращаются в нуль все многочлены из H(N), называется несобственной точкой многообразия N .

Пусть N — характеристическое множество системы (1). Множество прямых в Cⁿ , отвечающих несобственным точкам алгебраического многообразия N. обозначим через N ' .

Множество N ' есть алгебраический конус. В случае s = t = 1 система (1) сводится к уравнению. В этом случае N ' есть множество корней многочлена p m ( z ) .

Находятся достаточные условия для единственности продолжения обобщенных решений системы (1), определенных в окрестности объеди нения граней πk в окрестность параллелепипеда π в специальном k=1

классе обобщенных функций бесконечного порядка. Обозначим через N характеристическое множество оператора P ( D ) . а через N ' — конус. образованный комплексными прямыми, отвечающими несобственным точкам алгебраического многообразия N .

Постановка задачи

В этой статье изучается следующая задача: при каких условиях всякое обобщенное решение бесконечного порядка системы уравнений в частных производных с постоянными коэффициентами, определенное в окрестности трех соседних граней параллелепипеда в R ⁿ , может быть единственным образом продолжено в некоторую его окрестность. Эта задача является аналогом классической задачи Дарбу — Гурса — Бодо для обобщенных решений: вместо значений решения и его производных на гранях (которые, вообще говоря, не определены, если плоскости этих граней характеристические) решение задается сразу в некоторой его окрестности.

Важные теоремы

Теорема 1. N' с |J_k{ z e C n ;z_k = 0} ,тогда V в >  1 и для любой окрестности L компакта ^Jn k существует окрестность L ' компакта п, такая, k = 1

что всякая обобщенная функция u e|^ U_k . J , являющаяся решением системы (1) на L ' и равная нулю на L, будет равна нулю на L ' .

Доказательство. Пусть u — произвольное решение системы (1), при надлежащее пространству ГUва J  при некотором а, u | а = 0.

^П                                          I U n k I

V k = 1 )

l

Введем функционал ц = ^ d^v ( z,D_z ) ц^х , тогда в силу теоремы ([1],

Z = 0

гл. VI, §4, теор. 2) ( u,ф ) = ( ц,ф * ) , V ф g^- J s .

Обозначим для любого число D > 0 и целого m > 0 через Sβm,,DF про- странство бесконечно дифференцируемых функций ψ в Cn, для которых

Г 1 )

D j V ( x,y ) < cJ F ( y ) exp I - D|z| в I при любом j, |j| <  m.

Рассмотрим пространство   S | ^,D = Qs mD .

m > 0

В пространстве SβF,D введем систему норм

Iv ( x,y ⁾ mD_F| =

l_ i¹ | D ^jy| exp I D|z| в

max sup

J F ( У ) j <  m z

, m=0,1,2,…

'

Через ( S p, ) обозначим пространство непрерывных линейных функ

'

ционалов на Sp, , а через (Sp, ) обозначим множество функционалов f e

( S F,D )

s _t

, для которых ( f,Pv ) = 0 при любом v е pPD J , где е >  0.

' ^s

Норму для элементов пространства ( s F ^,d )

, сопряженную с нормой

| mD в пространстве |^S F ^,D J , обозначим через |||-|| p^

.

Символом * будем обозначать операцию инволюции, определенную для функций, заданных в С^п, которые сопоставляют функции ф ( z ) функцию ф * ( z ) = ф ( z ) . '

Покажем, что функционал ц e ( s F _a - 1 ) .

Так как d^X ( z,D_z ) , X = 0,1 в [l] (гл. 4, §4, п. l нормальные операторы Паламодова — Нетер) — матричные дифференциальные операторы с полиномиальными коэффициентами, то, обозначая наивысший порядок производной в d^X ( z,D_z ) , X = 0,l через m 1

V v e |^S F ^{,D + e} J , мы получим оценку

|| d^{X (} z,Dz ) ^V(^D< c(X)| ^^ , ^X = ^0,1 .

В силу этой оценки V v e ^ S n a D ^{+ e} J имеем

KJ(dX*(z,Dz) ^v )| = rj k ,dx (z,Dz) v ^eli ЮdX (z,Dz) C c2 IMP У1 схi IMP" < c3IM в,В IIvlP"

2 11 lln^a Z—iX =0 (X) 'llm_l,n^a1       3 11 lln^a ll'llm_l,n^al

.

5     5

Здесь D — вектор с компонентами —,...,--- , z                                     Sz1     6zn p' — матрица, транспонированная с матрицей p.

В силу (3) V y е |^ S n a D i ⁺ 2 ^e J имеем

l

( P,P» ) = У ( р^Х,d^Z ( ^z,Dz ) P ' W ) = ⁰ . л = 0

''

Следовательно, р е ( s n a D ^Е ) ,откуда следует, что р е^^- ) .

s

D^e_{a - 1} I ,i = 1,2,3, имеем ⁿ i J

( u, ф ) = ( р,ф * ) = 0, где ф * е ( D^ ) ,i = 1,2,3. В силу леммы 3.1.10 в [4] функционал μ обращается в нуль на целых функциях пространства

S

SL 2 I ,i = 1,2,3. TT.         I

Применяя аналог первой теоремы Мальгранжа ([2; 5]) к функционалу μ и каждому из выпуклых компактов π₁,π₂,π₃, получим *

р-z

41 dzs j

μis,j , где μis,j

е

| и i * j,i,j = 1,2,3. P

Обозначим x S ^,j = P S - P S , так как

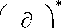
kdZs J

x S ^,j = ^{0 на}

функциях

пространства

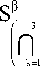
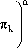
и χis,j

е

Sβ

n

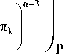
, то, применяя к функцио-

налам χis,j аналог второй теоремы Мальгранжа в ([3; 5]), мы получим, что существуют функционалы

X s,t ^е

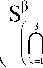
a - 4

такие, что

X ij = У —

Лs  ^ az

t = 1 k ^zt J

X s,t , причем X s,t =- X t,s .

В дальнейшем будем использовать функции h0,h1,h2,h3 построенные в лемме 3.1.2 [4].

Обозначим h i х st через х St , i = 0,1,2,3- В силу леммы 3.1.7 в [4],

s

V у G

S

β

а — 4

имеем

Ink k=1

^(ho X s,t ,У) = ( х s,t^,h0 у ) = 0.

Поэтому на функциях пространства

s

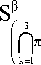
X s,t = ( h o + h l + h 2 + h 3 ) X s,t = ^ho X s,t + ^h1 X s,t + h 2 X s,t + h 3 X s,t =

= xs,t + х 2,t + х 3,t, причем в силу леммы 3.1.6 [4]

х s,t ^c ( ^{S e} 4 )_p i * ^j,i,j = ^1,2,3 .

Введем функционалы Ц s’j = Цу¹ + ^

d d z_t

*

χ s ^, ,t .

Очевидно,   Ц s ^,j

"К 4 )p.

Покажем на

функциях пространства

s

S^e 3      , a - 4

I n n k l

-1

' H s

-2

H s .

Учитывая, что на функциях этого пространства х⁰_t = 0, будем иметь

~ 1     ~

H s ^- H

2 s

= ц

s

—

μ s ²

*

I х s ² ,t

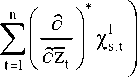
= х;

1,2

—

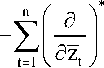
= х

1,2 s

^— х S ^,2

= 0.

Аналогично находится, что s цs = цs , где i Ф j,i,j = 1,2,3 на пространстве

β

3    \а — 4

| П п к |

.

Так как X s,t = - X t,s , то

μ i _s ,j

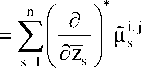
Покажем, что У ф е [d^ j ] , ( й,ф * ) = 0.

Для этого V y е [ s ^- । ] построим функционал ( ^й s , у ) = ( M- S , h i У ) + ( ^й 2 , ^h2 У ) + ( й 3Л У ) .

I ^s

S *, у—4    . Так

I П ^п I

V k = 1 )

Покажем, что йs = ЙS,j на функциях пространства как на функциях этого пространства    йS = Й2 и    h0ЙS'1 = 0, то

( ^Йs ,У ) =

= ( J% S , h i У ) + ( ^й 2 , ^h2 У ) + ( ^{й 3}Л У ) = ( ^й1,2 , ( ^h0 + h i + ^h2 + ^h3 ) У ) = ( ^й s j ,У ) .

Откуда следует, что V y е

й-Е

д dz.

*

д д/

*

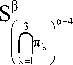
, имеем представление

йs . Так как пространство

β

3    \а-4

l i n k I

s

плотно в пространстве [ s ¹^ . ]

и так как

йs е [s1^—. ] , то в силу линейности и непрерывности функционалов йs получим представление й = ^

д ^{d z}s ,

*

йs на функциях пространства

Е^ L

В силу леммы 3.1.9. в [4], ( D ^ ) с S F , если ф е [d^ s ] т.е.

supp   ф с л"' 5 есть компакт, то ее преобразование Фурье продолжа ется в Сn как целая аналитическая функция

ф * g [^- 4 J , в силу этого V p g ^ D^ J будем иметь

*

I И s

*                д ~*

,ф =У иs,^• ф 1 = 0 .J Т=11 5zs    )

Теорема доказана.

Заключение

Найдены достаточные условия на множество комплексных прямых, отвечающих несобственным точкам алгебраического многообразия, обеспечивающие единственность продолжения обобщенных решений дифференциальных уравнений в частных производных с постоянными коэффициентами с окрестности трех соседних граней параллелепипеда в R ⁿ , в некоторую его окрестность в классе обобщенных функций бесконечного порядка.