О единственности решений уравнения Бельтрами с заданной вещественной частью на границе

DOI:

,

1.    Предварительные факты

Основная цель данной работы посвящена установлению одной специальной теоремы единственности для уравнения Бельтрами (см. раздел 3), которое тесно связано с двумерными квазиконформными отображениями и теорией обобщенных аналитиче- ских функций [2]. Однако особенностью основного результата нашей работы является то, что получен он был на основе (двумерного) частного случая результата работы [4], касающегося асимптотического поведения решений эллиптического уравнения вида

Ди + с(х)и = 0,

заданного на некомпактном римановом многообразии М , имеющем конец A С М специального вида. Эллиптические уравнения на некомпактных римановых многообразиях вызывали и вызывают интерес многих исследователей (см., например, [3; 5; 7–12; 17] и библиографию в них).

Приведем необходимый нам вышеупомянутый результат работы [4] в удобной для нас формулировке.

Пусть М — некомпактное многообразие класса С “ , снабженное римановой метрикой д класса С “ ; dim М = N >  2. Допускается, что дМ = 0 и М не предполагается полным. Обозначим Л — оператор Лапласа — Бельтрами в метрике д.

Пусть A С М — некоторое множество. Следуя [17, с. 212] (см. также [5]) будем называть A концом многообразия, если выполнены следующие условия

• 1)    замыкание [A ] в топологии М не является компактным;

• 2)    д A — компакт.

Пусть F (х) : A ^ R — некоторая функция и А произвольное вещественное число или один из символов то , + то , —то . В дальнейшем будем говорить, что F(х) стремится к А на конце A или имеет предел А, если для любой последовательности точек х _п G A не имеющей точек накопления в М выполнено F(х _п ) ^ А при п ^ то . Записываем этот факт следующим образом: lim F(х) = А.

Пусть A С М конец многообразия М (см. [5]). Будем предполагать, что замыкание [A] изометрично многообразию с краем R+ х S, где R+ = [р0, +то), S — компактное риманово многообразие без края (dimS = N — 1), на котором задана метрика dl2 = h2(p)dp2 + q2(p)d02.                                 (2)

Здесь h(p),q(p) — положительные гладкие функции, заданные на R + , а

N -1

d02 = ^ Wij (0)d0id0j i,j=1

риманова метрика класса С “ , заданная на S. Здесь 0 G S, а 0 _i — обозначают локальные координаты на S . Через Л ₀ будем обозначать оператор Лапласа — Бельтрами в метрике d0 ² .

Пусть на М определено дифференциальное уравнение (1). Решения уравнения (1) понимаются в классическом смысле, то есть это функции и = f (х) G С “ ( М ), дающие при подстановке в это уравнение верное равенство.

В случае с(х) <  0 на М уравнение (1) называется стационарным уравнением Шредингера, а в случае с(х) >  0 — уравнением Гельмгольца.

Предположим, что на конце A в координатах р, 0 функция с(х) имеет вид с(х) = = с(р). Тогда в этих координатах уравнение (1) имеет вид (см. [10])

1 д ² и ,     1                q'    h' ди _:    1

ь ²^ )а р ^{2 +} h 2 (P)[^{( N —} 1) ~q ^— h д р ⁺ q ² (р)^{Л 0 U + с ( р ) и} = ^{0 .          (3)}

Имеет место теорема.

Теорема 1. Пусть задан конец X с М на котором метрика имеет вид (2) . Предположим, что для некоторого а < 2 выполнено

⁺ “ h(s)

J Р о ^ХЕЕ * <                                     ⁽⁴⁾

+м sup (q2V-2)(р) + |c(p>2(V-1)(р))(       (^) ds) < +то.        (5)

p g[ p o , +H^V                              '^V- q^N \s) /

ρ

Тогда, если для некоторых решений f i (p, 0) , f ₂ ( p , 0) уравнения (1) , заданных на М, на конце X имеет место асимптотика

+м

У | f 2 ⁽P, ^{0 )} -Л⁽р, ^{0 ) |}^ = °(/ ^- г^⁵ )

при р ч + то ,

S                                    P то fi(p, 0) = f2(p, 0) на М.

2.    Случай аналитических функций

Всюду далее будем использовать следующие обозначения для комплексных переменных и их вещественной и мнимой частях: z = х + iy, w = и + iv, Z = ^ + in, считая, при этом, что каждая из этих комплексных переменных пробегает область расположенную в отдельном экземпляре комплексной плоскости C.

Далее используем следующие стандартные обозначения:

• 1)    B r (г > 0) — единичный круг в комплексной плоскости c центром в нуле 0 Е C;

• 2)    S _t — окружность в комплексной плоскости радиуса t >  0 с центром в нуле 0 Е C;

• 3)    K t i ,_t 2 — круговое кольцо в комплексной плоскости, ограниченное (концентрическими) окружностями S _t 1 , S _t 2 , причем такими, что 0 < t 1 < t ₂ .

Здесь подразумевается, что B _r , K _t 1 ,_t 2 открытые множества, то есть области.

Доказательству основного результата (теорема 2) предпошлем следующее утверждение.

Лемма 1. Предположим, что в кольце K _R,1 ( 0 < R <  1 ) задана голоморфная функция

w(z). Если lim — /,|Rew(z)||dz | = 0 r^1-0 1 — Г z = гегф

Sr тогда w(z) = ia, где а Е R.

Доказательство. В круге B1 = {(x,y)| х2+y2 < 1} с евклидовой метрикой ds2 = dx2 + + dy2 введем ”обобщенные” полярные координаты (р, 0) (р > 0, 0 Е [0, п)) связанные с координатами x,y формулами х = П arctg р c°s 0, у = П arctg р sin 0, а со стандартными полярными координатами (г, ф) формулами г = П arctg р, ф = 0. В этих координатах евклидова метрика приобретает вид ds2 =      4     [dp2 + (1 + p2)2(arctg p)2d02].

п ² (1 + р ² ) ²

Тем самым круг В 1 можно рассматривать как случай двумерного риманова многообразия (М,д) описанного в разделе 1, а кольцо Кщ как конец на этом многообразии. В координатах (р, 0) ему соответствует область р > tg( П ^). На этом конце метрика (8) имеет вид (2) причем

2           , х 2

^^{( р ) =} _П(1 + _р 2 ) , ^{? ( р )} = П arctg ^Р = ^Г'

Одномерным многообразием S выступает единичная окружность, которую мы отождествляем с промежутком [0, п ). Пусть N = 2, 0 <  а < 2 задано произвольно, с(р) = 0. Прямой проверкой нетрудно убедиться в выполнении условий (4), (5).

Пусть u(z) = и(р, 0) = Rew(z). Эта функция является гармонической в евклидовой метрике. Пусть в теореме 1 f ₂ (р, 0) = м(р, 0), f ₁ (р, 0) = 0. Тогда интеграл из левой части условия (6) равен

У | м(р, 0) | d0 = - У Цг, ф) | гdф = - У | n(z) || dz | ,

г = — arctg р. π

s

S

s _r

Интеграл из правой части (6), с учетом N = 2 и (9) равен

/ тг ds = / ф)

ρ

ρ

ds

(1 + s ² ) arctg s

= ln---П--

2 arctg р

= In —. г

Из (10), (11) имеем

/ h^(s)

J Q⁽s) ^ρ

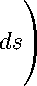
-1

I Цр, 0) | d0 =

s

z1Г / |u(z)||dz| = Ц 1- [ |«(z)||dz|.(12)

ln 1                 г In 1 1 — г r                              r"

sr

Учитывая, что г и р связаны соотношением г = П arctg р, видим что г ^ 1 — 0 О р ^ те . Так как ^- 1 ^ 1 при г ^ 1 — 0, то из (12) и условия леммы (7) вытекает, что r

[ h^(s)

J Q⁽s) ^ρ

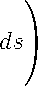
-1

У Цр, 0) | d0 ^ 0

s

при р ч те . По теореме 1 заключаем, что и(г) = 0 в К ^1 . Но тогда в силу аналитичности функции w(z ) = u(z) + iv(z ) заключаем, что v(z) вещественная постоянная. Пусть v(z) = а, тогда w(z) = ia. Лемма доказана.

3.    Основной результат

Пусть в односвязной области D С C задано дифференциальное уравнение Бель-трами fz (z) = ^(z)fz (z),                                       (13)

где p(z) — измеримая комплекснозначная функция, причем | p(z) | < 1 почти всюду в D.

Коэффициент p(z) = f _z (z)/f _z (z), напомним [1, c. 7], называется комплексной дилатацией отображения f (z), а условие (14) эквивалентно его локальной квазиконформности. В последние десятилетия уравнению Бельтрами было посвящено довольно много работ (см., например, [23; 24] и библиографию там). Это обусловлено тем, что уравнение Бельтрами (13) является одним из средств описания квазиконформных отображений и, кроме того, оно играет ключевую роль в задаче построения изотермических координат на двумерной поверхности (см. [2]).

Известно (см. [2, глава 2]), что при условии esssupp‘ |p(z)| < 1 во всякой подобласти D' ^ D,

уравнение (13) имеет гомеоморфное решение w = f (z), принадлежащее классу W l0 ’ _c2 вместе с обратным. Это решение единственно с точностью до суперпозиции с конформным отображением. Из данного факта и классической теоремы Римана вытекает, что для p(z) удовлетворяющего условию (14) либо существует решение f (z ) класса W lO ’ _c ² (вместе с обратным f ^-1 ) гомеоморфно отображающее D на круг В 1 , либо на всю комплексную плоскость C. В первом случае будем называть область D р-гиперболической, а во втором р-параболической. Всюду далее предполагается, что область D является µ-гиперболической.

Зафиксируем Z = ^(z) = a(z) + i e (z ) — произвольное решение (13) гомеоморфно отображающее D на единичный круг В 1 = { Z | Z G C, | Z | < 1 } .

Пусть Е ^ D — компактное подмножество и F = D \ Е кольцевидная область, внешняя часть границы которого совпадает с границей dD. Введем обозначения X _t = = ш ^-1 ( | ш | = t) = {z | z G F, | ^(z) | = 1 } , H^dz) — 1-мера Хаусдорфа в D.

Теорема 2. Пусть в F определено решение w уравнения (13). Если lim - t^i 1

-

- У | Rew(z) || ^ z (z) | H i (dz) s _t

= 0,

то w(z) = ia, где a G R .

Доказательство теоремы 2. Пусть Е ' = ш(Е) ^ В 1 . Зафиксируем произвольно 0 <  < R <  1, так чтобы Е ' лежало в круге B _r = { Z | Z G В 1 , | Z | <  R}. Для любых t 1 ,t ₂ , т.ч. R <  t 1 < t ₂ <  1 через K _{t 1} ,_t 2 будем обозначать кольцо K _{t 1} ,_t 2 = { Z | t 1 <  | Z | < t ₂ } , а через D _{t 1} ,_t 2 = w ^-1 (K _{t 1} ,_{t 2} ) его прообраз в D.

Положим W (Z) = w(^ ^-1 (z)); пусть w(z) = u(z) + iv(z), W (Z) = U (Z) + iV (Z). Функция W(Z) аналитическая в В 1 \Е ' , а значит и в Kr ^ . Обозначим I z , _z (z) якобиан отображения Z = w(z), то есть определитель

U,z ^{( z )} =

a^z) e^z)

a _y (z) ^e y ^(z)

^a x ^{(z) в} у ^{( z )     a} y ^{( z ) e} ^ ^{( z ) .}

Пусть t ₀ ,t 1 G (R, 1) (t ₀ <  t 1 ) — произвольны. Пользуясь формулой замены переменной в интеграле (см. [21]), имеем

У | U(ZWn = У | m(z) | I z ,z (z)dxdy.

^KW1               ^D *o Н

Далее, по формуле Кронрода—Федерера (см., например, [18; 20; 22]), имеем j \u(zWn >'■..

j \ u(z) \ I _c ,z (z)dxdy

D toti

ti j dtf \u (z)||dz|, to      St

I dt I ^|u C ^z ) ^|| _V ^Z^z⁾) || ^Hl(dz). t o     S t

Вычитая из равенства (18) равенство (17) и деля на t 1 — t ₀ , и учитывая (16), приходим к соотношению

[dt | /\u(V\\dz\ — [ |u(z)|   z,z(z) Hi(dz) | = 0.(19)

ti - to                                            \vl^(z)!\ to      SstSt

Устремляя t 1 ^ t ₀ + 0 и пользуясь известными свойствами интеграла Лебега, получаем при почти всех t ₀ Е (R, 1) равенство

I' иЩ\\Л\ = I' \u(z)\ ^(z) Hi(dz).(20)

V I W^(z)

St

Из (20) следует, что если

.'-—В u(z)^z® Hi(dz)=0,

St то для функции Ж(Z) выполнено условие (7) леммы 1 и значит Ж(Z) = ia, а — вещественная постоянная. Отсюда будет следовать утверждение теоремы. Покажем, что из условия (15) теоремы 2 вытекает (21).

Имеем \ w (z)\ = у/ (a(z)) ² + (e(z)) ² и почти всюду в Dr, 1

V \ ш(г) \ =

a(z) V a(z) + e(z) V e(z) \ M^z) \ ²

Отсюда

\ V \ ^(z )\ \ ² =

(ф^оЖ + М^^

^{( a ( z )) 2 + ( e ( z )) 2}

Для произвольной точки дифференцируемости z функции ^(z) рассмотрим следующую неотрицательно определенную квадратичную форму

B(X,Y ) = \ V a(z) \ ² X ² + 2 (V a(z), V e(z) ) XY + \ V e(z) \ 2 Y ² .

В силу известных свойств квадратичных форм имеет место неравенство

^•min У

B(X,Y ) X ² + Y ²

≤ λ

max ,

где hmm, Knax — наибольшее и наименьшее собственные значения матрицы квадратичной формы В(X, Y). Эти числа являются решениями следующего квадратного уравне- ния

¹ ? а ⁽}^{) 1}2( — K юй\ в^А ⁼⁰ ■■' ^А 2 - ^S (z) ^A + ( ⁵ (z)) ² = 0,       (24)

(a(z), p(z)) |Vp(z)|2 - K                       w \ \ где S(z) = |Va(z)|2 + |V₽(z)|2, (5(z))2 = |Va(z)|2|Vp(z)|2 — (a(z), p(z))2. С помощью простых выкладок нетрудно установить равенство

(5(z))2 = (ах(гЖ (г) — а, (г)вх« = (Iz,z (z ))2, то есть 5(z) = Iz,z (z). Решая квадратное уравнение (24), находим

S (г) — У (S (z )) ² — ..                      S (г) + ^(S (г)) ² — (6(г)) 2

.

^K min ^{( z )}                   2               , ^K max ^{( z )}                   2

Отсюда имеем

оценку

K (z) = S (z) — ^(S (z))2 — (5 (z))2 =              (5(z))2              > mm[                      2                 2(S(z) + ^(S(z))2 — (5(z))2) -

> (5(z)) ² .            (I z ,z (z)) ²

- 4S(z)     4( |V a(z) | ² + |V P(z) | ² )'

Используя соотношение

|Va(z)|2 + |VP(z)|2 = 2(H (z)|2 + И (z)|2), из (25), получаем оценку

А M >           (Iz ,z (z)) 2

^mM ) - 8(H(z) | ² + И(z) | ² )

(I z ,z (z)) ²          >  (I z z (z)) ²

8 | W z (z) | ² (1 + Hz) | ² ) - 16 | ^ z (z) | ² ■

Полагая в (23) X = a(z), Y = p(z) получим (22), следовательно из (26) вытекает, что

Mw(z) || - \      . ) - .^Л .. I z ,z (z) <  4 |V| w(z) ||K (z) | .          (27)

⁴K^{( z} ) |

Снова возьмем произвольно t ₀ ,t 1 E (R, 1), t ₀ 1 и воспользовавшись формулой Кронрода—

Федерера и оценкой (27), получим

0 <

t i

^t 0

/

Hz) | (4|V| w(z) ||| W z (z) | — I z ,z (z)) dxdy =

^0«1

t i — t o /^dt J | “^{( z )|} ^ '" ^{( z ) |}    M w(z) ||)^{K 1 ( dz )}.

t o      S t

Устремляя в этом неравенстве t 1 ^ t ₀ + 0, получаем неравенство верное при почти всех

^t o ^{E ( R} , 1)

4 / | «(z) | KWltf i (dz) - / | «(z) | 1^(4 ff i jdz). ^lv| ^^{( z ) l}|

^S t o                                    ^S t o

Из этого неравенства следует, что, если выполнено условие теоремы (15), то выполнено и условие (21), что и доказывает теорему. Теорема доказана.

Нетрудно показать (см. [13, стр. 235—236]), что вещественная и мнимая части решения w(z ) = u(z ) + iv(z) являются решениями дивергентного локально равномерно эллиптического уравнения

£ (a_n(^z)f _x ^(z ) + a i2 ^(z)f _y ( ^{z )}) + d^y (a 2i ^(z)f _x ^(z) + ^a 22 ^(z)^f y ( ^z )) = 0,

(1- µ 1 ) ² + µ ²₂                  (1+ µ 1 ) ² + µ ² ₂

^a 11 ^(z) =    1-| ц | 2    , ^a 22 ^(z) =     1-| ц | ²

a i2 (z) = a 2i (z) =

2 µ 2

1-| ц | ² ,

класса W lO ’ c ² , понимаемые в обобщенном смысле. Поэтому, по сути результат теоремы 2 касается обобщенных решений уравнений такого вида. Теоремам единственности для уравнений второго порядка эллиптического типа посвящена обширная литература, подробнее с этим можно познакомиться в [14; 19]. К этому же кругу вопросов примыкают теоремы о допустимой скорости стремления к нулю на бесконечности решений эллиптических уравнений второго порядка [15; 16].

4.    Благодарность

Автор выражает глубокую благодарность всем участникам семинара ”Геометриче-ский анализ и вычислительная геометрия” за обсуждение работы за полезные замечания и ценные рекомендации.