О фракционной модели накопления загрязняющих веществ в тумане

Накопление газообразных загрязняющих веществ в жидких аэрозольных частицах может оказывать сильное влияние на характер распространения примеси в атмосфере и осаждения на подстилающую поверхность Построение модели, учитывающей процессы взаимодействия аэрозолей и газообразных примесей, представляет собой актуальную задачу при исследовании переноса и рассеивания атмосферной примеси.

Моделирование процессов, происходящих в полидисперсной среде, строится на основе решения кинетического уравнения для функции распределения частиц по размерам [2, 3]. Для изучения накопления примеси в каплях аэрозоля в [3] получено аналитическое решение кинетического уравнения в предположении, что скорость изменения массы воды в каплях находится из формулы Максвелла для квазистатического испарения сферических капель, справедливой только для крупных капель, а скорость накопления примеси — по равновесному закону Генри. При этом в [3] пренебрегается нуклеацией, коагуляцией и дроблением капель. Обобщение полученного аналитического решения на случай произвольных скоростей конденсации и растворения примеси, а также учет взаимодействия капель вызывает затруднения. Использование метода моментов идя решения кинетического уравнения даже в случае отсутствия примеси, но с учетом зависимости скорости конденсации от размера капель, приводит к появлению заметной погрешности [2]. Поэтому представляется актуальным построение модели, способной описать накопление газообразной примеси в каплях аэрозоля в случае сильной зависимости скорости массообмена капель от их размеров, которая может быть легко обобщена на случай нескольких примесей.

Хорошо зарекомендовали себя при изучении процессов в полидисперсных средах фракционные модели (ФМ), когда весь спектр капель разбивается на конечное число фракций. При этом выделяют два подхода к построению ФМ — эйлеров и лагранжев [2]. С одноименными подходами в механике сплошных сред эти названия связаны только по принципу описания эволюции размеров капель. Эйлеров подход к построению ФМ предполагает постоянные размеры капель одной фракции (функция распределения капель по размерам аппроксимируется кусочно-постоянной функцией с неизменными интервалами однородности), при изменении размеров частица переходит в другую фракцию независимо от причины, вызвавшей это изменение. При лагранжевом описании размеры капель внутри одной фракции могут меняться за счет фазовых переходов на поверхности частиц, коагуляции или дробления (функция распределения капель аппроксимируется суммой конечного числа дельта-функций, которые могут смещаться по шкале размеров). Лагранжев подход позволяет более естественно описывать непрерывное изменение размеров капель, однако затрудняет учет нуклеации, в то время как эйлеров подход дает возможность простого учета зародышеобразования, но размер капель при этом меняется дискретно. В ФМ используется гипотеза о взаимопроникающих континуумах. что позволяет ввести для дисперсной фазы распределенную плотность и считать, что в каждой точке полидисперсная среда имеет несколько скоростей, температур и т.д. ФМ используются для изучения движения газа, с частицами конденсата в соплах [2], динамики облаков и туманов.

В представляемой работе предлагается эйлерова ФМ накопления газообразных примесей в каплях водного аэрозоля. Модель построена для произвольного разбиения капель на фракции, что позволяет учитывать коагуляцию капель без потери массы крупных капель даже при сравнительно небольшом количестве фракций. Одновременный учет накопления нескольких примесей позволяет исследовать химические превращения загрязняющих веществ в каплях туманов. В предложенной ФМ отсутствует ограничение малости массы примеси в капле, что расширяет рамки применения модели на высококонцентрированные примеси.

Построение фракционной модели

Введем функцию распределении капель /^,х. ц'¹^ но массе содержащихся в них воды д'⁰¹ и загрязняющих веществ |Д^и\ 7 = 1,5 в каждый момент времени t в произвольной точке рассматриваемой области £ кинетическое уравнение баланса в фазовом пространстве, аналогичное уравнению Лиувилля, можно записать в виде

Д +2            10;     ' )П ф1':                             со

Здесь второе слагаемое в левой части описывает перенос капель всех размеров со скоростью l/^x,^¹^, которая предполагается одинаковой для капель одной массы, третье слагаемое вписывает увеличение или уменьшение капель за счет фазовых переходов на поверхности гзлы сорбцию или десорбцию примеси жидкостью, при этом /"''^.г, р'^л1) — скорость изменения массы воды в калле; /^"(х, p^u^j — изменения массы /-той примеси в капле; первое слагаемое в правой части описывает гомогенную конденсацию, J(x) — (о;

скорость нуклеации капель, p.t ' — масса критического зародыша, произведение дельтафункций выражает предположение, что концентрации примесей в газовой смеси много меньше насыщающей, т.е. вновь образовавшиеся капли полностью состоят из воды, функционал С описывает взаимодействие капель - исчезновение мелких капель и увеличение количества крупных капель при коагуляции, обратные процессы при дроблении и т.п, функция Х^М*'') определяет химические превращения веществ внутри капель. Аргумент х указывает на зависимость скоростей процессов от полей температур (несущей среды и капель), концентраций (пара и примеси) и т. п. Принимается гипотеза об однородном распределении температуры и концентрации примеси по всему объему капель, при этом считается, что капли одной массы имеют равную температуру.

Величина «v = J---|^р<0)...р^' соответствует количественной концентрации о о капель (количество капель в единице объема) всех размеров, а величина pv - ] •■■ [//?'ti,p(l)\..plS' — распределенную плотность всей дисперсной фазы, при этом с о т = Ё р(:’ — полная масса капли

Аппроксимируем функцию /(?, х.ц^) кусочно-постоянной функцией по о) аргументам р следующим ооразом:

/■(/,X,pU)) = £ E                                                  (2)

/о,-о /5)=о       ’         «=о L где p0 =0 (Bq вводится для упрощения записи, pj сохраняет смысл массы критического зародыша, J w ^s, @0), й(-) — ступенчатая функция Хевисайда. Будем считать, что капли, удовлетворяющие неравенствам р^ s р < р'.ф+1, принадлежат к одной фракции. Температура и скорость всех капель, принадлежащих к одной фракции, предполагаются одинаковыми, равными соответственно (/.,„, /5) и Г,,. ^..Функционал взаимодействия капель и функция химического взаимодействия веществ предполагаются также независимыми от массы в пределах каждой фракции, а скорости изменения массы воды и примесеи Л(0; (s)^P у в пределах одной фракции зависят от р линейно.

Далее для краткости аргументы функций опускаются. Количественная концентрация капель каждой фракции определяется выражением

А                      i S .

а распределенная плотност ь соотношением

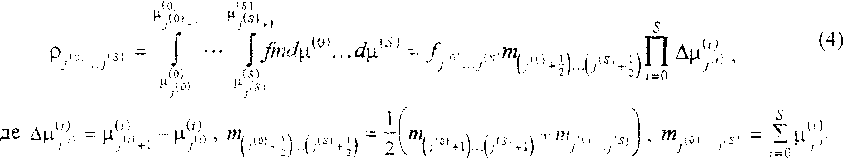
Используя символ Кронекера fl, если i = j, ^ij "j 0, если / # j

и интегрируя по массе воды и примесей в капле в пределах одной фракции уравнение (1), умноженное на массу капли, после использования аппроксимации (2) можно получить уравнение для распределенной плотности каждой фракции о          д

”'Р.Ж                                С|П5                    ,!У> +

ОГ -               (;Х -I                                 1/    , _{= 1} Т /

У У ;        1 - 2i/sgn| 1У

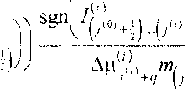
*qyV'v +

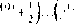
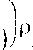
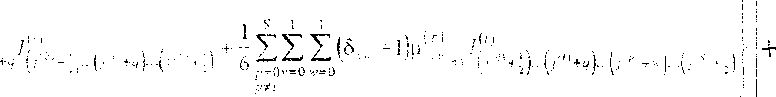
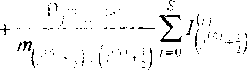
Здесь при q - -1 сумма в правой части описывает увеличение числа капель в рассматриваемой фракции за счет конденсации водяного пара и поглощения примеси каплями более малого размера, «у = 1 - испарения жидкости и выделения примеси каплями большего размера, при q -0 сумма описывает уменьшение количества капель за счет перехода в другие фракции. последнее слагаемое обусловлено изменением распределенной плотности за счет массообмена капель без перехода из одной фракции в Другую

Определению вида функций J, Г", ч и функционала о посвящено множество работ, среди- которых можно упомянуть классические теории: гомогенной нуклеации Френкеля-Зельдовича [1]; квазистатического испарения Максвелла [5]: коагуляции Смолуховского [4] и т. д. Не следует забывать, что величины J, о _(о; и / .. ,. являются функциями температуры капель и газовой смеси, концентрации пара и загрязняющего вещества, поэтому для полноты модель должна включать уравнения движения и энергии всей полидисперсной среды и каждой отдельной фракции, аналогичные приведенным в [2]. а также уравнения диффузии пара и примеси с соответствующими Источниковыми членами, которые должны описывать массообмен с каплями.

Решение полученной системы дифференциальных уравнений в частных производных вида (6), дополненной упомянутыми уравнениями, в общем виде представляет трудности с вычисли тельной точки зрения даже при небольших значениях N ' . Поэтому необходимы дополнительные упроглающие предположения. В качестве последних может выступать гипотеза об односкоростной среде [2] или более сильная гипотеза о неподвижной и однородной среде [3]. Считая концентрацию капель невысокой, можно пренебречь функционалом взаимодействия [2].

Коагуляцию, происходящую под действием броуновских сил, можно описать с помощью модели Смолуховского [4], в которой интенсивность взаимодействия капель зависит только от их размеров и диффузии, состав капель при этом может быть произвольным. Для капель, состоящих из нескольких веществ, можно записать

² i о ^=о v / ₍₇₎

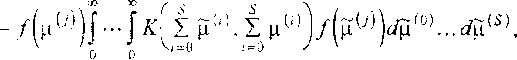
где К — коэффициент коагуляции, который определяется как вероятность столкновения капель различных размеров с последующим слипанием. Первый интеграл в правой части описывает увеличение числа крупных капель за счет слияния более мелких, а второй — исчезновение капель за счет коагуляции с каплями всех размеров.

Для простоты предположим, что

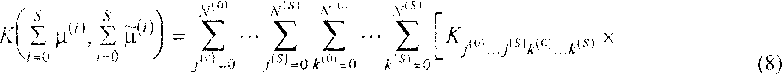
s / z                    W           М

>' П А             И - u(p) I Ai                           В

' 1Г'Цг                " /J'MH            + i U ’ го есть для любых двух фракций коэффициент коагуляции остается постоянным в пределах каждой из фракций.

Теперь, умножая (7) на массу капли, используя аппроксимации (2) и (8), интегрируя по массе в пределах каждой фракции, можно получить

— 2-2 2 - I W У ( Р«е ,=о ' vip 1 ,      f . (и . й) У (2)1+8-     (01+8 + пшуАи .,„, Ар*/,. Д ц^ * - цлр ~P/ni 2 " где иУ’ = тт^тах^Уц^ + ц^;),

- "-Ни Муй +Htl,iJ^y ^-Н; Д|+ (9) В       1    ( (')2-8,-     1>)2+8„     (1)2+8,,     0)2+5, 1 "Ид '-Цд? у+Нл- В - 4n+iJ ’ йУ - тах^^'Ут^р^,! + Ц^У,.цУ у :

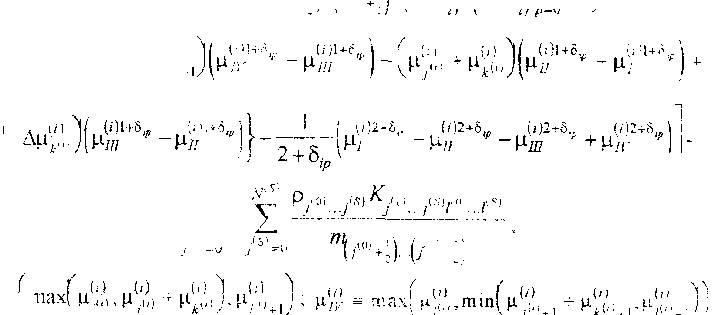
М • (       7 (?)     • К О)         О)     (i) (О 1)(г)

Цу = min max цуфтт! ц?н + uillb + u;

■ I          Г (У f (1)             и)      it)       ,     (Г)'

цу $ mini maxi,                ]■

Громоздкий вид первой суммы в правой части обусловлен произвольностью выбора Лц1 J , что позволяет сократить количество фракций, что, в свою очередь, приводит к повышению эффективности расчетов.

Расчет простейшего случая

Для иллюстрации применения разработанной модели рассмотрим простейший модельный случай накопления одного загрязняющего вещества в водном тумане без химических реакций Среда предполагается неподвижной и однородной, температурными эффектами пренебрегаем. Скорость конденсации пара определяется формулой Максвелла

710’ - 4лП!0У(с^‘                                    О °)

где D" коэффициент диффузии пара, г - ^Згп / 4лр^ — радиус капли, форма которой предполагается сферической, р.к плотность жидкости капли, сС1 — концентрация пара. с\ ’ — равновесная концентрация пара при данной температуре. Тогда для J'/ ;11

можно записать выражение rW

1 ,(0) Д'

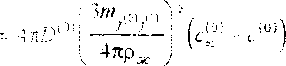
Скорость накопления примеси как и в [1], определяется равновесным законом Генри

С! - 4лА)иФ| с(1) - -----—                                 (■ 12)

V 4тп" Н ;

где £)'" — коэффициент диффузии примеси, с" — концентрация примеси, Н безразмерная константа Генри. Отсюда можно получить выражения для 1 Д,:

5т

Г'.пР,

Коэффициент коагуляции определяется соотношением [41

в

неподзил

среде для сферических частиц радиусы капель с вязкость среды.

сами т.т

к

постоянная Больцмана, 7, v

Далее будем считать, что происходит только конденсация и поглощение примеси /:'с. ,s, > 0, процессом нуклеации пренебрегаем (./ = 0).

Как указывалось выше, полученную систему дифференциальных уравнений необходимо дополнить уравнениями диффузии пара и примесей, которые с учетом высказанных предположений об однородности и неподвижности среды могут быть записаны в виде

д(^|ф0)_.                                j                                 ■ (15)

При расчетах принималось, что вязкость среды и коэффициенты диффузии не зависят от состава и температуры В начальный момент все капли имеют размер критического зародыша, при этом я₁₀ = 2 ■ 10⁵ см ', с ¹¹ = 5 -10^ г(см^г , с'" = КГ⁹ г! см³, Т - 237.15 К. Подобные условия могут реализовываться при образовании радиационного тумана, который возникает при более быстром ночном охлаждении поверхности земли за счет лучеиспускания по сравнению с малоподвижным воздухом над ней [1]. Рассматривалось 400 фракций ( N^[0> = 40, N^v- =10). Полученная система обыкновенных дифференциальных уравнений решалась методом Рунге-Кутта четвертого порядка аппроксимации.

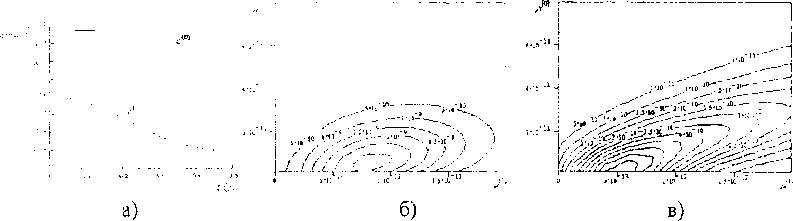
Рис. 1 Зависимость концентрации пара и примеси от времени (а) и распределенная плотность дисперсной фазы, полученная без учета коагуляции (б) и с учетом коагуляции (в)

На рис. 1(6,в) представлена распределенная плотность фракций капель в зависимости от содержания в каплях воды и примеси в момент установления равновесной концентрации примеси и пара На графике видно, что первоначально практически монодисперсная примесь с течением времени стала полидисперсной, и при этом содержание примеси в каплях одинаковой массы может быть различно. На рис 1(a) приведена зависимость концентрации пара с'"" и примеси с'0 от времени Для установления равновесной концентрации при постоянной температуре требуется время порядка половины секунды.

Выводы

Построена эйлерова фракционная модель, описывающая процессы накопления примеси в каплях туманов для произвольных скоростей конденсации, поглощения примеси, нуклеации и т.н Модель допускает возможность неравномерного разбиения на фракции, что позволяет существенно сокращать их количество.

В отличие от решения, полученного в [3], в представленной модели не требуется априорного знания функции распределения капель по полной массе: напротив, это распределение получается в результате решения В отличие от [3] отсутствует также ограничение на массу примеси в капле.