О гравитационно-конвективной неустойчивости в коллоидах

На основании того, что в полостях высотой порядка сантиметра однородность магнитного коллоида сохраняется несколько недель, влияние неоднородностей концентрации, вызванных гравитационной седиментацией частиц, на конвекцию считается пренебрежимо малым, и в большинстве публикаций [1–6] магнитная наножидкость рассматривается как гипотетическая однокомпонентная среда.

Однако обнаруженные в экспериментах по исследованию тепловой гравитационной конвекции в магнитной наножидкости "жесткое" ветвление и колебательный характер течения свидетельствовали о наличии неоднородностей концентрации [7–14]. Согласно утверждению авторов первых экспериментов по изучению гравитационной седиментации частиц и их агрегатов, в отсутствие магнитного поля профиль концентрации не менялся в течение часов и даже дней [15]. В дальнейшем возникновение перепадов концентрации вследствие седиментации частиц и агрегатов в поле тяжести было подробно исследовано в экспериментах и расчетах [16–18].

Следует отметить, что при изучении конвективных течений коллоидов обычно исходят из оценки, рассматривающей время

разрушения первоначально однородного состояния t = h²/D как время, по истечении которого концентрация частиц в верхней и нижней частях полости будет отличаться в е раз [2], где е – основание натурального логарифма. Вследствие того что тепловая конвекция возбуждается малыми перепадами давления, перепады плотности, вызванные седиментацией частиц и агрегатов и влияющие на течение, формируются за значительно меньшие времена [16].

В теории влияние градиентов концентрации, заложенных в начальное состояние системы, на конвективную неустойчивость в коллоидах рассмотрено в работах [11, 12]. Однако согласно работе [19] колебательная конвекция размывает первоначальный концентрационный профиль и в коллоиде устанавливается стационарное течение, в то время как в экспериментах колебательная конвекция сохранялась в течение всего времени наблюдения – от суток до месяца [7–14]. Это расхождение представляется важным как при построении адекватных теоретических моделей конвекции в коллоидах, так и для практического использования наножидкостей в различных датчиках и теплообменных устройствах, где колебания будут являться источником погрешностей и нестабильности.

Помимо градиентов концентрации, индуцируемых гравитационной седиментацией частиц, на конвективную неустойчивость в магнитных коллоидах могут оказывать влияние градиенты концентрации термодиффузионной природы [20–22]. Действие термодиффузии на конвекцию в магнитных наножидкостях рассмотрено в расчетах [23, 24], в которых обнаружена возможность существования как стационарных [23], так и колебательных режимов конвекции [24].

Однако в реальных условиях градиенты плотности теплового, барометрического и термодиффузионного происхождения действуют одновременно, и необходимо рассматривать их совместное влияние на конвективную устойчивость и течение магнитной жидкости.

1.    Методика эксперимента

Измерение тепловых потоков при помощи интегрального датчика производилось в конвективных камерах цилиндрической формы, подробно описанных в работе [10]. Полости с магнитной жидкостью высотой h = 2.00 ± 0.05 мм или 5.00 ± 0.05 мм и диаметром 75 мм располагались между медными теплообменниками толщиной 10 мм и диаметром 98 мм. Между медными пластинами нижнего теплообменника располагался интегральный датчик теплового потока в виде фторопластовой прокладки толщиной 0.2 мм в первой полости и 2.0 мм – во второй. Коэффициенты теплопроводности меди и фторопласта равны 4.0·10² и 0.25 Вт/(м·К)). Магнитные жидкости, применявшиеся в опытах, имели коэффициент теплопроводности 0.15– 0.21 Вт/(м·К). Отношение коэффициентов теплопроводностей магнитной жидкости и меди порядка 10^-4. Таким образом, медный массив с высокой точностью удовлетворял приближению бесконечной теплопроводности, часто используемому в теории.

Высота фторопластовой прослойки была выбрана значительно меньшей толщины слоя h с той целью, чтобы возможно большая доля температурного перепада, который мог быть приложен к теплообменникам в кювете данной конструкции (до 85 К), приходилась на рабочий слой с жидкостью. Все детали кюветы стягивались тремя латунными болтами диаметром 5 мм, изолированными от металлических пластин фторопластовыми втулками и текстолитовыми шайбами. Этим исключался паразитный тепловой поток по соедини- тельным винтам от одного теплообменника к другому.

Интенсивность течений определяли методом Шмидта–Милвертона [25] по поперечному теплопереносу через слой жидкости, сравнивая разность температур между его границами Δ Т с падением температуры на твёрдой прослойке Δ Т ^′ .

В стационарных и медленно меняющихся условиях, когда распределение температуры в прослойке линейно по вертикали, число Нуссельта Nu , равное отношению полного теплопотока, включающего конвективную и молекулярную составляющие, к чисто молекулярному теплопереносу, вычислялось из выражения: Nu = k Δ T '/ Δ T . Здесь k – эмпирическая постоянная, имеющая смысл отношения эффективных теплопроводностей жидкости и фторопласта и вычисляемая в отсутствие конвекции из равенства k Δ T ′ = Δ T .

2.    Результаты эксперимента

В изотермическом коллоиде даже в отсутствие макроскопических движений происходит гравитационное осаждение и диффузионное перераспределение частиц. В неизотермических условиях к вышеназванным явлениям добавляется термодиффузия. Поэтому полное механическое равновесие в коллоиде не имеет места и лучше говорить о квазиравновесии.

Рассмотрим термоконвективную устойчивость квазиравновесия для коллоидов с различными концентрациями магнитной фазы. В опытах использовались магнитные жидкости на основе керосина с намагниченностями насыщения  MS = 20; 37 и 55 кА/м и плотностями    ρ = 0.98·103, 1.26·103     и

• 1.55·10³ кг/м³.

Обозначим через ΔΤ _C критическую разность температуры между горизонтальными границами полости, при которой механическое квазиравновесие коллоида теряет устойчивость.

При h = 2.0 мм для жидкостей с ρ = 0.98·10³, 1.26·10³ и 1.55·10³ кг/м³ разности температур ΔΤ C составляли 4.5; 7.5 и 25.0 К. Конвекция возбуждалась мягко и носила стационарный характер.

На рис. 1 представлена зависимость числа Нуссельта Nu от относительного перепада температуры ΔΤ / ΔΤ C для коллоидов с различной концентрацией магнитной фазы (обозначения 1- 3) для слоя с h = 2.0 мм. В опытах с концентрированным коллоидом ( ρ = 1.55·10³ кг/м³) вследствие большой вязкости и, соответственно, высоких значений ΔΤ _C данные по конвективному теплопереносу удалось получить в промежутке до ΔΤ / ΔΤ C = 2.0. В слабоконцентрированном коллоиде ( ρ = 0.98·10³ кг/м³) при малых ΔΤ _C теплоперенос представлен до ΔΤ / ΔΤ C = 6.0.

Из графика видно, что при ΔΤ / ΔΤ C <  3.0 значения теплового потока для всех магнитных жидкостей в пределах погрешности укладываются на одну линию.

Отметим, что значения числа Nu для магнитной жидкости совпадают с результатами, взятыми из опытов с однокомпонентными средами: водой (обозначения 4) и гелием (обозначения 5) [26].

В отличие от тонкого слоя ( h = 2.0 мм) в опытах с полостью толщиной h = 5.0 мм конвекция в коллоидах возникает жестко и с гистерезисом (рис. 2). При постепенном увеличении перепада температур между теплообменниками разность температур, при которой возбуждалось конвективное течение, менялась в зависимости от предыстории опыта. При понижении разности температур возвращение от конвекции к неподвижному состоянию совершалось при воспроизводившемся в разных опытах значении ΔΤ _С , которое будет использоваться при дальнейшем представлении результатов.

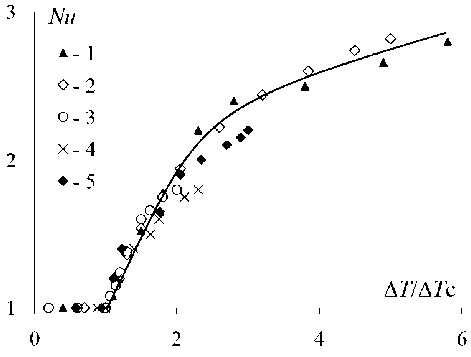
Рис. 1. Зависимость теплопереноса от относительного перепада температуры в горизонтальном слое (h = 2 мм): 1; 2 и 3 – для магнитных коллоидов с ρ = 0.98·10³, 1.26·10³ и 1.55·10³ кг/м³; 4 и 5 – для воды и гелия [26]

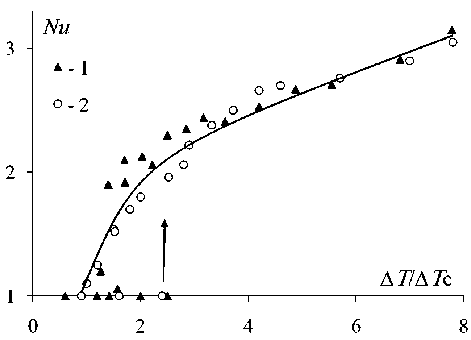
Рис. 2. Зависимость теплопереноса от относительного перепада температуры в горизонтальном слое (h = 5 мм): 1 – ρ = 0.98·10³ кг/м³, ΔΤ C = 0.63 К; 2 – ρ = 1.55·10³ кг/м³, ΔΤ C = 2.5 К

Вертикальной стрелкой на рис. 2 показано жесткое возбуждение конвекции при пошаговом повышении температуры на слое жидкости. Глубина гистерезиса могла меняться от десяти (для жидкости, предварительно перемешанной конвективным течением) до двухсот и более процентов (для коллоида, находившегося в покое) от ΔΤ С . Возвращение к механическому квазиравновесию из области интенсивной конвекции происходит при воспроизводимых значениях разности температур, составлявших для коллоидов     с     плотностями     0.98·10³

и 1.55·10³ кг/м³ ΔΤ С = 0.63 К и 2.5 К соответственно.

Заключение

Следует отметить, что сложное поведение наножидкостей различного состава и предназначения является актуальной проблемой в теории тепло- и массопереноса [26–28].

Как показывают эксперименты, гравитационно-конвективная неустойчивость наносуспензий обусловлена конкуренцией между градиентами плотности тепловой, термодиффузионной и барометрической природы.

В тонких слоях при относительно высоких критических перепадах температуры наблюдается мягкое ветвление конвекции для коллоидов с разным содержанием магнитной фазы. В таких ситуациях наряду с архимедовским механизмом конвекции существенное влияние оказывает термофорез частиц, приводящий при положительном знаке коэффициента термодиффузии [20–22] к дополнительной дестабилизации.

В слоях большей толщины ( h > 2.0 мм) конвекция в коллоиде возникает при меньших ΔΤ C и термодиффузионные эффекты будут играть меньшую роль. В этих случаях решающее влияние на устойчивость механического квазиравновесия оказывает седиментация частиц и агрегатов, задерживающая возникновение конвективного движения.