О классах гиперфункций ранга 2, порожденных максимальными частичными ультраклонами

В последние десятилетия активно исследуются мультифункции. Под мультифункцией на k-элементном множестве A понимается функция, определенная на множестве A и принимающая в качестве значений его подмножества. Очевидно, что суперпозиция в обычном смысле при работе с мультифункциями не подходит. Поэтому для них необходимо дать новое определение суперпозиции. Обычно рассматривается два способа определения суперпозиции: в основе первого лежит объединение подмножеств множества A, и в этом случае замкнутые множества, содержащие все проекции, называются мультиклонами, а в основе второго — пересечение подмножеств множества A, и замкнутые множества, содержащие все проекции, называются частичными ультраклонами. Множество мультифункций на A, с одной стороны, содержит в себе все функции к-значной логики, а с другой — является подмножеством функций 2k -значной логики с суперпозицией, сохраняющей это подмножество.

В теории функций интересной является задача классификации. Одним из известных вариантов классификации функций к -значной логики является тот, при котором функции в замкнутом подмножестве B замкнутого множества M могут быть разбиты согласно их принадлежности предпол-ным в M классам. В данной работе в роли подмножества B выступает множество всех гиперфункций на двухэлементном множестве, а в качестве множества M — множество всех мультифункций на двухэлементном множестве, и при этом предполными классами являются максимальные частичные ультраклоны. Используя разбиение на классы эквивалентности по отношению принадлежности максимальным классам, можно оценить мощности всевозможных базисов и описать все типы базисов.

Отметим, что классы эквивалентности и типы базисов для различных множеств функций к -значной логики изучались, например, в [4; 5; 6; 7].

1 Основные понятия и определения

Пусть E = { 0,1 } и F = { 0 , { 0 } , { 1 } , { 0,1 }} . Определим следующие множества функций:

P{, . = { f\f : E" ^ F } . P 2 = U P - . ,

n

P^ = { f l f : E " ^ F \ { 0 } } , P   U P; n ,

n

p * , = { f\f : Eⁿ ^ f \ {{ o,i }} } , P = u p:, , n

P ,_ n = { f \ f : E " ^ E } , P 2 = U P 2, " . n

Функции из P ₂ * называются мультифункциями на E , из P₂ — гиперфункциями на E , из P ₂ ^* — частичными функциями на E , из P ₂ — булевыми функциями.

Для того чтобы суперпозиция f ( f 1 ( x 1 ,...,x_n ),..., f m ( x 1 ,..., x_n )) определяла некоторую мультифункции g ( x 1 ,..., x_n ) определим значения мультифункции g на наборах из подмножеств множества E .

Если ( a 1 ,...,a n ) е E n , то по определению

I f ( ь , .-. b m );

g ⁽ й ^..., a n ) = ^ '

^е fi ^{( a} 1 ,.••, a , )

U f ( b l ,..., b m ),

_ b e fj ( a i,..., a n )

пересечение берется, если оно не пусто, в противном случае берется объединение. На наборах, содержащих пустое множество, значение мультифункции равно пустому множеству.

Это определение позволяет вычислить значение мультифункции на любом наборе ( a₁,...,a n ) е Fⁿ .

Для упрощения записи договоримся использовать кодировку: 0 ^ *, {0} о 0, {1} о 1, {0,1} о - .

Константную гиперфункцию, принимающую на всех наборах значение -, обозначим через f - .

Отметим, что в настоящей работе мы будем придерживаться терминологии, принятой в [1; 2], что позволит нам здесь не вводить дополнительных определений.

В [1] доказано, что максимальными частичными ультраклонами ранга 2 являются только следующие 12 множеств:

• 1)    K 1 — множество, состоящее из всех мультифункций f принимающих на нулевом наборе либо значение 0, либо значение *;

• 2)    K 2 — множество, состоящее из всех мультифункций f принимающих на единичном наборе либо значение 1, либо значение *;

• 3)    K 3 — множество, состоящее из всех мультифункций f, для которых выполняется одно из двух условий:

~         ~

• •    f (0) = * или f (1) = * ;

• •    f (0) = 0 и f (1) = 1 .

• 4)    K 4 — множество, состоящее из всех мультифункций f, таких, что на любом двоичном наборе а выполняется одно из трех условий:

• •    f ( о с) = f о = - ;

• •    f ( о с) = f ( S ) = * ;

• •    f ^о ) = f ⁽ a ) , где f (<~) ^{е { 0,1 }} .

• 5)    K 5 — множество, состоящее из всех мультифункций f, таких, что на любом двоичном наборе о с выполняется одно из двух условий:

• •    f ( о с) = * или f ( о с) = * ;

• •    f(о) = f ⁽ « ) , где f («) ^{е { 0,1 }} .

• 6)    K ₆ = P , ^- u { * } ;

• 7)    K 7 = P 2 ;

• 8)    K 8 — множество всех мультифункций f, одновременно удовлетворяющих трем условиям:

• если f ( a ), f (Д), f (~) е { 0,1 } , то

/ ~\ a fr0) r01 r01 Г1!! f P е ^ 0 0 1 1 >, где a,P,у — двоичные наборы, такие V Y / V 0 v V/ V 0 / i V/ что (aiPiy i) е {(000), (001), (010),(111)} для любого i е {1,...,n};

• •    если существует двоичный набор a , такой, что f ( a ) = - , то для любого двоичного набора P верно f ( P ) * 1 ;

• •    пусть двоичные наборы a , в такие, что a i <  P i для всех

  ,...

  
  

~

, n } , тогда, если f (a) = * , то f ( P ) = * .

• 9)    K 9 — множество всех мультифункций f одновременно удовлетворяющих трем условиям:

• • если f ( a ) f ( P ), f (~) е { 0,1 } , то

  ~\ ^a

  ^{f P}

  V ~ /

  
  

  е

  
  

  <

  
  

  Г ⁰ 1

  0 о V^й/

  
  

  ,

  
  

  Г ⁰ 1 1

  V¹/

  
  

  ,

  
  

  ^{Г 1 1}

  
  

  ,

  
  

  V¹/

  
  

  1 V/

  
  

  ~

  > , где a , P , у — двоичные наборы, такие,

  
  

  что ( a i P i y i ) е { (000), (011),(101),(111) } для любого i е { 1,..., n } ;

  • •    если существует двоичный набор a , такой, что f ( a ) = - , то для

  
  

  ~

  
  

  ~

  
  

  любого двоичного набора P верно f ( P ) * 0 ;

  • •    пусть двоичные наборы a , P такие, что a i <  P i для всех

  
  

  ,...,

  
  

  ~

  n } , тогда, если f ( P ) = * , то f ( a ) = * .

  
  

  • 10)    Кю — множество всех мультифункций f, сохраняющих предикат:

  
  

  R 10

  
  

  Г 0 • 1 0

  
  
  
  

  можные столбцы, в творяют двум условиям:

  
  

  0	1	1	1 1 -	a
  1	1	1	0 0 -	P
  1	1	0	10 -	Г
  0	1	0	01 -	5
  которых			a , P, у , 5 е	{0,

  , где ( aPy5 ) t

  
  

  Л

  
  

  _—

  
  

  всевоз-

  
  

  /

  • ¹, 1, - ,* } одновременно удовле-

  
  

11) K 11 — множество всех мультифункций f, сохраняющих предикат:

	' 0	0	0	1	1	0	0	—	—	0	1	—	*	*	*	*	*	*	* '
R 11 =	0	0	1	0	1	0	—	0	—	*	*	*	0	1	—	*	*	*	*
	. 0	1	0	0	1	—	0	0	—	*	*	*	*	*	*	0	1	—	* 7

12) K 12 — множество всех мультифункций f, сохраняющих предикат:

'0 0 1 1 11 1--0 1 — * * * * * * *5 R12 = 0 1 0 1 11 — 1 — ***01 — * *** . .0 1 1 0 1 — 1 1 — ****** 0 1 — *7 Далее для каждой мультифункции f однозначно определим вектор принадлежности т(f) = (т1,...,т12) множествам K1 - K12, в котором для всех i g {1,...,12} компонента т. равна 0, если f g Ki, и равна 1, если f ^ к,.

Отношение принадлежности множествам K 1 - K 12 является отношением эквивалентности и порождает разбиение P ₂ * на классы эквивалентности. У мультифункций из одного класса векторы принадлежности множествам K - K 12 совпадают. Так как число максимальных частичных ультраклонов равно 12, то наибольшее возможное число классов эквивалентности равно 2 ¹² = 4096.

В данной работе найдем число классов эквивалентности, которые состоят только из гиперфункций.

f (,6) = Л е { 0,1 } . Тогда f

/ ~\

a

e

V ^e /

—

—

Л

V Л )

t R ₁₀ , при этом для всех

,...,

n } набор ( a i a i P i PP t принадлежит предикату R ₁₀ .

• 3.    Справедливость утверждения следует непосредственно из определений классов K 1 , K 2 , K 3 .

Лемма доказана.

Лемма 2. Для любой f е P₂ \ Р ₂ справедливы утверждения:

• 1)    если f t K ₈ , то f t K 11 ;

• 2)    если f t K ₉ , то f t K ₁₂ .

Доказательство. 1. Пусть f t K ₈ . Предположим, что f не удовлетворяет первому условию в определении класса K 8 . Найдутся наборы a ¹ , где i е { 1,2,3 } ,такие, что столбец ( a j a 2 a j ) t совпадает с одним из столбцов

(000) t ,(001) t ,(010) t ,(111) t

для любого j е { 1,

. . .

, n }

и

/ ~1 А a

f a

е

~3

V a /

' ¹ '

о V /

,

V1/

,

' ¹ '

V/

,

' ¹ '

о kv/

г ~i л a

f

a

~3

V a /

е <

V/

,

' ¹ '

V/

,

1 о V /

Г , то,

учи-

тывая, что (000) t ,(001) t ,(010) t ,(111) t е R _n,

получим f t K ₁₁ .

Если

a

f a

~3

_V a _/

' ¹ '

о V /

, то

/ ~1 Л

f в

~ 3

V ^a /

—

n \/

~ t R11, где набор в такой, что Pk =

—

для тех к , для которых ( a^a^a^ t = (010) t , и P k = a k для остальных k .

Следовательно, f t K ₁₁ .

Теперь предположим, что f не удовлетворяет второму условию в определении класса K8. Найдутся наборы a1 и a2, такие, что f (с11) = — и f ((~2) = 1. Рассмотрим значение f на единичном наборе. Если f (1) е{0,1},   то

/ ~1 Л

~ f 1

~ 1

_{V a} 1 1 _/

е

<

,

—

V/

—

—

V/

~.

>t R 11 . Если f (1) = — , то

/ —

a

2 Л

Г1)

f

—

к

a

к ¹

t R 11 . Следовательно, f t K 11

• 2.    Доказательство аналогично доказательству предыдущего пункта в силу двойственности.

Лемма доказана.

Лемма 3. Для любой f е P₂ \ Р ₂ справедливы утверждения:

• 1) если f е K 1 , то f t K 9 и f t K 12 ;

• 2) если f е K 2 , то f t K ₈ и f t K _n ;

• 3) если f е K . n K₂ , то f t K u K₉ и f t K, , u K. ₂ .

• 2.    Доказательство аналогично доказательству предыдущего пункта в силу двойственности.

• 3.    Справедливость утверждения следует из пунктов 1 и 2 настоящей леммы, а также пунктов 1 и 2 леммы 2.

z               J           1           2 ^J J            о          9 «z           11          12

Доказательство. 1. Пусть гиперфункция f е K 1 . Тогда f (0) = 0 , т. е. существует набор, на котором значение f равно 0. Поэтому, учитывая обязательное существование набора, на котором значение функции f равно -, получим, что гиперфункция f не удовлетворяет второму условию в определении класса K 9 . Следовательно, f t K ₉ и в силу пункта 2 леммы 2 получим, что f t K ₁₂ .

Лемма доказана.

Лемма 4. Пусть f е P₂ \ Р ₂ . Если f е K 1 \ K ₂ или f е K ₂ \ K 1 , то f t K ₄ .

Доказательство. Пусть, для определенности, f е K1 \ K2 . Тогда f(0) = 0 и f(1) е {0,-}. Покажем, что в каждом случае гиперфункция f не удовлетворяет условиям в определении класса K4. Если f(1) = 0, то f (,—) = f (—) = 0 ^ 1 = f (0) = f(1). Если же f(1) = -, то f (1 ) = f (0) = 0 ^ -. Для случая, когда гиперфункция f принадлежит множеству f е K2 \ K1 , доказательство аналогично.

Лемма доказана.

Лемма 5. Для любой f е P₂ \ Р ₂ справедливы утверждения:

• 1)    если f е K ₈ n K ₉ , то гиперфункция f является константной гиперфункцией f - ;

• 2)    если f е K _н n K ₁₂ , то гиперфункция f является константной гиперфункцией f - .

• 2.    Предположим, что гиперфункция f не является константной гиперфункцией f ^- . Из предыдущего пункта получим, что либо f t K ₉ , либо f t K ₈ . Далее, используя утверждения леммы 2, получим, что f t K ₁₂ либо f t K 11 , что противоречит принадлежности f множеству K ii n K 12 .

Доказательство. 1. Предположим, что гиперфункция f не является константной гиперфункцией f ^- . Тогда существует набор a , такой, что f ( a ) = Хе { 0,1 } . При этом обязательно найдется набор, на котором значение f равно -. Поэтому если Х = 0 , то f не удовлетворяет второму условию в определении класса K 9 , если же Х = 1 , то f не удовлетворяет второму условию в определении класса K 8 . Следовательно, либо f t K ₉ , либо f t K ₈ , что противоречит принадлежности f множеству K ₈ n K ₉ .

Лемма доказана.

Лемма 6. Пусть f е P ₂ \ P ₂ . Если f t K 1 u K ₂ и f е K ₄ , то либо гиперфункция f является константной гиперфункцией f - , либо f t K, u K_q u K_n u K. ₂ . J         8        9        11        12

Доказательство. Так как f t K 1 u K2, то f (0) е {1,-}  и f (1) е{0,-}. С учетом того, что f е K4 остаются варианты f (0) = 1, ~.                                 ,~.                                                              ,~.

f (1) = 0 и f (0) = f (1) = - . В случае когда f (0) = 1 , f (1) = 0 , также как и в доказательстве леммы 3, получим, что f t K ₈ u K ₉ u K 11 u K ₁₂ . Если же f (0) = f (1) = - , то либо f является константной гиперфункцией f ^- и утверждение леммы справедливо, либо существует набор a , такой, что f ( a ) = Хе { 0,1 } . Без ограничения общности можно считать, что f (~) = 0 . Так как f е K ₄ , то f ( < ~) = 1 . Таким образом существуют наборы, на которых f равна 0, 1 и -. Следовательно, f t K u K u K u K . 8         9         11         12

Лемма доказана.

Лемма 7. Пусть   f е P₂ \ Р ₂ . Если f t K 1 u K ₂   и f t K ₄ ,

• f t K 11 u K 12 .

Доказательство. Так как f t K 1 u K2, то f (0) е {1,-} и f (1) е {0,-}. Если f (0) и f (1) одновременно не равны -, то получим z~\ f0

~

f 1

V 7

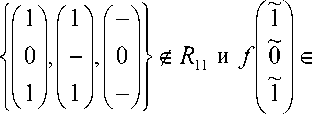
A ⁰ ) i .1 0 7

f ⁰ ) -

V ⁰ 7

-

i rt R 12 .

V 7

~~

Предположим, что f (0) = f (1) = - . Так как f t K4, то f не являет ся константной гиперфункцией f и, следовательно, найдется набор ~~,

~

( л -

такой, что     f ( a ) = 2 6 { 0,1 } .    Тогда

~

f a

2 t R_n

и

f

0 V7

V7

~

г—

а

~

V

( Л -

2 t R 12 .

V7

Лемма доказана.

Далее докажем две основные теоремы.

Теорема 1. Множество всех гиперфункций ранга 2, отличных от булевых функций, порождает не более 13 классов эквивалентности относи- тельно принадлежности максимальным частичным ультраклонам.

Доказательство. Из первых двух пунктов леммы 1 следует, что для каждой из рассматриваемых гиперфункций в векторе (т1т2т3т4т5 01т8т9т10т11т12) принадлежности максимальным частичным ультраклонам K1 - K12 компоненты т5 и т10 равны 1, а из третьего пункта этой же леммы получим, что набор (т1т2т3) совпадает с одним из наборов (000), (011), (101), (111). Рассмотрим все эти варианты.

Из третьего пункта леммы 3 следует, что гиперфункции, принадлежащие одновременно классам K 1 , K 2 , K 3 , разбиваются не более чем на 2 класса эквивалентности, которым соответствуют векторы (000010111111), (000110111111).

Теперь рассмотрим гиперфункции, которые либо принадлежат K 1 и не принадлежат K 2 , K 3 , либо принадлежат K 2 и не принадлежат K 1 , K 3 . Применяя лемму 2, первые два пункта леммы 3 и лемму 4, получим, что число классов эквивалентности для таких гиперфункций не более 6 и векторы, соответствующие этим классам, имеют вид (011110101101), (011110101111), (011110111111), (101110110110), (101110110111), (101110111111).

Осталось рассмотреть гиперфункции, не принадлежащие ни одному из классов K1, K2, K3. Очевидно, что среди таких гиперфункций выделяются те, которые на каждом наборе принимают значение –. Легко проверить, что вектор принадлежности классам K1 – K12 для этих гиперфункций име- ет вид (111010100000). Далее предполагаем, что гиперфункции неконстантные. По лемме 6 получим, что гиперфункции, принадлежащие классу K4, могут порождать не более одного класса эквивалентности, которому соответствует вектор принадлежности (111010111111). Далее, применяя леммы 5 и 7, получим, что гиперфункции, не принадлежащие классу K4, разбиваются не более чем на 3 класса эквивалентности, которым соответствуют векторы (111110101111), (111110110111), (111110111111).

Теорема доказана.

Теорема 2. Множество всех гиперфункций ранга 2 порождает 28 классов эквивалентности относительно принадлежности максимальным частичным ультраклонам.

Доказательство. Так как число классов булевых функций равно 15, с учетом предыдущей теоремы получим, что все гиперфункции разбиваются не более чем на 28 классов эквивалентности.

В результате компьютерных вычислений над гиперфункциями от трех переменных были найдены 28 различных векторов принадлежности классам K 1 – K 12 . В таблице 1 приведены векторы принадлежности и соответствующие им гиперфункции.

Теорема доказана.

Таблица 1

№	r ( f )	f ( X 1 , x 2 , x 3 )	№	r ( f )	f ( X 1 , x 2 , x 3 )
1	(000000000000)	(00001111)	15	(101110000000)	(11111111)
2	(000000011011)	(01101001)	16	(101110011011)	(10011001)
3	(000000011111)	(00010111)	17	(101110011111)	(10000001)
4	(000010111111)	(000--111)	18	(101110110110)	(-1111111)
5	(000110001101)	(00000001)	19	(101110110111)	111111-1)
6	(000110010110)	(00111111)	20	(101110111111)	(100000-1)
7	(000110011111)	(00000111)	21	(111000011011)	(10010110)
8	(000110111111)	(000000-1)	22	(111000011111)	(10001110)
9	(011110000000)	(00000000)	23	(111010100000)	f
10	(011110011011)	(00111100)	24	(111010111111)	(100--110)
11	(011110011111)	(00000010)	25	(111110011111)	(10000000)
12	(011110101101)	(0000000-)	26	(111110101111)	(-0000000)
13	(011110101111)	(000000-0)	27	(111110110111)	(1111111-)
14	(011110111111)	(0000001-)	28	(111110111111)	(1000000-)

Заключение

Результат, полученный в данной работе, является существенным для дальнейших исследований разбиения множества мультифункций на двухэлементном множестве на классы эквивалентности относительно принадлежности максимальным частичным ультраклонам. Получив полное разбиение, можно перейти к решению задачи оценивания мощности всех возможных базисов и подсчета количества различных типов базисов одинаковой мощности.