О клонах ультрафункций, сохраняющих нуль и единицу

Пусть E = { 0,1 } , F = { 0,1, { 0,1 } } . Функции f : E ” ^ E называются всюду определенными булевыми функциями ( P ₂ – множество всех всюду определенных булевых функций); f : E ” ^ F - ультрафункциями ( P~ - множество всех ультрафункций).

Пусть даны J ( x 1 ,...,x n ) e P ~ , f 1 ( x 1 ,...,x m ),..., f ” ( x 1 ,...,x m ) e P 2~ , тогда суперпозиция      f ( f ₁( x ₁,..., x_m ),..., f_n ( x ₁,..., x_m )) определяет функцию

g ( x ₁,..., x_m ) , принад-лежащую P ₂^~ , следующим образом [2]:

g ( « 1

а ) = < m

∩

f ( Д ,—, в _п ), если это пересечение не равно 0 ;

Pi ^е fi ( « ] ^,...^, «m )

и f ( Д ,- в ),

иначе.

. Pi^е fi ⁽ai^,...^,«m )

Функция f ( x 1 ,..., x n ): f ( a 1 ,..., a n ) = { a i } , где i е { 1,..., n } , называется селекторной.

Клон - множество функций, замкнутое относительно суперпозиции и содержащее все селекторные функции.

Интервалом I ( A , B ) называется частично упорядоченное по включению множество всех клонов, содержащих клон A и являющихся подмножествами клона B .

Интервалы представляются в виде диаграмм, где клоны изображаются точками и точка, представляющая клон A , расположена выше и соединена отрезком с точкой, представляющей клон B , если множество A непосредственно содержит B .

Если A - множество, то через [A] обозначим пересечение всех кло нов, содержащих A. Множество A называется полным, если [ A] = P2 .

Пусть K - клон, K , его подклон, тогда K 1 называется максимальным подклоном в K тогда и только тогда, когда [ K 1 u { f } J = K для любой f е K \ K 1 .

Определим множества:

T o,o = { f е P 2 I f (0,...,0) = 0 } , T o~ = { f е P | f (0,...,0) = 0 } ,

Ту ={ f е P2 | f (1,...,1) = 1 }, T1 ={ f е P; | f (1,...,1) = 1 }, m rT' rT' T1 ~    ~i~ ~i~

T 01 = T 0,0 ^ T 1,1 , T 01 = T 0,0 ^ T 1,1

Нетрудно проверить, что эти множества ультрафункций являются клонами.

В работе описан интервал I ( T ₀₁, P ₂ ~ ) и показано, что он содержит ровно 8 клонов из P ₂ ~ (включая сам этот клон).

В дальнейшем для удобства изложения будем использовать кодировку { 0,1 } ^ ~, а функции задавать в виде векторов-значений ультрафункций на всех наборах, расположенных в натуральном порядке.

• 1.    Некоторые полные множества

Приведем некоторые примеры полных множеств ультрафункций, на которые мы сошлемся при доказательстве теорем.

Пусть

h ( х ) = (~ 0), h ₂( х ) = (0 ~), h₃(x ) = (1~), h ₄( x ) = (~1), h₅ ( x ) = (~~), h ₆( x ) = (01), h ₇( x ) = (10), h ₈( x ) = (00), h ₉( x ) = (11), h _w( x i , x 2 ) = (0001), h _n( x i , x 2 ) = (0111), h i2 (x i ,x 2 )=(~~11), h 13 ( x 1 , x 2 ) = (~1~ 1), h _M( x 1 , x 2 ) = (~ 111), h 15 ( x 1 , x 2 ) = (00 ~~), h ₁₆ ( x 1 , x ₂ ) = (0 ~ 0 ~), h ₁₇ ( x 1 , x ₂ ) = (000 ~), h ₁₈ ( x 1 , x ₂ x ₃ ) = (01000011).

Замечание . Функции h ₆, h ₁₀, h _u, h ₁₈ принадлежат множеству T ₀₁, функции h ₁₂, h ₁₃ ( h ₁₅, h ₁₆) можно получить суперпозициями из h ₄ ( h ₂) и селекторных функций и [ { h ₁₀, h ₇ } ] = P₂ , [ P ₂ u { h ₅ } ] = P ₂ ~ .

Лемма 1. Множество функций T ₀₁ u { h 1 } является полным в P ₂ ~ .

Доказательство. Построим последовательность суперпозиций, задающую ультрафункции из [ T ₀₁ u { h 1 } ] и содержащую ультрафункции h ₅ и h ₇ :

^h 10 ^{( h} 1 , ^h 6 ) = ^ ^h 1 ⁽ h i) = ^h 5 , ^h 11 ^{( h} 1 , ^h 6 ) = ^h 4 , ^h 11 ^{( h} 12 , h 13 ) = h 14 , h ₁₄( h ₅, h ₅) = h ₉, h ₁₈( h₈,h ₆, h ₉) = h ₇.

Лемма 2. Множество функций T ₀₁ u { h₃ } является полным в P ₂ ~ .

Доказательство. Цепочка суперпозиций hw(h3,h6) = h2,hn(h3,h6) = hq,h2(h9) = h5,hw(h15,h16) = h17,h17(h5,h5) = hi, h18(h8, h6, h9) = h7 содержит ультрафункции h5 и h7.

Следствие 1. Множество ультрафункций T0,0 и{h1} и T,1 и{h3} яв ляется полным в P2~ .

Лемма 3. Множество функций T ₀₁ и { h ₅ } является полным в P ₂ ~ .

Доказательство.     h 11 ( h ₆, h ₅) = h ₄, h 11 ( h ₁₂, h ₁₃) = h ₁₄,    h ₁₄( h ₅, h ₅) = h 9 ,

• ^h 10 ^{( h} 5 , ^h 6 ) = ^h 2 , ^h 10 ^{( h} 15 , ^h 16 ) = h 17 , ^h17 ^{( h} 5 , Ю = ^h 8 , ^h 18 ⁽ h i , ^h 6 , ^h9 ) = ^h 7 •

Следствие 2. Множество функций T ₀ , ₀ u { h ₅ } и T ,1 u { h ₅ } является полным в P ₂^~ .

Основной результат

Теорема 1. Клоны, представленные на рис. 1, различны и вложены друг в друга так, как показано на рисунке.

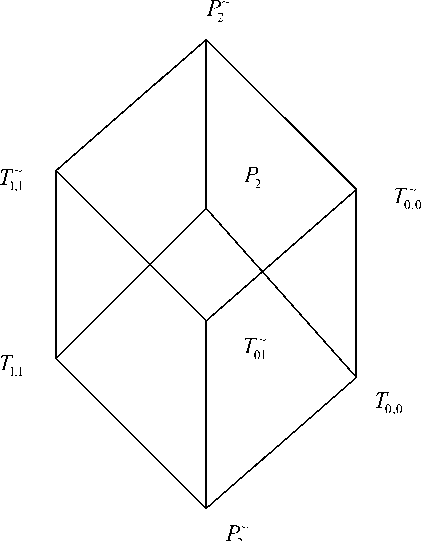
Рис. 1. Интервал I ( T ₀₁, Р₂)

Доказательство. Достаточно легко проверяется несовпадение указанных клонов, остается проверить их структуру вложенности. В [2] доказано, что T ₀₁ является максимальным подклоном в T₀₀ и T 1 , а также то, что Т _{0 0} и T 1 являются максимальными в Р₂ , в [4] то, что Т _{0 0} - максимальный подклон в T ₀ ~ ₀ и T .. максимальный подклон в Т ~ , в [3] то, что T ₀ ~ ₀ и Т ~ - максимальные поклоны в Р ₂ ~ .

Остается показать, что T ₀₁ является максимальным подклоном в T ₀ ~ , и T ₀ ~ - максимальный подклон в T ₀ ~ ₀ и Т ~ .

Сначала докажем, что выполняется равенство [ T ₀₁ u { f } ] = T ₀ ~ , где f ⁽ x p-> x n ) ^e T V T 01 .

Доказательство включения [ T ₀₁ u { f } ] с T ₀ ~ очевидно.

g( a - ,..., a ; ) = 0; g( в ,..., A m ) = 1; g( Y t ,..., Y m ) = ~.

Так как функция f ( x ₁,..., x_n ) е T ₀ ~ / T ₀₁, то f (0,...,0) = 0, f (1,...,1) = 1 и пусть ( T 1 ,. .., T _n ) такой набор, что f ( т 1 ,..., т _п ) = ~.

Возьмем функции    h1(x1,...,xm),...,hn(x1,...,xm)е T01    такие,    что h, (0,...,0) = 0, h,(1,...,1) = 1, h/a/,...,am) = 0, h^,...,0m) = 1, hY,...,Ym) = T,где iе {1,...,n}, je {1,...,r} , kе {1,...,s}, lе {1,...,t}.

Пусть суперпозиция f ( h 1 ( x 1 ,..., x m ),..., h_n ( x 1 ,..., x m )) определяет функцию ф (x 1 ,...,x m ). Покажем, что ф ( x 1 ,..., x m ) = g ( x 1 ,..., x m ).

Действительно,

ф (0,...,0) = f ( h 1 (0,...,0),..., h n (0,...,0)) = f (0,...,0) = 0,

ф (1,...,1) = f ( h 1 (1,...,1),..., h n (1,...,1)) = f (1,...,1) = 1, jj   jj  jj

^{ф ( а} 1 ,..., ^a m ) ^{j (,}4^{( a} 1 ,..., ^a m ),..., ¹ Пг ^{( a} 1 ,^..., ^a m ⁾⁾ J ⁽'-',...,'-') ф ( в ,..., e m ) = f ( h 1 ( A 1 k ,..., в ),..., h n в ,..., в )) = f (1,...,1) = 1, ФY x ,..., Y m ) = f ( h 1 ( Y 1 ,..., Y m ),..., h n ( Y ,..., Y m )) = f ( Т р- Т , ) = ~, i е { 1,..., n } , y е { 1,..., r } , k е { 1,...,s } , l е { 1,..., t } .

Отсюда следует, что g ( x 1 ,..., x_m ) е [ T ₀₁ u { f } ] , т.е. выполняется включение T ₀ ~ с [ T ₀₁ u { f } ] . Таким образом, доказали справедливость равенства [ ^T 01 -' ! ^f } ] = ^T 0~ .

Следующим шагом покажем, что выполняется равенство [ Т ,~ и { f } ] = T ,~0 , где f ( x 1 ,..., x , )е ^ / T 0~ .

Доказательство включения [ T ₀ ~ u { f } ] с T ₀ ~ ₀ очевидно. Если f ( x 1 ,..., x , ) е T 0~0 / T 0~ , то f (0,...,0) = 0 и f (1,...,1) = 0 или f (1,...,1) = ~. В любом случае имеем (00) е [{ f }]. Теперь функцию g ( x ₂,..., x_m ) из T ₀ ~ ₀ можно представить суперпозицией g ( x ₂,..., x_m ) = h (0, x ₂,..., x_m ), где h ( x 1 ,..., x_m ) - подходящая функция из клона T ₀ ~ .

Аналогично доказывается, что выполняется равенство ^{[ T} 0~ ^u{ ^f } ] = ^T ~1 , где ^{f ( x} 1 ^,...^{, x}n ) ^{е T} ~1 / ^T 0~ .

Теорема 2. В множестве P ₂ ~ существуют ровно 8 клонов, содержащих клон T₀₁, а именно клоны, представленные на рис. 1.

Доказательство. Пусть A - клон в P ₂ ~ такой, что T ₀₁ с A с P ₂ ~ . То, что нет клонов между Р ₂ и P ₂ ~ показано в [2]. Если A / T ₀₁ = 0 , то A = T ₀₁. В противном случае выполняется одно из следующих условий:

• 1.    Существует функция f е A такая, что f (0,...,0) = 1, f (1,...,1) = 0. Тогда получим Р ₂ с A .

• 2.    Существует функция f е A такая, что f (0,...,0) = 0, f (1,...,1) = 0 и не существует набора ( a _p..., a n ) такого, что f( a 1 ,..., a n ) = ~. Тогда ^T 0,0 ^с A .

• 3.    Существует функция f е A такая, что f (0,...,0) = 1, f (1,...,1) = 1 и не существует набора ( a 1 ,..., a n ) такого, что f ( a 1 ,..., a n ) = ~. Тогда T 1 с A . Аналогично показывается, что если A Ф Т ~ и A Ф Р ₂, то, используя следствие 1 и следствие 2, получим A = P ₂^~ .

• 4.    Существует функция f е A такая, что f (0,...,0) = 0, f (1,...,1) = 1 и существует набор ( a 1 ,..., a n ) такой, что f ( a 1 ,..., a n ) = ~. Тогда T ₀ ~ с A . Пусть A Ф T ₀ ~ ₀ и A Ф T ~ . Тогда в A существует либо функция h ₇, либо h ₃, либо h ₁ , либо h ₅ . В первом случае получим P ₂ с A . В остальных случаях, используя соответственно лемму 1, лемму 2 и лемму 3, получим A = P ₂ ~ .

• 5.    Существует функция f е A такая, что f (0,...,0) = 0, f (1,...,1) Ф 1, и существует набор ( a 1 ,..., a n ) такой, что f ( a 1 ,..., a n ) = ~. Тогда T ₀ ~ ₀ с A . Получим A = P ₂ ~ или A = T ₀ ~ ₀.

• 6.    Существует функция f е A такая, что f (0,...,0) Ф 0, f (1,...,1) = 1, и существует набор ( a 1 ,..., a n ) такой, что f ( a 1 ,..., a n ) = ~. Тогда T ~ с A . Получим A = P ~ или A = T ~1 .

• 7.    Существует функция f е A такая, что f (0,...,0) = ~, f (1,...,1) = 0. По лемме 1 получим A = P ₂^~ .

• 8.    Существует функция f е A такая, что f (0,...,0) = 1, f (1,...,1) = ~. По лемме 2 получим A = P ₂ ~ .

• 9.    Существует функция f е A такая, что f (0,...,0) = ~, f (1,...,1) = ~. По лемме 3 получим A = P ₂ ~ .

Пусть A Ф T _{0 0}, A Ф T ₀ ~ ₀ и A Ф Р ₂. Рассмотрим 2 возможных случая. В первом случае в A существует функция f ( x 1 ,...,x n ) такая, что f (0,...,0) = 1 и на некотором наборе ( a 1 ,..., a n )| f( a 1 ,..., a n ) = ~. По следствию 1 получим A = P ₂ ~ . Во втором случае в A существует функция f ( x 1 ,..., x n ) такая, что f (0,...,0) = ~. Тогда легко получить функцию h ₅, и по следствию 2 имеем A = P ₂ ~ .

Цыренова В.Б., Батожаргалова А.Э. Линейчатые поверхности с параболическими образующими в четырехмерном квазиэллиптическом пространстве