О локальных бифуркациях дифференциальных уравнений второго порядка с кусочно-гладкой правой частью

Бифуркации положений равновесия в типичных однопараметрических и двухпараметрических семействах кусочно-гладких динамических систем на плоскости, при которых рождаются периодические траектории, в основном описаны [1–6]. Естественно исследовать такие бифуркации и в более узких классах кусочно-гладких динамических систем, представляющих интерес для приложений.

Будем рассматривать семейство дифференциальных уравнений второго порядка fp : x = f (x, x, Ц), зависящих от n -мерного параметра ц, и соответствующее семейство динамических систем x = У, y = f(x, y, ц),                          (1)

которые также будем обозначать f . Будем предполагать, что f ( x , у , ц ) определена в некоторой окрестности ( - 1 , 1 )² х ( - ц , ц ) n нуля в пространстве R ² х R ⁿ переменных ( x , у , ц ), а фазовое пространство Ф = ( - 1 , 1 )² разбивается линией 5 : у = 0 на множества Ф + : {( x , у ) еФ : у >  0} и Ф _ :{( x , у ) еФ : у <  0}. На множестве Ф ± х ( - ц , ц ) n функция f совпадает с C -функцией f ± , определенной на ( - 1 , 1 )² х ( - ц , ц ) n ( r >  2).

В точках ( x 0 ,0) е 5 , где f - ( x 0 ,0,0) f + ( x 0 ,0,0) <  0 траектории динамических систем f _ц «сшиваются» из дуг траекторий динамических систем f p ^: x = у , у = f ± ( x , у ,0), ( x , у ) еФ ± , и являются C ¹ -гладкими. В точках ( x ₀,0) е 5 , где f - ( x ₀,0,0) f + ( x ₀,0,0) >  0 , будем использовать выпуклое доопределение на 5 [1, с. 95]. Поскольку вектор из выпуклой оболочки векторов (0, f ± ( x ₀,0,0)), касательный к 5 , является нулевым, то точку ( x ₀,0) будем считать целой траекторией — положением равновесия.

Опишем бифуркации в окрестности особой точки (0,0) еФ в «типичных» семействах уравнений, зависящих от одного и двух параметров, при которых рождаются предельные циклы.

Вследствие (2)-(3) дуга S между точками O - ( ц ) и O + ( ц ) состоит из положений равновесия, устойчивых при x ₊ ( ц ) <  x - ( ц ) и неустойчивых при x - ( ц ) <  x ₊ ( ц ).

При достаточно малом р0> 0 найдется такое ц'е (0, ц,), что Vце (-ц',ц')n x±(ц) е (-р0,р0), а положительная (отрицательная) полутраектория системы /ц (f- ), начинающаяся в точке (р, 0) е S, ре[-р0,р0], следующий раз пересекает S в точке (g + (р,ц),0) ((g- (р, ц),0)), где g±е Cr, (g±)р (р, ц) < 0, g± (x± (ц), ц) = x± (ц) [7, с. 252]. Пусть g-’(•, ц) — функция, обратная к функции g- (•, ц). Введем функ- цию d(р,ц):= g + (р,ц) - g-(р,ц), (р,ц) е (-р0,р0) х(-ц',ц')n.

Мы можем выбрать р 0 е (0, р0 ] и 50 е (0, ц'] так, чтобы ^це (-50,80) n x ± (ц) е (- р0, р0), g + (р, ц) е (- р 0, р0), если ре (- р0, р0). Тогда функция P (•, ц ):= g:’(g + (•, ц), ц), определенная на отрезке [-р0, x (ц)], где x(ц) := min{x + (ц),x-(ц)}, является функцией последования по траекториям системы /ц . Пусть р, е (-р0, x(ц)) — неподвижная точка функции последования: P(р,, ц) = р,. Тогда через точку S с координатой x = р, проходит замкнутая траектория уравнения /ц . При рр(р,, ц) < 1 (Рр(р,, ц) > 1) эта траектория является устойчивым (неустойчивым) ги- перболическим предельным циклом, а при рр( р,, ц) = 1,

Р рр ( р , , ц ) * 0 — двойным циклом. Так как

P ⁽ р , ц ) = g ^{- 1 (} g + ⁽ р , ц ), ц ), P ⁽ р , ц ) =—( т у- р ^- т-т, ⁽ g - ) р ⁽ P ⁽ р , ц X ц )

р рр ( р , ц ) =

⁽ g + ) "рр ⁽ р , ц ) ⁽ g - ) р ⁽ Р , ц )

⁽ g + ) р ⁽ р , ц ⁾⁽ g - ) "р ⁽ р ), ц ) ^р' р ⁽ р , ц )

[( g - ) р ( р ), ц )]²           J р = P ⁽ р , ц )’

P ( р , , ц ) = р , , р р ( р , , ц ) <  1( > 1) . . d ( р , , ц ) = 0, d р ( р , , ц ) >  0( < 0), (4) ^р р ⁽ р , , ц ) = ⁽ g + ) р ⁽ р , , ц ^)/( g - ) р ⁽ р , , ц ) = ¹ ^ ^d ; ⁽ р , , ц ) = ⁰,

^{р (} р , , ц ) = р , , ^р р ⁽ р , , ц ) = 1, ^р рр ⁽ р , , ц ) * ⁰ ^                             (₅)

о d ( р , , ц ) = d ; ( р , , ц ) = 0, d' Р; ( р , , ц ) * 0.

Обратно, если замкнутая траектория системы / ц пересекается с дугой ( - р ₀, р ₀) х {0} с S , то она проходит через точку с координатой x = р , е ( - р 0 , x ( ц )), а P ( р , , ц ) = р , .

Если d р (0,0) = ... = d ^ (0,0) = 0, ( - 1) k d ^\ ^}(0,0) <  0, к = 1,..., r , то все траектории уравнения f _}, начинающиеся в достаточно малой окрестности точки O , го -предельны ( а -предельны) к O . В этом случае точку O будем называть устойчивым (неустойчивым) фокус-фокусом системы f ₀ кратности k .

Из [7, с. 100-101] следует, что

( g + ) р ( х + ( ц ), ц ) = - e a ^{( ц )/ в+ ( ц} ) , ( g - ) р ( х - ( ц ), Н ) = - е ^{п ( ц} > ^{/ в- ( ц} ) .   (6)

Поэтому dP(0,0) = е"”“-(0)/в— (0)(1 -епЛ(0)).                         (7)

• 2 Бифуркации особой точки типа фокус-фокус в однопараметрическом семействе

Здесь будем рассматривать однопараметрическое семейство f µ , ц е ( - ц , ц ) систем вида (1), где f ± е C r , r >  2 .

Теорема 1. Пусть точка O = (0,0) — фокус-фокус системы f , и Л (0) <  0 , Д‘ (0) >  0 . Тогда существуют окрестность U точки O с C ¹ -гладкой границей д U и число ц ₀ е (0, ц ) такие, что (рис. 1)

для любого це ( - ц ₀, ц ₀) траектории систем f _ц в точках д U входят вU;

при це ( - ц ₀,0) f _ц имеет в U единственную замкнутую траекторию, являющуюся устойчивым грубым предельным циклом, к которому ω -предельны все остальные траектории, начинающиеся в U и отличные от положений равновесия на отрезке [O - ( ц ) O ₊ ( ц )] ;

при ц = 0 все траектории системы f _ц , начинающиеся в U \ O, ω -предельны к O ;

при це (0, ц ₀) все траектории системы f _ц , начинающиеся в U, кончаются в одном из положений равновесия на отрезке [ O ₊ ( ц ) O - ( ц )] .

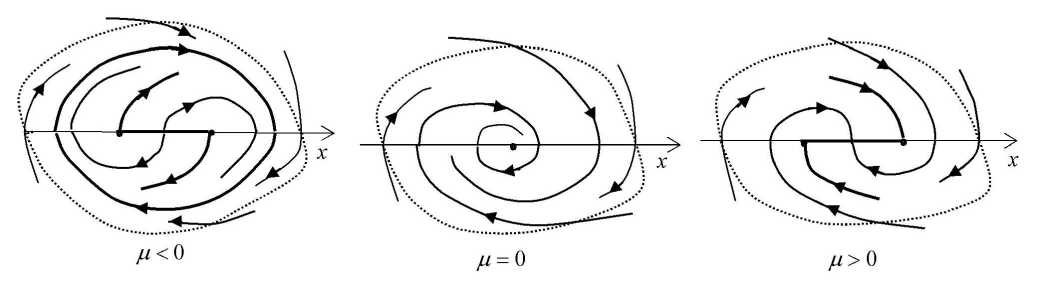
Рис. 1. Бифуркации в однопараметрическом семействе

Доказательство. Так как Л(0) < 0, то из (7) следует, что d'p (0,0) > 0,(8)

Поэтому числа р ₀ и р ₀ можно считать выбранными так, что

P(р,0) > р для всех р е [-ро,0),(9)

d'p (р, р) > 0 для всех - Р0 < р < x (р), ре (-Р0, Р0),(10)

Из (9) и [8, с. 100] следует, что через точку S с координатой x = P ( - р ₀,0) можно провести замкнутую C ¹ -кривую у , в точках которой траектории системы f , трансверсальны у и направлены внутрь области U э O , ограниченной у . При достаточно малом р ₀ траектории системы f _p , ре ( - р ₀, р ₀), в точках у = д U также направлены внутрь U , а замкнутая траектория принадлежит U тогда и только тогда, когда она пересекается с дугой S _р : - р ₀ <  x <  x ( р ) линии переключения S .

Из (9) теперь следует, что все траектории системы f , , начинающиеся в U \ O , to -предельны к O .

Из равенства d(0,0) = 0 и (8) получаем, что р0 и р0 можно взять такими, что d (-р0, р) < 0 для всех ре (-р0, р0).                  (11)

Поскольку А‘ (0) >  0, то можно считать, что V р е (0, р ₀) x + ( р ) >  x _ ( р ) и d ( x _ ( р ), р ) = g + ( x _ ( р ), р ) - x _ ( р ) >  x + ( р ) - x _ ( р ) >  0 .       (12)

Из (10)-(12) следует, что при ре (0, р ₀) d ( • , р ) имеет единственный нуль р , ( р ), при этом d p ( р , ( р ), р ) >  0. Ввиду (4) P ( • , р ) имеет единственную, причем устойчивую неподвижную точку р , ( р ), а система f имеет единственную (устойчивую) замкнутую траекторию в U .

При ре (-р0,0) x + (р) < x _ (р) и d(x + (р), р) = x + (р) - g_(x + (р), р) < x + (р) - x_(р) < 0 .      (13)

Из (10), (11) и (13) следует, что при ре ( - р ₀,0) d ( • , р ) не имеет нулей. Соответственно, система f не имеет замкнутых траекторий в U .

Пусть выполняется и условие

Л ' , (0) д ^ 2 <0) -Л ' 2 (0) Д ^ ₁(0) * 0.

Тогда, сделав замену параметров Д’ = Л ( д ₁, д ₂), д 2 = ^ ( Д о H ₂) и вернувшись к их прежним обозначениям, можно считать

^{Л (} H i , H 2 ) = H i , Л ⁽ H i , H z ) = H 2 .                        ⁽¹⁴⁾

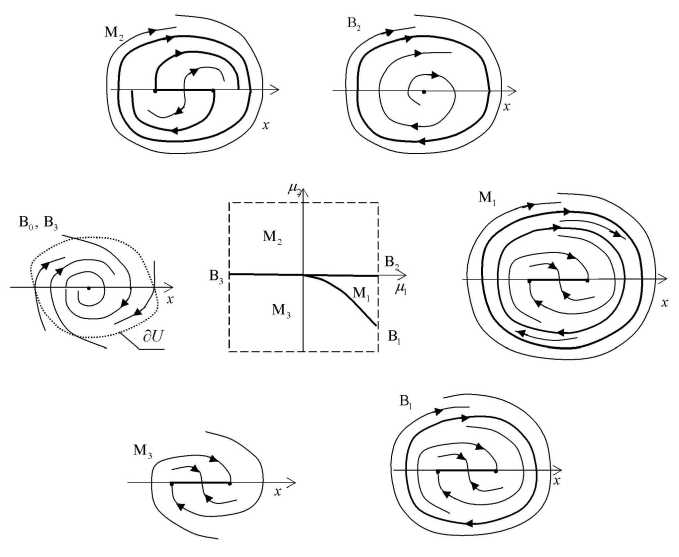
Рис. 2. Бифуркации в двухпараметрическом семействе

Теорема 2. Пусть точка O = (0,0)— устойчивый фокус-фокус уравнения f ₀ кратности два , а параметры ( д ₁, Д ₂) выбраны так, что выполняются равенства (14). Тогда существуют окрестность U точки O с C¹ -гладкой границей д U, число 5 е (0, д ) и разбиение области параметров ( -5 , 5 )² на множества

В _о = {0} , B 1 = { д : Д 2 = в ( H i ), в е C 4(0, 5 ),( - 5 ,0)), в ( + 0) = в ‘ ( + 0) = 0} ,

B 2 = (0, 5 ) х {0} , B 3 = ( - 5 ,0) х {0} , M i = { д : в ( H i ) <  Д 2 <  0} , M ₂ = ( - 5 , 5 ) х (0, 5 ) , M ₃ = { д : -5 <  д ₂ <  в ( д ₁)} и ( - 5 ,0] х ( - 5 ,0) со следующими свойствами (рис. 2):

Для любого д е ( - 5 , 5 )² траектории f _H в точках д U входят в U.

Система f _д , де ( - 5 , 5 )² , имеет в U следующие особые точки: устойчивый (неустойчивый) фокус-фокус при д е В ₀ иВ ₃ ( д еВ ₂ ); отрезок [ O - ( д ) O ₊ ( д )] из устойчивых (неустойчивых) положений равновесия при д е В ₁ и М ₁ иМ ₃ (при д еМ ₂ );

Система f _p , це ( - 8 , 8 )² , имеет в U следующие замкнутые траектории: двойной цикл при ц еВ 1 , устойчивый и неустойчивый гиперболические предельные циклы при ц еМ , , устойчивый гиперболический предельный цикл при ц е В ₂ иМ ₂ .

Доказательство. Представим d(р,ц), (р,ц) е (-р0,р0) х (-80,80)2 в виде d(р, ц) = x + (ц) + a + (р, ц)(р - x + (ц)) -x_ (ц) - a_(р, ц)(р - x_(ц)), где a± — C-1 -функции, а ± (x ± (ц), ц) = (g ± )р (x ± (ц), ц), (15) и сделаем замену и = р - x_ (ц). Функция d(р, ц) преобразуется в функ- цию d (и, ц) := d(x- (ц) + и, ц) = ц2 + а+(x + (ц) + и - ц2, ц)(и - ц2) -

• - а - ( x - ( ц ) + и , ц ) и .

Из этого равенства, учитывая (15), (6) и (14), получаем

d(и,ц) = ц2(1 - а + (0,0) + q(и,ц)) + b(ц)и + r2(и,ц),(16)

d и(и, ц) = b(ц)+(r-X(и, ц), где q е C1 и r2 е Cr,

q(0,0) = 0, r2(0,ц) = (r /(0,ц) = 0, (r^(0,0) = d^(0,0) <0,(18)

а b ( ц ) = e™™ ( ц Ув- ( ц) - e™a ( ц Ув+ ( ц) = e™- ( ц У Д- ( ц )(1 - enA( ц))

Так как Л ( ц ) = ц 1 , то

b(ц) = ц Ь1(ц), где Ъ1(-) е C 1, b1(0)< 0.(19)

Поскольку а + (0,0) = (g + )р (0,0) < 0, то 1 - а + (0,0) > 0, из (16) и (18) следует, что числа р0 и 80 можно считать выбранными так, что d 'цг (и, ц) > 0 при всех це (-80,80)2, - р0 - x - (ц) < и < min{0, ц2}. (20) Так как d. (0,0) = d.и (0,0) = 0, а из (16)-(20) имеем d и'щ(0,0) d ц1(0,0)

d и ц ₂(0,0) d ц ₂(0,0)

b 1 (0)    q'_u (0,0)

0     d ц 2 (0,0)

* 0,

то по теореме о неявной функции существуют такие числа 8 1 е (0, 8 ₀) и

0 <  и <  р - max | x ( ц )| , что для и е [ - и , и ] система уравнений ц е ( - 8 1 , 8 1 )²

d. ( и , ц ) = d. '_и ( и , ц ) = 0

имеет относительно ц = (ц1, ц2) е (-81,81)2 единственное решение ц1 = тх(и) , ц2 = m2(и) ; при этом mj(-),m2(-) е C2,

m(и ) = - [(< „ (0,0)/ 6 1 (0)] и + o ( и ) ,               (21)

m ₂( и ) = [0,5( r ₂>"(0,0)/(1 - а ₊ (0,0))] и ² + о ( и ²) .         (22)

Чтобы р = x _- ( ц ) + и было неподвижной точкой функции последования P ( • , ц ) при ц 1 = m 1 ( и ) , ц ₂ = m ₂( и ) , должно выполняться неравенство и <  min{ m ₂( и ),0} . Поскольку 6 1 (0) <  0, (г)" (0,0) <  0, 1 - а ₊ (0,0) >  0 , то из (21) и (22) следует, что и можно считать столь малым, что при всех и е [ - й , 0] m ‘ ( и ) <  0 , а при и е [ - и , 0) m , ( и ) >  0 , и <  m ₂( и ) <  0 .

Функция m , ( и ) , и е [ - и , 0] , имеет обратную m ₁ - ¹( ц 1 ) , ц 1 е [0, 5 ₂] , где 5 ₂ = m , ( - и ) . Обозначим в ( Ц 1 ) : = m ₂( m -V Ц 1 )) • Считая й достаточно малым, из (21) и (22) будем иметь - ц , <  в ( Ц 1 ) <  0 для всех ц е (0, 5 2 ] и в (0) = в ' (0) = 0 .

Так как й' Р_р (0,0) <  0, то и и 5 е (0, 5 ₂) можно выбрать так, что

Й ии ( и , ц ) <  0 для - й <  и <  0, це ( - 5 , 5 )².                  (23)

Отсюда и из равенств Й (0,0) = Й и (0,0) = 0 следует, что Й ( й ,0) <  0. Поэтому при фиксированном й число 5 можно выбрать столь малым, что

Й ( й , ц ) <  0 при всех це ( - 5 , 5 )² .             (24)

Из (16) и (18) следует, что 5 можно считать таким, что

Й (0, ц ) >  0( = 0) при це ( - 5 , 5 ) х (0, 5 ) (при це ( - 5 , 5 ) х {0} ). (25) Для и = ц ₂ из (16) получаем

Й ( ц 2 , ц ) = ц 2 (1 - а + (0,0) + q ( ц ₂, ц ) + 6 ( ц ) ц ) + r ₂ ( ц ₂, ц ).

Ввиду (18) r ₂( ц ₂, ц ) = о ( ц ₂) равномерно относительно ц 1 . Следовательно, 5 можно считать выбранным столь малым, что

Й ( ц ₂, ц ) <  0 при всех ц = ( ц 1 , ц ₂) е (0, 5 ) х ( - 5 ,0) .       (26)

Через точку 5 с координатой x = P ( - й ,0) проведем C ¹ -гладкую замкнутую кривую у , трансверсальную траекториям уравнения f , и ограничивающую окрестность U точки O . Если 5 достаточно мало, то Y — трансверсаль и для траекторий уравнения f _p , ц =е ( - 5 , 5 )² , а замкнутая траектория принадлежит U тогда и только тогда, когда пересекает дугу 5 _ц : - й + x - ( ц ) <  x <  min{0, ц ₂} + x - ( ц ) линии 5 .

Определим множества B i , M j так, как это описано в формулировке теоремы 2. Учитывая (23) и (5), получаем, что при ц еВ 1 дугу 5 _ц пересекает двойной цикл, а при остальных ц е ( - 5 , 5 )² эту дугу могут пересекать только гиперболические замкнутые траектории.

Так как при ц еВ , d ( m /( ц , ), ц ) = d U ( m /( ц , ), ц ) = 0, а d"_и ( и , ц ) <  0 при всех u е [ - й , 0] , то d ( и, ц ) <  0, если u * m ^{- 1}( ц , ). Тем самым при ц еВ , двойной цикл — единственная замкнутая траектория, пересекающая дугу S _ц .

Вследствие (20)

d ( m , ( ц , ), ц ) >  0 при ц еМ , „В . .

Из (24), (26), (27) и (23) получаем, что при любом ц еМ , существует точка й е ( - и , ц ₂) такая, что d ( ua, ц ) >  0, d U ( и , ц ) >  0 при и е ( - й , U ) и d U ( и , ц ) <  0 при и e ( U, ц ₂). Поэтому d ( • , ц ) имеет один нуль на ( - й , U ) и один нуль на ( U, ц ₂). Вследствие (4) дугу S _ц пересекают два гиперболических предельных цикла, устойчивый и неустойчивый.

Если ц принадлежит В ₂ или М ₂, то из (24) - (27) и (23) получаем, что d ( • , ц ) имеет на ( - й ,0) единственный нуль и , , причем d U ( и , , ц ) >  0. Вследствие (4) дугу S - пересекает единственная замкнутая траектория — устойчивый гиперболический предельный цикл.

Если ц е (0,5), -5 < ц2 < вАц,), то ввиду (20) для любого и е [-й, 0] d(и,(ц,, ц2)) < d(и, ц,, в,( ц,)) ^ 0. Вследствие (24), (25) и простоты нулей d (•, ц) число нулей d (•, ц) на (-й,0) — локально постоянная функция на М3. В силу связности М3 число нулей d (•, ц) на (-й,0) постоянно при всех цеМ3. Поскольку d (•, ц) не имеет нулей при ц, е (0,5) , -5 < ц2 < в,(ц,), то их нет и при всех ц еМ3. Соответ ственно, замкнутые траектории не пересекаются с дугой Sц .

Покажем, что при ц еВ ₃ замкнутые траектории также не пересекаются с дугой S _ц . Предположим, что это не так. Тогда d ( • , ц ) имеет на ( - й ,0) простой нуль. Но тогда при ц еМ ₃ и достаточно близких к ц , d. ( • , / /) тоже имеет на ( - й ,0) нуль, что невозможно. Поэтому сделанное предположение неверно и замкнутые траектории не пересекаются с S ^ .

Заключение

В работе рассмотрены семейства динамических систем на фазовой плоскости, задаваемые дифференциальными уравнениями второго порядка x = f ( x , x , ц ) с правыми частями, разрывными на линии х = 0 и зависящими от одномерного или двумерного параметра ц . В случае «общего положения» описаны бифуркационные диаграммы таких семейств, что при нулевом значении параметра система имеет устойчивое положение равновесия типа фокус-фокус. В частности, указаны области значений параметра, при которых из положения равновесия рождается устойчивый предельный цикл. Полученные результаты могут быть использованы для описания возникновения автоколебаний в реальных релейных системах управления.