О матричной краевой задаче Римана в аналитическом решении граничных задач теории газов

Одним из важнейших при решении граничных задач кинетической теории газа, теории переноса, является метод, часто называемый [1] методом Кейза. Предложенный в 1960 году [2] в работе о переносе нейтронов, уже через два года он был развит и применен К. Черчиньяни [3] в решении граничной задачи для линеаризованного уравнения Больцмана с интегралом столкновений в форме Бхатнагара — Гросса — Крука (БГК). Сформулированная идеология позволила получать удобные результаты в части разработки новых методов аппроксимации и строить единую теорию получения аналитических решений граничных задач. При этом в зависимости от используемой модели задача сводится к исследованию как скалярных, так и векторно-матричных интегро-дифференциальных уравнений различного вида [4] – [6] . Центральным звеном аналитического решения матрично-векторных граничных задач такого вида является решение матричной краевой задачи Римана, сложность исследования которой в значительной степени и определяет сложность применения метода в целом. Обзор вопроса с акцентом на решение конкретных физических задач дан в работе [1] А. В. Латышева и А. А. Юшканова, однако более общий подход [7] с опорой на работы [8] – [9] позволяет обобщить предлагаемую методику на более широкий класс уравнений.

1 Подводящие соображения

Рассмотрим граничную задачу для уравнения относительно неизвестной двухкомпонентной вектор-функции Y (x, ^)

p^Y(x,p) + Y(x,p') = -1=Q(p) [ Qi(p')Y(х,^е ^' dp, (1) ∂x                 π -∞ где Q(p) и Qi(p) — полиномиальные матрицы-функции, а решение ищется в классе функций, непрерывных по x на множестве 0 < x < +от при всех µ ∈ R , непрерывно дифференцируемых по x на множестве 0 < x < +го при всех p 6 R , гельдеровых по p на промежутке [0, +го] при всех 0 < x < +то. Граничные условия установим в виде:

Y ^{(0 ,}Р) = ^Y 0 ⁽ P),P >  ⁰ ,

Y(x,p) = Yas(x,p),x ^ ^,p < 0, где Yo(p) — произвольная вектор-функция, удовлетворяющая условию Гельдера, а Yas(x,p) - линейная комбинация частных решений.

Граничные задачи такого вида возникают при рассмотрении задач кинетической теории газа и плазмы (в частности, задачи Смолуховско-го для уравнения с интегралом столкновения в форме Бхатнагара —

Гросса — Крука). Например, случай одно-, двух- и многоатомного газа описывается уравнением с матрицами

Q№ =

'Y(^ 2 - 1/2) ^γ

,Q i (^) =

' Y(^ 2 — 1/2)

lγ

(соответственно, l = 1,l = 2 и l = 5/2), причем y = \/2/(1 + 2l). Далее в работе будем называть перечисленные задачи частным случаем общей задачи. Разделяя переменные в (1) с помощью анзаца Кейза [2]

- ^x

Yn (x,V) = e n Ф (П, ^), где параметр η ∈ C , придем к характеристическому уравнению

(П - №(n, ^) =     nQ(^)n(n),^ € R , n € C . (2)

π

Момент нулевого порядка

n

∞

∞

e ^ 2 Q i (^) Ф (n,^) d^

представляет собой нормирующую вектор-функцию. Собственные функции Ф(п, ^) будем искать как в классе гельдеровых функций - к ним будут относиться

^Ф (П 0 ,Д) =

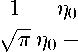
- Q(^)n(no) = F (По,^)п(По), µ соответствующие собственным значениям дискретного спектра η0 , вообще говоря, комплексным, так и в пространстве обобщенных функций

Ф(П,^) = F (n,^) n (n) , где матрица-функция

F ⁽ n,v)

= 7= nP—

-^Q M + B ⁽ n) 5 ⁽ n ^- ^) ^µ

есть собственная матрица непрерывного спектра, B(n) — некоторая гельдерова матрица-функция, а под P _x ¹ понимается главное значение интеграла по Коши от x ^-1 [8] . Матрица B(n) определяется условием нормировки:

B(n) = ■Q i ^{- 1}(п)Л(п),П € C , (3)

где матрицу-функцию

Л(z) = I + -= Г e - Q ' Q ' dц, (4) π -∞ µ - z называют дисперсионной матрицей, а ее определитель A(z) — дисперсионной функцией задачи (здесь I — единичная матрица).

Таким образом, набор собственных функций характеристического уравнения (2) состоит из собственных функций дискретного спектра, определяемых матричными функциями F (n j , ц) и собственных функций непрерывного спектра, определяемых обобщенными матричными функциями F(n,^), П € (0, +^ю). Их свойства определяются свойствами дисперсионной матрицы Л(z) и дисперсионной функции A(z). Введя в рассмотрение вспомогательную функцию Черчиньяни [3]

A c (z) = 1 + 4  ” e^-1      ,

π -∞ µ - z сможем получить следующее представление и свойства дисперсионной матрицы [10]:

Свойство 1. Если deg (Q i (z) Q (z)) = 1, то Л (z) = A c (z) Q _i (z) Q (z).

Свойство 2. Если deg(Q i (z) Q (z)) > 2, то матрица-функция Л(z) представляется в виде:

Л (z) = Ac (z) Qi (z) Q (z) + Q2 (z), где Q2(z) - полиномиальная матрица и deg Q2(z) = deg (Qi (z) Q (z)) — 2.

Свойство 3. При переходе через действительную ось матрица-функция Л (z) претерпевает разрыв. Ее граничные значения при приближении «сверху» и «снизу» (т.е. при z ^ ц + 0 • i и при z ^ ц — 0 • i, где ц € R ) соответственно равны:

Л ± (ц) = Л (ц) ± i — Пце ^-^² Q i (ц) Q (ц) , ц € R

Свойство 4. Поведение матрицы-функции Л(z) в окрестности бесконечно удаленной точки определяется рядом:

∞∞

Л(z) = I + Е z k -J ^ e  Q i   Q d^

Таким образом, необходимым и достаточным условием принадлежности бесконечно удаленной точки к дискретному спектру является равенство:

det I -[ e— Qi (ц) Q (ц) d^) = 0, π -∞ или, иначе, |Q1 (^)| • |Q (д)| — trQi (д) • Q (д) = 1. В рассматриваемом частном случае это следует из физических условий [7]:

Л(z) =

-

1 Г(5 + 2l)/(2 + 41)

z ²

1/^2 + 41

1/72 + 41 1/2

+ о

1 А z ²

, z -'X., ⁽⁵⁾

а дисперсионная функция A(z) = 4— 4 1++2 1 + о (44) , |z| — х. Последнее по сути означает, что в рассматриваемом частном случае бесконечно удаленная точка является четырехкратной точкой дискретного спектра.

В основе алгоритма построения решения граничной задачи для уравнения (1) лежит возможность разложения по собственным функциям граничных условий, то есть

Лемма 1. Для полноты системы собственных функций уравнения (2) { Ф( п, д), П € (0, +х); Ф (n j ,+)} в пространстве функций, гельде-ровых на отрезке [0, +х], достаточно, чтобы при д > 0 была разрешима неоднородная краевая задача Римана:

Л ⁺ ( _М ) X ⁺ ( _М ) — Л ^- ( _М ) X ^- ( _М ) = 2i V n^e - ^ 2 Q i (д) Y (д).

Доказательство. Полнота указанной системы функций означает возможность разложения по ним произвольной вектор-функции Y(д), удовлетворяющей условию Гельдера на замкнутой полуоси [0, +х], то есть

Y (д) = Y 1

∞ ы+

F ⁽п^,д⁾ a ⁽ n) dn,

где Y i (д) - линейная комбинация собственных функций дискретного спектра, a a (n) — коэффициент дискретного спектра. Домножим обе части равенства на де - Q l (д). Тогда с учетом выражения для F (n, д):

д - Q l (д)Y(д) = де^-2Qi^Y i^ ₊ -L д^ ² Q l (д)Q(д) Г ^dn+ π                ₀ η - µ

+Л(д)да(д), д > 0. (6)

Введя в рассмотрение вспомогательную вектор-функцию

\     1 Г° na (n) ,

N (z) = T? /0 n—7in’ определенную во всей комплексной плоскости с разрезом вдоль положительной действительной полуоси, и применяя к ней и к дисперсионной матрице Л(z) формулы Сохоцкого на полуоси (0, +х), можем записать:

N ⁺ (д)+ N ^-(д) =-7= [ ⁿ a^{( n )} in,N ⁺ (д) — N ^- (д) = 2 — П • iдa(д),

π ₀ η - µ

Л ⁺ (м)+Л (м)=2Л(м), Л ⁺ (м) - Л (^) = 2^П • ipe ^ Q i (м) Q (м), то есть в результате соотношение (6) перепишется в виде:

Л ⁺ (м) N ⁺ (м) - Л- (g) N- (м) + 2i^e- ^ 2 Q i (м) Y i (g) =

= 2i^n^e - ^' Qi(^)Y (м), или, иначе,

Л ⁺ (м) [ N +М + Q ^- WiM - Л-(^) [ N ^- (д)+ Q ^- W1M =

= 2i ^ n^e ^{- м} Q i (^)Y (м)м > 0.

Решение построенной краевой задачи Римана позволит определить коэффициенты непрерывного и дискретного спектра, что докажет возможность требуемого представления функции Y i (^). Лемма доказана.

2 Матричная задача Римана

Рассмотрим задачу: найти матрицу канонических решений X(z) [1] для краевой задачи, поставленной на берегах разреза (0, +го):

X+ Ы = Л+ Ы Л Ы]-1X-   , м > 0, то есть

[X ⁺ И^-1 Л ⁺ (м) = [X - М]^-1 Л-М , м> 0. (7)

Матрица Л(м) определена в предыдущем разделе, в частном случае зависит от положительного действительного параметра l. Матрица-функция G ( m ) = Л ⁺ (м) [Л ^- (м)] ^-1 называется матричным коэффициентом краевой задачи (7). Величина k ( G ) = ^ П [arg detG(^)] ( _{0 +} ^ ) , где под [f ] с понимается приращение функции f (z) при полном обходе кривой С в положительном направлении, называется индексом краевой задачи. Домножив (7) справа на Q ^{- 1} ( m ) Q ^{- 1} ( m ) и, обозначая

W (z)=Л(z)Q-1(z)Q-1(z), получим новую краевую задачу:

[X ⁺ (м)] - W ⁺ (м) = [X ^- (м)] ^-1 W ^- (м),м > 0.

Из свойств 1-2 можно получить представление W (z) в явном виде для случая, когда deg (Q ₁ (z) Q (z)) > 2:

W (z) = Ac (z) I + n(z), где n(z) = Q2(z)Q 1 (z)Q- 1(z). В частности, для задачи Смолуховского в случае одно-, двух- и многоатомного газов будем иметь:

^{n( z )}    2l [1/y

-^{Y ( z} 2 - l - ^{1 / 2)} 1/2 - z ²

Очевидно, что матричный коэффициент задачи (7)

G ( _M ) = Л + ( _M ) [Л " ( _M )] ^-1 = W + ( _M ) [W - M]^-1 .

Для диагонализации или приведения к жордановой нормальной форме матрицы-функции W(z) достаточно привести к такому виду n(z). Далее будем рассматривать случай, когда n(z) приводится к диагональному виду. Тогда диагонализирующая матрица S (z) существует и строится в явном виде, однако зависит от радикала r(z), что может порождать точки ветвления в конечной части комплексной плоскости. Очевидно, что точки ветвления, не лежащие на действительной оси, будут образовывать комплексно-сопряженные пары. В частном случае диагонализующая матрица-функция имеет вид:

S(z) =

■ 2 (z² + 2 + ф))

1/y

2 (z ² + 2 ^{- r (} z))’ 1/7

Тогда S ¹ (z)W(z)S(z) = Q(z) = diag {Q 1 (z), Q 2 (z)}, где Q _a (z) = A c (z) + 2 [ 2 - z ² + (-1) ^{a +1} r(z)] , a = 1, 2, r(z) = рф, q(z) = (z ² - 3/2) 2 + 4l. Матрица-функция S(z) является аналитической в комплексной плоскости за исключением точек ветвления радикала ±a, ±а (здесь a = p0.75 + 0.25ф~+ 16l + ip-0.75 + 0.25^9 + 16l), в которых функция r (z) обращается в нуль.

Заметим, что в общем случае r(z) = \Jq(z) является двузначной функцией, поэтому для однозначности S(z) выделим одну ветвь радикала [1] : для этого проведем в комплексной плоскости дополнительные разрезы, соединяющие попарно конечные точки ветвления, обозначим совокупность этих разрезов Г. В частном случае Г будет представлять собой пару отрезков, соединяющих точки ±a, ±а без пересечения с вещественной осью.

Лемма 2. Функция r(z) = ^q(z), z € С \Г такая что \J q(z o ) = г о , где r o = I \J q(z o ) I exp(iф o /2), а ф о есть главное значение аргумента q(zo'), является однозначной.

Доказательство. Положим, что γ есть простая замкнутая кривая с началом в точке z o , лежащая в С \Г. В результате обхода по 7 получаем значение ^q(z o ) = r o exp(iф/2), где ф = arg[(z -a)(z -a)(z + a)(z + a)] ? . При этом ф = ф 1 + Ф 2 + ф з + Ф 4 . Если разрезы Г 1 и Г 2 не лежат внутри

Y, то все фi =0, так что у/q(z o ) = г о . Если только Г 1 лежит внутри y , то в силу положительной ориентированности γ

Ф1 = ф4 = 2п, ф2 = фз = 0, так что ф = 4п и снова получаем \Jq(zo) = го. Аналогичные результаты получаются в случаях, когда внутри y оказывается Г2 или же сразу оба дополнительных разреза. Лемма доказана.

Решение задачи факторизации будем искать в виде

X (z) = S (z)U (z)S-1(z), причем S-1(z)W(z)S(z) = Q(z) = diag {Q1(z), ^(z)}. В частном случае Qa(z) = Ac(z) + 41 [2 — z2 + ( —1)a+1r(z)] ,a = 1, 2. Таким образом, U(z) можем считать новой неизвестной диагональной матрицей-функцией: U(z) = diag {U1(z), U2(z)}. Методика решения задач такого рода описана в [7], U(z) строится в явном виде и представляет собой функцию интегралов типа Коши на действительной положительной полуоси, в структуру которой входит множитель (z — ^1), причем величина µl определяется как решение задачи обращения эллиптических интегралов

1 /“ b(x dx = /

2п J_o r(x)        J_o r(x)

где b(x) = 0 2 (x) — 0 1 (x). Таким образом, разрешимость задачи обращения является одним из необходимых условий применимости метода. В частном случае величина µ _l вычисляется непосредственно. Построим каноническую матрицу решений задачи. Алгоритм, изложенный в [7] , опирается на следующие факты.

Теорема 1. Если Ф(z) - каноническая матрица задачи (7), а дисперсионная матрица-функция Л(z) четна, то справедливо представление:

Л(z) = Ф(z)P(z)Ф ^T (—z).

Доказательство. Для доказательства теоремы исследуем на аналитичность и поведение на бесконечности вспомогательную матрицу-функцию:

Ф(z)=Л(z)[Ф ^T (—z)] ^-1 ,

Рассмотрим поведение Ф(—z) на границах разреза: с учетом четности матрицы-функции Л(z) очевидно равенство между собой ее граничных значений на положительной действительной полуоси

Ф ^- (—^) =Л ⁺ (^)[Ф ⁺ (^)] ^{- т} , Ф ⁺ (—^)=Л ^- ( _М )[Ф ^- ( _М )] ^{- Т} ,ц> 0.

С учетом аналитичности функции Ф(z) во всей комплексной плоскости за исключением действительной оси (по построению) и конечности ее порядка в окрестности бесконечно удаленной точки можем утверждать, что:

Ф(z) = ф(z)P (z)

где P(z) — некоторая полиномиальная матрица-функция. Теорема доказана .

Для окончательной факторизации матрицы канонических решений принципиальным оказывается факт равенства между собой частных индексов задачи Римана. Можно показать, что в частном случае эти значения равны 1.

Лемма 3 . Индекс задачи (7) не зависит от величины действительного положительного параметра l и равен двум: k(G) = 2.

Доказательство. Мы доказали, что detG(^) = detW + (ц) [detW-(ц)] 1.

Следовательно, можем утверждать, что k(g) = 2П [arg detW +И(о,+н - 2П [arg detW — И (o,+h .

При этом значение функций W ± (ц) можно определить в явном виде. Поскольку разрыв на положительной действительной полуоси испытывает только функция Черчиньяни A c (z), то будет выполняться цепочка равенств: W ± (ц) = W(ц) ₊ \ C (^)I = W(ц) ± i ^ц e^-21,ц> 0. Вычисляя требуемый определитель, получаем:

detW±(ц) = detW(ц) + А^(д) • trW(ц) + [А±(д)]2 , или, иначе говоря, detW±(ц) = \detW(ц) — n^e trW (ц).

² ^ ²] ± ^Пц e ^-

<

В точке ц = 0 мнимая часть определителя обращается в нуль, а его действительная часть положительна: Re detW ± (0) = 1 + (2l) ^-1 . В то же время во всех остальных нулях мнимой части действительная составляющая оказывается отрицательной. В силу положительности выражения n^e e ^— • trW(ц) в некоторой проколотой окрестности точки ц = 0 можем утверждать, что в нуле Re detW ± (ц) мнимая составляющая функции detW + (ц) будет строго положительной, в то время как Im detW ^- (ц) строго меньше в силу симметричности их графиков. Следовательно, график функции detW ^± ( ц ) в комплексной плоскости не совершает ни одного полного оборота вокруг начала координат.

Оценим поведение функций W ± (g) на бесконечности:

arg detW + (м) ^ —п, , arg detW - (м) ^ —п, м ^ от.

В силу четности функций detW ± (м) окончательно получим:

[arg detW+(д)](0,+ю) - [arg detW-(м)](0,+^) = 4п, что и доказывает наше утверждение. Лемма доказана.

Следствие. Задача (7) имеет не менее двух линейно независимых решений вне зависимости от величины параметра l.

Доказательство следствия очевидно следует из теоремы Н. П. Векуа [11] .

Лемма 4 . Частные индексы задачи факторизации (7) равны единице.

Доказательство . Покажем, что K i = К 2 = 1. Во-первых, заметим, что K i + K 2 = к, причем в силу леммы 3 K i + K 2 = 2. Поведение функций при |z | → ∞ позволяет утверждать, что

P (z) ^ z ³

a 11 z ^{- κ 1}

a 21 z ^{- κ 1}

a 12 z ^{- κ 2}

a 22 z ^{- κ 2}

откуда очевидно, что K i , K 2 > —2 по определению канонической матрицы [1] . По построению U 2 (z) имеет нуль второго порядка в точке z = 0, а U i (z) в точке £ = M l . Исследуя поведение функций U i , 2 (z) в указанных точках, получаем [8] K i , 2 < 1, что автоматически дает K i = K 2 = 1. Лемма доказана .

Лемма 5 . При любых значениях параметра l >  0 дисперсионная функция A(z) не имеет конечных корней в комплексной плоскости.

Доказательство . Непосредственно вычисляя, что

A(z) = 2y2^i(zM(z), где Qa(z) = Ac(z) + 4^ [| — z2 + (—1)a+ir(z)] , a = 1, 2, r(z) = (z2 — 3/2)2 + 4l, получим представление на линии разрыва:

^ ± ( m ) = ^ _a (^) ± i V n^e ^-^ ² , м € R .

Мнимые части Q ± (g) обращаются в нуль лишь в точке м = 0, причем A(z) = 0, то есть число нулей дисперсионной функции в комплексной плоскости с разрезом по действительной оси вычисляется как

N+2 Nc=2п [argA(z)]c, где С – замкнутый контур вокруг разреза по действительной оси, ориентированный по часовой стрелке, под NC подразумевается количество корней дисперсионного уравнения, принадлежащих контуру, а под N – лежащих внутри контура. Поскольку N = 4, то:

N = V1 + V2 - 2, где va = [0а\с /(2п),0а = argQ+ (рассматриваются главные значения аргумента). Так как Qa(z) = Qa(-z) и Q+(^) = Q-(^) при ^ € R, то va = П [0а(^)]0 +^). Исследуя поведение функций ^а(^), получаем, что vi =0 и V2 = 2, а следовательно и дисперсионное уравнение не имеет конечных корней в комплексной плоскости. Лемма доказана.

Для частного случая справедливо следующее представление:

Теорема 2 . Для любого l > 0 существует каноническая матрица задачи (7) Ф o (z), для которой выполняется тождество:

Л(z)=Ф o (z) Ф Т ( - z)

Доказательство . Из теоремы 1 знаем, что Л(z) = Ф(z)P(z)Ф ^T (—z), при этом Ф(z) — произвольная каноническая матрица задачи (7), а P(z) - матричный полином, определяемый частными индексами задачи. Для любой матрицы канонических решений будет выполняться:

Ф(z) = Ф(г).

Применяя произвольно выбранную каноническую матрицу Ф(z) для факторизации дисперсионной матрицы Л(z) аналогично теореме 1, и учитывая свойства дисперсионной матрицы-функции, для соответствующей полиномиальной матрицы P(z) получим:

P (z)= P T (z), P (z) = P (z).

По определению канонической матрицы Ф(z) ^ Kdiag { z^ ^K 1 , z ^к- }, detK = 0, при |z| ^ от, т.е. с учетом (5) получаем соотношение:

^{P ( z )} ^ ^- z 2

Положим

z ^{κ 1}

5+2 l

⁰    1^-1   2+4 1

_{κ 2} K      ₁

z           ^√ 2+4 l

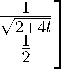
K

- T

Ф o (z) = ф(z)K ^-1

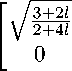
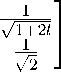
' (-z) ^{K 1}

(-z) ^{K 2}

Матрица-функция Ф o (z) является каноническим решением задачи (7), но в силу леммы 4 K i = К 2 = 1, следовательно, факторизация теоремы

1 для матрицы Ф o (z) переписывается в виде Л (z) = Ф о (z) ^ T (—z). Теорема доказана .

Замечание . Из доказательства теоремы 2 очевидно, что вторым необходимым условием для выполнимости алгоритма поиска канонической матрица решений задачи (7) является равенство частных индексов задачи друг другу.

3 Теорема о полноте

Теорема 3. Для любой вектор-функции Y(^), удовлетворяющей условию Гельдера на замкнутой полуоси [0, +от], имеет место следующее разложение по собственным функциям характеристического урав- нения

Y ( v ) = Y 1

∞

+

F ⁽ п,^) a (п) dn,

где Y i (^) = (A o + A i ^ + A ? v )

+ (A 2 - A ? ^)

^ 2 ^{- 1 / 2} 1

– линейная

комбинация собственных функций дискретного спектра.

Иначе говоря, система собственных функций уравнения (2) { F(п, v ) , П € (0, +го); F _a (^),F e (0, ^), а, в = 1, 2} является полной в пространстве функций, гельдеровых на отрезке [0, +го].

Замечание. Интеграл 0^ F (п, v) a (п) dn понимается как функци- онал, в котором первое слагаемое интерпретируется как главное значение в смысле Коши, второе — согласно определению дельта-функции

Дирака, а(п) имеет своим носителем множество [0, +го].

Доказательство. В силу леммы 1 для доказательства теоремы достаточно доказать разрешимость соответствующей краевой задачи Римана. Предыдущий раздел был посвящен исследованию алгоритма построения аналитической матрицы-функции Ф 0 ( z ) такой, что

[Л +И— 1 Ф о ⁺Ы = [Л —И— 1 ФоЫ.

Воспользовавшись полученными результатами, в силу симметричности дисперсионной матрицы Л(z) после очевидной подстановки получаем:

K+HT [N ⁺ы + Q—W iM ] - [Ф о И^Т [N -Ы + Q ^-W1H =

= ² i—ⁿVe ^ 2 [$ o (^)] T [ ^Л М] 1 Q i ⁽ V ^{) Y (} V), Ц> 0.

Можно доказать, что в условиях теоремы правая часть тождества будет удовлетворять условию Гельдера на промежутке [0, +го]. В силу этого можно воспользоваться интегралом типа Коши:

A(z) = Г     [Ф о HT [Л-(Д)] ^-1 Q i ( v ) Y ( v )~