О методе функциональной коррекции

В большинстве случаев нарушение функционирования того или иного объекта при одних входных данных не исключает правильного функционирования при других данных. В этом обстоятельстве проявляются некоторые резервные возможности, представляющие собой своеобразный внутренний функциональный резерв, который можно назвать также динамическим резервом, т. к. он возникает и изменяется в процессе непосредственного функционирования объекта. Использование функционального резерва для коррекции функционирования будет называться функциональной коррекцией .

Функциональная коррекция заключается в повторном воспроизведении функции объекта в случае нарушения ее выполнения с целью получения адекватного результата за счет преднамеренного преобразования входных, а при необходимости и выходных данных. Под функцией, выполняемой объектом, в данном случае понимаются операция, фрагмент вычислений, реализуемых аппаратурно или программно, и т. п. процедурное действие или взаимоувязанные действия, на выполнение которых отводится ограниченное время.

Для элемента системы, охватываемого функциональной коррекцией, предусматривается возможность представления одних и тех же входных и соответствующих им выходных данных по крайней мере в двух формах — в основной и в резервной, при этом в случае нарушения функционирования элемента обеспечивается переключение с одной формы данных на другую.

Идея функциональной коррекции применительно к частным случаям была развита автором при разработке изобретательских решений [1–4]. Функциональная коррекция табличных сумматоров вычетов [1, 2, 4], построенных на базе элементов сов- падения, основана на аддитивном преобразовании слагаемых и результата. Так, если в основной реализации получается сумма по модулю m вида

Iа + в m= Y , где γ представляет собой наименьший неотрицательный остаток от деления α + β на m, то в случае нарушения функционирования сумматора при повторной реализации на этом же сумматоре получается искомый результат, но с возбуждением иных элементов за счет простого переключения входных и выходных шин, чему соответствует

\ (I а + ^Л а . ⁺1 в ⁺А в|. ) m - Л а - Д 9

= γ . m

В многоярусных структурах, построенных из табличных сумматоров, промежуточные преобразования операндов могут быть исключены. Метод коррекции одиночных ошибок запоминающего устройства [3], который в некоторых публикациях [5, 6] упоминался как метод Долгова, основан на преобразовании данных, представленных в двоичной системе счисления, с помощью инвертирования. Допустим, что в накопителе записано слово 11101011, в котором 8-й двоичный разряд (левый в записи приведенного слова) контрольный. При чтении получено слово 11100011. Проверка на четность показывает наличие нарушения функционирования запоминающего устройства (в данном случае — закрепление нуля в 4-м разряде). Инвертируем считанное слово в порядке входного преобразования (получается 00011100) и запишем в ту же ячейку накопителя. При повторном чтении из этой ячейки (с учетом закрепления нуля в 4-м разряде) будет получено слово 00010100. Последующее инвертирование в порядке выходного преобразования дает записанное в накопителе слово без ошибки. Как и показано в [5], "слово надо инвертировать по методу Долгова" и тогда,

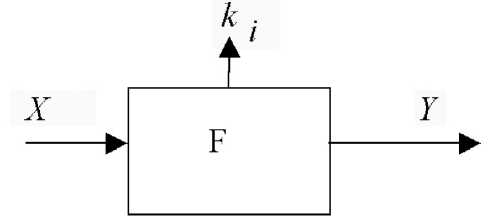
Рис. 1. Элемент, реализующий функцию обработки (F)

например, "код Хэмминга, предназначенный для исправления одной и обнаружения двух ошибок, может совместно с временнóй избыточностью исправлять две ошибки, а не одну".

К сожалению, идея функциональной коррекции отражена лишь в некоторых конкретных технических решениях и до сих пор не стала предметом научного обобщения. В данной публикации хотелось бы восполнить то, что следовало бы сделать гораздо раньше, учитывая что принципы функциональной коррекции хорошо вписываются в современные и перспективные технические и технологические решения.

СУЩНОСТЬ МЕТОДА

Далее функциональная коррекция будет рассматриваться применительно к электронным системам обработки данных, элементы которых охвачены собственным аппаратурным контролем. Подобные системы и их элементы представляют особый интерес в связи с тем, что для их функциональной коррекции обычно требуется относительно небольшая дополнительная аппаратурная избыточность, ограничивающаяся введением только управляющих элементов.

Из вышеизложенного можно прийти к выводу, что функциональная коррекция основывается в основном не на аппаратурной избыточности, а главным образом на временнóй избыточности, при этом следует отметить особо, ранее изученные модели комбинирования аппаратурной и вре-меннóй избыточностей [7] не охватывают функциональной коррекции.

Рассмотрим наиболее общую постановку задачи функциональной коррекции, приводящую к различным вариантам решений. Начнем с исходных данных.

На рис. 1 изображен в условных обозначениях элемент системы обработки данных, предназначенный для реализации функции Y = F ( X ) , где X — переменные входные данные элемента, Y — выходные данные, при этом допустимо представление данных в виде нескольких слов. В дальнейшем F для отличий от других далее рассматриваемых функций будет называться функцией обработки. При выполнении i -й операции формируется двоичный признак контроля k_i . Будем считать, что k i = 0 свидетельствует о правильном функционировании элемента (когда, действительно, Y = F( X )), а значение k i = 1 — о нарушении функционирования (если оказывается, что Y * F( X )).

На рис. 2 приведена схема элемента, реализующего функцию F с функциональной коррекцией. Такой элемент, который далее называется охваченным функциональной коррекцией , строится на основе базового элемента, выполняющего соответствующую функцию.

k i

X

p x

X 1

---►

X 2

p = 0

---► p = 1

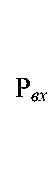
( 1 - k ₁ ) X ₁ + k ₁ ( 1 - k 2 )

( 1 — k , ) X 2 + k i ( 1 — k 2 )

F

( 1 — k ₁ ) i ; + k ₁ ( 1 — k ₂ ) Y ₂

( 1 — k ₁ ) Y ₂ + k ₁ ( 1 — k ₂ ) Y

Y

( 1 ^— P x )( ! ^— k 1 ) ⁺ P x k 2

P x ( ^{1 — k} 1 )⁺( ^{1 —} P x ) ^k 2

p y

Рис. 2. Реализация функции F с функциональной коррекцией

Предусмотрено (см. рис. 2) представление входных данных X в одной из двух форм — основной X ₁ и резервной X ₂ и соответствующее представление выходных данных Y также в двух формах — основной Y 1 и резервной Y 2 (случаи коррекции, предусматривающие представление данных более чем в двух формах заслуживают отдельного рассмотрения).

Для различения того, в какой именно форме представлены данные, в каждом из представлений используются двоичные признаки

и

p x =

p y =

0,

1,

0,

1, если если если если

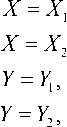
равные нулю для основных представлений X ₁, Y ₁ и единице для резервных представлений X 2 , Y 2 . Цепи хранения и обработки признаков представлений являются избыточными, вводимыми в интересах функциональной коррекции.

Избыточным также является указанный на рис. 2 узел приема входных данных, реализующий функцию Р вх , определяющую зависимость формы выдаваемых узлом данных от значения признака контроля, вырабатываемого базовым элементом. При k i = 0 поступившие входные данные выдаются узлом приема на вход базового элемента в той форме, в которой они поступили, т. е. в этом случае P„_v ( X, ) = X и P„ (X_? ) = X, . В отличие от это- вх 1    1 вх 22

го при k i = 1 реализуется применительно к конкретным поступившим входным данным функция взаимного преобразования форм представления, т. е. P_ra ( X ) = X и P_ei ( X ) = X . вх                         вх

В начале очередного выполнения элементом с функциональной коррекцией функции F в любых случаях осуществляется основная реализация, при которой входные данные без какого-либо изменения поступают через входной узел на входы базового элемента. По результатам основной реализации функции обработки в базовом элементе вырабатывается признак контроля, значение которого k i = 0 при правильном функционировании, а при нарушении функционирования k_i = 1 .

В случае k_i = 0 на выходе элемента, реализующего функцию обработки, получаются выходные данные в той же форме, в какой были представлены входные данные, т. е. на этом очередное выполнение функции F элементом, охваченным функциональной коррекцией, завершается (в данном случае коррекции не потребовалось).

Если же ki = 1, то осуществляется повторная реализация функции F, и в этом случае входной узел Pвх преобразует входные данные в другую форму представления. При этом выходные данные также получаются во второй форме, и вырабатывается признак контроля k2 . При k2 = 0 выполнение функции F элементом, охваченным функциональной коррекцией, завершается (в данном случае коррекция потребовалось), а при k2 = 1 фиксируется случай неосуществимости коррекции.

При сформулированных исходных данных (характеризующих, что дано) требуется для вполне определенной функции обработки F найти функцию входного преобразования P _вх и функцию выходного преобразования P _вых такие, что P _{e m} ( F ( P„ ( X i ) ) ) = X i и P _ ( F ( P ( X ₂ ) ) ) = X 2 .

Выполнение сформулированного требования обеспечивает (при необходимости) возможность взаимного преобразования форм представления полученного результата как для X , так и для Y . В качестве основной формы представления естественно выбрать ту, которая была бы единственной, если бы функциональная коррекция не применялась.

РЕАЛИЗАЦИЯ МЕТОДА

Поставленная задача во многих случаях имеет решения, при этом процесс функциональной коррекции может быть описан следующим образом:

Y Ч

Y = ^{F( X} 1 ) ^и P y = 1, ^{если (1 -} P x ^{)(1 - k} i ^{) + +} P x^k1 ^{(1 - k} 2 ) = 1,

Y 2 = F( ^X 2 ) и P y = 0, если P x (1 ^- k i ) +

+ (1 - P x ) k 1 (1 - k 2 ) = 1.

Класс устройств обработки данных, в которых может успешно применяться функциональная коррекция, является довольно широким.

Особо следует отметить область компьютерных систем и устройств обработки данных параллельного действия, функционирующих в двоичной системе счисления, для которых наиболее простыми и эффективными (с точки зрения коррекции наиболее частых нарушений функционирования типа закрепления нуля или единицы в одном двоичном разряде) функциями P _вх и P _вых является функции инвертирования.

В микроэлектронной технике обычно до 80 %, а иногда и более, занимают шинные связи с двоичным кодированием передаваемой информации, для которых инвертирование является наиболее естественным способом коррекции, особенно при применении программируемых логических инте- гральных микросхем, когда остаются неиспользованные возможности, применимые в интересах контроля и коррекции.

Учитывая, что в компьютерной технике фундаментальным узлом является сумматор, т. к. на его основе строятся практически все другие узлы (вычитания, умножения, деления и т. д.), покажем, что на основе инвертирования осуществимо функциональное резервирование n -разрядного двоичного сумматора, реализующего функцию

IX + Z + O| 2 „=У, где X, Z и Y — двоичные слова слагаемых и суммы; O — значение переноса в младший разряд сумматора.

Обозначим через X и , Z_u и Y _u инверсные значения соответствующих операндов (в резервной форме представления). Значение X и получается из X (основной формы представления) путем инвертирования в X значений всех двоичных разрядов; значения Z _u и Y_u получаются из Z и Y аналогичным образом. В традиционном аналитическом выражении

X = Р (X) = |2"-X-11

и вх                                   I2 n

и

X = Р вх ( X и ) = |2 n - X и - 1 ₂ n

Z u = Р вх ( Z ) = |2 n - X - 1|₂ .

и

Z = Рвх (Zu ) = |2n - Xи -12

Y u = Р вых ( Y ) = |2 n - Y - 1|₂ n

и у = р (У ) = |у -11 вых \ и / I и      I2n .

Рассмотрим значение суммы слагаемых и переноса в младший разряд сумматора, представленных за счет входного преобразования в инверсном виде:

|X и + Z u + 1|2 n = |Р вх ( X ) + Р вх ( Z ) + 1|2 . =

=К2 n - X - 1)+(2 n -Z - 1)+12 n =

= |2 n-(X + Z )-12 n = Y,.

Инвертируя полученный результат Yu в порядке выходного преобразования, переходим от резервной формы представления к основной, что и следовало показать:

Рвых (Y. ) = 2n - Y, -1|2. =

= |² n - ( ² n - ( ^X + ^Z ) - 1 ) - 1[ n =| X + Z + O 2 n = Y .

Сложность технической реализации функциональной коррекции существенно зависит от конкретных условий. Обычно наиболее проста программная реализация, когда можно обойтись без обработки признака формы представления данных, которая находится под программным контролем. Чисто аппаратурная реализация наиболее затруднительна при отсутствии аппаратурного контроля (его приходится дополнительно вводить), при малой разрядности обрабатываемых данных (доля вводимого избыточного оборудования становится существенной), при простоте других вариантов организации коррекции (например, с использованием мажоритарной логики, корректирующих кодов и др.), а также при отсутствии возможностей совместной функциональной коррекции сопрягаемых элементов. При аппаратурной реализации наряду с теми разрядами, для повышения надежности функционирования которых вводится функциональная коррекция, контролем (например, на четность) также должен охватываться признак формы представления данных, при этом явно целесообразны меры исключения влияния отказов избыточного оборудования, вводимого для реализации контроля и коррекции.

Реализация функциональной коррекции, как правило, охватывающей весьма существенный круг наиболее характерных неисправностей функционирования конструируемых и изготавливаемых элементов, обычно не оказывается обременительной, в связи с чем могут быть поставлены вопросы о ведомственной, государственной, а может быть, и международной стандартизации структурных и интерфейсных требований к компьютерным комплектующим в части их охвата функциональной коррекцией. Любой стандартизированный элемент должен быть способен наряду с обычным функционированием работать с данными, представленными в резервной (например, инвертированной) форме и предусматривать сопряжение с другими элементами, реализующее поддержку функционального резервирования. Положительный эффект стандартизации, в первую очередь, ощутили бы те, кто использует недублированные системы и элементы обработки данных на подвижных объектах и кто применяет системы, работающие в жестком цикле с предусмотренным резервом времени, а также многочисленные пользователи компьютерных средств, не имеющие под руками сменных комплектующих.

ЗАКЛЮЧЕНИЕ

Идея функциональной коррекции не ограничивается кругом электронных систем обработки данных. Эта идея, основанная на получении адекватных результатов при обработке данных в разных формах их представления, может быть реализована в объектах и их элементах самой различной природы (технических, механических, электронных, организационных, экономических, информационных и т. д.), и ее воплощение обнаруживается в биологических системах (например, если ребенок при рождении видит мир "вверх ногами", то в дальнейшем включается механизм биологической коррекции и т. д.).