О методе расчета дифракционных интегралов

В работах [1-3] был предложен метод нахождения дифракционного поля за отверстиями с произвольной формой края при условии нахождении точки наблюдения в зоне Френеля. Основой данного метода является преобразование исходного поверхностного дифракционного интеграла в линейный интеграл по контуру отверстия. Это позволяет заметно уменьшить вычислительную сложность подобных дифракционных задач.

В данной работе рассматривается обоснование работ [1-3] на примере сравнения классического решения задачи дифракции на круговом отверстии с решением, полученным методом граничной дифракционной волны.

Для кругового отверстия в случае радиальной симметрии поля в апертуре существует классическое решение в виде одномерного интеграла [4, 5], которое при нормальном падении плоской волны на отверстие радиуса R с центром на оси z имеет вид

W = k exp d

—

r2Yl R ik d + — I • jV0(krr0 d)exp(— ikr2/2d)• rdr

I    2 d J J 0 X '

,

где W - множитель прохождения поля, k = 2 п/ Л - волновое число, к -длина волны, d – растояние по оси z от отверстия до точки наблюдения, 57

J 0 ( x ) – функция Бесселя нулевого порядка. Интеграл (2) можно выразить через функции Ломмеля [4].

Используя результаты работ [1-3], аналогичное выражение для множителя прохождения после параметрического задания окружности и устремления источника в бесконечность (плоская волна) можно записать в виде

w . 1 2П R ( roCOS( t - Ф) - R)

(ik exp     R2 - 2Rr0 cos(t - ф)

< 2 d^x         0         0

+ r o2 ) j dt . (3)

W = £ +

2 п 0 R ² - 2 Rr₀ cos( t - ф ₀) + r 0

Здесь ε = 1, если точка наблюдения находится в освещенной области, и ε = 0 в случае нахождения ее в тени, r 0 , φ 0 – полярные координаты точки наблюдения.

Преобразование интеграла (3) в (2) осуществить не удается. Для их сравнения были проведены вычисления непосредственно по данным формулам с помощью адаптивных квадратурных формул Гаусса– Кронрода, которые показали, что в вычислительном плане в случае нормального падения волны между обоими подходами нет различия (относительная ошибка меньше 10^-12). На основании этого можно предположить, что получено новое интегральное равенство, т.е. равенство выражений (2) и (3). На рис. 1 показаны результаты расчетов по формулам (2) и (3) для распределения уровня поля поперек оси z , которые совпадают между собой.

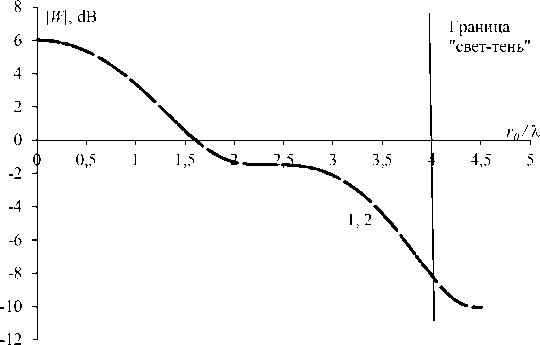
Рис. 1. Распределение уровня поля за круговым отверстием. Плоская волна R= 4 X , 1 - расчет по формуле (2); 2 - расчет по формуле (3)

Таким образом, в работе получено новое решение классической задачи дифракции на круговом отверстии. Совпадение решений в пределах вычислительной погрешности позволяет утверждать, что получено новое интегральное равенство. Решение (3) является более общим, чем (2), поскольку позволяет рассчитать дифракцию волны, не имеющей 58

радиальной симметрии и падающей на апертуру под произвольным углом. Представление дифракционного поля в виде граничной волны выглядит предпочтительным в связи с развитием вычислительной техники и современных программных средств, допускающих эффективное вычисление одномерных дифракционных интегралов.