О некоторых бифуркациях симметричных кусочно-гладких динамических систем на плоскости

Описанию типичных бифуркаций кусочно-гладких динамических систем (векторных полей) на плоскости посвящено большое число работ (книги [1–3] и статьи [4–8]). Естественно изучать бифуркации таких систем, которые обладают различного рода симметрией. Для систем с центральной симметрией в [9] описаны бифуркации сшитых фокусов, а в [10; 11] — бифуркации контуров из двух симметричных периодических траекторий, проходящих через особую точку типа сшитое седло.

В этой работе рассматриваются системы, инвариантные относительно инволюции фазовой плоскости с одной неподвижной точкой. Централь- ная симметрия — частный случай такой инволюции. Описаны бифуркации в окрестности периодической траектории, проходящей через два сшитых седла при типичном двухпараметрическом возмущении системы.

1 Предварительные сведения

Пусть I : R ² ^ R ² — С ” -диффеоморфизм, являющийся инволюцией, то есть 1 ² : = I ° I - тождественное отображение, и O — его единственная неподвижная точка. Основной пример такой инволюции — центральная симметрия x a - x .

Пусть D — разбиение плоскости R ² на замкнутые множества M i , i е {1,..., n}, с С ^да -гладкой границей д M i такие, что M j n M k = = д M j nd M k если j , k e {1,.., n }, j ^ k . Ясно, что M_jk : = M j n M k *0 состоит из связных компонент д M j и д M_k .

Обозначим X r ( M i ) множество векторных полей класса С^г ( r >  1) на M i . Кусочно-гладким векторным полем на R ², задаваемом векторными полями v i eX ^r ( M i ), i e {1,..., n }, назовем класс всех таких векторных полей v : R ² ^ R ², что v ( x ) = v ⁱ ( x ), если x e int M i , i e {1,..., n }. Будем его рассматривать как точку        v = ( v ’,..., v ⁿ )       множества

X ^r ( R ², D ) : = X ^r ( M , ) x ... xX ^r ( M_n ).

Предположим теперь, что разбиение D инвариантно относительно инволюции I, то есть существует биекция а множества индексов {1,...,n} такая, что      Vi e{1,...,n} I(Mt) = Ma(i).         Векторное поле v = (v',...,vn) eXr(R2,D) назовем симметричным или инвариантным относительно инволюции I, если Vi e{1,...,n} dI ° vi = va(i) ° I. Обозначим ΧrI(R2, D) подмножество в Xr (R2, D), состоящее из таких векторных полей. Простейший пример множества Xr (R2, D) получается, если D — разбиение R2 на две полуплоскости R x[0, да) и R x (-да,0], а I — центральная симметрия.

Следуя определению из [1, с. 95] траекториями поля v eX ^r ( R ², D ), будем называть траектории дифференциального включения x e v * ( x ), где v *( x ) = { v i ( x )}, если x e int M i и v *( x ) = { s v ( x ) + (1 - s ) v ^j ( x ), s e [0,1]}, если x e M_h . ij

Точки x e Mj , в которых векторы vi (x) и vj (x) не касаются Mij и направлены в одну сторону от Mij, будем называть простыми. Пусть a e Mij — простая точка и для определенности vi (a) и vj (a) направлены внутрь Mi. Тогда положительная (отрицательная) полутраектория поля vi ( vj ), начинающаяся в точке a , является положительной (отрицательной) полутраектория поля v, начинающейся в этой точке, или ее частью. Для остальных точек a g Mj в v* (a) существует единственный вектор vM (a), касающийся Mi..

i j

Локальные C” -координаты (x1, x2) в окрестности V(a) точки a g Mi. назовем правильными, если точка a имеет нулевые координаты, а Mi о V(a) (Mj о V(a)) задается неравенством x2 20(x2 ^0 ). В этих координатах va (x) = Paa (x1, x2)d / dx1 + Pa (x1, x2)d / dx2, где pa, Pa g Cr, aG {i, j}.

Пусть векторы v i ( a ) и v ^j ( a ) ненулевые и только один из них для определенности v i ( a ) касается M ij : P ₂ i (0,0) = 0, P j (0,0) ^ 0. Если P i (0,0) d P ₂ i (0,0)/ d x 1 >  0, а P 1 j (0,0) >  0 ( P 1 j (0,0) <  0), то точку a будем называть сходящейся (расходящейся) развилкой (рис. 1а).

Пусть векторы v i ( a ) и v ^j ( a ) направлены в разные стороны от M ij , то есть P i (0,0) P ₂ j (0,0) <  0. Тогда для точек x g M ij , достаточно близких к a , определен вектор v _M ( x ) = P i ( x 1 ) d / d x 1 + 0 -d / d x ₂, касающийся M j , i j                                                                                                                          j

PiPj-PjPi при этом [1, c. 163] PJ(xx) = 1 2---1 — (x,0). Точку a будем называть

• ¹        P ₂ j - P 1 ^{J      1}

квазиседлом (рис. 1б), если P i (0) = 0 , ( P i ) ‘ (0) P ₂ i (0,0) <  0 .

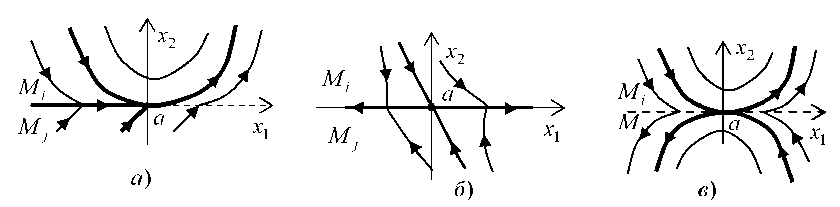
Рис. 1. Особые точки: а) сходящаяся развилка; б) квазиседло; в) сшитое седло

Пусть векторы v i ( a ) и v ^j ( a ) ненулевые и оба касаются M ij , то есть P [ (0,0) = P ₂ ^J (0,0) = 0. Пусть P a (0,0) d P₂ ^a (0,0)/ d x 1 >  0 для a g { i , J } . Точку a назовем сшитым седлом , если P[ (0,0) P^J (0,0) <  0 (рис. 1в). Положительные (отрицательные) полутраектории поля v , начинающиеся в точке a как положительные (отрицательные) полутраектории векторных полей v i и v ^j , будем называть выходящими ( входящими ) сепаратрисами точки a .

2    Условия

Пусть { v _£ } _{£ еE} o — семейство полей v _£ = ( v 1 ,..., v " ) еХ Г ( R ², D ), зави- о сящих от параметра £ , меняющегося в некоторой окрестности E двумерного евклидова пространства. Будем предполагать, что отображения M i xE ⁰ э ( x , £ ) a v £ ( x ) i е {1,..., n}, принадлежат классу C^r ( r >  2).

Пусть для векторного поля v ₀ точки 0 0 ( 0 0 ^ O ) и O 0 = I ( O 0) — два симметричных сшитых седла, а L — дуга траектории с концами в точках 0 0 и 0 ⁰, принадлежащая выходящей сепаратрисе точки 0 0 и входящей сепаратрисе точки 0 0 , причем все точки пересечения L с д M i , i е {1,..., n }, отличные от 0 0 и 0 0 , являются простыми. Обозначим L ₂ : = I ( L ₁). Замкнутая кривая Г : = L 1 u L ₂ является периодической траекторией поля v о . По теореме Жордана R ²\ Г состоит из двух связных компонент K + и K - .

Одна из компонент K + или K - (для определенности пусть K + ) не пересекается с сепаратрисами точек 0 1 ⁰ и 0 ⁰ (рис. 2).

Пусть 0 ⁰ е M ij , ( x ₁, x ₂) — правильные координаты в окрестности V ( 0 1 ⁰) точки 0^о, v a ( x ) = P^ ( x j , x ₂, £ ) д / д x 1 + P ^ ( x 1 , x ₂, £ ) д / д x ₂ для a = i₁ и a = j₁. Мы можем считать, что р i ¹ (0,0,0) >  0, p j ¹ (0,0,0) <  0, а дуга L содержит положительную полутраекторию поля v ₀ ^{i 1} , начинающуюся в точке 0 ₁⁰ .

Пусть ^:( - 1 , l ) ^ V ( 0 J ⁰) отображение, ставящее числу u е ( - 1 , l ) точку с координатами ( u , 0). Пусть точка a₁ е L ₁ n int M i , а T ₂:( - 1,1) ^ int M^ — C^r -гладкое вложение такое, что T ₂(0) = a ₁, T ₂(0,1) c K ₊ , трансверсальное траекториям поля v 0 .

Согласно [4] и [10] при достаточно малом u е (0, l ) определено отображение по траекториям поля v ₀: T 1 ( u ) a T ₂( f ₊ ( u )), и е [0, u ), и отображение по траекториям поля - v ₀: T 1 ( u ) a I ( T ₂( f - ( u ))), u е [0, u ), такие, что f ± ( • ) е C r , f ± (0) = f ‘ (0) = 0, f ± ‘ (0) >  0. Число Л : = f +" (0)/ f "(0) не зависит от произвола в выборе отображений T₁ и Т ₂. Назовем его характеристикой контура Г .

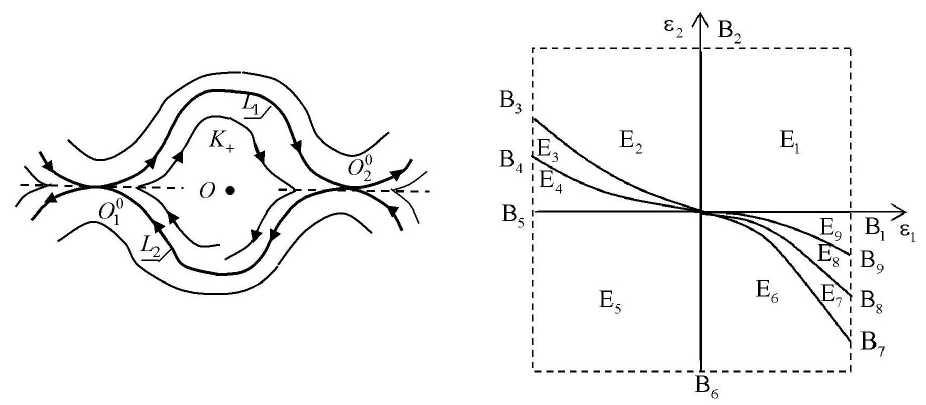
Рис. 2. Контур из сепаратрис сшитого Рис. 3. Бифуркационная диаграмма седла. Характеристика контура Л <  1

По теореме о неявной функции найдется такая окрестности нуля E’ с E , что для каждого a е {i 1 , j 1 } существует единственная C^r -функция E _a : Е‘ ^ R такая, % _а (0) = 0 , d P ^ ( E _a ( е ),0, £ ) / д x 1 = 0. Обозначим O _a ( е ) точку в окрестности точки O 0 с координатами ( E _a ( е ),0), ае {i 1 , j 1 }, E : = E j — E i, . Пусть I ( M^) = M^ , I ( M j ) = Mj . Обозначим O i ( е ) : = I ( O i ( е )) , O j ( e ) : = I ( O j ( e )). Мы можем считать окрестность E‘ выбранной столь малой, что при е еЕ‘ E ( e ) = 0 ( E ( e ) * 0) точки O i ( е ) и O j ( е ) , O i ( е ) и O j ( е ) ) совпадают (не совпадают) и являются сшитыми седлами (сходящимися развилками в случае E ( e ) <  0 и расходящимися развилками в случае E ( e ) >  0). Считая E’ достаточно малой, из [1, с. 180] получаем, что при % ( е ) * 0 на дуге M i ■ ( k = 1,2 ) между точками O i ( е ) и O j ( е ) существует единственная особая точка — квазиседло O ij ( е ) .

Поскольку пересечение дуги £ ₁\{ O ₁ ° , O 0 } с границами множеств M_k состоит только из простых точек, то окрестность E’ можно выбрать так, что положительная (отрицательная) полутраектория поля v _E , е еЕ‘ , начинающаяся в точке O i ( е ) ( O j ( е ) ) как положительная (отрицательная) полутраектория поля v £ ( v £ ² ), пересекает трансверсаль T ₂( - 1,1) в точке T₂( n 1 ( s )) ( Т ₂( п ₂( е ))), где п _к е C^r , п _к (0) = 0, к = 1,2. Обозначим П ^: = П 1 ^- П 2 .

Потребуем, чтобы производные d E (0)/ ds = 0 и д п (0)/ ds = 0 были линейно независимы.

Тогда существуют такие C^r -координаты ( £ 1 , £ ₂) в окрестности E’’ с E’ нуля в пространстве параметров, что для любого £ е E’’ ^ ( £ ) = £ 1 , п ( £ ) = £ ₂ . В дальнейшем будем отождествлять точку £ еЕ’’ со строкой ( £ 1 , £ ₂) е R ² ее координат.

3    Бифуркации периодической траектории, образованной сепаратрисами сшитых седел

Теорема. Пусть для семейства векторных полей { v _£ } _{£ еЕ} 0 характеристика контура Г удовлетворяет условию А <  1 . Тогда существуют окрестность U = I(U ) контура Г и разбиение окрестности нуля Е = ( -5 , 5 )² на плоскости параметров на множества B _o = {(0,0)} , B k , Е k , к е {1,2,...,9} , где (рис. 3)

B i = (0, 5 ) х {0} , В ₂ = {0} х (0, 5 ) , В- {( £ 1 , £ ₂): £ ₂ = в>£} , вм( -5 ,0) ^ (0, 5 ) , в ₁ е С, в^ - ) = в ' (0 - ) = 0 , i = 3,4 , в 4 ( £ 1 ) < в з ( £ 1 ) , В ₅ = ( - 5 ,0) х {0} , В ₆ = {0} х ( - 5 ,0) , B j = {( £ 1 , £ 2 ): £ 2 = e j ( £ 1 )} , в j : (0, 5 ) ^ ( - 5 ,0) , в j е C^r, e j (0 + ) = в ' (0 + ) = 0 , j = 7,8,9 , Е к — компонента Е \ U k = ₀ В _к, содержащая В к и В к _{+ 1} ( В ₁₀ : =В 1 ), такие, что схемы векторных полей v _£ в U ( Г ) при £ еЕ имеют вид, изображенный на рисунке 4.

Случай характеристики контура А >  1 сводится к случаю А <  1 переходом к семейству векторных полей { - v _£ } _{£ еЕ} 0 .

Доказательство . Введем отношение эквивалентности: z 1 ~ z ₂, если I ( z 1 ) = z ₂. Фактор-пространство Ml : = ( R ²\{ O })/ ~ является гладким многообразием, а проекция p : R ² \ {O } ^ Ml — двулистным C ” -накрытием [12]. В силу инвариантности разбиения D , не совпадающие между собой множества p ( M l i ), i е {1,2,..., n } , образуют разбиение D многообразия M l на множества M I j , j е {1,2,..., n} , с гладкими границами, пересекающимися друг с другом только по границам. На многообразии M l с разбиением D ) определены кусочно-гладкие векторные поля V _£ = ( » £ ,..., Vⁿ _E ), где векторное поле v £ на M j задается следующим образом. Если z е M j , то пусть z е M i — точка, для которой z = p ( z ). Так как dp v _E ⁽ i ) ( I ( z )) = dp v £ ( z ), то можно положить V^J_£ ( z ) : = dp v £ ( z ).

Векторное поле V0 имеет сшитое седло O0 = p(O10) = p(O0) и периодическую траекторию Г = p(Г) = p(L1) = p(L2), проходящую через O0 . Бифуркации такой траектории изучены в работе [4]. Из нее следует, что би- фуркационная диаграмма семейства векторных полей % в некоторой окрестности U кривой Г имеет указанный в теореме вид с тем изменением, что во всех формулировках, где речь идет об особых точках, надо заменить °ц(г) и Oi2(г), °А(г) и Oj2(г)), Oiiji(s) и O2j2(s) соответственно на Р ( O^ )) = Р ( Oi2(S)), P ( Oj^ )) = P ( Oj2(S )), p(Oi,j,(£))=p (Oi, jS£)) -

Можно считать, что U = p ^{- 1}(U ) — цилиндрическая окрестность Г , I(U ) = U , отображение T ₂ и E = ( -5 , 8 )² выбраны так, что T ₂( - 1,1) — трансверсаль для траекторий полей v _£ , г gE и не содержит симметричных точек, а U \ T 2 ( - 1,1) односвязное множество.

При г gE ₇ поле v _£ имеет в U устойчивую и неустойчивую периодические траектории, не гомотопные нулю в U . Пусть Г _г — одна из этих траекторий. Тогда р ^-1( Г _г ) либо 1) является периодической траекторией, либо 2) состоит из двух периодических траекторий Г г и г 2 = i ( г г ).

В случае 2) г г и Г 2 негомотопны нулю в U и потому пересекают трансверсаль T ₂( - 1,1) в двух разных точках z 1 и z ₂. Тогда периодическая траектория Г _г должна пересекать трансверсаль р ( T ₂( - 1,1)) также в двух разных точках р ( z 1 ) и р ( z 1 ), что невозможно. Таким образом, возможен только случай 1) . Поэтому в окрестности U кривой Г лежат ровно две периодические траектории поля v _£ . Поскольку дуга траектории поля v _£ с концами на трансверсали T ₂( - 1,1) проецируется в дугу траектории поля v _e с концами на трансверсали р ( T ₂( - 1,1)), то функция последования по траекториям поля v _e на трансверсали р ( T ₂( - 1,1)) является и функцией последования по траекториям поля v ε на трансверсали T ₂( - 1,1). Следовательно, в U одна периодическая траектория устойчивая гиперболическая, а вторая неустойчивая гиперболическая.

Аналогично получаем существование периодических траекторий при £ gE i , i g {1,2,3,8,9}, £ gB j , j g {0,1,2,3,7,8,9} и сепаратрисных контуров при £ gB k .k g {4,8}.

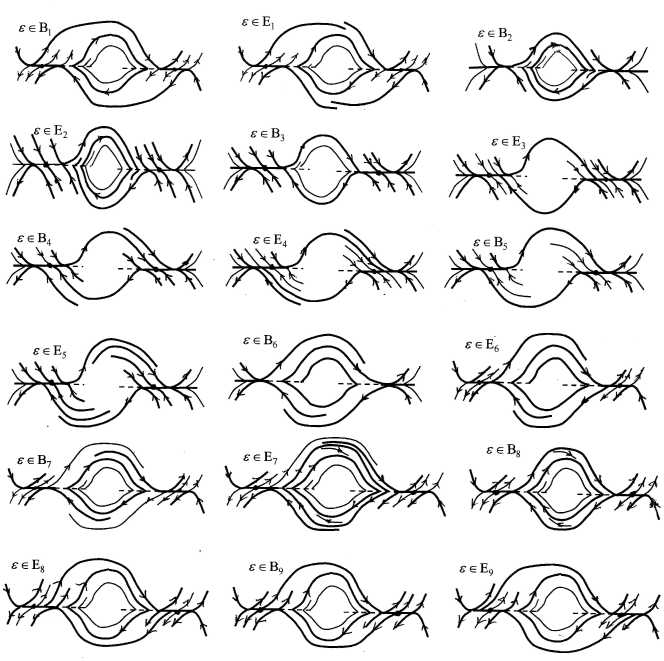
Рис. 4. Перестройки фазовых портретов

Заключение

Хотя изучение бифуркаций кусочно-гладких динамических систем с симметрией представляет несомненный интерес, пока имеется мало результатов в этом направлении. Поэтому продолжение исследования таких бифуркаций является актуальной задачей. В данной работе рассматривалось двухпараметрическое семейство кусочно-гладких систем на плоскости, инвариантных при инволюции, имеющей единственную неподвижную точку. Описаны бифуркации «полуустойчивой» периодической траектории, проходящей через две симметричные особые точки. В частности, найдены области параметров, при которых система имеет устойчивую периодическую траекторию. Этот результат может быть полезен для теории колебаний.