О некоторых «подводных камнях» при использовании простой линейной регрессии и универсальных компьютерных средств

Решение экономических задач, бизнес и многих других процессов без использования компьютерных средств сегодня трудно вообразить, ибо в силу их сложности и большой трудоемкости результаты могут носить приближенный характер, а нередко оказывается невозможными.

Компьютерные средства для решения указанных выше задач отличаются многообразием – это и универсальные пакеты прикладных программ, специализированные пакеты и комплексы программ, отдельные уникальные программы. Их использование, как правило, связано с необходимостью специальной подготовки пользователей, достаточно большими материальными затратами и трудоемкостью, практически всегда имеющими место ограничениями.

В данной работе рассматривается использование стандартных компьютерных средств для решения экономических задач и бизнес-процессов, доступных широкому кругу пользователей, таких, например, как электронный процессор Microsoft Excel и достаточно мощная надстройка к этому процессору – РН Stat.

Объекты и методы исследований

Программный продукт MS Excel или, как это принято называть в экономике – программа калькуляции таблиц и деловой графики [1-3], удовлетворяет самым высоким запросам пользователей, постоянно совершенствуется и, даже, начиная с ранних версий 3.0÷6.0, не говоря о современных – 2000 ÷ 2010, является мощным универсальным средством, позволяю- щим решать разнообразные задачи: от расчета подоходного налога, до составления финансового отчета крупной корпорации. Возможности Excel не ограничиваются только выполнением вычислительных операций, они значительно шире – это и обработка текста, управление базами данных, что во многих случаях превосходит специализированные программы-редакторы или программы управления базами данных.

В MS Excel встроено множество функций. Он предлагает удобные средства создания простых и сложных формул, используя ссылки на ячейки, операторы и функции. Мастер функций позволяет легко строить сложнейшие формулы, которые можно редактировать, копировать и перемещать по рабочему листу и рабочей книге. Привлекательные черты этого стандартного программного продукта:

• •    является неотъемлемой частью рабочего места пользователей, поэтому отпадают затраты на дополнительное программное обеспечение;

• •    простота, как для обучения, так и для использования;

• •    графические и статистические функции, вычислительные и аналитические возможности MS Excel оперируют с теми же рабочими листами, которые пользователи применяют для хранения данных;

• •    часть графических функций процессора создает лучшую, более ясную визуализацию и представление данных, чем другие пакеты программ.

• •    MS Excel совместим со всеми

известными приложениями Microsoft Office.

Сведения по использованию MS Excel весьма подробно описаны в многочисленных источниках; адресованы они как начинающим, так и профессиональным пользователям. В данной статье основное внимание обращено не на основы работы с MS Excel, а на использование в решении задач, связанных с моделированием бизнес-процессов. Что касается надстройки РН Stat, то она оказывается весьма удобной и эффективной, поскольку большинство задач бизнес-процессов, являются стохастическими, связанными с оптимизацией, прогнозированием и, следовательно, с использованием математических моделей, способов, приемов и методов математической статистики.

Результаты и их обсуждение

Исследование моделей, так называемой, коммерческой статистики в решении задач бизнес-процессов, имеет широкое распространение и возможности и представляет значительный интерес. Статистические методы применяют в самых разнообразных сферах бизнеса. В бухгалтерском учете они используются для извлечения и анализа выборок данных, подвергающихся аудиторской проверке, а также для определения затрат при исчислении себестоимости. В финансовом деле статистика позволяет принять правильное решение при выборе объектов капиталовложений и отслеживать финансовые показатели, изменяющиеся во времени. Менеджеры используют статистические методы для улучшения качества производимой продукции или предоставляемых услуг. В маркетинге статистика позволяет оценить долю клиентов, предпочитающих один вид продукции другому, выяснить причины этого явления, а также определить, какая из рекламных стратегий увеличивает сбыт продукции. То есть круг пользователей статистических методов весьма широкий.

Используя программу MS Excel, пользователь должен не только делать правильный выбор метода, но и хорошо знать условия его применения, иметь глубокое понимание математических моделей, статистических понятий, связанных с решаемой задачей, чтобы предотвратить некорректный анализ или другую ошибку. Одновременно для правильного применения MS Excel необходимо знать ограничения, которые налагаются, учитывать возможности, недостатки, памятуя о том, что не существует единого оптимального, абсолютного способа, процедур применения программы Microsoft Excel, который подошел бы абсолютно всем пользователям в решении многообразных задач бизнеса.

Поскольку в бизнес–процессах, решении экономических задач значительное место занимают статистические данные, способы, методы и приемы их обработки, анализа, предсказания значений зависимой переменной, а также, учитывая ограниченный объем данной статьи, то основное внимание обращено на использование модели простой линейной регрессии, условия ее применимости и способы проверки этих условий.

Известно, что для определения тесноты связи между показателями, не находящимися в функциональной зависимости, широко используются методы корреляционного и регрессионного анализа, Корреляция представляет собой вероятностную зависимость между явлениями, не имеющую строго функционального характера. Корреляционная зависимость может быть выявлена как между двумя количественными признаками, так и между многими величинами. В последнем случае приходится иметь дело с множественной корреляцией.

Используя уравнение регрессии, можно получить удовлетворительное значение результативного признака только в том случае, если значения факторных признаков, подставляемых в уравнение регрессии, близки к тем эмпирическим значениям, на основе которых определяются параметры уравнения.

Непременным условием применения корреляционного и регрессионного анализа является обеспечение: репрезентативности статистических данных, обоснованность применения вероятностной схемы к изучаемому явлению. Практически это сводится к выбору уравнения соответствующей кривой – логарифмической, параболы, гиперболы и др.

Теснота связи между изучаемыми явлениями измеряется корреляционным отношением для криволинейной зависимости; для прямолинейной зависимости исчисляется коэффициент корреляции.

Регрессионные модели отличаются большим разнообразием. Зависимость между двумя переменными может быть разной: от самой простой до крайне сложной. Пример простейшей (линейной) зависимости показан на рис.1.

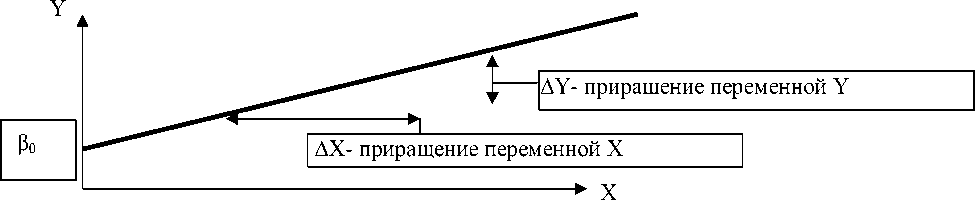
Рисунок 1 - Положительная линейная зависимость.

Простая линейная регрессия выражается как: Yi = во + Pi * Xi + Ei            (1), где: β 0 - сдвиг (длина отрезка, отсекаемого на координатной оси прямой Y), β 1 - наклон прямой Y, ε i - случайная ошибка переменной Y в i - м наблюдении. В этой модели наклон β 1 представляет собой количество единиц измерения переменной Y, приходящихся на одну единицу измерения переменной Х. Эта величина характеризует среднюю величину измерения ---------------»x Рис. 2a Положительная линейная зависимость * • • • • • X Рис. 2в Переменные X и Y не зависят друг от друга Y ------------->Х Рис. 2д U - образная криволинейная зависимость Известно [2], что условиями применения регрессионного анализа являются следующие: 1.    Ошибка должна иметь нормальное распределение; 2.    Вариация данных вокруг линии

переменной Y(положительного или отрицательного) на заданном отрезке оси Х. Сдвиг β 0 - представляет собой среднее значение переменной Y, когда переменная Х равна 0. Последний компонент модели ε i является случайной ошибкой переменной Y в i - м наблюдении. Выбор подходящей математической модели зависит от распределения значений переменных Х и Y на диаграмме разброса. Различные виды зависимости переменных показаны на рис. 2 а-е. Рис. 26 Отрицательная линейная зависимость X Рис. 2г Положительная криволинейная зависимость Y * * *- х Рис. 2е Отрицательная криволинейная зависимость регрессии должна быть постоянной (свойство гомоскедастичности); 3. Ошибки должны быть независимыми. Первое предположение о нормальном распределении ошибок требует, чтобы при

каждом значении переменной Х ошибки линейной регрессии имели нормальное распределение. Второе условие – гомоске-дастичность, заключается в том, что вариация данных вокруг линии регрессии должна быть постоянной при любом значении переменной Х. Это означает, что величина ошибки, как при малых, так и при больших значениях переменной Х должна изменяться в одном и том же интервале. Свойство гомоскедас-тичности очень важно для метода наименьших квадратов, с помощью которого определяются коэффициенты регрессии. Если это условие нарушается, то необходимо применять либо преобразование данных, либо метод наименьших квадратов с весами [2].

Третье предположение, о независимости ошибок, заключается в том, что ошибки регрессии не должны зависеть от значения переменной Х. Это условие особенно важно, если данные собираются на протяжении определенного отрезка времени. В этих ситуациях ошибки, присущие конкретному отрезку времени, часто коррелируют с ошибками, характерными для предыдущего периода.

С учетом этих предположений в качестве оценки генеральной совокупности β 0 и β 1 можно использовать сдвиг b 0 и наклон b 1 прямой Y. Таким образом, уравнение регрессии принимает вид:

Х= b o +b i *X i (2), где: Ý – предсказанное значение переменной Y для i-го наблюдения; Х i - значение переменной Х в i-м наблюдении.

Т.е., простая линейная регрессия выражается, как «предсказанное значение переменной Y, равное сумме сдвига и наклона, умноженное на значение переменной Х».

Для того, чтобы предсказать значение переменной Y, в уравнении (2) необходимо определить два коэффициента регрессии – сдвиг b 0 и наклон b 1 прямой Y. Вычислив эти параметры, проведем прямую на диаграмме разброса. Затем можно визуально оценить, насколько близка регрессионная прямая к точкам наблюдения.

Критерии соответствия можно задать разными способами. Проще всего минимизировать разности между фактическими значениями Y и предсказанными значениями Ý. Однако, поскольку эти разности могут быть как положительными, так и отрицательными, следует минимизировать сумму их квадратов. Из уравнения (2) следует:

п п

^№—Yi)2 = ^(Y - (bo + bi * Xi))2 (3) i=i i=i

Здесь параметры b 0 и b 1 неизвестны. Таким образом, сумма квадратов разностей является функцией, зависящей от сдвига b 0 и наклона b 1 выборки Y. Для того, чтобы найти значения параметров b 0 и b 1 , минимизирующих сумму квадратов разностей, применяется метод наименьших квадратов. Для иллюстрации данного положения построим диаграмму разброса на примере зависимости доходов сети магазинов от их площадей (статистика реальных данных для конкретной организации по годам взята за 12 лет).

Ниже (рис. 3) приводится диаграмма разброса, построенная с помощью MS EXCEL и нанесенной на нее прямой Y, т.е. линией регрессии, и найденным соот-ветственно ее уравнением:

Y = 0.9645 + 1.6699X (4)

Как следует из указанной диаграммы, точность определения уравнения регрессии (аппроксимации) составляет 0.9042 (R 2 = 0.9042), сдвиг b 0 - 0.9645, наклон b 1 - 1.6699.

Применяя регрессионную модель для прогнозирования, необходимо учитывать лишь допустимые значения независимой переменной. В этот диапазон входят все значения переменной Х, начиная с минимальной и заканчивая максимальной. Таким образом, предсказывая значение переменной Y при конкретном значении переменной Х, мы выполняем интерполяцию между значениями переменной Х в диапазоне возможных значений. Однако экстраполяция значений за пределы этого интервала невозможна [2]. Любая попытка экстраполяции означает, что мы предполагаем, будто линейная регрессия сохраняет свой характер за пределами допустимого диапазона.

Для того чтобы предсказать значение зависимой переменной по значениям независимой переменной в рамках избранной статистической модели, необходимо оценить изменчивость. Существует несколько способов оценки изменчивости. Один из них использует общую сумму квадратов (total sum of squares – SST), позволяющую оценить колебания значений Y вокруг среднего значения Y ср . Полная вариация, представляющая собой полную сумму квадратов, делится на объяснимую вариацию, или сумму квадратов регрессии (regression sum of squares – SSR, or explained variation) и необъяснимую вариацию

(unexplained variation), или сумму квадратов ошибок (error sum of squares – SSE). Объяснимая вариация характеризует взаимосвязь между переменными Х и Y, а необъяснимая зависит от других факторов (рис.4).

Диаграмма разброса

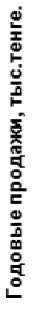
у = 1,669х + 0,964 R2 = 0,904

Площадь, тыс.кв.м.

Рисунок 3 - Диаграмма разброса и линия, построенная с помощью программы MS EXCEL.

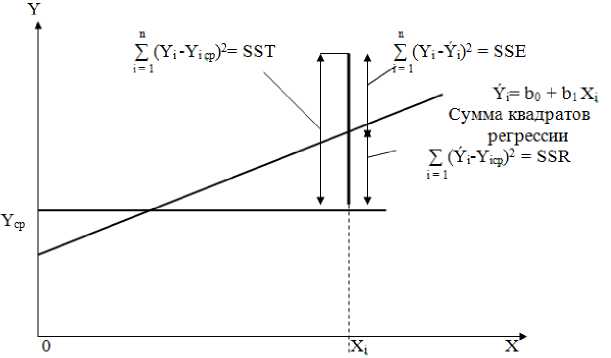
Рисунок 4 - Оценки изменчивости в модели регрессии.

Сумма квадратов регрессии (SSR) представляет собой сумму квадратов разностей между Ý i (предсказанным значением переменной Y) и Y cр (средним значением переменной Y). Сумма квадратов ошибок (SSЕ) - является частью вариации переменной Y, которую невозможно описать с помощью регрессионной модели. Эта величина зависит от разностей между наблюдаемыми и предсказанными значениями.

Таким образом, оценками изменчивости в регрессионной модели являются:

Полная сумма квадратов (SST), равная сумме квадратов регрессии, плюс сумма квадратов ошибок

SST = SSR - SSE (5)

Иначе, полная сумма квадратов (SSТ) может быть представлена как сумма квадратов разностей между наблюдаемыми значениями переменной Y и ее средним значением: п

SST = ^(Y i — Y icp )²       (6)

i=l

Сумма квадратов регрессии (SSR) равна сумме разностей между предсказанными значениями переменной Y и ее средним значением: п

SSR = ^(Y i — Y icp )²         (7)

i=l

Сумма квадратов ошибок (SSЕ) равна сумме квадратов разностей между наблюдаемыми и предсказанными значениями:

n

SSE = ^(Yi — Y,)2 (8), i=l

Суммы квадратов, вычисленные с помощью программы MS Excel по формулам (6 – 8), оказались равными: SSR=105.7476, SSЕ = 11.2967, SST = 116.9543

Нетрудно проверить по формуле (5), что полная сумма квадратов разностей SST и SSR равна 116.9543 (116.9543 = 105.7476 + 11.2967)

Следует обратить внимание на то, что в некоторых версиях программы MS Excel величина SSR представляется в так называемом научном формате. Этот формат применяется для представления очень маленьких или очень больших числовых величин [2,3]. Число, стоящее после буквы Е, задает количество позиций, на которое следует перенести десятичную точку: влево – если это число отрицательное; вправо – если положительное. Например, запись 3,7431 + 02 означает, что десятичную точку следует перенести на две позиции вправо, т.е. число равно 374, 31. Запись 3,7431 – 02 означает, что десятичную точку нужно перенести на две позиции влево, т.е. число равно 0,037431.

Кроме того, следует учесть, что при записи чисел в научном формате количество значащих цифр, как правило, уменьшается, и числа могут округляться.

Заключение.

Выполненные решения многочисленных примеров и реальных задач с использованием MS Excel и РН Stat2 показали, что в диаграммах разброса и графиках остатков данные нередко отличаются друг от друга и иллюстрируют такую ситуацию, в которой эмпирическая модель значительно зависит от отдельного отклика [4]. Чтобы избежать ошибки и «подводные камни» при регрессионном анализе, необходимо:

• •    Помнить, что графики остатков являются необходимым инструментом регрессионного анализа и должны быть его неотъемлемой частью.

• •    Анализ возможной взаимосвязи между переменными Х и Y всегда следует начинать с построения диаграммы разброса;

• •    Прежде чем интерпретировать результаты регрессионного анализа, следует проверять условия его применимости;

• •    Для определения соответствия эмпирической модели результатам наблюдения и обнаружения нарушены ли условия гомо-скедастичности, целесообразно построить и

• исследовать график зависимости остатков от независимой переменной;

• •    Для проверки предположения о нормальном распределении ошибок следует использовать гистограммы, диаграммы «ствол и листья», блочные диаграммы и кривые нормального распределения (кривые Гаусса). При этом полезно оценить все основные моменты распределения кривой Гаусса – математическое ожидание, дисперсию, коэффициенты ассиметрии и эксцесс;

• •    Если условия применимости метода наименьших квадратов выполняются, необходимо проверить гипотезу о статистической значимости коэффициента регрессии и построить доверительные интервалы, содержащие математическое ожидание и предсказанное значение отклика;

• •    Если условия применимости метода наименьших квадратов не выполняются, следует использовать альтернативные методы, например, модели квадратичной или множественной регрессии;

• •    Не следует применять экстраполяцию, то есть необходимо избегать предсказаний значения зависимой переменной за пределами изменения независимой переменной;

• •    Нужно иметь в виду, что корреляция между переменными не означает наличия причинно-следственной зависимости между ними, поскольку статистические зависимости не всегда являются причинно-следственными.