О полном описании весового класса целых функций

Множество задач теории функций комплексного переменного посвящено исследованию специальных классов функций. При их изучении возникает необходимость получения полного описания таких классов.

Описанием корневых множеств и получением факторизационных представлений многочисленных классов функций занимались и продолжают заниматься специалисты комплексного анализа.

Интерес к подобным вопросам возник благодаря работам о нулях целых функций, рост которых при приближении к бесконечно удаленной точке задан, задачам о факторизации функций ограниченного вида и классов Харди в единичном круге.

Исследованием различных классов функций, получением их полного описания активно занимаются современные авторы, такие, как Б. И. Левин, М. М. Джрбашян, Н. В. Говоров, А. А. Гольдберг, И. В. Островский, A. M. Седлецкий, Ф. А. Шамоян, Б. И. Коренблюм, К. Сейп, Б. Н. Хабибуллин и многие другие.

Прежде чем сформулировать основную задачу, введем необходимые обозначения.

Обозначим через C комплексную плоскость. Рассмотрим на ней множество всех целых функций H ( C ) . Пусть 0 <  р < += , 0 <  р < += .

Определим следующий класс функций:

нр (C) = | f с H (C): J(lnMfp dr < +« • -r

В данной работе получено полное описание функций класса H р р ( C ) при целых р и р , не являющихся целыми, а именно построено фактори-зационное представление, а также получено описание корневых множеств класса.

Случай р = 1 описан в [1].

Основной и вспомогательные результаты работы доказываются с применением методов, изложенных в работах [2-6].

Корневые множества других весовых классов целых и субгармонических функций комплексного переменного были описаны автором в работах [4-6].

• 1    Постановка задачи

Теорема А. Пусть р — нецелое неотрицательное число, 0 <  р <+= , р - 1 <  q < р . Тогда эквивалентны следующие утверждения:

• 1)    f с н р ( C ) ;

• 2)    f допускает представление

  +=/           I

  f ( z ) = z m П 1 — - exp £ ¹ z-

  
  

  k = 1 V

  
  

  z

  
  

  ' k 2

  
  

  ^ j I z

  
  

где z с C , h ( z ) — многочлен степени меньше р , m — некоторое неотрицательное целое число, { z_k } += — последовательность комплексных ™ п^р ( 2 ^k ) чисел, удовлетворяющая условию   —- ---<+= .

2 ^{к р р}

Теорема Б. Пусть р с N . Тогда следующие два утверждения эквивалентны:

• 1)    f с н р ( C ) ;

• 2)    f допускает представление

  4^/         I

  f ( z ) = z m П 1 - - exp £ ¹ z-

  
  

  k = 1 V

  
  

  z

  
  

  ' k 7

  
  

  ^ j I z

  
  

где z g C, h ( z ) — многочлен степени меньше, чем р , m g Z , m >  0 ,

{ z . }:,

— произвольная последовательность комплексных чисел, для ко-

™ n p ( 2 ^k ) ^тоР^ых £ ~v p~ <^+A , k =1 ²

Sf (r ) = £ 717

I ^z i I^s r ^zi

k

удовлетворяет условию

т (Sf (r))P dr

< +да .

2 Важные теоремы

Доказательство основных теорем строится с использованием следующих утверждений.

Для f g H ( C ) определим Z f = { z g C : f ( z ) = 0 } .

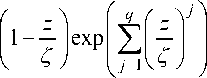
— фак

Пусть q g N, z, Z g C, тогда Aq (z, Z) = тор бесконечного произведения Вейерштрасса порядка q .

Для последовательности комплексных чисел Z = {zk}" |zk| < |zk+1|, к = 1,2,..., |zk| >■< , k >+/ обозначим n (r ) = card {zk: |zk| < r}, 0 < r < +^. При Z = Zf соответствующую считающую функцию назовем nf.

Теорема 1. Пусть 0 < р <+«, 0 < p <+«, р N . Тогда утверждения равносильны:

• 1)    найдется f g H p p ( C ) такая, что Z = { z_k } ”=1 можно представить в виде Z = Z f ;

4^ n^P ( 2 ^k )

• ²⁾    £^ PP T²     ■'. ⁽*)

Доказательство. Согласно свойствам несобственных интегралов сходимость ряда (*) равносильна сходимости интеграла

⁺r n^P ( r )

(**)

—dr < +да .

J _r pp ⁺¹

При 2 ^k <  r <  2 ^{k +1} , n ( 2 ^k ) < n ( r ) < n ( 2 ^{k +1} ) :

7 n p ( r )

J _r pp ⁺¹ 1 '

⁺”² k+ n^p (rA

У [ —Ц dr <

J _r pp ⁺¹

k =0 ₂ k r

+x

< 2

k = 0

( n ( 2 k ^{+ 1} ) ) p

~ n^p ( 2 m )       ±^ n^p ( 2 m )

= 2 p pV

(m-1)pp               mppp m=1 2                m=1 2

.

Поэтому из сходимости (*) вытекает сходимость интеграла (**).

Функция n ( r ) монотонна на R ₊ = [ 0; +да ) . Используя этот факт, несложно показать справедливость обратного утверждения.

Пусть f е H p p ( C ) , Z = Z f . Докажем сходимость интеграла (**).

Применяя неравенство Иенсена, имеем nf (r )< ln M (er, f) + Cf. По- этому

7 n/(r)     ⁺_r" In ^pM(er , f)        7 In ^pM(t , f)

[ dr < [------ dr <  e^pp [------dt < +« .

J    _r pp ⁺¹         J        ^p p p ⁺¹                   J       _fp p ⁺¹

1      '                         1             '                                         e           t

Доказали, что из 1) следует 2). Покажем справедливость обратного ут- верждения.

Пусть q

целое число такое, что q <  p <  q + 1.

+^

E q ^{( z} , z k ) = П A q ^{( z} , z k ) .

k =1

Покажем, что произведение E_q ( z , z_k ) сходится на компактных подмножествах C при E q ( z , z_k ) е H p p ( C ) .

+^     1

Установим, что 2—^+т <+да при q > p -1. Его сходимость эквива- k=1

лентна сходимости

⁺r n(A

[ -yd dt .

J _t q ⁺²

1 t

Пусть 1 < p < +да . Согласно неравенству Гёльдера ясно, что для схо- димости

+f n (t)

dt достаточно обеспечить сходимость

1 tq-

+х

J

dt

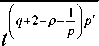
, где

p p =----. Для выполнения условия p -1 < q < +да подберем q е N таким p -1

образом, чтобы выполнялось условие p - 1 <  q <  p .

Докажем, что при выбранных q произведение E_q ( z , z_k ) е H p p ( C ) .

Согласно оценке произведения Вейерштрасса получаем:

ln M ( r , E q ) < K q

r q\ t ^- q ^-1 n ( t ) dt + r q ⁺¹ +[ t ^- q ^-2 n ( t ) dt'

, l ^z l= ^r .

I 1                    r             J

Поэтому

+^

(In М ( r, Eq )) Р r1+P Р

dr <  K ^q

+^

J

J t ^— q ^—1 n ( t ) dt

Vo____________2

¹⁺⁽ p ^— q ) p

+^

dr + f

j t q ² n ( t ) dt

¹⁺ ( p ^— q ^-1 ) p

dr

= K p ( 1 1 + 1 2 ) .

Сходимость интегралов 1 1 , 1 ₂ несложно показать с использованием методов, представленных автором в трудах [5; 6].

Тогда E_q ( z , z k ) е H p p ( C ) (с нулями в точках последовательности

{zk} d.

Пусть 0 <  p <  1. Построим функцию, для которой нулями являются точки последовательности { z k } ”=1 .

Применяя оценку для E_q ( z , z k ) , получим:

r

ln M ( r, E q ) < K q r q J t V 1

—t

+»

■^{q —1} n ( t ) dt + r^{q +1} J t

r

—t

'^{q 2} n ( t ) dt

p

'. ( In M ( r , E ) ) ^q

+^

. 1+ p p

r                      +^

■^q J t ^{— q —1} n ( t ) dt + r^{q +1} J t

1 ______________________ r__

^{1 1+} p p

— I

. .    ^ p q 2 n (t) dt

dr <

< K q

+^ J 1

r

•^q J t ^{— q —1} n ( t ) dt

. 1+ P Р

+^

dr+ J

+^

•^{q +1} J t ^{— q —2} n ( t ) dt

. 1+ PP

dr

= K qp ( 1 1 + 1 2 )

Сходимость 1 1 , 1 ₂ доказывается с применением методов, изложенных в [5; 6].

Из сходимости интегралов     1 1     и    1 ₂     получаем, что

+x

J

( ln M ( r , E q ) ) p

r ¹⁺ p p

dr < +да , при этом p — 1 <  q <  p , p £ N , 0 <  p <+« .

Теорема доказана.

Для целых p имеет место утверждение:

Теорема 2 . Пусть f е H p p ( C ) , p e N . Z = { z k } ”₌₁— последовательность комплексных чисел, | z_k | < | z_{k +1}| , k = 1,2,... , | z_k | ^+« , k ^+да . Тогда следующие условия равносильны:

• 1)    Z = { z_k } ”=1 можно представить в виде Z = Z f для некоторой функции f g A ^p _p ( C ) ;

• 2)    5 _f ( r ) = ^ —— удовлетворяет условиям:

I z_t rz/

*x

J

—---< +w , r

7 ( n ( r ) ) ^p dr

< +”,

J       _r p p ⁺¹              ’

1          '

где n ( r ) — число нулей функции f в круге D_r , 0 <  r < +^ .

При доказательстве данной теоремы используются методы из работ [3; 5]. Необходимость условий из пункта 2) несложно показать с применением неравенства Иенсена.

Доказательство теоремы А.

Покажем, что из пункта 1) следует 2). Предположим, что f g H p p ( C ) ,

{zk}~

—

множество корней

f . Получаем, что по теореме 1:

« n^p ( 2 ^k )

7 —T—- <+да .

3 k pp k=1 2

Из

нее же

следует сходимость произведения

^Eq ( z , z k

.^I z А I 1 ( z

) = П ¹ — ^exp S- —

k = 1 V

z

' k 7

j V z

при p - 1 <  q <  p и его принад-

лежность классу H p p ( C ) .

f ( z )

Тогда g ( z ) = — (     x , z g C , принадлежит H ( C ) , при этом g ( z ) * 0,

^Eq ( z , z_k )

z G C .

Покажем, что g ( z ) = exp ( h ( z ) ) . Причем h ( z ) — полином степени m , m < p . Докажем, что g g H^p p ( C ) .

Согласно равенству ln| g ( z )| = ln| f ( z )| - In| E_q ( z , z_k )|:

1 п                             1 п

2 - J ln ⁺ g ⁽ re - ) \1_Ф <  2 - J ln ⁺ 1 f ⁽ re - ) \1_Ф __ IT                                                      __ TT

- п ln- |a| = max (0, - ln |a|),

С учетом равенства

- п a g C.

п

— J ^ln- | ^Eq ( re '^- , z k ) d - , где

- п

п

2 7 J ^ln| E q ^{( re}'^- , z k - п

п

) d- = 2^ Jln * Eq(

-

- п

п

re ^- , ^zk

^r e^{i p} , ^zk

-п

воспользуемся равенством Иенсена.

• 1    П                                 r n ( t )         1    П

• — J ^ln- | ^E _g ( ^r e“^P , z k ) ^ Ф ⁺ j ""T^ dt ^ — j ^{ln +} | ^Eq ( ^r e“^P , z k ) ^d ^ ^ ^ln

^{2 П} - n ¹                      0 t ^{2 n} - П ¹

Из последних оценок вытекает :

• 1    П

• — J ln ⁺ | g ( re^{1 9} ) d ^ <  C ln M ( r , E_q ) + ln M ( r , f ). - П

Для произвольных 0 <  r <  R получим:

• 1    R + r ⁿ

ln M ( r , g ) < —•---- Jln g ( Re ⁹ ) d 9 .

2n R - r ^{J 1 x}

- П

Пусть R = 2 r , тогда согласно оценке

П

• — J ln ⁺ g ( re ⁹ ) d ^ <  C ln M ( r , E_q ) + ln M ( r , f ) - П

имеем

7 ^{M ( r};g ⁾ > 7 < C

J         _r рр ^{+1                1}

1              '

+х

p

7 ( In M (2 r , E q ) )^ 7 ( In M (2 r , f ) )

. рр +1

. рр +1

p dr

= ^C 2 I

, рр +1

+f ( ln M ( r , f ) ) p

. рр +¹

dlr < +эт .

Т. е. g g H^p_p ( C ) , при этом g ( z ) * 0, z g C .

Тогда g ( z ) = exp ( h ( z ) ) , h ( z ) — целая функция. Пусть u ( z ) = Re h ( z ) , z g C . Не ограничивая общности, примем u ( z ) >  1.

Из того, что функция g принадлежит классу H ^р_р ( C ) , получаем

⁺" ( ln M ( r , u ) ) P

-----3—— dr <+* ,

J        r рр+1                   ’ i              '

где M ( r , u ) = max ( u ,0 ) .

По теореме о среднем и исходя из справедливости предыдущих рассуждений получим:

Я ln M ( r , u )) ;

J        + —^dr <^+да .

i r

Из монотонности функции In M ( r , u ) и сходимости последнего инте

..   M (R, u) _ грала получим, что lim-------= 0.

^{r         J}            R >  - R ^p P

m

Согласно формуле Шварца: h ( z ) = ^ a ^ z ^ , где k < р p . Причем k =0

+^

J

( ln M ( r , h ) ) p

r pp ⁺¹

dr < +«.

Учитывая, что M ( r , h ) ~ | h m | r m , получаем: m < p .

Обратное утверждение очевидно.

Теорема А доказана.

Доказательство теоремы Б несложно провести с использованием теоремы 2.

Заключение

В работе построено факторизационное представление, а также получено описание корневых множеств функций класса H^р_р ( C ) при нецелых неотрицательных значениях порядка p (теорема А) и p e N (теорема Б). Доказательство теорем проведено с использованием методов, приведенных в работах [2–6].