О поверхностных волнах на вязкоупругом цилиндрическом диске

Рассматривается распространение поверхностных волн на вязкоупругом диске. Спектральная задача сводится к решению системы обыкновенных дифференциальных уравнений первого порядка с переменными комплексными коэффициентами. Решение системы дифференциальных уравнений выражается с помощью цилиндрических специальных функций Бесселя и Ханкеля. Частотные уравнения решаются численно методами Мюллера и Гаусса. Исследовано изменение собственной частоты и фазовой скорости в зависимости от волнового числа. Также задача решается численно, методом ортогональной прогонки Годунова и методом Мюллера. Сравниваются полученные численные результаты.

Ключевая слова : собственные колебания; диссипативные свойства; спектральная задача; собственная частота; волновое число.

Одной из центральных задач динамической теории упругости является исследование распространения возмущения напряженно-деформированного состояния в деформируемых телах (с учетом вязкоупругих свойств) с геометрическими структурами [1, 2, 3, 4]. Основными особенностями волновода являются протяженность в одном направлении, а также ограничение и локализация волнового пучка по другим направлениям. Учет демпфирующей способности материала волновода играет огромную роль в динамическом поведении конструкции.

В бесконечной однородной изотропной среде существуют только волны P и S . Однако там, где имеется поверхность, разделяющая среду с различными упругими свойствами, могут распространяться волны. Амплитуды этих волн уменьшаются с удалением от данной поверхности.

Изучение свойств волноводных мод важно также в связи с разработкой методики использования акустической эмиссии для оценки уровня напряженности элементов конструкций [5, 6, 7]. В радиоэлектронной технике широко используются широкие пучки поверхностных волн. Наиболее важным для практики (сейсморазведки) типов поверхностных волн являются рэлеевские волны, распространяющиеся вдоль свободной поверхности твердой среды. Из динамической теории упругости известно [8, 9], что поверхностные волны Рэлея распространяются на полупространстве с прямолинейными границами. Поэтому исследование распространения волн в теле с криволинейными областями является актуальной задачей.

• 1.    Постановка задачи и методы
  
  решения

Рассмотрим распространение поверхностных волн на цилиндрическом теле, находящемся в плоском деформируемом состоянии. Уравнение движения вязкоупругого тела, в цилиндрических координатах (r, θ , z), принимает вид [10, 11]

d ² u

^P ~dt‘ d ² u

P ~dt- где

1 r   z~ ~~aSA 2p d« у = (A + 2p)-------, d r r dO

о ,~ SA     d «

— = ^{( A} + 2 p )- — + 2 p —z -, r dO      d r

_A=d u r + u r + 1 d u p . « = 1 P i + Ц о - 1 d r | d r r r d i z 2 (d r r r d O j

t

A f ( t ) = A f ( t ) - f R ( t - т ) f ( т ) dT ;

_           0

■              t.

^{p f (} t ) = p 0 ^{f (} t ) - I ^R p ⁽ t ^{- т} ) ^{f ( т} ) d^T ,

_0

где f ( t ) - произвольная функция времени; R _A ( t - т ) и R _p ( t - т ) - ядро релаксации; A 0

и µ ₀ – мгновенный модуль упругости; ρ – плотность материала, ~ = const = v ₀ - коэффициент Пуассона.

Внешние нагрузки на свободной цилиндрической поверхности r = R 1 отсутствуют, т.е. e rr =Q т _{г 0} = 0 или

(^err \ = R

~

^{( т} г О ) r = R

E 1 л d u_r I

--A+— r

1 + ~ _ 1 + ~     d r JI

= 0, r = R

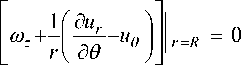
Е – операторный модуль упругости, который имеет вид [12, 13]:

E ~ f ( t ) = E 01

t f (t)-f RE (t - т )f (t)dт

Г ^C ( o r ) = ОТ R a ( т ) coso R тdт , Г (« R ) = f R ^sin ord- 00

соответственно, косинус и синус образы Фурье ядра релаксации материала. После некоторых несложных преобразований ( R _a = R _p = R_e = R 1 ) уравнения движения (1) можно преобразовать к виду:

• ^{d 2 u} r     2 SA 2 _{2 T}««

• —= c Tc 2 T —;

5 1 ^{2     11} 5 r r ²¹ dO      (5)

• £2 ° = c 2 t 1 ^dA + 2 CT « , d t ^{2     11} r d O          d r

где

Т 1 = 1 -Г С ( « R ) - ' T ( « R ).

c l = ( ^ 01 ^{+ 2 p} 0l )/ ^p , c 2 = ^p 0l / P ■

Системы дифференциальных уравнений в частных производных (5) решаются аналитическим путем, т.е. получаются дисперсионные соотношения, содержащие функции Бесселя 1-го рода комплексного аргумента. Дисперсионные соотношения представляются

трансцендентными уравнениями и решаются методом Мюллера. Для этого использованы асимптотические функции Бесселя при малых и больших значениях аргумента.

С помощью соответствующих преобразований [14] системы дифференциальных уравнений (5) могут быть выражены в виде

d A 2_п2 Д d O_z     2v-T-2

—_r = c 2 V ² A , —- = c ₂ V ² « _z ,

S t^{2      1}           d t^{2       2} z

где

_w 2    d ²     1 d 1 d ²

V +1 .

d r ²    r d r   r ² d O²

RE (t - т) - ядро релаксации; E01 - мгновенный модуль упругости.

В центре цилиндрического тела ( r =0) предполагается, что перемещение ограничено. Заменим соотношения (3) и (5) приближенными вида [12]:

^p = P 0 1 ^r P ⁽ ^ r ^)- ' ^r P ⁽ « r ) ] ,

^A = A l^-r f ⁽ ® R ^)- ' ¹ A ⁽ « R ^)] ,

E = Е 01 1 -Г С k) - ' Г « ) ] ,        (4)

где ω _R – действительная константа,

ОТ

^Г E^{C (} « R ) = f ^RE ^{( т} ) ^C0S ® R ^T

ОТ dт, IES (or ) =f Re (т)sinoRтdт

ОТ

Л                                                      ОТ

^Г Р ( ® R ) = f ^R p ^{( т} ) ^cos « R ^T d ^T , f p ^S ( o r ) = f R p ( т ) sin «т ат

Частное решение уравнения (6) ищем в виде

«. = w ( r ) e ^{- n O} ) , a = и _A ( r ) e ⁽ « t ^{- n O} ) .(7)

Здесь W , U _A - есть амплитудная комплексная функция, зависящая только от r. Волновое число и фазовая скорость выражаются следующими формулами:

2 π     ωλ

X = —R ; с =--- , где х - волновое чис-

λ     2π ло, с – фазовая скорость распространения волн.

Для выяснения их физического смысла рассмотрим два случая:

• 1)    X = X R ; « = « R + '« (или с = с r +ic I ), тогда решение (7) имеет вид синусоиды по х , амплитуда которой затухает по времени;

  ²⁾ X = X r + iX i ; ^ф = а (или с = с R ) тогда в каждой точке х колебания установившиеся, но по х затухают.

  Подставляя (7) в (6) переходим к уравнениям Бесселя следующего вида:

  
  

  d 2 U л ( r ) + 1 dU ( r ) + dr ²     r dr

  
  

  Ф 12т к с Т

  
  

  —

  
  

  И² Л

  - U л ( r ) = 0 .(8) ^r 7

  
  

  В центре диска ( r =0) предполагается, что перемещение ограничено. С помощью этого условия можно найти выражение В , где В=0. Тогда решение примет вид:

  (9=

  
  

  Решение уравнения (8) выражается через цилиндрические функции Бесселя 1-го и 2-го рода n -го порядка:

  
  

  да

  E

  n = 1

  
  

  г

  
  

  A_nJ_n

  
  

  да

  
  
  
  
  
  
  
  

  к

  
  

  D n H n

  
  

  ф

  r 7

  [ Ф

  r

  к c 1 Т 1

  
  

  л

  
  
  
  

  i ( a t — n d ).

  e

  
  

  и Л ( r ) = E A n J n ф r + B n Y n ф r  ,(9)

  
  

  n = 1 к

  
  

  к сТ 1

  
  
  
  

  cТ

  
  

  При этом перемещение цилиндрическо-

  
  

  где J _n , Y _n – функции Бесселя 1-го и 2-го рода n -го порядка.

  
  

  го

  
  

  тела с учетом

  
  

  дующий вид:

  
  

  (5) и (10) принимает сле-

  
  

  u r =

  
  
  
  

  да

  = E

  n = 0

  
  

  —

  
  

  A n

  
  

  2 c ₁ Т ₁

  ω ²

  
  

  a д J -—r

  
  

  n

  
  

  л

  
  
  
  

  к ^С1 Т 1 7

  
  

  д r

  
  

  2 c ₂ Т ₁ np r ω ²

  
  
  
  

  Ф

  к ^С 2 Т 1

  
  

  к

  
  

  r

  
  

  ei ( a t — n 9 );

  
  
  
  

  к

  u e =

  
  
  
  
  
  

  да

  
  

  = E A

  
  

  n = 0

  
  

  к

  
  

  ² c ₁ Т _{1 J}

  ⁿ 2 ω ^{2 n}

  
  
  
  

  a

  ----r

  
  

  к c^T 1 7

  
  

  —

  
  

  e 2_T ^д Jn c ₂ Т ₁

  n 2

  ω ²

  
  

  Следовательно, для (4) получим совокупность двух граничных условий, которые

  
  

  A n J n (xX ) [ o,5( с / СТ)

  l         ^С2^T 1

  
  

  _—

  
  
  
  

  ^a

  ^r

  к ^С 2 Т 1 7

  д r

  
  

  /

  
  

  e i ^{a —} n e ) .

  
  
  
  
  
  

  приводят к двум однородным уравнениям с двумя неизвестными А _n и D _n :

  
  

  1 + 1/ x ]- nidcbl ^χ

  
  

  С

  J n + 1⁽ xn— O' ^С 2^Т1

  
  

  + i 2 D_n J(x-c- ) n ²(— — 1) +    J _{+ 1}( X^ )k0,

  
  

  С 2 Т L

  
  

  ^χ

  
  
  
  

  c 2 Т 1

  
  

  с 2 Т

  
  

  . ,    1 _r z С , n С _T , С .

  iA 1 ^{1 J}n (ХП   ) —— J n + 1⁽ xn— n+

  ^С2^Т1 ^С 2 Т 1          ^С2^Т1

  
  
  
  

  ^χ

  
  

  + 2 D n 1 [0.5( С / С 2 Т) — 1 + 1/ хП²J n (X— ) - П- J n „( х — ) [ = 0,

  l                                ^С 2 Т 1    ^С 2 Т 1 Х        ^С 2 Т 1

  
  

  где n = с 2 / С 1 .

  
  

  Для того чтобы такая система уравне- литель коэффициентов должен быть равен ний имела нетривиальные решения, опреде- нулю.

  
  

Последнее условие дает зависимость частот волнового числа. Уравнение дисперсии имеет (ω R ) и коэффициентов демпфирования (ω I ) от вид:

—

¹ 1 -c- I 2 1 c ₂T i J

—

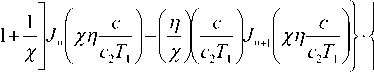
¹ 1 ^ I 2 1 c ₂T i J

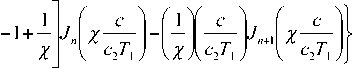
= 0.

Если известно, что n =0 и 1, тогда можно вычислить функции Бесселя и Неймана любого порядка из следующих рекуррентных соотношений (F n =J n ;Y n ):

Fn+1( z) = — Fn (z) — Fn—i( z), z где z – комплексная величина. Комплексное число

2 k

IP I 2      2

• V 0 ⁽ P ^, P ⁾ = E ^(—^ Ъ^Т Sin2 ^kP = ^U 0 ⁽ P ^, P ⁾- (¹⁴) к =o        ^{( k !)}

z = x+iy можно представить в виде z = регф; p = x2 + y2, p = arctg —. x

Из соотношения получим:

.       ( P ’² 2

J o ( p^ ^{г ф} ) = X ( — 1) * -2-r e 2 * ’ = UP ) + iV o ( p , p );

k = 0         ^{( k !)}

2 k

I P I

^U 0 ⁽ P , P ) = X ^{( — 1)} * 77KF ^{cos2 k} P = ^U 0 ⁽ P , p).

k = o         ^{( k !})

Некоторые значения функции Бесселя в зависимости от аргумента ( ф = 10 ° )

z	J 0 (z)		Y 0 ( z )
0,0	0,99041	-0,00021	-1,97937	0,11159
0,1	0,99765	-0,00085	-1,53476	0,11269
0,2	0,99062	-0,00340	-1,08176	0,11597
0,3	0,97895	-0,00761`	-0,80837	0,11999

Для рядов (14) остаток не превосходит первого отброшенного члена. Если выбрать для U 0 (ρ, ф) и V 0 (ρ, ф) по 26 членов рядов (многочлены 50-й степени по р ), то ошибка по р 52     1

модулю будет меньше 1 041 — I ----- мак

1 2 J ( 26! ) 2

симальная величина которой (для ρ <10) приблизительно равна 1,5 10 ^-17. . Результаты вычисления приведены в таблице.

В качестве ядра релаксации вязкоупругого материала примем трехпара-Ae—et метрическое ядро R(t) = —1^а~ Ржаницина-

Колтунова [7], обладающее слабой сингулярностью, где A , α , β – параметры материала [7]. Примем следующие параметры: A = 0,048; в = 0,05; а = 0,1 .

Трансцендентное уравнение (13) решается методом Мюллера. Одновременно мы определили два корня (13) ( v = 0,3 ; х = 100 ) с ⁽¹⁾(100) = 0,919 с ₂, с ⁽²⁾ (100) = 1,032 с ₂.

Из источников [4, 5, 6] известно, что при % = 98 получим c ⁽¹⁾ =0,92c₂, а скорость волны Рэлея с R =0,9194с 2 .

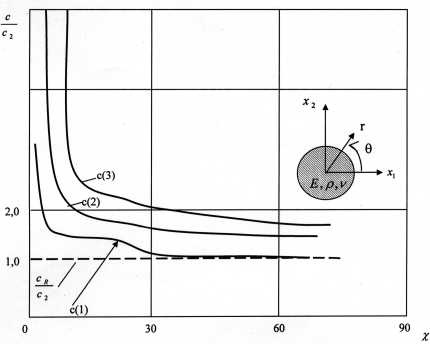
Рис. 1. Зависимость реальной части

Фаз1вой скорости от волнового числа

Результаты расчетов представлены на рис. 1. Отметим характерные особенности кривой 1: фазовая скорость стремится к бесконечности, когда волновое число равно нулю. А при стремлении волнового числа к бесконечности, волновое число стремится к скорости волны Релея для полупространства.

Первая и вторая мода при стремлении волнового числа к нулю имеют частоту отсечки, т.е. фазовая скорость стремится к бесконечности. При больших волновых числах предельная фазовая скорость этой моды совпадает со скоростью волны Релея. На частоте отсечки радиальные перемещения равны нулю и цилиндр находится в статическом плоском деформированном состоянии. У второй моды на частоте отсечки наблюдаются только реальные части, а мнимые части принимают конечные значения при стремлении волнового числа к нулю. В отличие от известных, в этом случае кроме скорости волны Рэлея при больших волновых числах С _R ⁽¹⁾ существует счетное множество мнимых скоростей (рис. 1).

На поверхности полости также распространяются волны Рэлея, но комплексные (рис. 2).

A =

D n

—

2in²J(xz ) -^{— 1}

I       L x   .

+ J n + 1 ⁽xz )

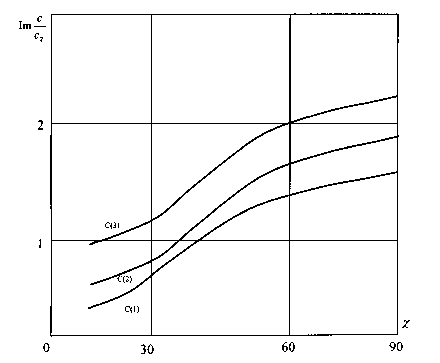
Рис. 2. Зависимость мнимой части фазовой скорости от волнового числа

J ⁽xnz )

0.5 z ^{2 — 1} + - ^{— П} J + 1 ⁽%ф ) X J X

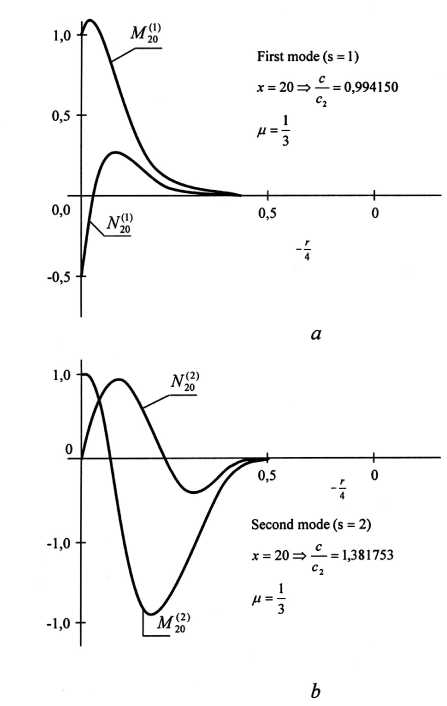
Рис. 3. Формы колебаний соответствующих первых (а) и вторых (b) фазовых скоростей

Если использовать (11), (12) и (15), тогда получим следующие величины перемещения:

ur

D n R 1

2π

z

rR

^— n ^Jn + 1 ⁽ xn ^z —) ⁺ — ^J„

R ₁ zr

⁽ xn z-r- ) L

R

n

—

R T r A ----^J n ⁽ Xz ^-) f ^e χzr R

u _θ

D n R 1

21

z

R               r 1             r

— Ln ^J n ⁽ ХП ^z —) ⁺ —^J n + 1 ⁽ X^z —)

Rχ

zr

R

—

R^ т _t^r A ----^J n ⁽ X z —) f ^e

Xzr        ^R 1

i ( at — nB )

,

i ⁽'' " ^— n ^e > , (16)

где z = c / c 2 Т1,

Обобщая выражения (16), будем иметь

^Jn ⁽ Xz )--^{1 +} J n + 1 ⁽ Xz )

L n

χ

x ^J„ ⁽ xnz ) 2 z²

—

¹ + 1 ^χ

—

.

nz ^J„ + 1 ⁽ xnz )

ur

D n R 1 u _θ

_r = Ampl ( u r ) e i^{( м — п в} + ^{n /2)},

D n R 1

_r = Ampl ( u _B ) e i^{( a t — n B} + ^{n /2)}.

Амплитуды перемещений представим в виде

L n

rR    r

^— nJ n + 1 ⁽ xnz —) + — J n ⁽ xnz —)

R ₁ zr           R ₁

—

r

J_n ( χz   )

R ₁

( s )     Ampl ( u_r )

M „ = —--—-- -

n

Ampl ( u _r )

ur

⁽ ur ) r - R

L n

—

nJ n + 1 ⁽ xnz ) + ¹ J _n ⁽ xnz ) z

—

r χz_{R 1} J_n ( χz ) χz

,

N s ) -

Ampl ( u _θ )

Ampl ( u _r )

L n

J n ( xnz^ ) J n + 1 ( xz r )

_________ R 1 ₊_________ R 1

zr            χ

R 1

—

r

J_n ( χz   )

R ₁

r ηz R 1

L n

—

nJ n + 1 ⁽ xnz ) + ¹ J _n ⁽ xnz ) z

—

J_n ( χz ) χz

Численные расчеты проведены при v - 0,33, n - 1/43 . Результаты расчетов амплитуды перемещений представлены на рис. 3 (a, b). Из рисунков видно, что движения локализованы на поверхности цилиндра.

• 1.    Установлено, что существует бесконечное множество корней трансцендентного уравнения (13), где первый корень при больших значениях стремится к скорости волны Рэлея С =0,92с 2 . Фазовая скорость стремится к бесконечности, когда волновое число равно нулю, т.е. имеет место частота осечки.

• 2.    Выявлено, что движения цилиндрического диска локализуются на поверхности цилиндра.

• 3.    Учет вязких свойств материала уменьшает значения фазовых скоростей на 10–15 %.

• 1.    Уайт. Поверхностные упругие волны / Тр. Ин-та инженеров по электротехнике и радиоэлектронике. 1970, 58, № 8. С. 68–110.

• 2.    Ewing W.M., Jardetzku W.S., Press F. Elastic Waves in Layered Media, McGraw – Hill, New York, 1962.

• 3.    Дейвис Р.М. Волны напряжений в твердых телах. М.: Изд-во иностр. лит-ры, 1961. 104 с.

• 4.    Сафаров И.И. Колебания и волны в диссипативно недородных средах и конструкциях Ташкент: Фан, 1992. 250 с.

• 5.    Сафаров И.И., Ахмедов М.Ш., Болтаев З.И. Колебания и дифракция волн на цилиндрическом теле в вязкоупругой среде. Lambert Academic Publishing (Germany). 2016. 262 р.

• 6.    Сафаров И.И., Тешаев М.Х., Болтаев З.И. Волновые процессы в механическом волноводе. LAP, LAMBERT Academic publishing. Германия. 2012. 217 с.

• 7.    Колтунов М.А. Ползучесть и релаксация. М.: Высшая школа, 1976. 277 с.

• 8.    Колтунов М.А., Майборода В.П., Зубчани-нов В.Г. Прочностные расчеты изделий из полимерных материалов. М: Машиностроения, 1983. 239 с.

• 9.    Болотин В.В., Новичков Ю.Н. Механика многослойных конструкций. М.: Машиностроение, 1980. 375 с.

• 10 .    Базаров М.Б., Сафаров И.И., Шокин Ю.М. Численное моделирование колебаний диссипативно-неоднородных и однородных механических систем. Новосибирск, Сибирское отделение РАН, 1996. 189 с.

• 11.    Каюмов С.С., Сафаров И.И. Распространение и дифракция волн в диссипативнонеоднородных цилиндрических деформируемых механических системах. Ташкент: Фан, 2004. 215 с.

• 12.    Сафаров И.И., Ахмедов М.Ш., Болтаев З.И. Собственные волны в слоистых средах. Lambert Academic Publishing (Germany). 2016. 192 с.

• 13.    Гринченко В.Т., Малешко В.В. Гармонические колебания и волны в упругих телах. Киев: Наукова думка, 1981. 283 с.

• 14 .    SafarovI.I., Boltaev Z.I., Akhmedov M.Sh. Properties of wave motion in a fluid-filled cylindrical shell. LAP, Lambert Academic Publishing. 2016. 105 р.

• 15.    Safarov I.I., Akhmedov M.Sh., Boltaev Z.I. Natural oscillations and diffraction of waves on the cylindrical body. Lambert Academic Publishing (Germany). 2016. 245 р.

On surface waves on a viscoelastic cylindrical disk